1.4 עקרון אי הוודאות

גלים מטושטשים

כפי שהראינו עבור מנות גל, אופי הגל של החלקיקים מרמז שאיננו יכולים לדעת הן את המיקום והן את המומנטום של חלקיק במידה שרירותית של דיוק - אם \(\Delta x\) מייצג את חוסר הוודאות בידע שלנו על המיקום, \(\Delta p\) וזה של המומנטום, אז

\[ \Delta p \Delta x \sim h \tag{1.4.1} \]

\(h\)איפה הקבוע של פלאנק. בעולם האמיתי, חלקיקים הם תלת מימדיים ועלינו לומר \[ \Delta p_x \Delta x \sim h \tag{1.4.2} \]

עם משוואות מתאימות לשני הכיוונים המרחביים האחרים. הערפול לגבי המיקום קשור לזה של המומנטום באותו כיוון.

בואו נראה איך זה עובד על ידי ניסיון למדוד y -position ו- y -momentum בצורה מדויקת מאוד. נניח שיש לנו מקור לאלקטרונים, נניח, אקדח אלקטרונים ב- CRT (צינור קרן קתודה, כגון צג מיושן). הקורה מתפשטת מעט, אך אם אנו מניחים יריעת מתכת עם חריץ רוחב\(w\), אז לחלקיקים שעוברים אותה דרך החריץ, אנו יודעים \(y\) באי וודאות\(\Delta y=w\). כעת, אם החריץ נמצא דרך ארוכה במורד הזרם ממקור אקדח האלקטרונים, אנו גם יודעים בצורה מדויקת \(p_y\) מאוד כאשר האלקטרון מגיע לחריץ, מכיוון שכדי להגיע לחריץ מהירות האלקטרון תצטרך להיות מכוונת בדיוק כמו שצריך.

אך האם מדידת מיקום ה- y של האלקטרון - במילים אחרות, אם הוא עובר דרך החריץ - משפיעה על המומנטום y שלו? התשובה היא כן. אם זה לא קרה, אז שליחת זרם של חלקיקים דרך החריץ כולם היו פוגעים קרוב מאוד לאותה נקודה על מסך המוצב במורד הזרם. אבל אנחנו יודעים מניסוי שזה לא מה שקורה - דפוס עקיפה של חריץ בודד מצטבר, ברוחב זוויתי\(\theta \sim \lambda/w\), שבו אורך הגל \(\lambda\) של האלקטרון דה ברוגלי ניתן על ידי \(p_x \cong h/\lambda\) (יש תרומה זניחה מ- y -מומנטום). \(\lambda\) אי הוודאות הנובעת מכך היא \(p_y\)

\[ \Delta p_y/p_x \sim \theta \sim \lambda/w \tag{1.4.3} \]

מכניסים פנימה\(p_x = h/\lambda\), אנו מוצאים מיד את זה

\[ \Delta p_y \sim h/w \tag{1.4.4} \]

כך שפעולת מדידת מיקום y של האלקטרון טשטשה את המומנטום y שלו בדיוק בכמות הנדרשת על ידי עקרון אי הוודאות.

מנסה לנצח את עקרון אי הוודאות

על מנת להבין טוב יותר את עקרון אי הוודאות, בואו ננסה לראות מה משתבש כאשר אנו מנסים למדוד מיקום ומומנטום בצורה מדויקת יותר מהמותר.

לדוגמה, נניח שאנו מסתכלים על אלקטרון דרך מיקרוסקופ. מה יכולנו לצפות לראות? כמובן, אתה יודע שאם ננסה להסתכל על משהו ממש קטן דרך מיקרוסקופ הוא מטשטש - אובייקט קטן וחד מקבל דפוסי עקיפה סביב קצוותיו, מה שמעיד על כך שאנו מסתכלים על משהו בגודל השווה לאורך הגל של האור בשימוש. אם נסתכל על משהו קטן בהרבה מאורך הגל של האור - כמו האלקטרון - היינו מצפים לדפוס עקיפה של טבעות קונצנטריות עם כתם עגול באמצע. גודל התבנית הוא בסדר אורך הגל של האור, למעשה מאופטיקה ניתן להראות \(\sim\lambda f/d\) היכן \(d\) נמצא קוטר עדשת האובייקט של המיקרוסקופ, מרחק \(f\) המוקד (המרחק מהעדשה לאובייקט). אנחנו ניקח\(f /d \sim 1\), כפי שהוא בדרך כלל. אז התבוננות באובייקט בגודל של אלקטרון אמורה לתת דפוס עקיפה שבמרכזו מיקום האובייקט. נראה שזה מצמיד את עמדתו בצורה מדויקת למדי.

מה לגבי המומנטום של האלקטרון? כאן מתעוררת בעיה שלא משנה לאובייקטים גדולים יותר - האור שאנו רואים הקפיץ, כמובן, מהאלקטרון, ולכן לאלקטרון יש תנופת רתיעה כלשהי. כלומר, על ידי הקפצת אור מהאלקטרון נתנו לו תנופה מסוימת. אפשר לומר כמה? כדי לעשות את זה פשוט, נניח שיש לנו עיניים טובות ורק צריך להקפיץ פוטון אחד מהאלקטרון כדי לראות אותו. אנו מכירים את המומנטום הראשוני של הפוטון (מכיוון שאנו יודעים את כיוון קרן האור בה אנו משתמשים כדי להאיר את האלקטרון) ואנחנו יודעים שאחרי הקפצה, הפוטון פוגע בעדשת האובייקט ועובר דרך המיקרוסקופ, אך אנו לא יודע היכן הפוטון פגע בעדשת האובייקט. כל העניין במיקרוסקופ הוא שכל האור מנקודה, אור שפוגע בעדשת האובייקט במקומות שונים, ממוקד כולו בחזרה לנקודה אחת ויוצר את התמונה (מלבד הטשטוש שהוזכר לעיל). אז אם לאור יש אורך גל\(\lambda\), לפוטונים המרכיבים אותו יש מומנטום\(\sim h/\lambda\), ומתוך בורותנו היכן נכנס הפוטון למיקרוסקופ איננו בטוחים במומנטום הכיוון x שלו בכמות\(\sim h/\lambda\). בהכרח, אם כן, יש לנו את אותה אי וודאות לגבי תנופת כיוון ה - x של האלקטרון, מכיוון שהדבר הועבר על ידי הפוטון שקפץ.

אבל עכשיו יש לנו בעיה. בניסיונותינו למזער את חוסר הוודאות במומנטום של האלקטרון, על ידי שימוש בפוטון אחד בלבד כדי לזהות אותו, לא נראה הרבה מדפוס העקיפה שנדון לעיל - דפוסי עקיפה כאלה נוצרים על ידי פוטונים רבים הפוגעים בסרט, ברשתית או בכל דבר אחר. ציוד גילוי נמצא בשימוש. פוטון בודד מייצר נקודה אחת (במקרה הטוב!). סביר להניח שנקודה זו תהיה בסדר \(\lambda\) של מרכז התבנית, אך הדבר מותיר אותנו עם אי וודאות במיקום הסדר \(\lambda\).

לכן, בניסיון להתבונן במיקום ובמומנטום של אלקטרון בודד באמצעות פוטון בודד, אנו מוצאים אי וודאות במיקום \(\Delta x\sim\lambda\) ובמומנטום\(\Delta p_x\sim h/\lambda\). תוצאות אלו תואמות את עקרון אי הוודאות של הייזנברג. \(\Delta x\Delta p_x\sim h\)

כמובן, נוכל להצמיד את המיקום הרבה יותר טוב אם היינו משתמשים \(N\) בפוטונים במקום באחד. מן התיאוריה הסטטיסטית, ידוע כי אי הוודאות שנותרה\(\sim \lambda/\sqrt{N}\). אבל אז \(N\) פוטונים קפצו מהאלקטרון, ולכן מכיוון שכל אחד מהם סביר באותה מידה לעבור כל חלק בעדשת האובייקט, המומנטום הבלתי בטוח של האלקטרון כתוצאה מהתנגשויות אלה עולה כמו. \(\sqrt{N}\) (זהה לחוסר האיזון הממוצע בין ראשים וזנבות ברצף של הטלות \(N\) מטבעות.)

מציין כי חוסר הוודאות במומנטום של האלקטרון מתעורר מכיוון שאיננו יודעים היכן עובר הפוטון המוקפץ דרך עדשת האובייקט, מפתה לחשוב שנוכל פשוט להשתמש בעדשת אובייקט קטנה יותר, שתפחית. \(\Delta p_x\) למרות שזה נכון, זכור מלמעלה כי קבענו שגודל דפוס העקיפה היה\(\sim \lambda f/d\), \(d\) היכן קוטר עדשת האובייקט ואורך המוקד \(f\) שלה. קל לראות שדפוס העקיפה, וכתוצאה מכך\(\Delta x\), הולך וגדל רק בכמות \(\Delta p_x\) שהולכת וקטנה!

צפייה באלקטרונים בניסוי החריץ הכפול

נניח כעת שבניסוי החריץ הכפול, יצאנו לזהות איזה חריץ עובר כל אלקטרון על ידי הארת אור ממש מאחורי המסך וצפייה באור מוחזר מהאלקטרון מיד לאחר שעבר דרך חריץ. בעקבות הדיון בהרצאות פיינמן בפיזיקה, כרך ג ', נקבע כעת שאם נוכל לזהות את האלקטרונים, אנו הורסים את דפוס העקיפה!

אם לוקחים את המרחק בין שני החריצים\(d\), הקווים הכהים בתבנית העקיפה נמצאים בזוויות \[ (n+\frac{1}{2})\lambda_{elec}=d\sin\theta \tag{1.4.5} \]

אם האור המשמש לראות איזה חריץ האלקטרון עובר מייצר אי וודאות במומנטום y של האלקטרון \(\Delta p_y\) 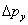, כדי לא להרוס את דפוס העקיפה עלינו להיות \[ \Delta p_y/p <\lambda_{elec}/d \tag{1.4.6} \]

(אי הוודאות הזוויתית בכיוון האלקטרון לא יכולה להספיק כדי להפיץ אותו מתבנית העקיפה מקסימום למינימום). \(p\)הנה המומנטום המלא של האלקטרון,\(p=h/\lambda_{elec}\). כעת, חוסר הוודאות במומנטום y של האלקטרון, מחפש אותו במיקרוסקופ, הוא\(\Delta p_y \sim h/\lambda_{light}\).

החלפת ערכים אלה באי-השוויון שלמעלה אנו מוצאים שהתנאי לדפוס העקיפה לשרוד הוא \[ \lambda_{light}>d \tag{1.4.7} \]

אורך הגל של האור המשמש לזיהוי איזה חריץ עבר האלקטרון חייב להיות גדול מהמרחק בין החריצים. למרבה הצער, האור המפוזר מהאלקטרון נותן נקודה אחת בתבנית עקיפה בגודל אורך הגל של האור המשמש, כך שגם אם אנו רואים את ההבזק זה לא מצמיד את האלקטרון מספיק כדי לומר איזה חריץ הוא עבר. הייזנברג מנצח שוב.

כיצד עקרון אי הוודאות קובע את גודל הכל

מעניין לראות כיצד הגודל הפיזי האמיתי של אטום המימן נקבע על פי אופי הגל של האלקטרון, למעשה, על ידי עקרון אי הוודאות. במצב הקרקע של אטום המימן, האלקטרון ממזער את האנרגיה הכוללת שלו. עבור אטום קלאסי, האנרגיה תהיה מינוס אינסוף, בהנחה שהגרעין הוא נקודה (וגדולה מאוד בכל מקרה) מכיוון שהאלקטרון ישב ממש על גבי הגרעין. עם זאת, זה לא יכול לקרות במכניקת הקוונטים. לאלקטרון מאוד מקומי כזה תהיה אי וודאות גדולה מאוד במומנטום - במילים אחרות, האנרגיה הקינטית תהיה גדולה. זה נראה בצורה הברורה ביותר על ידי דמיון שהאלקטרון הולך במסלול מעגלי של רדיוס \(r\)עם תנע זוויתי\(h/2p\). ואז אורך גל אחד של גל דה ברוגלי של האלקטרון פשוט מתאים סביב המעגל,. \(\lambda_{elec}=2\pi r\) ברור שכאשר אנו מכווצים את רדיוס המעגל\(r\), \(\lambda_{elec}\) יורד באופן יחסי, והמומנטום של האלקטרונים

\[ p=h/\lambda_{elec}=h/2\pi r \tag{1.4.8} \]

מגביר. הוספת האנרגיה הפוטנציאלית האלקטרוסטטית של האלקטרון אנו מוצאים שהאנרגיה הכוללת למסלול רדיוס מעגלי \(r\) היא:

\[ E(r)=K.E.+P.E.=\frac{p^2}{2m}-\frac{e^2}{4\pi \varepsilon_0r}=\frac{h^2}{8m\pi^2r^2}-\frac{e^2}{4\pi\varepsilon_0r} \tag{1.4.9} \]

שימו לב שעבור גדול \(r\) מאוד האנרגיה הפוטנציאלית שולטת, האנרגיה הקינטית זניחה, וכיווץ האטום מוריד את האנרגיה הכוללת. עם זאת, עבור קטן מספיק\(r\), מונח האנרגיה הקינטית (החיובי תמיד) מנצח, והאנרגיה הכוללת גדלה ככל שהאטום מתכווץ. ברור, אם כן, חייב להיות ערך \(r\) שעבורו האנרגיה הכוללת היא מינימום. הדמיית גרף של האנרגיה הכוללת שניתנה על ידי המשוואה לעיל כפונקציה של\(r\), בנקודת המינימום השיפוע של \(E(r)\) הוא אפס,\(dE(r)/dr=0\).

כלומר,

\[ -\frac{h^2}{4m\pi^2r}+\frac{e^2}{4\pi \varepsilon_0}=0 \tag{1.4.10} \]

נתינה

\[ r_{min}=\frac{\varepsilon_0h^2}{\pi me^2} \tag{1.4.11} \]

האנרגיה הכוללת לרדיוס זה היא התשובה הנכונה המדויקת, שהיא מרגיעה (אך לא מגיע לנו, מכיוון שהשתמשנו בתמונה נאיבית, כפי שיתברר בהמשך.)

המטרה של תרגיל זה היא לראות שבמכניקת הקוונטים, בניגוד למכניקה הקלאסית, חלקיק אינו יכול למקם את עצמו במינימום המדויק של אנרגיה פוטנציאלית, מכיוון שזה ידרוש חבילת גל צרה מאוד ובכך יהיה יקר באנרגיה קינטית. מצב הקרקע של חלקיק קוונטי בפוטנציאל אטרקטיבי הוא החלפה בין מזעור אנרגיה פוטנציאלי למזעור אנרגיה קינטית. כך הגדלים הפיזיים של אטומים, מולקולות ובסופו של דבר עצמנו נקבעים על ידי הקבוע של פלאנק.

תורם

• Template:ContribFowler