ב: יסודות מתמטיים
- Page ID
- 208931
ריבועים וכוחות אחרים
אקספקטנט, או כוח, הוא קיצור מתמטי לכפולות חוזרות ונשנות. לדוגמה, המעריך "2" פירושו להכפיל את הבסיס לאותו מעריך בפני עצמו (בדוגמה כאן, הבסיס הוא "5"):
\[5^2=5×5=25\]
המעריך הוא "2" והבסיס הוא המספר "5". ביטוי זה (הכפלת מספר בפני עצמו) נקרא גם ריבוע. כל מספר שהועלה לעוצמה של 2 נמצא בריבוע. כל מספר שהועלה לכוח של 3 נמצא בקוביות:
\[5^3=5×5×5=125\]
מספר שהועלה לכוח הרביעי שווה למספר זה כפול בעצמו ארבע פעמים, וכן הלאה עבור כוחות עליונים. באופן כללי:
\[n^x=n×n^{x−1}\]
חישוב אחוזים
אחוז הוא דרך לבטא כמות חלקית של משהו באמצעות שלם המחולק ל 100 חלקים. אחוז הוא יחס שהמכנה שלו הוא 100. אנו משתמשים בסמל האחוזים,%, כדי להראות אחוזים. לפיכך, 25% פירושו יחס של\(\frac{25}{100}\), 3% פירושו יחס של\(\frac{3}{100}\), ו 100% אחוז פירושו\(\frac{100}{100}\), או שלם.
המרת אחוזים
ניתן להמיר אחוז לשבר על ידי כתיבת ערך האחוז כשבר עם מכנה של 100 ופישוט השבר במידת האפשר.
\[25\%=\dfrac{25}{100}=\dfrac{1}{4}\]
ניתן להמיר אחוז לעשרוני על ידי כתיבת ערך האחוז כשבר עם מכנה של 100 וחלוקת המונה במכנה.
\[10\%=\dfrac{10}{100}=0.10\]
כדי להמיר עשרוני לאחוז, כתוב את העשרוני כשבר. אם המכנה של השבר אינו 100, המירו אותו לשבר עם מכנה של 100 ואז כתבו את השבר כאחוז.
\[0.833=\dfrac{833}{1000}=\dfrac{83.3}{100}=83.3\%\]
כדי להמיר שבר לאחוז, המירו תחילה את השבר לעשרוני ואז המירו את העשרוני לאחוז.
\[\dfrac{3}{4}=0.75=\dfrac{75}{100}=75\%\]
נניח שחוקר מגלה ש -15 מתוך 23 תלמידים בכיתה הם נשאים של Neisseria meningitides. איזה אחוז מהתלמידים הם נשאים? כדי למצוא ערך זה, הביע תחילה את המספרים כשבר.
\[\mathrm{\dfrac{carriers}{total\: students}}=\dfrac{15}{23}\]
ואז לחלק את המונה על ידי המכנה.
\[\dfrac{15}{23}=15\div 23 \approx 0.65\]
לבסוף, כדי להמיר עשרוני לאחוז, הכפל ב 100.
\[0.65 \times 100=65\%\]
אחוז הסטודנטים שהם נשאים הוא 65%.
אתה עשוי גם לקבל נתונים על התרחשות ואי התרחשות; לדוגמה, במדגם של תלמידים, 9 נבדקו חיוביים לנוגדני Toxoplasma, בעוד 28 נבדקו שליליים. מה אחוז התלמידים הסרופוזיטיביים? הצעד הראשון הוא לקבוע את ה"שלם ", שהתלמידים החיוביים הם חלק ממנו. כדי לעשות זאת, לסכם את הבדיקות החיוביות ושליליות.
\[\mathrm{positive+negative=9+28=37}\]
כל המדגם כלל 37 תלמידים. החלק החיובי הוא:
\[\mathrm{\dfrac{positive}{total\: students}=\dfrac{9}{37}}\]
כדי למצוא את אחוז התלמידים שהם נשאים, חלק את המונה במכנה והכפיל ב 100.
\ [\ dfrac {9} {37} =9\ דיב 37\ בערך 0.24\\ 0.24\ פעמים 100 = 24\
%\]
אחוז התלמידים החיוביים הוא כ -24%.
דרך נוספת לחשוב על חישוב אחוזים היא להגדיר שברים שווים, שאחד מהם הוא שבר עם 100 כמכנה, והכפלה צולבת. הדוגמה הקודמת תתבטא כ:
\[\dfrac{9}{37}=\dfrac{x}{100}\]
עכשיו, לחצות להכפיל ולפתור עבור הלא נודע:
\ [\ התחל {יישור}
9\ פעמים 100 &=37 x &\ n מספר בודד\\ [5pt]\ frac {9
\ פעמים 100} {37} &=x &\ טקסט {חלק את שני הצדדים ב 37}\\ n מספר בודד\\ [5pt]\ frac {900} {37} &=x & &
\ טקסט {הכפל}\nמספר\\ [5 נק]
24 &\ בערך x &\ טקסט {חלוקה}\ n מספר יחיד\ סוף {יישור}\]
התשובה, מעוגלת, זהה.
הכפלה וחלוקה בעשרות
בתחומים רבים, בעיקר במדעים, מקובל להכפיל עשרונים בכוחות של 10. בואו נראה מה קורה כשאנחנו מכפילים את 1.9436 בכמה כוחות של 10.
\ [\ התחל {יישר}
1.9436 (10) & =19.436\ n מספר בודד\\ 1.9436 (100) &=194.36\ n מספר בודד\\
1.9436 (1000) &=1943.6\ n מספר אחרון\ סוף {יישור}\]
מספר המקומות שהנקודה העשרונית נעה זהה למספר האפסים בעוצמה של עשרה. הטבלה \(\PageIndex{1}\) מסכמת את התוצאות.
| הכפל על ידי | אפסים | נקודה עשרונית נעה. |
|---|---|---|
| 10 | 1 | 1 מקום מימין |
| 100 | 2 | 2 מקומות מימין |
| 1,000 | 3 | 3 מקומות מימין |
| 10,000 | 4 | 4 מקומות מימין |
אנו יכולים להשתמש בתבנית זו כקיצור דרך להכפלה בכוחות של עשרה במקום להכפיל באמצעות הפורמט האנכי. אנו יכולים לספור את האפסים בעוצמה של 10 ואז להזיז את הנקודה העשרונית באותו מספר מקומות ימינה.
אז, למשל, כדי להכפיל 45.86 על ידי 100, להזיז את הנקודה העשרונית 2 מקומות ימינה.
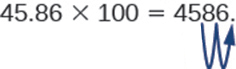
לפעמים כשאנחנו צריכים להזיז את הנקודה העשרונית, אין מספיק מקומות עשרוניים. במקרה כזה, אנו משתמשים באפסים כמצייני מיקום. לדוגמה, בואו נכפיל 2.4 ב 100. אנחנו צריכים להזיז את הנקודה העשרונית 2 מקומות ימינה. מכיוון שיש רק ספרה אחת מימין לנקודה העשרונית, עלינו לכתוב 0 במקום המאות.
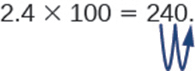
כאשר מחלקים על ידי כוחות של 10, פשוט לקחת את הגישה ההפוכה ולהזיז את העשרוני שמאלה על ידי מספר אפסים בכוח של עשר.
בואו נראה מה קורה כשאנחנו מחלקים את 1.9436 בכמה כוחות של 10.
\ [\ התחל {יישור}
1.9436\ div 10 & =0.19436\ n מספר בודד\\ 1.9436\ div 100 & =0.019436\ n מספר בודד\\
1.9436\ div 1000&=0.0019436\ n מספר אחרון\ סוף {יישור}\]
אם אין מספיק ספרות כדי להזיז את העשרוני, הוסף אפסים ליצירת מקומות.
סימון מדעי
סימון מדעי משמש לביטוי מספרים גדולים מאוד וקטנים מאוד כתוצר של שני מספרים. המספר הראשון של המוצר, המונח הספרה, הוא בדרך כלל מספר לא פחות מ 1 ולא יותר מ 10. המספר השני של המוצר, המונח האקספוננציאלי, כתוב כ- 10 עם אקספקטנט. כמה דוגמאות לסימון מדעי מובאות בטבלה\(\PageIndex{2}\).
| סימון רגיל | סימון מדעי |
|---|---|
| 1000 | 1 × 10 3 |
| 100 | 1 × 10 2 |
| 10 | 1 × 10 1 |
| 1 | 1 × 10 0 |
| 0.1 | 1 × 10 -1 |
| 0.01 | 1 × 10 -2 |
סימון מדעי הוא סימון שימושי במיוחד למספרים גדולים מאוד וקטנים מאוד, כגון 1,230,000,000 = 1.23 × 10 9, ו- 0.00000000036 = 3.6 × 10 −10.
הבעת מספרים בסימון מדעי
המרת כל מספר לסימון מדעי היא פשוטה. ספרו את מספר המקומות הדרושים להזזת העשרונית לצד הספרה השמאלית ביותר שאינה אפסית: כלומר, כדי להפוך את המספר בין 1 ל -10. ואז הכפל את המספר הזה ב -10 שהועלה למספר המקומות שהזזת את העשרוני. המעריך חיובי אם הזזת את העשרוני שמאלה ושלילית אם הזזת את העשרוני ימינה. אז
\[2386=2.386\times1000=2.386\times10^3\]
ו
\[0.123=1.23\times0.1=1.23\times10^{-1}\]
ההספק (אקספקטנט) של 10 שווה למספר המקומות שהעשרוני מוזז.
לוגריתמים
הלוגריתם הנפוץ (יומן) של מספר הוא הכוח אליו יש להעלות 10 כדי להיות שווה למספר זה. לדוגמה, הלוגריתם הנפוץ של 100 הוא 2, מכיוון שיש להעלות 10 לכוח השני כדי להיות שווה ל 100. דוגמאות נוספות נמצאות בטבלה\(\PageIndex{3}\).
| מספר | צורה מעריכית | לוגריתם נפוץ |
|---|---|---|
| 1000 | 10 3 | 3 |
| 10 | 10 1 | 1 |
| 1 | 10 0 | 0 |
| 0.1 | 10 -1 | -1 |
| 0.001 | 10 -3 | -3 |
כדי למצוא את הלוגריתם הנפוץ של רוב המספרים, יהיה עליך להשתמש בלחצן LOG במחשבון.
עיגול וספרות משמעותיות
בדיווח על נתונים מספריים המתקבלים באמצעות מדידות, אנו משתמשים רק בנתונים משמעותיים רבים ככל שדיוק המדידה מצדיק. לדוגמה, נניח שמיקרוביולוג המשתמש במונה תאים אוטומטי קובע שיש 525,341 תאים חיידקיים בדגימה של ליטר אחד של מי נהר. עם זאת, היא מתעדת את הריכוז כ -525,000 תאים לליטר ומשתמשת במספר מעוגל זה כדי להעריך את מספר התאים שכנראה יימצאו ב -10 ליטר מי נהר. במקרה זה, שלוש הספרות האחרונות של הכמות הנמדדת אינן נחשבות משמעותיות. הם מעוגלים כדי להסביר וריאציות במספר התאים שסביר להניח שיתרחשו אם נמדדו דגימות נוספות.
חשיבותם של נתונים משמעותיים טמונה ביישומם על חישוב יסודי. בנוסף וחיסור, הסכום או ההפרש צריכים להכיל כמה שיותר ספרות מימין לעשרוני כמו זה שבפחות בטוח (המצוין על ידי הדגשת הדוגמה הבאה) של המספרים המשמשים בחישוב.
נניח שמיקרוביולוג רוצה לחשב את המסה הכוללת של שתי דגימות אגר.
\ [\ התחל {array} {l}
4.38\ קו תחתון {3}\ טקסט {g}\\
\ קו תחתון {3.002\ קו תחתון {1}}\ טקסט {g}\
7.38\ קו תחתון {5}\ טקסט {g}\ סוף {מערך}\]
הפחות בטוח מבין שתי המסות כולל שלושה מקומות עשרוניים, כך שהסכום חייב להיות בעל שלוש נקודות עשרוניות.
בכפל ובחלוקה, המוצר או המנה צריכים להכיל לא יותר ספרות מאשר בגורם המכיל את המספר הנמוך ביותר של דמויות משמעותיות. נניח שהמיקרוביולוג ירצה לחשב כמה מגיב יהיה קיים ב-6.6 מ"ל אם הריכוז הוא 0.638 גרם/מ"ל.
\[\mathrm{0.63\underline{8}\:\dfrac{g}{mL}\times6.\underline{6}\:mL=4.1\:g}\]
שוב, לתשובה יש רק מקום עשרוני אחד מכיוון שזהו הדיוק של המספר הפחות מדויק בחישוב.
בעת עיגול מספרים, הגדל את הספרה השמורה ב -1 אם אחריה מספר גדול מ -5 ("עגול למעלה"). אל תשנה את הספרה השמורה אם הספרות הבאות הן פחות מ -5 ("סיבוב למטה"). אם אחרי הספרה השמורה אחריה 5, עיגול כלפי מעלה אם הספרה השמורה היא מוזרה, או עיגול כלפי מטה אם היא אחידה (לאחר העיגול, הספרה השמורה תמיד תהיה אחידה).
זמן דור
אפשר לכתוב משוואה לחישוב מספרי התאים בכל עת אם ידוע מספר תאי ההתחלה וזמן ההכפלה, כל עוד התאים מתחלקים בקצב קבוע. אנו מגדירים N 0 כמספר החיידקים ההתחלתי, המספר בזמן t = 0. N i הוא מספר החיידקים בזמן t = i, זמן שרירותי בעתיד. לבסוף נקבע j שווה למספר הדורות, או למספר הפעמים שאוכלוסיית התאים מכפילה במהלך מרווח הזמן. אז יש לנו,
\[N_i=N_0\times2^j\]
משוואה זו היא ביטוי לצמיחה על ידי ביקוע בינארי.
בדוגמה שלנו, N 0 = 4, מספר הדורות, j, שווה ל -3 אחרי 90 דקות מכיוון שזמן הייצור הוא 30 דקות. ניתן להעריך את מספר התאים מהמשוואה הבאה:
\ [\ להתחיל {ליישר}
N_I & =N_0\ פעמים2^j\ n מספר בודד\\ n
_ {90} &=4\ פעמים 2^3\ n\ n מספר בודד\\ n {90} &=4\ פעמים8=32\ n מספר יחיד\ סוף {יישור}\]
מספר התאים לאחר 90 דקות הוא 32.
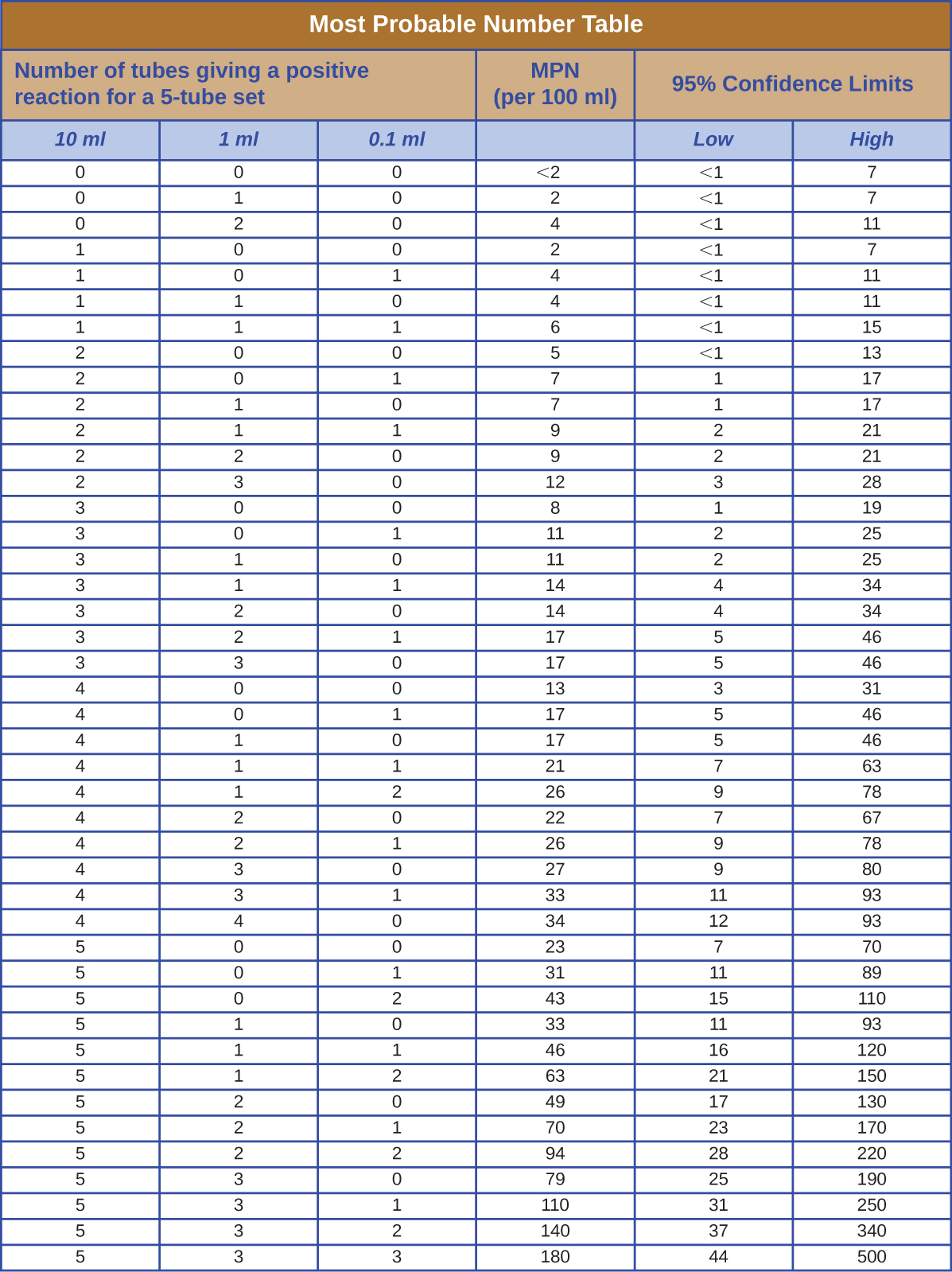
המספר הסביר ביותר
הטבלה באיור \(\PageIndex{1}\) מכילה ערכים המשמשים לחישוב דוגמת המספר הסבירה ביותר שניתנה ב- כיצד חיידקים גדלים.