7.4: מוצרים מיוחדים של פקטור
- Page ID
- 205463
בסוף פרק זה, תוכל:
- גורם טרינומי מרובע מושלם
- הבדלי גורמים של ריבועים
- סכומי פקטור והפרשי קוביות
- בחר שיטה לגורם פולינום לחלוטין
לפני שתתחיל, קח את חידון המוכנות הזה.
- פשט: \((12 x)^{2}\)
אם פספסת בעיה זו, עיין בתרגיל 6.2.22. - הכפל: \((m+4)^{2}\)
אם פספסת בעיה זו, עיין בתרגיל 6.4.1. - הכפל: \((p-9)^{2}\)
אם פספסת בעיה זו, עיין בתרגיל 6.4.4. - הכפל: \((k+3)(k-3)\)
אם פספסת בעיה זו, עיין בתרגיל 6.4.16.
האסטרטגיה לפקטורינג שפיתחנו בחלק האחרון תנחה אותך כשאתה מביא בחשבון את רוב הבינומים, הטרינומים והפולינומים עם יותר משלושה מונחים. ראינו שחלק מהבינומים והטרינומים נובעים ממוצרים מיוחדים - בינומים בריבוע ומכפילים מצמידים. אם אתה לומד לזהות סוגים אלה של פולינומים, אתה יכול להשתמש בדפוסי מוצרים מיוחדים כדי לחשב אותם הרבה יותר מהר.
טרינום מרובע מושלם של פקטור
חלק מהטרינומים הם ריבועים מושלמים. הם נובעים מכפלת פעמים בינומיות עצמה. ניתן לריבוע בינומי באמצעות FOIL, אך שימוש בתבנית הריבועים הבינומיים שראית בפרק הקודם חוסך לך שלב. בואו נסקור את תבנית הריבועים הבינומיים על ידי ריבוע בינומי באמצעות FOIL.
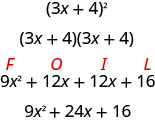
המונח הראשון הוא הריבוע של המונח הראשון של הבינום והמונח האחרון הוא הריבוע של האחרון. המונח האמצעי הוא כפול מהתוצר של שני המונחים של הבינום.
\[\begin{array}{c}{(3 x)^{2}+2(3 x \cdot 4)+4^{2}} \\ {9 x^{2}+24 x+16}\end{array}\]
הטרינום \(9 x^{2}+24+16\) נקרא טרינום מרובע מושלם. זהו הריבוע של הבינומי 3 x +4.
נחזור על תבנית הריבועים הבינומיים כאן כדי להשתמש בה כהפניה בפקטורינג.
אם a ו - b הם מספרים ממשיים,
\[(a+b)^{2}=a^{2}+2 a b+b^{2} \qquad(a-b)^{2}=a^{2}-2 a b+b^{2}\]
כאשר אתה מרובע בינומי, המוצר הוא טרינום מרובע מושלם. בפרק זה, אתם לומדים להביא בחשבון — כעת, תתחילו בטרינום מרובע מושלם ותכניסו אותו לגורמים העיקריים שלו.
אתה יכול לקחת בחשבון טרינום זה בשיטות המתוארות בסעיף האחרון, מכיוון שהוא מהצורה. \(ax^{2}+bx+c\) אבל אם תזהו שהמונחים הראשונים והאחרונים הם ריבועים והטרינום מתאים לדפוס הטרינומי המרובע המושלם, תחסוך לעצמך עבודה רבה.
הנה התבנית - ההפך של תבנית הריבועים הבינומיים.
אם a ו - b הם מספרים ממשיים,
\[a^{2}+2 a b+b^{2}=(a+b)^{2} \qquad a^{2}-2 a b+b^{2}=(a-b)^{2}\]
כדי להשתמש בדפוס זה, עליכם להכיר בכך שטרינום נתון מתאים לו. בדוק תחילה אם המקדם המוביל הוא ריבוע מושלם,\(a^2\). לאחר מכן בדוק שהמונח האחרון הוא ריבוע מושלם,\(b^2\). ואז בדוק את המונח האמצעי - האם זה כפול מהמוצר,? \(2ab\) אם הכל בודק, אתה יכול בקלות לכתוב את הגורמים.
גורם: \(9 x^{2}+12 x+4\)
- תשובה
-



גורם: \(4 x^{2}+12 x+9\)
- תשובה
-
\((2 x+3)^{2}\)
גורם: \(9 y^{2}+24 y+16\)
- תשובה
-
\((3 y+4)^{2}\)
הסימן של המונח האמצעי קובע באיזה דפוס נשתמש. כאשר המונח האמצעי הוא שלילי, אנו משתמשים בתבנית\(a^{2}-2 a b+b^{2}\), מה גורם ל\((a-b)^{2}\).
השלבים מסוכמים כאן.
\(\begin{array} {lcc} \textbf { Step 1} \text { . Does the trinomial fit the pattern? } & a^{2}+2 a b+b^{2} & a^{2}-2 a b+b^{2} \\ \qquad \bullet \text { Is the first term a perfect square? } & (a)^{2} & (a)^{2} \\ \qquad \quad\text { Write it as a square. } \\ \qquad \bullet \text { Is the last term a perfect square? } & (a)^{2} \qquad\quad (b)^{2} & (a)^{2} \qquad \quad(b)^{2} \\ \qquad \quad \text { Write it as a square. } \\ \qquad \bullet \text { Check the middle term. Is it } 2 a b ? & (a)^{2} \searrow_{2 \cdot a \cdot b }\swarrow(b)^{2} & (a)^{2} \searrow_{2 \cdot a \cdot b} \swarrow(b)^{2} \\ \textbf { Step 2} . \text { Write the square of the binomial. } & (a+b)^{2} & (a-b)^{2} \\ \textbf { Step 3} . \text { Check by multiplying. }\end{array}\)
נעבוד עכשיו אחד שבו טווח הביניים שלילי.
גורם: \(81 y^{2}-72 y+16\)
- תשובה
-
המונחים הראשונים והאחרונים הם ריבועים. בדוק אם המונח האמצעי מתאים לדפוס של טרינום מרובע מושלם. המונח האמצעי הוא שלילי, כך שהריבוע הבינומי יהיה. \((a-b)^{2}\)
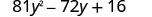
האם המונחים הראשונים והאחרונים הם ריבועים מושלמים? 
בדוק את טווח הביניים. 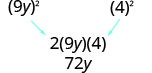
האם זה תואם\((a-b)^{2}\)? כן. 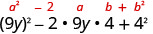
כתוב את הריבוע של בינומי. 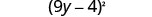
בדוק על ידי הכפלת. \((9 y-4)^{2}\) \((9 y)^{2}-2 \cdot 9 y \cdot 4+4^{2}\) \(81 y^{2}-72 y+16 \checkmark\)
גורם: \(64 y^{2}-80 y+25\)
- תשובה
-
\((8 y-5)^{2}\)
גורם: \(16 z^{2}-72 z+81\)
- תשובה
-
\((4 z-9)^{2}\)
הדוגמה הבאה תהיה טרינום מרובע מושלם עם שני משתנים.
גורם: \(36 x^{2}+84 x y+49 y^{2}\)
- תשובה
-
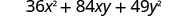
בדוק כל מונח כדי לאמת את התבנית. 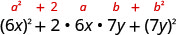
פקטור. 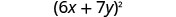
בדוק על ידי הכפלת. \((6 x+7 y)^{2}\) \((6 x)^{2}+2 \cdot 6 x \cdot 7 y+(7 y)^{2}\) \(36 x^{2}+84 x y+49 y^{2} \checkmark\)
גורם: \(49 x^{2}+84 x y+36 y^{2}\)
- תשובה
-
\((7 x+6 y)^{2}\)
גורם: \(64 m^{2}+112 m n+49 n^{2}\)
- תשובה
-
\((8 m+7 n)^{2}\)
גורם: \(9 x^{2}+50 x+25\)
- תשובה
-
\(\begin{array}{lc} & 9 x^{2}+50 x+25 \\ \text { Are the first and last terms perfect squares? } & (3 x)^{2} \qquad\quad (5)^2 \\ \text { Check the middle term-is it 2ab? } & (3 x)^{2} \searrow_{2(3 x)(5) }\swarrow (5)^{2}. \\ & \tiny{30x} \\ \text { No! } 30 x \neq 50 x & \text { This does not fit the pattern! } \\ \text { Factor using the "ac" method. } & 9 x^{2}+50 x+25 \\ \begin{array}{c}{\text { ac }} \\ {\text { Notice: } 9 \cdot 25 \text { and } 5 \cdot 45=225} \\ {225}\end{array} \\ {\text { Split the middle term. }} & \begin{array}{c}{9 x^{2}+5 x+45 x+25} \\ {x(9 x+5)+5(9 x+5)} \\ {(9 x+5)(x+5)}\end{array}\\ {\text { Factor by grouping. }} \\ \text { Check. } & \\ \begin{array}{l}{(9 x+5)(x+5)} \\ {9 x^{2}+45 x+5 x+25} \\ {9 x^{2}+50 x+25}\checkmark\end{array}\end{array}\)
גורם: \(16 r^{2}+30 r s+9 s^{2}\)
- תשובה
-
\((8 r+3 s)(2 r+3 s)\)
גורם: \(9 u^{2}+87 u+100\)
- תשובה
-
\((3 u+4)(3 u+25)\)
זוכר את הצעד הראשון באסטרטגיה שלנו לפקטורינג פולינומים? זה היה לשאול "האם יש גורם משותף גדול ביותר?" ואם היה, אתה מביא בחשבון את ה- GCF לפני שתמשיך הלאה. טרינומים מרובעים מושלמים עשויים להיות בעלי GCF בכל שלושת המונחים ויש לקחת זאת בחשבון תחילה. ולפעמים, ברגע ש- GCF נלקח בחשבון, תוכלו לזהות טרינום מרובע מושלם.
גורם: \(36 x^{2} y-48 x y+16 y\)
- תשובה
-
\(36 x^{2} y-48 x y+16 y\) האם יש GCF? כן, 4 שנים, אז קחו את זה בחשבון. 4 \(y\left(9 x^{2}-12 x+4\right)\) האם זה טרינום מרובע מושלם? אמת את התבנית. 
פקטור. 4 \(y(3 x-2)^{2}\) זכור: שמור את הגורם 4 y במוצר הסופי. בדוק. \(4y(3 x-2)^{2}\) \(4y[(3 x)^{2}-2 \cdot 3 x \cdot 2+2^{2}]\) \(4 y(9 x)^{2}-12 x+4\) \(36 x^{2} y-48 x y+16 y\checkmark\)
גורם: \(8 x^{2} y-24 x y+18 y\)
- תשובה
-
2 \(y(2 x-3)^{2}\)
גורם: \(27 p^{2} q+90 p q+75 q\)
- תשובה
-
3 \(q(3 p+5)^{2}\)
הבדלי גורמים בריבועים
המוצר המיוחד הנוסף שראית בקודם היה דפוס המוצר של מצמידים. השתמשת בזה כדי להכפיל שני בינומים שהיו מצומדים. הנה דוגמה:
\[\begin{array}{c}{(3 x-4)(3 x+4)} \\ {9 x^{2}-16}\end{array}\]
זכור, כאשר אתה מכפיל בינומים מצומדים, המונחים האמצעיים של המוצר מוסיפים ל-0. כל שנותר לך הוא בינומי, ההבדל בין ריבועים.
הכפלת מצומדים היא הדרך היחידה להשיג בינומיום מתוצר של שני בינומים.
אם a ו - b הם מספרים ממשיים
\[(a-b)(a+b)=a^{2}-b^{2}\]
המוצר נקרא הבדל של ריבועים.
כדי להביא בחשבון, נשתמש בתבנית המוצר "הפוך" כדי לחשב את ההבדל בריבועים. הבדל של ריבועים גורמים לתוצר של מצומדים.
אם a ו - b הם מספרים ממשיים,
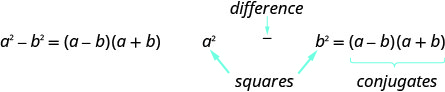
זכור, "הבדל" מתייחס לחיסור. לכן, כדי להשתמש בתבנית זו עליכם לוודא שיש לכם בינומיום בו מופחתים שני ריבועים.
גורם: \(x^{2}-4\)
- תשובה
-




גורם: \(h^{2}-81\)
- תשובה
-
\((h-9)(h+9)\)
גורם: \(k^{2}-121\)
- תשובה
-
\((k-11)(k+11)\)
\(\begin{array}{lc} \textbf { Step 1} . \text { Does the binomial fit the pattern? } & a^{2}-b^{2} \\ \qquad \bullet \text { Is this a difference? } & \underline{\quad} - \underline{\quad} \\ \qquad \bullet \text { Are the first and last terms perfect squares? } \\ \textbf { Step 2} . \text { Write them as squares. } & (a)^{2}-(b)^{2} \\ \textbf { Step 3.} \text{ Write the product of conjugates. } & (a-b)(a+b) \\ \textbf { Step 4.} \text{ Check by multiplying. } \end{array}\)
חשוב לזכור שסכומי ריבועים אינם גורמים לתוצר של בינומים. אין גורמים בינומיים שמתרבים יחד כדי לקבל סכום של ריבועים. לאחר הסרת כל GCF, הביטוי \(a^{2}+b^{2}\) הוא ראשוני!
אל תשכח ש -1 הוא ריבוע מושלם. נצטרך להשתמש בעובדה זו בדוגמה הבאה.
גורם: \(64 y^{2}-1\)
- תשובה
-
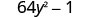
האם זה הבדל? כן. 
האם המונחים הראשונים והאחרונים הם ריבועים מושלמים? כן - כתוב אותם כריבועים. 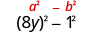
גורם כתוצר של מצמידים. 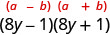
בדוק על ידי הכפלת. \((8 y-1)(8 y+1)\) \(64 y^{2}-1 \checkmark\)
גורם: \(m^{2}-1\)
- תשובה
-
\((m-1)(m+1)\)
גורם: \(81 y^{2}-1\)
- תשובה
-
\((9 y-1)(9 y+1)\)
גורם: \(121 x^{2}-49 y^{2}\)
- תשובה
-
\(\begin{array}{lc} & 121 x^{2}-49 y^{2} \\ \text { Is this a difference of squares? Yes. } & (11 x)^{2}-(7 y)^{2} \\ \text { Factor as the product of conjugates. } & (11 x-7 y)(11 x+7 y) \\ \text { Check by multiplying. } & \\ \begin{array}{l}{(11 x-7 y)(11 x+7 y)} \\ {121 x^{2}-49 y^{2}} \checkmark \end{array} \end{array}\)
גורם: \(196 m^{2}-25 n^{2}\)
- תשובה
-
\((16 m-5 n)(16 m+5 n)\)
גורם: \(144 p^{2}-9 q^{2}\)
- תשובה
-
\((12 p-3 q)(12 p+3 q)\)
הבינום בדוגמה הבאה עשוי להיראות "אחורה", אבל זה עדיין ההבדל בין הריבועים.
גורם: \(100-h^{2}\)
- תשובה
-
\(\begin{array}{lc} & 100-h^{2} \\ \text { Is this a difference of squares? Yes. } & (10)^{2}-(h)^{2}\\ \text { Factor as the product of conjugates. } & (10-h)(10+h)\\ \text { Check by multiplying. } & \\ \begin{array}{l}{(10-h)(10+h)} \\ {100-h^{2}} \checkmark \end{array} \end{array}\)
היזהר לא לשכתב את הביטוי המקורי כ\(h^{2}-100\).
פקטור \(h^{2}-100\) בעצמך ואז שים לב איך התוצאה שונה\((10-h)(10+h)\).
גורם: \(144-x^{2}\)
- תשובה
-
\((12-x)(12+x)\)
גורם: \(169-p^{2}\)
- תשובה
-
\((13-p)(13+p)\)
כדי לגבש לחלוטין את הבינום בדוגמה הבאה, נביא בחשבון הבדל של ריבועים פעמיים!
גורם: \(x^{4}-y^{4}\)
- תשובה
-
\(\begin{array}{lc}\text { Is this a difference of squares? Yes. } & {x^{4}-y^{4}} \\\text { Factor it as the product of conjugates. } & {\left(x^{2}\right)^{2}-\left(y^{2}\right)^{2}} \\ \text { Notice the first binomial is also a difference of squares! } & {\left(x^{2}-y^{2}\right)\left(x^{2}+y^{2}\right)} \\ \text { Factor it as the product of conjugates. The last }& {(x-y)(x+y)\left(x^{2}+y^{2}\right)} \\ \text { factor, the sum of squares, cannot be factored. } \\ \\ \text { Check by multiplying. } & \\\begin{array}{l}{(x-y)(x+y)\left(x^{2}+y^{2}\right)} \\ {[(x-y)(x+y)]\left(x^{2}+y^{2}\right)} \\ {\left(x^{2}-y^{2}\right)\left(x^{2}+y^{2}\right)} \\ {x^{4}-y^{4}} \checkmark \end{array} \end{array}\)
גורם: \(a^{4}-b^{4}\)
- תשובה
-
\(\left(a^{2}+b^{2}\right)(a+b)(a-b)\)
גורם: \(x^{4}-16\)
- תשובה
-
\(\left(x^{2}+4\right)(x+2)(x-2)\)
כמו תמיד, עליך לחפש גורם משותף תחילה בכל פעם שיש לך ביטוי לגורם. לפעמים גורם משותף עשוי "להסוות" את ההבדל בריבועים ולא תזהה את הריבועים המושלמים עד שתביא בחשבון את ה- GCF.
גורם: \(8 x^{2} y-98 y\)
- תשובה
-
\(\begin{array}{lc}& 8 x^{2} y-98 y \\ \text { Is there a GCF? Yes, } 2 y-\text { factor it out! } & 2 y\left(4 x^{2}-49\right) \\ \text { Is the binomial a difference of squares? Yes. } & 2 y\left((2 x)^{2}-(7)^{2}\right) \\ \text { Factor as a product of conjugates. } & 2 y(2 x-7)(2 x+7) \\ \text { Check by multiplying. } \\ \\ \begin{array}{l}{2 y(2 x-7)(2 x+7)} \\ {2 y[(2 x-7)(2 x+7)]} \\ {2 y\left(4 x^{2}-49\right)} \\ {8 x^{2} y-98 y} \checkmark \end{array} \end{array}\)
גורם: \(7 x y^{2}-175 x\)
- תשובה
-
7 \(x(y-5)(y+5)\)
גורם: \(45 a^{2} b-80 b\)
- תשובה
-
5 \(b(3 a-4)(3 a+4)\)
גורם: \(6 x^{2}+96\)
- תשובה
-
\(\begin{array}{lc}&6 x^{2}+96 \\ \text { Is there a GCF? Yes, } 6-\text { factor it out! } & 6\left(x^{2}+16\right) \\ \text { Is the binomial a difference of squares? No, it } & \\ \text { is a sum of squares. Sums of squares do not factor! } & \\ \text { Check by multiplying. } \\ \\ \begin{array}{l}{6\left(x^{2}+16\right)} \\ {6 x^{2}+96 }\checkmark \end{array} \end{array}\)
גורם: \(8 a^{2}+200\)
- תשובה
-
8 \(\left(a^{2}+25\right)\)
גורם: \(36 y^{2}+81\)
- תשובה
-
9 \(\left(4 y^{2}+9\right)\)
סכומי פקטור והבדלי קוביות
יש דפוס מיוחד נוסף לפקטורינג, כזה שלא השתמשנו בו כשהכפלנו פולינומים. זהו דפוס עבור סכום ההבדל של קוביות. נכתוב תחילה את הנוסחאות הללו ואז נבדוק אותן בכפל.
\[\begin{aligned} a^{3}+b^{3} &=(a+b)\left(a^{2}-a b+b^{2}\right) \\ a^{3}-b^{3} &=(a-b)\left(a^{2}+a b+b^{2}\right) \end{aligned}\]
אנו נבדוק את התבנית הראשונה ונשאיר לך את השנייה.
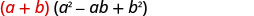 |
|
| להפיץ. |  |
| להכפיל. | \(a^{3}-a^{2} b+a b^{2}+a^{2} b-a b^{2}+b^{3}\) |
| לשלב מונחים כמו. | \(a^{3}+b^{3}\) |
\[\begin{array}{l}{a^{3}+b^{3}=(a+b)\left(a^{2}-a b+b^{2}\right)} \\ {a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)}\end{array}\]
שני הדפוסים נראים דומים מאוד, לא? אבל שימו לב לסימנים בגורמים. הסימן של הגורם הבינומי תואם את הסימן בבינומיום המקורי. והסימן של המונח האמצעי של הגורם הטרינומי הוא ההפך מהסימן בבינומיום המקורי. אם אתה מזהה את דפוס הסימנים, זה עשוי לעזור לך לשנן את הדפוסים.

לא ניתן לקחת בחשבון את הגורם הטרינומי בסכום ובהפרש של תבנית הקוביות.
זה יכול להועיל מאוד אם תלמד לזהות את קוביות המספרים השלמים מ -1 עד 10, ממש כמו שלמדת לזהות ריבועים. רשמנו את קוביות המספרים השלמים מ -1 עד 10 באיור\(\PageIndex{1}\).

גורם: \(x^{3}+64\)
- תשובה
-





גורם: \(x^{3}+27\)
- תשובה
-
\((x+3)\left(x^{2}-3 x+9\right)\)
גורם: \(y^{3}+8\)
- תשובה
-
\((y+2)\left(y^{2}-2 y+4\right)\)
כדי לחשב את הסכום או ההפרש של קוביות:
- האם הבינום מתאים לסכום או להפרש של תבנית הקוביות?
- האם זה סכום או הבדל?
- האם המונחים הראשונים והאחרונים הם קוביות מושלמות?
- כתוב אותם כקוביות.
- השתמש בסכום או בהפרש של תבנית קוביות.
- פשט בתוך הסוגריים
- בדוק על ידי הכפלת הגורמים.
גורם: \(: x^{3}-1000\)
- תשובה
-

הבינום הזה הוא הבדל. המונחים הראשונים והאחרונים הם קוביות מושלמות. כתוב את המונחים כקוביות. 
השתמש בהבדל של תבנית קוביות. 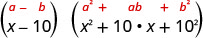
לפשט. 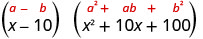
בדוק על ידי הכפלת. 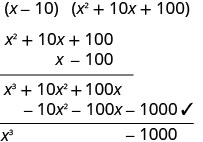
גורם: \(u^{3}-125\)
- תשובה
-
\((u-5)\left(u^{2}+5 u+25\right)\)
גורם: \(v^{3}-343\)
- תשובה
-
\((v-7)\left(v^{2}+7 v+49\right)\)
הקפד להשתמש בסימנים הנכונים בגורמי הסכום וההפרש של קוביות.
גורם: \(512-125 p^{3}\)
- תשובה
-

הבינום הזה הוא הבדל. המונחים הראשונים והאחרונים הם קוביות מושלמות. כתוב את המונחים כקוביות. 
השתמש בהבדל של תבנית קוביות. 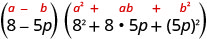
לפשט. 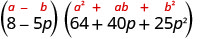
בדוק על ידי הכפלת. נשאיר לך את הצ'ק.
גורם: \(64-27 x^{3}\)
- תשובה
-
\((4-3 x)\left(16+12 x+9 x^{2}\right)\)
גורם: \(27-8 y^{3}\)
- תשובה
-
\((3-2 y)\left(9+6 y+4 y^{2}\right)\)
גורם: \(27 u^{3}-125 v^{3}\)
- תשובה
-

הבינום הזה הוא הבדל. המונחים הראשונים והאחרונים הם קוביות מושלמות. כתוב את המונחים כקוביות. 
השתמש בהבדל של תבנית קוביות. 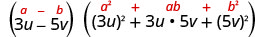
לפשט. 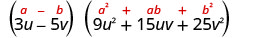
בדוק על ידי הכפלת. נשאיר לך את הצ'ק.
גורם: \(8 x^{3}-27 y^{3}\)
- תשובה
-
\((2 x-3 y)\left(4 x^{2}+6 x y+9 y^{2}\right)\)
גורם: \(1000 m^{3}-125 n^{3}\)
- תשובה
-
\((10 m-5 n)\left(100 m^{2}+50 m n+25 n^{2}\right)\)
בדוגמה הבאה, אנו מביאים בחשבון תחילה את ה- GCF. ואז נוכל לזהות את סכום הקוביות.
גורם: \(5 m^{3}+40 n^{3}\)
- תשובה
-
בדוק. כדי לבדוק, ייתכן שיהיה לך קל יותר להכפיל את סכום גורמי הקוביות תחילה, ואז להכפיל את המוצר ב -5. נשאיר לך את הכפל.
גורם הגורם המשותף. 
הבינום הזה הוא סכום. המונחים הראשונים והאחרונים הם קוביות מושלמות. כתוב את המונחים כקוביות. 
השתמש בסכום של תבנית קוביות. 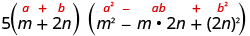
לפשט. 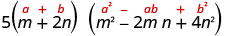
- 5 \((m+2 n)\left(m^{2}-2 m n+4 n^{2}\right)\)
גורם: \(500 p^{3}+4 q^{3}\)
- תשובה
-
4 \((5 p+q)\left(25 p^{2}-5 p q+q^{2}\right)\)
גורם: \(432 c^{3}+686 d^{3}\)
- תשובה
-
2 \((6 c+7 d)\left(36 c^{2}-42 c d+49 d^{2}\right)\)
גש למשאבים מקוונים אלה לקבלת הדרכה ותרגול נוספים עם פקטורינג מוצרים מיוחדים.
- סכום הפרש הקוביות
- ההבדל של קוביות פקטורינג
מושגי מפתח
- טרינומים מרובעים מושלמים של פקטור ראה דוגמה . \(\begin{array} {lcc} \textbf { Step 1} \text { . Does the trinomial fit the pattern? } & a^{2}+2 a b+b^{2} & a^{2}-2 a b+b^{2} \\ \qquad \bullet \text { Is the first term a perfect square? } & (a)^{2} & (a)^{2} \\ \qquad \quad\text { Write it as a square. } \\ \qquad \bullet \text { Is the last term a perfect square? } & (a)^{2} \qquad\quad (b)^{2} & (a)^{2} \qquad \quad(b)^{2} \\ \qquad \quad \text { Write it as a square. } \\ \qquad \bullet \text { Check the middle term. Is it } 2 a b ? & (a)^{2} \searrow_{2 \cdot a \cdot b }\swarrow(b)^{2} & (a)^{2} \searrow_{2 \cdot a \cdot b} \swarrow(b)^{2} \\ \textbf { Step 2} . \text { Write the square of the binomial. } & (a+b)^{2} & (a-b)^{2} \\ \textbf { Step 3} . \text { Check by multiplying. }\end{array}\)
- הבדלי גורמים של ריבועים ראה דוגמה. \(\begin{array}{lc} \textbf { Step 1} . \text { Does the binomial fit the pattern? } & a^{2}-b^{2} \\ \qquad \bullet \text { Is this a difference? } & \underline{\quad} - \underline{\quad} \\ \qquad \bullet \text { Are the first and last terms perfect squares? } \\ \textbf { Step 2} . \text { Write them as squares. } & (a)^{2}-(b)^{2} \\ \textbf { Step 3.} \text{ Write the product of conjugates. } & (a-b)(a+b) \\ \textbf { Step 4.} \text{ Check by multiplying. } \end{array}\)
- סכום גורם והפרש קוביות כדי לחשב את הסכום או ההפרש של הקוביות: ראה דוגמה.
- האם הבינום מתאים לסכום או להפרש של תבנית הקוביות? האם זה סכום או הבדל? האם המונחים הראשונים והאחרונים הם קוביות מושלמות?
- כתוב אותם כקוביות.
- השתמש בסכום או בהפרש של תבנית קוביות.
- פשט בתוך הסוגריים
- בדוק על ידי הכפלת הגורמים.
רשימת מילים
- דפוס טרינומי מרובע מושלם
- אם a ו - b הם מספרים ממשיים,
\[\begin{array}{cc} {a^2+2ab+b^2=(a+b)^2}&{a^2−2ab+b^2=(a−b)^2}\\ \nonumber \end{array}\]
- הבדל של דפוס ריבועים
- אם a ו - b הם מספרים ממשיים,

- סכום ההבדל של דפוס קוביות
-
\[\begin{array}{cc} {a^3+b^3=(a+b)(a^2−ab+b^2)}&{a^3−b^3=(a−b)(a^2+ab+b^2)}\\ \nonumber \end{array}\]


