3.5: לפתור יישומי תנועה אחידים
- Page ID
- 205465
בסוף פרק זה, תוכל:
- לפתור יישומי תנועה אחידים
לפני שתתחיל, קח את חידון המוכנות הזה.
- מצא את המרחק שעבר מכונית שעוברת 70 מייל לשעה למשך 3 שעות.
אם פספסת בעיה זו, עיין בתרגיל 2.6.1. - לפתור\(x+1.2(x−10)=98\).
אם פספסת בעיה זו, עיין בתרגיל 2.4.7. - המר 90 דקות לשעות.
אם פספסת בעיה זו, עיין בתרגיל 1.11.1.
לפתור יישומי תנועה אחידים
כאשר מתכננים טיול בכביש, זה עוזר לעתים קרובות לדעת כמה זמן ייקח להגיע ליעד או כמה רחוק לנסוע בכל יום. היינו משתמשים בנוסחת המרחק, הקצב והזמן, D = RT, שכבר ראינו.
בחלק זה נשתמש בנוסחה זו במצבים הדורשים מעט יותר אלגברה לפתרון מאלה שראינו קודם. באופן כללי, נבחן השוואה בין שני תרחישים, כמו שני רכבים הנוסעים בתעריפים שונים או בכיוונים מנוגדים. כאשר המהירות של כל רכב קבועה, אנו קוראים ליישומים כמו בעיות תנועה אחידות אלה.
אסטרטגיות פתרון הבעיות שלנו עדיין יחולו כאן, אך נוסיף לשלב הראשון. השלב הראשון יכלול ציור תרשים המציג את המתרחש בדוגמה. ציור התרשים עוזר לנו להבין מה קורה כדי שנכתוב משוואה מתאימה. לאחר מכן נכין טבלה לארגון המידע, כמו שעשינו עבור יישומי הכסף.
השלבים מפורטים כאן לעיון קל:
- קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.
- צייר תרשים כדי להמחיש מה זה קורה.
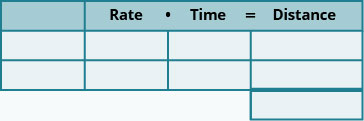
- צור טבלה לארגון המידע.
- תייג את קצב העמודות, הזמן, המרחק.
- רשום את שני התרחישים.
- כתוב במידע שאתה מכיר.
- זהה את מה שאנחנו מחפשים.
- תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.
- השלם את התרשים.
- השתמש בביטויים משתנים כדי לייצג את הכמות הזו בכל שורה.
- הכפל את הקצב כפול הזמן כדי לקבל את המרחק.
- תרגם למשוואה.
- שחזר את הבעיה במשפט אחד עם כל המידע החשוב.
- לאחר מכן, תרגם את המשפט למשוואה.
- לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
- בדוק את התשובה בבעיה וודא שהיא הגיונית.
- ענה על השאלה במשפט שלם.
רכבת אקספרס ורכבת מקומית יוצאים מפיטסבורג כדי לנסוע לוושינגטון הבירה הרכבת המהירה יכולה לבצע את הנסיעה תוך 4 שעות והרכבת המקומית אורכת 5 שעות לנסיעה. מהירות הרכבת המהירה היא 12 מייל לשעה מהר יותר ממהירות הרכבת המקומית. מצא את המהירות של שתי הרכבות.
- תשובה
-
שלב 1. קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.
צייר תרשים כדי להמחיש מה זה קורה. להלן סקיצה של מה שקורה בדוגמה.
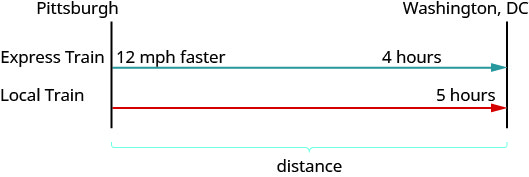
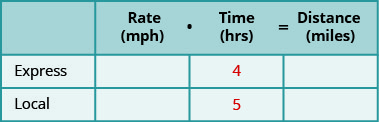
צור טבלה לארגון המידע. תייג את העמודות "דרג", "זמן" ו"מרחק". רשום את שני התרחישים. כתוב במידע שאתה מכיר.
שלב 2. זהה את מה שאנחנו מחפשים.
אנו מתבקשים למצוא את המהירות של שתי הרכבות. שימו לב שנוסחת המרחק משתמשת במילה "קצב", אך מקובל יותר להשתמש ב"מהירות "כשאנחנו מדברים על כלי רכב באנגלית יומיומית.
שלב 3. תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.
השלם את התרשים השתמש בביטויים משתנים כדי לייצג את הכמות בכל שורה. אנחנו מחפשים את המהירות של הרכבות. בואו בואו r לייצג את המהירות של הרכבת המקומית. מכיוון שמהירות הרכבת המהירה מהירה יותר ב -12 קמ"ש, אנו מייצגים את זה כ- r+12.
\[\begin{aligned} r &=\text { speed of the local train } \\ r+12 &=\text { speed of the express train } \end{aligned}\]
מלא את המהירויות בתרשים.
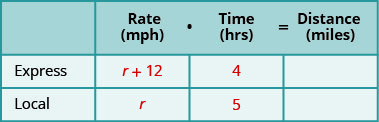
-
הכפל את הקצב כפול הזמן כדי לקבל את המרחק.
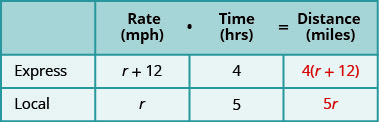
שלב 4. תרגם למשוואה.
שחזר את הבעיה במשפט אחד עם כל המידע החשוב. לאחר מכן, תרגם את המשפט למשוואה. 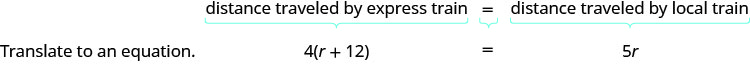
-
- המשוואה למודל מצב זה תגיע מהקשר בין המרחקים. תסתכל על התרשים שציירנו לעיל. כיצד המרחק שנסע ברכבת האקספרס קשור למרחק שנסעה ברכבת המקומית?
- מכיוון ששתי הרכבות עוזבות מפיטסבורג ונוסעות לוושינגטון הבירה הן נוסעות באותו מרחק. אז אנחנו כותבים:
שלב 5. לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
שלב 6. בדוק את התשובה בבעיה וודא שהיא הגיונית. \[\begin{array}{ll}{\text { express train }} & {60 \mathrm{mph}(4 \text { hours })=240 \mathrm{miles}} \\ {\text { local train }} & {48 \mathrm{mph}(5 \text { hours })=240 \mathrm{miles} \checkmark \end{array}\]עכשיו לפתור את המשוואה הזו. 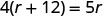
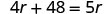
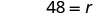
אז המהירות של הרכבת המקומית היא 48 קמ"ש.
מצא את המהירות של הרכבת המהירה. 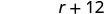


מהירות הרכבת המהירה היא 60 קמ"ש.
שלב 7. ענה על השאלה במשפט שלם.
מהירות הרכבת המקומית היא 48 קמ"ש ומהירות הרכבת המהירה היא 60 קמ"ש.
וויין ודניס אוהבים לרכוב על שביל האופניים מפארק ריברסייד לחוף הים. המהירות של דניס מהירה שבעה מיילים לשעה מהמהירות של וויין, כך שלוקח לוויין שעתיים לרכוב לחוף בזמן שלוקח לדניס 1.5 שעות לנסיעה. מצא את המהירות של שני האופנוענים.
- תשובה
-
וויין 21 קמ"ש, דניס 28 קמ"ש
ג'רומי יכול לנסוע מביתו בקליבלנד לקולג' שלו בשיקגו תוך 4.5 שעות. לוקח לאמא שלו 6 שעות לעשות את אותה נסיעה. ג'רומי נוהג 20 מייל לשעה מהר יותר מאמו. מצא את המהירות של ג'רומי ואת המהירות של אמו.
- תשובה
-
ג'רומי 80 קמ"ש, אמא 60 קמ"ש
בתרגיל\(\PageIndex{4}\), הדוגמה האחרונה, היו לנו שתי רכבות שנסעו באותו מרחק. התרשים והתרשים עזרו לנו לכתוב את המשוואה שפתרנו. בואו נראה איך זה עובד במקרה אחר.
כריסטופר והוריו גרים במרחק של 115 קילומטרים זה מזה. הם נפגשו במסעדה בין בתיהם כדי לחגוג את יום הולדתה של אמו. כריסטופר נסע 1.5 שעות בזמן שהוריו נסעו שעה אחת כדי להגיע למסעדה. המהירות הממוצעת של כריסטופר הייתה 10 מייל לשעה מהירה יותר מהמהירות הממוצעת של הוריו. מה היו המהירויות הממוצעות של כריסטופר ושל הוריו כשנסעו למסעדה?
- תשובה
-
שלב 1. קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.
צייר תרשים כדי להמחיש מה זה קורה. להלן מראה סקיצה של מה שקורה בדוגמה.
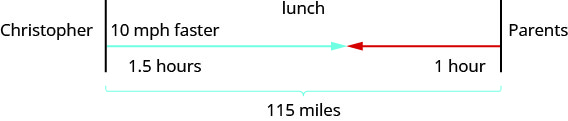
צור טבלה לארגון המידע.
תייג את קצב העמודות, הזמן, המרחק.
רשום את שני התרחישים.
כתוב במידע שאתה מכיר.
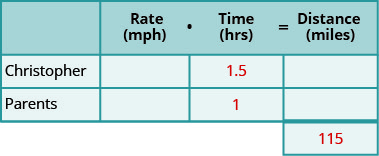
שלב 2. זהה את מה שאנחנו מחפשים.
אנו מתבקשים למצוא את המהירויות הממוצעות של כריסטופר והוריו.
שלב 3. תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.
השלם את התרשים. - השתמש בביטויים משתנים כדי לייצג את הכמות הזו בכל שורה.
- אנו מחפשים את המהירויות הממוצעות שלהם. בואו בואו r לייצג את המהירות הממוצעת של ההורים. מכיוון שמהירותו של כריסטופר מהירה יותר ב -10 קמ"ש, אנו מייצגים את זה כ- r+10.
-
מלא את המהירויות בתרשים.
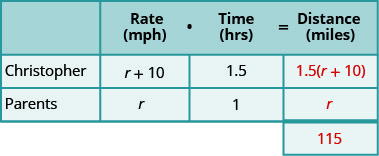
הכפל את הקצב כפול הזמן כדי לקבל את המרחק.
שלב 4. תרגם למשוואה.
שחזר את הבעיה במשפט אחד עם כל המידע החשוב. לאחר מכן, תרגם את המשפט למשוואה. שוב, עלינו לזהות קשר בין המרחקים על מנת לכתוב משוואה. התבונן בתרשים שיצרנו למעלה ושים לב לקשר בין המרחק שעבר כריסטופר למרחק שעברו הוריו.המרחק שכריסטופר נסע בתוספת המרחק שהוריו נוסעים חייב להסתכם ב -115 מיילים. אז אנחנו כותבים:

שלב 5. לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
\(\begin{array} {cc} {} &{1.5(r + 10) + r = 115} \\ {} &{1.5r + 15 + r = 115} \\ {\text{Now solve this equation.}} &{2.5r + 15 = 115} \\{} &{2.5r = 100} \\{} &{r = 40} \\ {} &{\text{so the parents' speed was 40 mph.}} \\ {} &{r + 10} \\ {\text{Christopher's speed is r + 10}} &{40 + 10} \\ {} &{50} \\ {} &{\text{Christopher's speed was 50 mph.}} \\ {} &{} \end{array}\)
שלב 6. בדוק את התשובה בבעיה וודא שהיא הגיונית.
\(\begin{array}{llll} {\text{Christopher drove}} &{50\text{ mph (1.5 hours)}} &{=} &{75\text{ miles}}\\ {\text{His parents drove}} &{40\text{ mph (1 hour)}} &{=} &{\underline{40 \text{ miles}}}\\ {} &{} &{} &{115\text{ miles}} \end{array}\)
\(\begin{array}{ll} {\textbf{Step 7. Answer}\text{ the question with a complete sentence.}} &{} \\{} &{\text{Christopher's speed was 50 mph.}}\\ {} &{\text{His parents' speed was 40 mph.}} \end{array}\)
קארינה נוסעת מביתה באנהיים לברקלי באותו יום שאחיה נוסע מברקלי לאנהיים, ולכן הם מחליטים להיפגש לארוחת צהריים בדרך בבאטונווילו. המרחק מאנהיים לברקלי הוא 410 מיילים. זה לוקח קארינה 3 שעות להגיע Buttonwillow, בעוד אחיה נוסע 4 שעות להגיע לשם. המהירות הממוצעת שאחיה של קרינה נסע הייתה מהירה ב -15 מייל לשעה מהמהירות הממוצעת של קרינה. מצא את המהירויות הממוצעות של קרינה ואחיה.
- תשובה
-
קארינה 50 קמ"ש, אח 65 קמ"ש
אשלי הולכת לקולג' במיניאפוליס, 234 קילומטרים מביתה בסיו פולס. היא רוצה שהוריה יביאו לה עוד בגדי חורף, ולכן הם מחליטים להיפגש במסעדה בכביש בין מיניאפוליס לסיו פולס. אשלי והוריה נסעו שעתיים למסעדה. המהירות הממוצעת של אשלי הייתה שבעה מיילים לשעה מהר יותר מהמהירות הממוצעת של הוריה. מצא את המהירות הממוצעת של אשלי ושל הוריה.
- תשובה
-
הורים 55 קמ"ש, אשלי 62 קמ"ש
כשאתה קורא את הדוגמה הבאה, חשוב על הקשר בין המרחקים שנסעו. איזו משתי הדוגמאות הקודמות דומה יותר למצב זה?
שני נהגי משאיות עוזבים אזור מנוחה בכביש המהיר בו זמנית. משאית אחת נוסעת מזרחה והשנייה נוסעת מערבה. המשאית הנוסעת מערבה נוסעת במהירות של 70 קמ"ש ולמשאית הנוסעת מזרחה מהירות ממוצעת של 60 קמ"ש. כמה זמן הם ייסעו לפני שהם יהיו במרחק של 325 קילומטרים זה מזה?
- תשובה
-
שלב 1. קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.
צייר תרשים כדי להמחיש מה זה קורה.
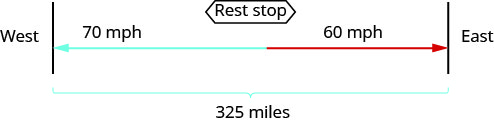
צור טבלה לארגון המידע.

שלב 2. זהה את מה שאנחנו מחפשים.
אנו מתבקשים למצוא את משך הזמן שהמשאיות ייסעו עד שהן יהיו במרחק של 325 קילומטרים זה מזה.
שלב 3. תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.
אנחנו מחפשים את הזמן שנסע. שתי המשאיות ייסעו באותה פרק זמן. בוא נקרא לזמן t. מכיוון שהמהירויות שלהם שונות, הם ייסעו מרחקים שונים. השלם את התרשים.
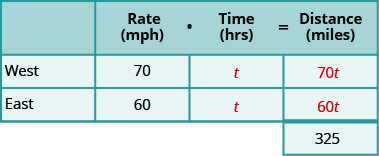
שלב 4. תרגם למשוואה.
עלינו למצוא קשר בין המרחקים כדי לכתוב משוואה. כשמסתכלים על התרשים, מה הקשר בין המרחק שכל אחת מהמשאיות תעבור? המרחק שעבר המשאית מערבה בתוספת המרחק שעברה המשאית מזרחה חייב להסתכם ב -325 מיילים. אז אנחנו כותבים:

שלב 5. לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
\[\begin{array} {lrll} {\text{Now solve this equation. }} & {70 t+60 t} &{=} &{325} \\ {} &{130 t} &{=} &{325} \\ {} &{t} &{=} &{2.5} \end{array}\]
שלב 6. בדוק את התשובה בבעיה וודא שהיא הגיונית.
\(\begin{array}{llll} {\text{Truck going West}} &{70\text{ mph (2.5 hours)}} &{=} &{175\text{ miles}}\\ {\text{Truck going East}} &{60\text{ mph (2.5 hour)}} &{=} &{\underline{150 \text{ miles}}}\\ {} &{} &{} &{325\text{ miles}} \end{array}\)
\(\begin{array}{ll} \\{\textbf{Step 7. Answer}\text{ the question with a complete sentence.}} &{\text{It will take the truck 2.5 hours to be 325 miles apart.}} \end{array}\)
פייר ומוניק עוזבים את ביתם בפורטלנד באותו זמן. פייר נוסע צפונה על הכביש המהיר במהירות של 75 מייל לשעה ואילו מוניק נוסעת דרומה במהירות של 68 מייל לשעה. כמה זמן ייקח להם להיות במרחק של 429 קילומטרים זה מזה?
- תשובה
-
3 שעות
תאן ונהאט עוזבים את משרדם בסקרמנטו במקביל. Thanh נוסע צפונה על I-5 במהירות של 72 מייל לשעה. נהאט נוסע דרומה על I-5 במהירות של 76 מייל לשעה. כמה זמן ייקח להם להיות במרחק של 330 קילומטרים זה מזה?
- תשובה
-
2.2 שעות
חשוב לוודא שהיחידות תואמות כאשר אנו משתמשים בקצב המרחק ובנוסחת הזמן. לדוגמה, אם התעריף הוא בקילומטרים לשעה, אז הזמן חייב להיות בשעות.
כשקייטי מיי הולכת לבית הספר, זה לוקח לה 30 דקות. אם היא רוכבת על האופניים שלה, זה לוקח לה 15 דקות. המהירות שלה מהירה יותר משלושה מיילים לשעה כשהיא רוכבת על אופניה מאשר כשהיא הולכת. מה מהירות ההליכה שלה והמהירות שלה רוכבת על האופניים שלה?
- תשובה
-
ראשית, אנו מציירים תרשים המייצג את המצב כדי לעזור לנו לראות מה קורה.
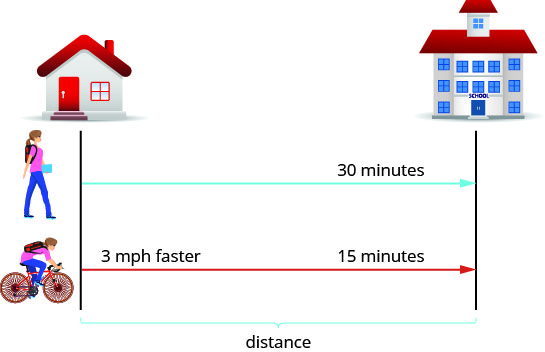
-
אנו מתבקשים למצוא את המהירות שלה בהליכה ורכיבה על אופניה. בוא נקרא לה מהירות הליכה r. מכיוון שמהירות האופניים שלה מהירה יותר משלושה מיילים לשעה, נקרא למהירות הזו r+3. אנו כותבים את המהירויות בתרשים.
המהירות היא בקילומטרים לשעה, ולכן עלינו לבטא גם את הזמנים בשעות, על מנת שהיחידות יהיו זהות. זכור, שעה אחת היא 60 דקות. אז:
\[\begin{array}{l}{30 \text { minutes is } \frac{30}{60} \text { or } \frac{1}{2} \text { hour }} \\ {15 \text { minutes is } \frac{15}{60} \text { or } \frac{1}{4} \text { hour }}\end{array}\]
לאחר מכן, אנו מכפילים קצב כפול זמן כדי למלא את עמודת המרחק.
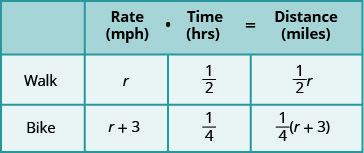
המשוואה תבוא מהעובדה שהמרחק מביתה של קייטי מיי לבית הספר שלה זהה בין אם היא הולכת או רוכבת על אופניה.
אז אנחנו אומרים:

תרגם למשוואה. 
לפתור את המשוואה הזו. 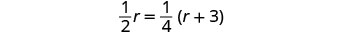
נקה את השברים על ידי הכפלת ה- LCD של כל השברים במשוואה. 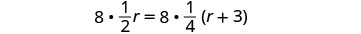
לפשט. 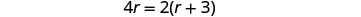
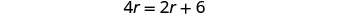


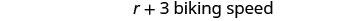

6 קמ"ש
(מהירות האופניים של קייטי מיי)בוא נבדוק אם זה עובד.
הליכה 3 קמ"ש (0.5 שעה) = 1.5 מייל
אופניים 6 קמ"ש (0.25 שעה) = 1.5 מיילכן, בכל מקרה קייטי מיי נוסעת 1.5 מייל לבית הספר. מהירות ההליכה של קייטי מיי היא 3 קמ"ש.
המהירות שלה לרכוב על האופניים שלה היא 6 קמ"ש.
לסוזי לוקח 50 דקות לטייל במעלה הגבעה מהחניון למגדל התצפית. לוקח לה 30 דקות לטייל בחזרה למגרש החניה. המהירות שלה בירידה מהירה ב -1.2 מייל לשעה מהמהירות שלה בעלייה. מצא את מהירות העלייה והירידה של סוזי.
- תשובה
-
בעלייה 1.8 קמ"ש, בירידה של שלושה קמ"ש
לואין לוקח 45 דקות להסיע את הסירה שלו במעלה הזרם מן המזח למקום הדיג האהוב עליו. לוקח לו 30 דקות להסיע את הסירה חזרה במורד הזרם לרציף. מהירות הסירה יורדת במורד הזרם היא 4 מייל לשעה מהירה יותר ממהירותה במעלה הזרם. מצא את המהירות במעלה ובמורד הזרם של הסירה.
- תשובה
-
במעלה הזרם 8 קמ"ש, במורד הזרם 12 קמ"ש
בנוסחת המרחק, הקצב והזמן, הזמן מייצג את משך הזמן שחלף בפועל (בשעות, דקות וכו '). אם בעיה נותנת לנו זמני התחלה וסיום כזמני שעון, עלינו למצוא את הזמן שחלף על מנת להשתמש בנוסחה.
המילטון אוהב לנסוע ללאס וגאס, 255 קילומטרים מביתו במחוז אורנג '. בנסיעתו האחרונה הוא עזב את ביתו בשעה 14:00. החלק הראשון של נסיעתו היה בכבישים מהירים בעיר. בשעה 16:00 התנועה התפנתה והוא הצליח לנסוע במדבר במהירות פי 1.75 מאשר כשנסע באזור הצפוף. הוא הגיע ללאס וגאס בשעה 18:30. כמה מהר הוא נהג בכל חלק מהטיול שלו?
- תשובה
-
תרשים יעזור לנו לדגמן את הטיול הזה.
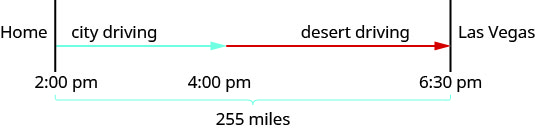
לאחר מכן, אנו יוצרים טבלה לארגון המידע.
אנו יודעים שהמרחק הכולל הוא 255 מיילים. אנו מחפשים את קצב המהירות לכל חלק בטיול. השיעור במדבר הוא פי 1.75 מהשיעור בעיר. אם נאפשר r = השיעור בעיר, אז השיעור במדבר הוא 1.75r.
הזמנים כאן ניתנים כזמני שעון. המילטון התחיל מהבית בשעה 14:00 ונכנס למדבר בשעה 16:30. אז הוא בילה שעתיים בנהיגה בכבישים המהירים הצפופים בעיר. ואז הוא נסע מהר יותר משעה 16:00 עד 18:30 במדבר. אז הוא נסע 2.5 שעות במדבר.
כעת, אנו מכפילים את התעריפים בזמנים.
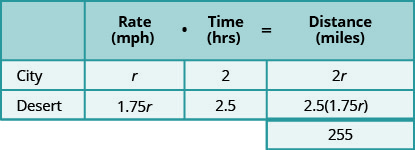
על ידי התבוננות בתרשים שלהלן, אנו יכולים לראות כי סכום המרחק שנסע בעיר והמרחק שנסע במדבר הוא 255 מיילים.
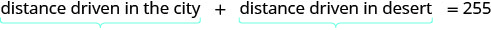
תרגם למשוואה. 
לפתור את המשוואה הזו. 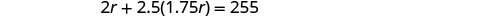
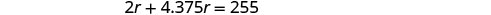
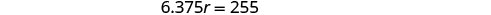
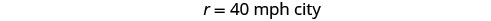
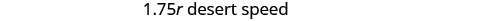
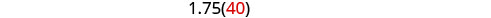
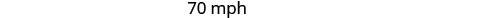
בדוק.

המילטון נסע 40 קמ"ש בעיר ו -70 קמ"ש במדבר.
קרוז מתאמן להתחרות בטריאתלון. הוא עזב את ביתו בשעה 6:00 ורץ עד השעה 7:30. ואז הוא רכב על אופניו עד 9:45. הוא כיסה מרחק כולל של 51 קילומטרים. המהירות שלו ברכיבה על אופניים הייתה פי 1.6 ממהירותו בזמן הריצה. מצא את מהירויות האופניים והריצה של קרוז.
- תשובה
-
רכיבה על אופניים 16 קמ"ש, ריצה 10 קמ"ש
פונג עזב את הבית על אופניו בשעה 10:00. הוא רכב ברחוב השטוח עד 11:15, ואז רכב במעלה הגבעה עד 11:45. הוא רכב בסך הכל 31 קילומטרים. הרכיבה המהירה שלו במעלה הגבעה הייתה פי 0.6 ממהירותו ברחוב השטוח. מצא את אופני המהירות שלו במעלה הגבעה וברחוב השטוח.
- תשובה
-
במעלה הגבעה 12 קמ"ש, רחוב שטוח 20 קמ"ש
מושגי מפתח
- מרחק, קצב וזמן
- D = rt כאשר D = מרחק, r = קצב, t = זמן
- אסטרטגיה לפתרון בעיות - יישומי מרחק, קצב וזמן
- קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.
צייר תרשים כדי להמחיש מה זה קורה.
צור טבלה לארגון המידע: תייג את העמודות קצב, זמן, מרחק. רשום את שני התרחישים. כתוב במידע שאתה מכיר. - זהה את מה שאנחנו מחפשים.
- תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.
השלם את התרשים.
השתמש בביטויים משתנים כדי לייצג את הכמות הזו בכל שורה.
הכפל את הקצב כפול הזמן כדי לקבל את המרחק. - תרגם למשוואה.
שחזר את הבעיה במשפט אחד עם כל המידע החשוב.
לאחר מכן, תרגם את המשפט למשוואה. - לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
- בדוק את התשובה בבעיה וודא שהיא הגיונית.
- ענה על השאלה במשפט שלם.
- קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.


