3.1: השתמש באסטרטגיה לפתרון בעיות

מטרות למידה

בסוף פרק זה תוכל:

• גש לבעיות מילים בגישה חיובית
• השתמש באסטרטגיה לפתרון בעיות לבעיות מילים
• לפתור בעיות מספרים

הערה

לפני שתתחיל, קח את חידון המוכנות הזה.

1. תרגם את "6 פחות מפעמיים x" לביטוי אלגברי.
   אם פספסת בעיה זו, סקור את תרגיל 1.3.43.
2. לפתור:$\frac{2}{3}x=24$.
   אם פספסת בעיה זו, עיין בתרגיל 2.2.10.
3. לפתור:$3x+8=14$.
   אם פספסת בעיה זו, עיין בתרגיל 2.3.1.

גישה לבעיות מילים בגישה חיובית

"אם אתה חושב שאתה יכול... או חושב שאתה לא יכול... אתה צודק." הנרי פורד

העולם מלא בבעיות מילים! האם ההכנסה שלי תאפשר לי לשכור את הדירה הזו? כמה אגרוף אני צריך להכין למסיבה? איזה גודל יהלום אני יכול להרשות לעצמי לקנות את החברה שלי? האם עלי לטוס או לנסוע למפגש המשפחתי שלי? כמה כסף אני צריך כדי למלא את המכונית עם דלק? כמה טיפ כדאי להשאיר במסעדה? כמה גרביים אני צריך לארוז לחופשה? איזה גודל הודו אני צריך לקנות לארוחת חג ההודיה, ואז באיזו שעה אני צריך להכניס אותו לתנור? אם אחותי ואני נקנה לאמא שלנו מתנה, כמה כל אחד מאיתנו משלם?

כעת, כשאנחנו יכולים לפתור משוואות, אנו מוכנים ליישם את הכישורים החדשים שלנו לבעיות מילים. האם אתה מכיר מישהו שעבר חוויות שליליות בעבר עם בעיות מילים? האם אי פעם היו לך מחשבות כמו התלמיד למטה (איור$\PageIndex{1}$)?

איור$\PageIndex{1}$: מחשבות שליליות יכולות להוות חסמים להצלחה.

כאשר אנו מרגישים שאין לנו שליטה, וממשיכים לחזור על מחשבות שליליות, אנו מציבים חסמים להצלחה. אנחנו צריכים להרגיע את הפחדים שלנו ולשנות את הרגשות השליליים שלנו.

התחל עם צפחה חדשה והתחל לחשוב מחשבות חיוביות. אם ניקח שליטה ונאמין שנוכל להצליח, נוכל לשלוט בבעיות מילים! קרא את המחשבות החיוביות באיור $\PageIndex{2}$ ואמר אותן בקול רם.

איור$\PageIndex{2}$: חשיבה של מחשבות חיוביות היא צעד ראשון לקראת הצלחה.

תחשוב על משהו, מחוץ לבית הספר, שאתה יכול לעשות עכשיו אבל לא יכולת לעשות לפני 3 שנים. האם הוא נוהג במכונית? סנובורד? מבשלים ארוחת גורמה? מדברים בשפה חדשה? חוויות העבר שלך עם בעיות מילים התרחשו כשהיית צעיר יותר - עכשיו אתה מבוגר ומוכן להצליח!

השתמש באסטרטגיה לפתרון בעיות לבעיות Word

סקרנו תרגום ביטויים באנגלית לביטויים אלגבריים, תוך שימוש באוצר מילים וסמלים מתמטיים בסיסיים. תרגמנו גם משפטים באנגלית למשוואות אלגבריות ופתרנו כמה בעיות מילים. המילה בעיות יישמה מתמטיקה על מצבים יומיומיים. הצבנו מחדש את המצב במשפט אחד, הקצנו משתנה ואז כתבנו משוואה לפתרון הבעיה. שיטה זו עובדת כל עוד המצב מוכר והמתמטיקה אינה מסובכת מדי.

כעת, נרחיב את האסטרטגיה שלנו כדי שנוכל להשתמש בה כדי לפתור בהצלחה כל בעיית מילים. נפרט את האסטרטגיה כאן, ואז נשתמש בה כדי לפתור כמה בעיות. אנו מסכמים להלן אסטרטגיה יעילה לפתרון בעיות.

השתמש באסטרטגיה לפתרון בעיות כדי לפתור בעיות WORD.

1. קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.
2. זהה את מה שאנחנו מחפשים.
3. תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.
4. תרגם למשוואה. זה עשוי להיות מועיל לשחזר את הבעיה במשפט אחד עם כל המידע החשוב. לאחר מכן, תרגם את המשפט האנגלי למשוואה אלגברית.
5. לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
6. בדוק את התשובה בבעיה וודא שהיא הגיונית.
7. ענה על השאלה במשפט שלם.

תרגיל $\PageIndex{1}$

פילאר קנה ארנק למכירה עבור$$18$, המהווה מחצית מהמחיר המקורי. מה היה המחיר המקורי של הארנק?

תשובה

שלב 1. קרא את הבעיה. קרא את הבעיה פעמיים או יותר במידת הצורך. חפש מילים לא מוכרות במילון או באינטרנט.

בבעיה זו, האם ברור על מה נדון? האם כל מילה מוכרת?

תן p = המחיר המקורי של הארנק.

שלב 2. זהה את מה שאתה מחפש. האם אי פעם נכנסת לחדר השינה שלך לקנות משהו ואז שכחת מה חיפשת? קשה למצוא משהו אם אתה לא בטוח מה זה! קרא שוב את הבעיה וחפש מילים שיגידו לך מה אתה מחפש!

בבעיה זו, המילים "מה היה המחיר המקורי של הארנק" לספר לנו מה אנחנו צריכים למצוא.

שלב 3. תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו. אנו יכולים להשתמש בכל אות עבור המשתנה, אך לבחור אחת שמקלה על זכירת מה היא מייצגת.

שלב 4. תרגם למשוואה. זה עשוי להיות מועיל לשחזר את הבעיה במשפט אחד עם כל המידע החשוב. תרגם את המשפט האנגלי למשוואה אלגברית.

קרא שוב את הבעיה בזהירות כדי לראות כיצד המידע הנתון קשור. לעתים קרובות, יש משפט אחד שנותן מידע זה, או שהוא עשוי לעזור לכתוב משפט אחד עם כל המידע החשוב. חפש מילות רמז שיעזרו לתרגם את המשפט לאלגברה. תרגם את המשפט למשוואה.

שחזר את הבעיה במשפט אחד עם כל המידע החשוב.	$\color{cyan} \underbrace{\strut \color{black}\mathbf{18}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\color{black}\textbf{one-half the original price.}}$
תרגם למשוואה.	$18 \qquad = \qquad \qquad \qquad \frac{1}{2}\cdot p$

שלב 5. לפתור את המשוואה באמצעות טכניקות אלגבריות טובות. גם אם אתה יודע את הפיתרון מייד, שימוש בטכניקות אלגבריות טובות כאן יכין אותך טוב יותר לפתור בעיות שאין להן תשובות ברורות.

לפתור את המשוואה.	$18 = \frac{1}{2}p$
הכפל את שני הצדדים ב -2.	${\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p$
לפשט.	$36 = p$

שלב 6. בדוק את התשובה בבעיה כדי לוודא שהיא הגיונית. פתרנו את המשוואה ומצאנו את זה$p=36$, שפירושו "המחיר המקורי" היה$$36$.

האם 36 דולר הגיוניים בבעיה? כן, כי 18 הוא חצי של 36, ואת הארנק היה על מכירה במחצית המחיר המקורי.

אם זה היה תרגיל שיעורי בית, העבודה שלנו עשויה להיראות כך:

פילאר קנתה ארנק למכירה עבור$$18$, שהוא חצי מהמחיר המקורי. מה היה המחיר המקורי של הארנק?

שלב 7. ענה על השאלה במשפט שלם. הבעיה שאלה "מה היה המחיר המקורי של הארנק?"

התשובה לשאלה היא: "המחיר המקורי של הארנק היה 36$."

	תן $p =$ את המחיר המקורי.
	$18$הוא חצי מהמחיר המקורי.
	$18 = \frac{1}{2}p$
הכפל את שני הצדדים על ידי$2$.	${\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p$
לפשט.	$36 = p$
בדוק. האם $$36$ מחיר סביר עבור ארנק?
כן.
האם חצי $18$ אחד של$36$?
$18 \stackrel{?}{=} \frac{1}{2}\cdot 36$
$18 = 18\checkmark$
	המחיר המקורי של הארנק היה$$36$.

תרגיל $\PageIndex{2}$

חואקין קנה כוננית למכירה$$120$, שהייתה שני שלישים מהמחיר המקורי. מה היה המחיר המקורי של ארון הספרים?

תשובה

$$180$

תרגיל $\PageIndex{3}$

שתי חמישיות מהשירים בפלייליסט של מריאל הם קאנטרי. אם יש שירי $16$ קאנטרי, מה המספר הכולל של השירים ברשימת ההשמעה?

תשובה

$40$

בואו ננסה גישה זו עם דוגמה נוספת.

תרגיל $\PageIndex{4}$

ג'יני וחבריה לכיתה הקימו קבוצת לימוד. מספר הבנות בקבוצת המחקר היה שלוש יותר מפי שניים ממספר הבנים. היו $11$ בנות בקבוצת המחקר. כמה בנים היו בקבוצת המחקר?

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.	כמה בנים היו בקבוצת המחקר?
שלב 3. שם. בחר משתנה שייצג את מספר הבנים.	תן $n=$ את מספר הבנים.
שלב 4. תרגם. שחזר את הבעיה במשפט אחד עם כל המידע החשוב.	$\color{cyan} \underbrace{\color{black}\textbf{The number}\\ \color{black}\textbf{of girls}(11)} \quad \underbrace{\strut \text{ } \\ \color{black}\textbf{was}} \quad \underbrace{\color{black}\textbf{three more than}\\ \color{black}\textbf{twice the number of boys}}$
תרגם למשוואה.	$\qquad 11 \qquad \quad = \qquad \qquad \quad 2b + 3$
שלב 5. לפתור את המשוואה.	$\quad 11 = 2b + 3$
הפחת 3 מכל צד.	$\quad 11 \,{\color{red}{- \,3}} = 2b + 3 \,{\color{red}{- \,3}}$
לפשט.	$\quad 8 = 2b$
מחלקים כל צד ב -2.	$\quad \dfrac{8}{\color{red}{2}}=\dfrac{2b}{\color{red}{2}}$
לפשט.	$\quad 4 = b$
שלב 6. בדוק. ראשית, האם התשובה שלנו סבירה? כן, יש $4$ בנים בקבוצת לימוד נראה בסדר. הבעיה אומרת שמספר הבנות היה $3$ יותר מפי שניים ממספר הבנים. אם יש ארבעה בנים, האם זה הופך לאחת עשרה בנות? פעמיים $4$ בנים זה$8$. שלושה יותר ממה $8$ שהוא$11$.
שלב 7. תענה על השאלה.	היו $4$ נערים בקבוצת המחקר.

תרגיל $\PageIndex{5}$

גילרמו קנה ספרי לימוד ומחברות בחנות הספרים. מספר ספרי הלימוד היה $3$ יותר מפי שניים ממספר המחברות. הוא קנה $7$ ספרי לימוד. כמה מחברות הוא קנה?

תשובה

$2$

תרגיל $\PageIndex{6}$

גרי עבד השבוע על חידות סודוקו ותשבצים. מספר חידות הסודוקו שהשלים הוא שמונה יותר מפי שניים ממספר התשבצים. הוא השלים חידות $22$ סודוקו. כמה תשבצים הוא עשה?

תשובה

$7$

לפתור בעיות מספרים

כעת, כשיש לנו אסטרטגיה לפתרון בעיות, נשתמש בה בכמה סוגים שונים של בעיות מילים. הסוג הראשון עליו נעבוד הוא "בעיות מספרים". בעיות מספרים נותנות כמה רמזים לגבי מספר אחד או יותר. אנו משתמשים ברמזים אלה כדי לכתוב משוואה. בעיות מספרים בדרך כלל אינן מתעוררות על בסיס יומיומי, אך הן מספקות מבוא טוב לתרגול האסטרטגיה לפתרון בעיות שתוארה לעיל.

תרגיל $\PageIndex{7}$

ההבדל בין מספר לשש הוא$13$. מצא את המספר.

תשובה

שלב 1. קרא את הבעיה. האם כל המילים מוכרות?
שלב 2. זהה את מה שאנחנו מחפשים.	המספר
שלב 3. שם. בחר משתנה שייצג את המספר.	תן $n=$ את המספר.
שלב 4. תרגם. זכור לחפש מילות רמז כמו "הבדל... של... ו..."
להחזיר את הבעיה כמשפט אחד.	$\color{cyan} \underbrace{\color{black}\textbf{The difference of the number and }\mathbf{6}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\strut \color{black}\mathbf{13}}$
תרגם למשוואה.	$\qquad \qquad \qquad n-6 \qquad \qquad \qquad \quad = \quad 13$
שלב 5. לפתור את המשוואה.	$\quad n - 6 = 13$
לפשט.	$\quad n =19$
שלב 6. בדוק.
ההבדל של $19$ ו $6$ הוא$13$. זה בודק!
שלב 7. תענה על השאלה.	המספר הוא$19$.

תרגיל $\PageIndex{8}$

ההבדל בין מספר לשמונה הוא$17$. מצא את המספר.

תשובה

$25$

תרגיל $\PageIndex{9}$

ההבדל בין מספר לאחת עשרה הוא$−7$. מצא את המספר.

תשובה

$4$

תרגיל $\PageIndex{10}$

סכום כפול מספר ושבע הוא$15$. מצא את המספר.

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.	המספר
שלב 3. שם. בחר משתנה שייצג את המספר.	תן $n =$ את המספר.
שלב 4. תרגם.
להחזיר את הבעיה כמשפט אחד.
תרגם למשוואה.
שלב 5. לפתור את המשוואה.
הפחת 7 מכל צד ופשט.
מחלקים כל צד ב -2 ופשטו.
שלב 6. בדוק.
האם הסכום של פעמיים 4 ו -7 שווה ל -15?
$\begin{array} {rrl} {2\cdot 4 + 7} &{\stackrel{?}{=}}& {15} \\ {15} &{=} &{15\checkmark} \end{array}$
שלב 7. תענה על השאלה.	המספר הוא$4$.

שמתם לב שהשמטנו חלק מהצעדים כשפתרנו את המשוואה הזו? אם אתה עדיין לא מוכן לעזוב את השלבים האלה, רשום כמה שאתה צריך.

תרגיל $\PageIndex{11}$

הסכום של ארבע פעמים מספר ושניים הוא$14$. מצא את המספר.

תשובה

$3$

תרגיל $\PageIndex{12}$

הסכום של שלוש פעמים מספר ושבע הוא$25$. מצא את המספר.

תשובה

$6$

כמה בעיות במילות מספרים מבקשות מאיתנו למצוא שני מספרים או יותר. זה אולי מפתה לקרוא לכולם עם משתנים שונים, אך עד כה פתרנו רק משוואות עם משתנה אחד. על מנת להימנע משימוש ביותר ממשתנה אחד, נגדיר את המספרים במונחים של אותו משתנה. הקפד לקרוא את הבעיה בעיון כדי לגלות כיצד כל המספרים קשורים זה לזה.

תרגיל $\PageIndex{13}$

מספר אחד הוא חמישה יותר ממספר אחר. סכום המספרים הוא 21. מצא את המספרים.

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.		אנחנו מחפשים שני מספרים.
שלב 3. שם. יש לנו שני מספרים לתת שם וצריכים שם לכל אחד.
בחר משתנה שייצג את המספר הראשון.		תן $n=1^{st}$ מספר.
מה אנחנו יודעים על המספר השני?		מספר אחד הוא חמישה יותר ממספר אחר.
		$n+5=2^{nd}$מספר
שלב 4. תרגם. שחזר את הבעיה כמשפט אחד עם כל המידע החשוב.		סכום המספר ^הראשון והמספר ^השני הוא 21.
תרגם למשוואה.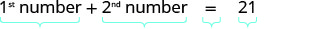
החלף את הביטויים המשתנים.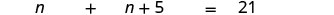
שלב 5. לפתור את המשוואה.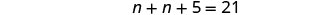
לשלב מונחים כמו.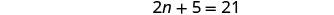
הפחת 5 משני הצדדים ופשט.
מחלקים ב -2 ופשטו.
מצא גם את המספר השני.
שלב 6. בדוק.
האם המספרים האלה בודקים את הבעיה?
האם מספר אחד $5$ יותר מהשני?	$13\stackrel{?}{=} 8 + 5$
שלוש עשרה זה $5$ יותר$8$? כן.	$13 = 13\checkmark$
האם הסכום של שני המספרים$21$?	$8 + 13 \stackrel{?}{=} 21$
	$21 = 21\checkmark$
שלב 7. תענה על השאלה.		המספרים הם $8$ ו$13$.

תרגיל $\PageIndex{14}$

מספר אחד הוא שישה יותר ממספר אחר. סכום המספרים הוא עשרים וארבע. מצא את המספרים.

תשובה

9, 15

תרגיל $\PageIndex{15}$

הסכום של שני מספרים הוא חמישים ושמונה. מספר אחד הוא ארבעה יותר מהשני. מצא את המספרים.

תשובה

27, 31

תרגיל $\PageIndex{16}$

הסכום של שני מספרים הוא שלילי 14. מספר אחד הוא ארבעה פחות מהשני. מצא את המספרים.

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.		אנחנו מחפשים שני מספרים.
שלב 3. שם.
בחר משתנה.		תן $n=1^{st}$ מספר.
מספר אחד הוא 4 פחות מהשני.		$n−4=2^{nd}$מספר
שלב 4. תרגם.
כתוב כמשפט אחד.		הסכום של שני המספרים הוא שלילי 14.
תרגם למשוואה.
שלב 5. לפתור את המשוואה.
לשלב מונחים כמו.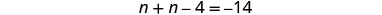
הוסף 4 לכל צד ופשט.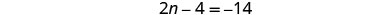
לפשט.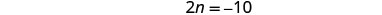
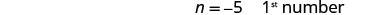
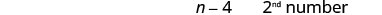
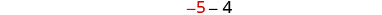
שלב 6. בדוק.
האם −9 ארבעה פחות מ -5?	$-5-4\stackrel{?}{=}-9$
	$-9 = -9 \checkmark$
האם הסכום הוא 14?	$-5+ (-9)\stackrel{?}{=}-14$
	$-14 = -14 \checkmark$
שלב 7. תענה על השאלה.		המספרים הם -5 ו -9.

תרגיל $\PageIndex{17}$

הסכום של שני מספרים הוא שלילי עשרים ושלוש. מספר אחד הוא שבעה פחות מהשני. מצא את המספרים.

תשובה

-15, -8

תרגיל $\PageIndex{18}$

סכום של שני מספרים הוא$−18$. מספר אחד הוא $40$ יותר מהשני. מצא את המספרים.

תשובה

-29, 11

תרגיל $\PageIndex{19}$

מספר אחד הוא עשרה יותר מפעמיים. הסכום שלהם הוא אחד. מצא את המספרים.

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאתה מחפש.		אנחנו מחפשים שני מספרים.
שלב 3. שם.
בחר משתנה.		תן $x=1^{st}$ מספר.
מספר אחד הוא 10 יותר מפעמיים.		$2x+10=2^{nd}$מספר
שלב 4. תרגם.
לחזור כמשפט אחד.		הסכום שלהם הוא אחד.
		סכום שני המספרים הוא 1.
תרגם למשוואה.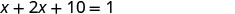
שלב 5. לפתור את המשוואה.
לשלב מונחים כמו.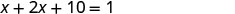
הפחת 10 מכל צד.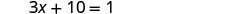
מחלקים כל צד ב -3.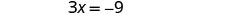
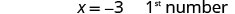
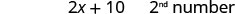
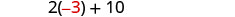
שלב 6. בדוק.
האם עשר יותר מפעמיים -3 שווה ל -4?	$2(-3) + 10 \stackrel{?}{=} 4$
	$-6 + 10 \stacktel{?}{=} 4$
	$4 = 4\checkmark$
האם הסכום שלהם הוא 1?	$-3 + 4 \stackrel{?}{=} 1$
	$1 = 1\checkmark$
שלב 7. תענה על השאלה.		המספרים הם -3 ו -4.

תרגיל $\PageIndex{20}$

מספר אחד הוא שמונה יותר מפעמיים. הסכום שלהם הוא שלילי ארבעה. מצא את המספרים.

תשובה

$-4,\; 0$

תרגיל $\PageIndex{21}$

מספר אחד הוא שלוש יותר משלוש פעמים אחר. הסכום שלהם הוא$−5$. מצא את המספרים.

תשובה

$-3,\; -2$

כמה בעיות במספר כוללות מספרים שלמים רצופים. מספרים שלמים רצופים הם מספרים שלמים העוקבים זה אחר זה מייד. דוגמאות למספרים שלמים רצופים הם:

$$\begin{array}{l}{1,2,3,4} \\ {-10,-9,-8,-7} \\ {150,151,152,153}\end{array}$$

שימו לב שכל מספר הוא אחד יותר מהמספר שקדם לו. אז אם נגדיר את המספר השלם הראשון כ$n$, המספר השלם הבא ברציפות הוא. $n+1$ זה שאחרי זה הוא אחד יותר מ$n+1$, כך הוא$n+1+1$, שהוא$n+2$.
$$\begin{array}{ll}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text { consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}$$

תרגיל $\PageIndex{22}$

הסכום של שני מספרים שלמים רצופים הוא$47$. מצא את המספרים.

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאתה מחפש.	שני מספרים שלמים רצופים
שלב 3. תן שם לכל מספר.	תן $n=1^{st}$ מספר שלם.
	$n+1=$המספר השלם הבא ברציפות
שלב 4. תרגם.
לחזור כמשפט אחד.	סכום המספרים השלמים הוא$47$.
תרגם למשוואה.
שלב 5. לפתור את המשוואה.
לשלב מונחים כמו.
הפחת 1 מכל צד.
מחלקים כל צד ב -2.
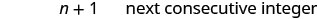
שלב 6. בדוק.
$\begin{array} {lll} {23 + 24} &{\stackrel{?}{=}} &{47} \\ {47} &{=} &{47\checkmark} \end{array}$
שלב 7. תענה על השאלה.	שני המספרים השלמים ברציפות הם 23 ו -24.

תרגיל $\PageIndex{23}$

הסכום של שני מספרים שלמים רצופים הוא 95. מצא את המספרים.

תשובה

47, 48

תרגיל $\PageIndex{24}$

הסכום של שני מספרים שלמים רצופים הוא -31. מצא את המספרים.

תשובה

-16, -15

תרגיל $\PageIndex{25}$

מצא שלושה מספרים שלמים רצופים שסכומם הוא -42.

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.	שלושה מספרים שלמים רצופים
שלב 3. תן שם לכל אחד משלושת המספרים.	תן $n=1^{st}$ מספר שלם.
	$n+1= 2^{nd}$מספר שלם רצוף
	$n+2= 3^{rd}$מספר שלם רצוף
שלב 4. תרגם.
לחזור כמשפט אחד.	הסכום של שלושת המספרים השלמים הוא$−42$.
תרגם למשוואה.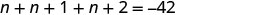
שלב 5. לפתור את המשוואה.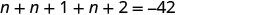
לשלב מונחים כמו.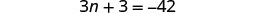
הפחת 3 מכל צד.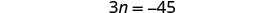
מחלקים כל צד ב -3.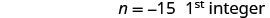
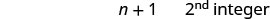
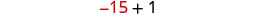
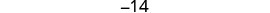
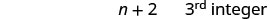
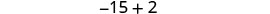
שלב 6. בדוק.
$\begin{array}{lll} {-13 + (-14) + (-15)} &{\stackrel{?}{=}} &{-42} \\ {-42} &{=} &{-42\checkmark} \end{array}$
שלב 7. תענה על השאלה.	שלושת המספרים השלמים ברציפות הם -13, -14 ו- -15.

תרגיל $\PageIndex{26}$

מצא שלושה מספרים שלמים רצופים שסכומם הוא -96.

תשובה

-33, -32, -31

תרגיל $\PageIndex{27}$

מצא שלושה מספרים שלמים רצופים שסכומם הוא -36.

תשובה

-13, -12, -11

כעת, לאחר שעבדנו עם מספרים שלמים רצופים, נרחיב את עבודתנו כך שתכלול מספרים שלמים רצופים ומספרים שלמים מוזרים רצופים. מספרים שלמים אפילו רצופים הם אפילו מספרים שלמים שמיד עוקבים זה אחר זה. דוגמאות למספרים שלמים רצופים הם:

$$\begin{array}{l}{18,20,22} \\ {64,66,68} \\ {-12,-10,-8}\end{array}$$

שימו לב שכל מספר שלם הוא $2$ יותר מהמספר שקדם לו. אם אנחנו קוראים את הראשון$n$, אז הבא הוא$n+2$. הבא יהיה $n+2+2$ או$n+4$.
$$\begin{array}{cll}{n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}$$

מספרים שלמים מוזרים רצופים הם מספרים שלמים מוזרים שמיד עוקבים זה אחר זה. קחו למשל את המספרים השלמים המוזרים ברציפות$77$,$79$, ו$81$.

$$\begin{array}{l}{77,79,81} \\ {n, n+2, n+4}\end{array}$$

$$\begin{array}{cll}{n} & {1^{\text { st }} \text {odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}$$

האם זה נראה מוזר להוסיף 2 (מספר זוגי) כדי להגיע ממספר שלם מוזר אחד למשנהו? האם אתה מקבל מספר אי זוגי או מספר זוגי כשאנחנו מוסיפים 2 ל -3? עד 11? עד 47?

בין אם הבעיה מבקשת מספרים זוגיים רצופים או מספרים אי-זוגיים, אינך צריך לעשות דבר שונה. התבנית עדיין זהה - כדי להגיע ממספר אחד מוזר או מספר שלם אחד למשנהו, הוסף 2.

תרגיל $\PageIndex{28}$

מצא שלושה מספרים שלמים רצופים שסכומם 84.

תשובה

$$\begin{array}{ll} {\textbf{Step 1. Read} \text{ the problem.}} & {} \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} & {\text{three consecutive even integers}} \\ {\textbf{Step 3. Name} \text{ the integers.}} & {\text{Let } n = 1^{st} \text{ even integers.}} \\ {} &{n + 2 = 2^{nd} \text{ consecutive even integer}} \\ {} &{n + 4 = 3^{rd} \text{ consecutive even integer}} \\ {\textbf{Step 4. Translate.}} &{} \\ {\text{ Restate as one sentence. }} &{\text{The sum of the three even integers is 84.}} \\ {\text{Translate into an equation.}} &{n + n + 2 + n + 4 = 84} \\ {\textbf{Step 5. Solve} \text{ the equation. }} &{} \\ {\text{Combine like terms.}} &{n + n + 2 + n + 4 = 84} \\ {\text{Subtract 6 from each side.}} &{3n + 6 = 84} \\ {\text{Divide each side by 3.}} &{3n = 78} \\ {} &{n = 26 \space 1^{st} \text{ integer}} \\\\ {} &{n + 2\space 2^{nd} \text{ integer}} \\ {} &{26 + 2} \\ {} &{28} \\\\ {} &{n + 4\space 3^{rd} \text{ integer}} \\ {} &{26 + 4} \\ {} &{30} \\ {\textbf{Step 6. Check.}} &{} \\\\ {26 + 28 + 30 \stackrel{?}{=} 84} &{} \\ {84 = 84 \checkmark} & {} \\ {\textbf{Step 7. Answer} \text{ the question.}} &{\text{The three consecutive integers are 26, 28, and 30.}} \end{array}$$

תרגיל $\PageIndex{29}$

מצא שלושה מספרים שלמים רצופים שסכומם 102.

תשובה

32, 34, 36

תרגיל $\PageIndex{30}$

מצא שלושה מספרים שלמים רצופים שסכומם הוא -24.

תשובה

−10, −8, −6

תרגיל $\PageIndex{31}$

זוג נשוי מרוויח יחד 110 אלף דולר בשנה. האישה מרוויחה 16,000 דולר פחות מכפליים ממה שבעלה מרוויח. מה הבעל מרוויח?

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.	כמה מרוויח הבעל?
שלב 3. שם.
בחר משתנה שייצג את הסכום שהבעל מרוויח.	תן $h=$ את הסכום שהבעל מרוויח.
האישה מרוויחה $$16,000$ פחות מפי שניים מזה.	$2h−16,000$הסכום שהאישה מרוויחה.
שלב 4. תרגם.	יחד הבעל והאישה מרוויחים$$110,000$.
שחזר את הבעיה במשפט אחד עם כל המידע החשוב.
תרגם למשוואה.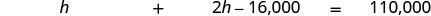
שלב 5. לפתור את המשוואה.	$h + 2h − 16,000 = 110,000$
לשלב מונחים כמו.	$3h − 16,000 = 110,000$
הוסף $16,000$ לשני הצדדים ופשט.	$3h = 126,000$
מחלקים כל צד על ידי$3$.	$h = 42,000$
	$$42,000$סכום שהבעל מרוויח
	$2h − 16,000$סכום האישה מרוויחה
	$2(42,000) − 16,000$
	$84,000 − 16,000$
	$68,000$
שלב 6. בדוק.
אם האישה מרוויחה $$68,000$ והבעל מרוויח $$42,000$ הוא סך הכל $$110,000$ (? כן!
שלב 7. תענה על השאלה.	הבעל מרוויח $$42,000$ שנה.

תרגיל $\PageIndex{32}$

על פי איגוד סוחרי הרכב הלאומי, העלות הממוצעת של מכונית בשנת 2014 הייתה 28,500 דולר. זה היה 1,500 דולר פחות מפי 6 מהעלות בשנת 1975. מה הייתה העלות הממוצעת של מכונית בשנת 1975?

תשובה

5000 דולר

תרגיל $\PageIndex{33}$

מנתוני מפקד האוכלוסין האמריקאי עולה כי המחיר החציוני של בית חדש בארצות הברית בנובמבר 2014 היה 280,900 דולר. זה היה 10,700 דולר יותר מפי 14 מהמחיר בנובמבר 1964. מה היה המחיר החציוני של בית חדש בנובמבר 1964?

תשובה

19300 דולר

מושגי מפתח

• אסטרטגיה לפתרון בעיות
  1. קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.
  2. זהה את מה שאנחנו מחפשים.
  3. תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.
  4. תרגם למשוואה. זה עשוי להיות מועיל לשחזר את הבעיה במשפט אחד עם כל המידע החשוב. לאחר מכן, תרגם את המשפט האנגלי למשוואת אלגברה.
  5. לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
  6. בדוק את התשובה בבעיה וודא שהיא הגיונית.
  7. ענה על השאלה במשפט שלם.
• מספרים שלמים רצופים מספרים שלמים
  רצופים הם מספרים שלמים העוקבים זה אחר זה מיד.

  $$\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text {consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}$$

  
  מספרים שלמים אפילו רצופים הם אפילו מספרים שלמים שמיד עוקבים זה אחר זה.

  $$\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}$$

  
  מספרים שלמים מוזרים רצופים הם מספרים שלמים מוזרים שמיד עוקבים זה אחר זה.

  $$\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}$$