פרק 1 תרגילי סקירה
- Page ID
- 205648
תרגילי סקירת פרקים
מבוא למספרים שלמים
השתמש בערך מקום עם מספר שלם
בתרגילים הבאים למצוא את ערך המקום של כל ספרה.
26,915
- 1
- 2
- 9
- 5
- 6
- תשובה
-
- עשרות
- עשרת אלפים
- מאות
- אלה
- אלפים
359,417
- 9
- 3
- 4
- 7
- 1
58,129,304
- 5
- 0
- 1
- 8
- 2
- תשובה
-
- עשרה מיליון
- עשרות
- מאות אלפים
- מיליונים
- עשרת אלפים
9,430,286,157
- 6
- 4
- 9
- 0
- 5
בתרגילים הבאים, שם כל מספר.
6,104
- תשובה
-
ששת אלפים, מאה וארבעה
493,068
3,975,284
- תשובה
-
שלושה מיליון, תשע מאות שבעים וחמישה אלף, מאתיים שמונים וארבעה
85,620,435
בתרגילים הבאים, כתוב כל מספר כמספר שלם באמצעות ספרות.
שלוש-מאות חמישה-עשר
- תשובה
-
315
שישים וחמישה אלף, תשע מאות שנים-עשר
תשעים מיליון, ארבע מאות עשרים וחמישה אלף, שש עשרה
- תשובה
-
90,425,016
מיליארד, ארבעים ושלושה מיליון, תשע מאות עשרים ושניים אלף, שלוש מאות אחד-עשר
בתרגילים הבאים, עגול לערך המקום המצוין.
סיבוב לעשירייה הקרובה ביותר.
- 407
- 8,564
- תשובה
-
- 410
- 8,560
סיבוב למאה הקרובה ביותר.
- 25,846
- 25,864
בתרגילים הבאים, עגול כל מספר ל -1. מאה 2. אלף 3. עשרת אלפים.
864,951
- תשובה
-
- 865,000865,000
- 865,000865,000
- 860,000
3,972,849
זיהוי מכפילים וגורמים
בתרגילים הבאים, השתמש במבחני החלוקה כדי לקבוע אם כל מספר מתחלק ב -2, ב -3, ב -5, ב -6 וב -10.
168
- תשובה
-
על ידי 2,3,6
264
375
- תשובה
-
על ידי 3,5
750
1430
- תשובה
-
על ידי 2,5,10
1080
מצא פקטוריזציות ראשוניות ומכפילים פחות נפוצים
בתרגילים הבאים, מצא את הפקטוריזציה העיקרית.
420
- תשובה
-
2 \(\cdot 2 \cdot 3 \cdot 5 \cdot 7\)
115
225
- תשובה
-
3 \(\cdot 3 \cdot 5 \cdot 5\)
2475
1560
- תשובה
-
\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 5 \cdot 13\)
56
72
- תשובה
-
\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 3\)
168
252
- תשובה
-
\(2 \cdot 2 \cdot 3 \cdot 3 \cdot 7\)
391
בתרגילים הבאים, מצא את הכפולה הפחות נפוצה של המספרים הבאים בשיטת הכפולות.
6,15
- תשובה
-
30
60, 75
בתרגילים הבאים, מצא את הכפולה הפחות נפוצה של המספרים הבאים בשיטת הגורמים הראשוניים.
24, 30
- תשובה
-
120
70, 84
השתמש בשפת האלגברה
השתמש במשתנים ובסמלים אלגבריים
בתרגילים הבאים, תרגם את הדברים הבאים מאלגברה לאנגלית.
25—7
- תשובה
-
25 מינוס 7, ההבדל של עשרים וחמש ושבע
5 \(\cdot 6\)
\(45 \div 5\)
- תשובה
-
45 מחולק על ידי 5, המנה של ארבעים וחמש וחמש
x+8
\(42 \geq 27\)
- תשובה
-
ארבעים ושתיים גדול או שווה לעשרים ושבע
3n=24
\(3 \leq 20 \div 4\)
- תשובה
-
3 הוא פחות או שווה ל 20 חלקי 4, שלוש פחות או שווה למנה של עשרים וארבע
\(a \neq 7 \cdot 4\)
בתרגילים הבאים, קבע אם כל אחד מהם הוא ביטוי או משוואה.
\(6 \cdot 3+5\)
- תשובה
-
ביטוי
י−8=32
פשט ביטויים באמצעות סדר הפעולות
בתרגילים הבאים, לפשט כל ביטוי.
\(3^{5}\)
- תשובה
-
243
\(10^{8}\)
בתרגילים הבאים, לפשט
6+10/2+2
- תשובה
-
13
9+12/3+4
\(20 \div(4+6) \cdot 5\)
- תשובה
-
10
\(33 \div(3+8) \cdot 2\)
\(4^{2}+5^{2}\)
- תשובה
-
41
\((4+5)^{2}\)
הערך ביטוי
בתרגילים הבאים, הערך את הביטויים הבאים.
9x+7 כאשר x = 3
- תשובה
-
34
5 איקס−4 כאשר x = 6
\(x^{4}\)מתי \(x=3\)
- תשובה
-
81
\(3^{x}\)מתי \(x=3\)
\(x^{2}+5 x-8\)מתי \(x=6\)
- תשובה
-
58
\(2 x+4 y-5\)מתי
\(x=7, y=8\)
פשט ביטויים על ידי שילוב מונחים דומים
בתרגילים הבאים, זהה את המקדם של כל מונח.
12n
- תשובה
-
12
9 \(x^{2}\)
בתרגילים הבאים, זהה את המונחים הדומים.
\(3 n, n^{2}, 12,12 p^{2}, 3,3 n^{2}\)
- תשובה
-
12 \(3, n^{2}\) ו- 3 \(n^{2}\)
\(5,18 r^{2}, 9 s, 9 r, 5 r^{2}, 5 s\)
בתרגילים הבאים, זהה את המונחים בכל ביטוי.
\(11 x^{2}+3 x+6\)
- תשובה
-
\(11 x^{2}, 3 x, 6\)
\(22 y^{3}+y+15\)
בתרגילים הבאים, פשט את הביטויים הבאים על ידי שילוב מונחים דומים.
17a+9 א
- תשובה
-
26 א
18 ז+9z
9x+3x+8
- תשובה
-
12x+8
8a+5a+9
7 עמ+6+5p−4
- תשובה
-
12p+2
8 איקס+7+4איקס−5
תרגם ביטוי באנגלית לביטוי אלגברי
בתרגילים הבאים, תרגם את הביטויים הבאים לביטויים אלגבריים.
סכום של 8 ו -12
- תשובה
-
8+12
הסכום של 9 ו -1
ההבדל בין x ו- 4
- תשובה
-
איקס-4
ההבדל בין x ו- 3
המוצר של 6 ו- y
- תשובה
-
6 שנים
המוצר של 9 ו- y
אדל קנתה חצאית וחולצה. החצאית עלתה 15 דולר יותר מהחולצה. תן bb לייצג את העלות של החולצה. כתוב ביטוי לעלות החצאית.
- תשובה
-
ב+15
למרסלה יש 6 פחות בני דודים מבני דודים מאשר בנות דודות. תן ל- g לייצג את מספר בנות הדודות. כתוב ביטוי למספר בני הדודים.
הוספה וחיסור של מספרים שלמים
השתמש בתשלילים וניגודים של מספרים שלמים
בתרגילים הבאים, סדר כל אחד מזוגות המספרים הבאים, באמצעות < or >.
- 6___2
- −7___4
- −9___−1
- 9___−3
- תשובה
-
- >
- <
- <
- >
- -5___1
- -4___−9
- 6___10
- 3___−8
בתרגילים הבאים,, מצא את ההפך מכל מספר.
- −8
- 1
- תשובה
-
- 8
- -1
- -2
- 6
בתרגילים הבאים, לפשט.
− (-19)
- תשובה
-
19
− (-53)
בתרגילים הבאים, לפשט.
−m כאשר
- מ = 3
- m=−3
- תשובה
-
- -3
- 3
−p כאשר
- p=6
- p=−6
פשט ביטויים עם ערך מוחלט
בתרגילים הבאים,, לפשט.
- |7|
- |−25|
- |0|
- תשובה
-
- 7
- 25
- 0
- |5|
- |0|
- |−19|
בתרגילים הבאים, מלא <, >, או = עבור כל אחד מזוגות המספרים הבאים.
- −8___|−8|
- −|−2|___−2
- תשובה
-
- <
- =
- |−3|___−|−3|
- 4___−|-4|
בתרגילים הבאים, לפשט.
|8-4|
- תשובה
-
4
|9—6|
8 (14-2 | −2|)
- תשובה
-
80
6 (13-4 | −2|)
בתרגילים הבאים, להעריך.
1. איקס| מתי איקס=−28
- תשובה
-
- 28
- 15
- yכאשר y = −37
- |−z | מתי ז = −24
הוסף מספרים שלמים
בתרגילים הבאים, לפשט כל ביטוי.
-200+65
- תשובה
-
-135
-150+45
2+ (-8) +6
- תשובה
-
0
4+ (-9) +7
140+ (-75) +67
- תשובה
-
132
-32+24+ (-6) +10
הפחת מספרים שלמים
בתרגילים הבאים, לפשט.
9—3
- תשובה
-
6
−5− (-1)
- 15—6
- 15+ (-6)
- תשובה
-
- 9
- 9
- 12—9
- 12+ (-9)
- 8− (-9)
- 8+9
- תשובה
-
- 17
- 17
- 4− (-4)
- 4+4
בתרגילים הבאים, לפשט כל ביטוי.
10− (-19)
- תשובה
-
29
11− (-18)
31—79
- תשובה
-
-48
39—81
−31—11
- תשובה
-
-42
-32—18
−15− (-28) +5
- תשובה
-
18
71+ (-10) -8
−16− (-4+1) −7
- תשובה
-
-20
−15− (-6+4) -3
הכפל מספרים שלמים
בתרגילים הבאים, הכפל.
-5 (7)
- תשובה
-
-35
-8 (6)
-18 (-2)
- תשובה
-
36
−10 (−6)
מחלקים מספרים שלמים
בתרגילים הבאים, לחלק.
\(-28 \div 7\)
- תשובה
-
-4
\(56 \div(-7)\)
\(-120 \div(-20)\)
- תשובה
-
6
\(-200 \div 25\)
פשט ביטויים עם מספרים שלמים
בתרגילים הבאים, לפשט כל ביטוי.
-8 (-2) -3 (-9)
- תשובה
-
43
−7 (-4) -5 (-3)
\((-5)^{3}\)
- תשובה
-
-125
\((-4)^{3}\)
\(-4 \cdot 2 \cdot 11\)
- תשובה
-
-88
\(-5 \cdot 3 \cdot 10\)
\(-10(-4) \div(-8)\)
- תשובה
-
-5
\(-8(-6) \div(-4)\)
31—4 (3—9)
- תשובה
-
55
24—3 (2—10)
הערכת ביטויים משתנים עם מספרים שלמים
בתרגילים הבאים, הערך כל ביטוי.
x+8 מתי
- איקס=−26
- איקס=−95
- תשובה
-
- -18
- -87
y+9 מתי
- y=−29
- y=−84
מתי b = −11, הערך:
- b+6
- −ב+6
- תשובה
-
- -5
- 17
מתי c = −9, הערך:
- ג+ (-4) ג+ (-4)
- −ג+ (-4)
\(p^{2}-5 p+2\)מתי
\(p=-1\)
- תשובה
-
8
\(q^{2}-2 q+9\)מתי \(q=-2\)
\(6 x-5 y+15\)מתי \(x=3\) ו \(y=-1\)
- תשובה
-
38
\(3 p-2 q+9\)מתי \(p=8\) ו \(q=-2\)
תרגם ביטויים באנגלית לביטויים אלגבריים
בתרגילים הבאים, תרגם לביטוי אלגברי ופשט במידת האפשר.
הסכום של -4 ו -17, גדל ב -32
- תשובה
-
(-4+ (-17)) +32; 11
- ההבדל של 15 ו -7
- לחסר 15 מ -7
המנה של -45 ו -9
- תשובה
-
\(\frac{-45}{-9} ; 5\)
התוצר של -12 וההבדל של c ו- d
השתמש במספרים שלמים ביישומים
בתרגילים הבאים, לפתור.
טמפרטורה הטמפרטורה הגבוהה יום אחד במיאמי ביץ ', פלורידה, הייתה 76°. באותו יום הטמפרטורה הגבוהה בבאפלו, ניו יורק הייתה -8°. מה ההבדל בין הטמפרטורה במיאמי ביץ 'לטמפרטורה בבאפלו?
- תשובה
-
84 מעלות
חשבון עובר ושב לאדריאן יש יתרה של -22 דולר בחשבון העובר ושב שלה. היא מפקידה 301 דולר לחשבון. מהו האיזון החדש?
דמיינו שברים
מצא שברים שווים
בתרגילים הבאים, מצא שלושה שברים המקבילים לשבר הנתון. הצג את העבודה שלך, באמצעות דמויות או אלגברה.
\(\frac{1}{4}\)
- תשובה
-
\(\frac{2}{8}, \frac{3}{12}, \frac{4}{16}\)התשובות עשויות להשתנות
\(\frac{1}{3}\)
\(\frac{5}{6}\)
- תשובה
-
\(\frac{10}{12}, \frac{15}{18}, \frac{20}{24}\)התשובות עשויות להשתנות
\(\frac{2}{7}\)
פשט שברים
בתרגילים הבאים, לפשט.
\(\frac{7}{21}\)
- תשובה
-
\(\frac{1}{3}\)
\(\frac{8}{24}\)
\(\frac{15}{20}\)
- תשובה
-
\(\frac{3}{4}\)
\(\frac{12}{18}\)
\(-\frac{168}{192}\)
- תשובה
-
\(-\frac{7}{8}\)
\(-\frac{140}{224}\)
\(\frac{11 x}{11 y}\)
- תשובה
-
\(\frac{x}{y}\)
\(\frac{15 a}{15 b}\)
הכפל שברים
בתרגילים הבאים, הכפל.
\(\frac{2}{5} \cdot \frac{1}{3}\)
- תשובה
-
\(\frac{2}{15}\)
\(\frac{1}{2} \cdot \frac{3}{8}\)
\(\frac{7}{12}\left(-\frac{8}{21}\right)\)
- תשובה
-
\(-\frac{2}{9}\)
\(\frac{5}{12}\left(-\frac{8}{15}\right)\)
\(-28 p\left(-\frac{1}{4}\right)\)
- תשובה
-
7p
\(-51 q\left(-\frac{1}{3}\right)\)
\(\frac{14}{5}(-15)\)
- תשובה
-
-42
\(-1\left(-\frac{3}{8}\right)\)
מחלקים שברים
בתרגילים הבאים, לחלק
\(\frac{1}{2} \div \frac{1}{4}\)
- תשובה
-
2
\(\frac{1}{2} \div \frac{1}{8}\)
\(-\frac{4}{5} \div \frac{4}{7}\)
- תשובה
-
\(-\frac{7}{5}\)
\(-\frac{3}{4} \div \frac{3}{5}\)
\(\frac{5}{8} \div \frac{a}{10}\)
- תשובה
-
\(\frac{25}{4 a}\)
\(\frac{5}{6} \div \frac{c}{15}\)
\(\frac{7 p}{12} \div \frac{21 p}{8}\)
- תשובה
-
\(\frac{2}{9}\)
\(\frac{5 q}{12} \div \frac{15 q}{8}\)
\(\frac{2}{5} \div(-10)\)
- תשובה
-
\(-\frac{1}{25}\)
\(-18 \div-\left(\frac{9}{2}\right)\)
בתרגילים הבאים, לפשט.
\(\frac{\frac{2}{3}}{\frac{8}{9}}\)
- תשובה
-
\(\frac{3}{4}\)
\(\frac{\frac{4}{5}}{\frac{8}{15}}\)
\(\frac{-\frac{9}{10}}{3}\)
- תשובה
-
\(-\frac{3}{10}\)
\(\frac{2}{\frac{5}{8}}\)
\(\frac{\frac{r}{5}}{\frac{s}{3}}\)
- תשובה
-
\(\frac{3 r}{5 s}\)
\(\frac{-\frac{x}{6}}{-\frac{8}{9}}\)
פשט ביטויים שנכתבו באמצעות סרגל שבר
בתרגילים הבאים, לפשט.
\(\frac{4+11}{8}\)
- תשובה
-
\(\frac{15}{8}\)
\(\frac{9+3}{7}\)
\(\frac{30}{7-12}\)
- תשובה
-
-6
\(\frac{15}{4-9}\)
\(\frac{22-14}{19-13}\)
- תשובה
-
\(\frac{4}{3}\)
\(\frac{15+9}{18+12}\)
\(\frac{5 \cdot 8}{-10}\)
- תשובה
-
-4
\(\frac{3 \cdot 4}{-24}\)
\(\frac{15 \cdot 5-5^{2}}{2 \cdot 10}\)
- תשובה
-
\(\frac{5}{2}\)
\(\frac{12 \cdot 9-3^{2}}{3 \cdot 18}\)
\(\frac{2+4(3)}{-3-2^{2}}\)
- תשובה
-
-2
\(\frac{7+3(5)}{-2-3^{2}}\)
תרגם ביטויים לביטויים עם שברים
בתרגילים הבאים, תרגם כל ביטוי באנגלית לביטוי אלגברי.
המנה של c והסכום של d ו- 9.
- תשובה
-
\(\frac{c}{d+9}\)
המנה של ההבדל של h ו- k, ו- -5.
הוסף וחיסור שברים
הוסף וחיסור שברים עם מכנה משותף
בתרגילים הבאים, הוסף.
\(\frac{4}{9}+\frac{1}{9}\)
- תשובה
-
\(\frac{5}{9}\)
\(\frac{2}{9}+\frac{5}{9}\)
\(\frac{y}{3}+\frac{2}{3}\)
- תשובה
-
\(\frac{y+2}{3}\)
\(\frac{7}{p}+\frac{9}{p}\)
\(-\frac{1}{8}+\left(-\frac{3}{8}\right)\)
- תשובה
-
\(-\frac{1}{2}\)
\(-\frac{1}{8}+\left(-\frac{5}{8}\right)\)
בתרגילים הבאים, לחסר.
\(\frac{4}{5}-\frac{1}{5}\)
- תשובה
-
\(\frac{3}{5}\)
\(\frac{4}{5}-\frac{3}{5}\)
\(\frac{y}{17}-\frac{9}{17}\)
- תשובה
-
\(\frac{y-9}{17}\)
\(\frac{x}{19}-\frac{8}{19}\)
\(-\frac{8}{d}-\frac{3}{d}\)
- תשובה
-
\(-\frac{11}{d}\)
\(-\frac{7}{c}-\frac{7}{c}\)
הוסף או חיסור שברים עם מכנים שונים
בתרגילים הבאים, להוסיף או לחסר.
\(\frac{1}{3}+\frac{1}{5}\)
- תשובה
-
\(\frac{8}{15}\)
\(\frac{1}{4}+\frac{1}{5}\)
\(\frac{1}{5}-\left(-\frac{1}{10}\right)\)
- תשובה
-
\(\frac{3}{10}\)
\(\frac{1}{2}-\left(-\frac{1}{6}\right)\)
\(\frac{2}{3}+\frac{3}{4}\)
- תשובה
-
\(\frac{17}{12}\)
\(\frac{3}{4}+\frac{2}{5}\)
\(\frac{11}{12}-\frac{3}{8}\)
- תשובה
-
\(\frac{13}{24}\)
\(\frac{5}{8}-\frac{7}{12}\)
\(-\frac{9}{16}-\left(-\frac{4}{5}\right)\)
- תשובה
-
\(\frac{19}{80}\)
\(-\frac{7}{20}-\left(-\frac{5}{8}\right)\)
\(1+\frac{5}{6}\)
- תשובה
-
\(\frac{11}{6}\)
\(1-\frac{5}{9}\)
השתמש בסדר הפעולות כדי לפשט שברים מורכבים
בתרגילים הבאים, לפשט.
\(\frac{\left(\frac{1}{5}\right)^{2}}{2+3^{2}}\)
- תשובה
-
\(\frac{1}{275}\)
\(\frac{\left(\frac{1}{3}\right)^{2}}{5+2^{2}}\)
\(\frac{\frac{2}{3}+\frac{1}{2}}{\frac{3}{4}-\frac{2}{3}}\)
- תשובה
-
14
\(\frac{\frac{3}{4}+\frac{1}{2}}{\frac{5}{6}-\frac{2}{3}}\)
הערך ביטויים משתנים עם שברים
בתרגילים הבאים, להעריך.
\(x+\frac{1}{2}\)מתי
- \(x=-\frac{1}{8}\)
- \(x=-\frac{1}{2}\)
- תשובה
-
- \(\frac{3}{8}\)
- \(0\)
\(x+\frac{2}{3}\)מתי
- \(x=-\frac{1}{6}\)
- \(x=-\frac{5}{3}\)
4 \(p^{2} q\) מתי \(p=-\frac{1}{2}\) ו \(q=\frac{5}{9}\)
- תשובה
-
\(\frac{5}{9}\)
5 \(m^{2} n\) מתי \(m=-\frac{2}{5}\) ו \(n=\frac{1}{3}\)
\(\frac{u+v}{w}\)מתי
\(u=-4, v=-8, w=2\)
- תשובה
-
-6
\(\frac{m+n}{p}\)מתי
\(m=-6, n=-2, p=4\)
עשרוניות
שם וכתיבה עשרוניות
בתרגילים הבאים, כתוב כעשרוני.
שמונה ושלוש מאיות
- תשובה
-
8.03
תשע ושבע מאיות
אלפית
- תשובה
-
0.001
תשעת אלפים
בתרגילים הבאים, שם כל עשרוני.
7.8
- תשובה
-
שבע ושמונה עשיריות
5.01
0.005
- תשובה
-
חמשת אלפים
0.381
עשרוניות עגולות
בתרגילים הבאים, עגול כל מספר עד הקרוב
- המאה
- עשירי
- מספר שלם.
5.7932
- תשובה
-
- 5.79
- 5.8
- 6
3.6284
12.4768
- תשובה
-
- 12.48
- 12.5
- 12
25.8449
הוספה וחיסור עשרוניות
בתרגילים הבאים, להוסיף או לחסר.
18.37+9.36
- תשובה
-
27.73
256.37—85.49
15.35—20.88
- תשובה
-
-5.53
37.5 +12.23
-4.2+ (-9.3)
- תשובה
-
-13.5
-8.6+ (-8.6)
100—64.2
- תשובה
-
35.8
100—65.83
2.51+40
- תשובה
-
42.51
9.38+60
להכפיל ולחלק עשרונים
בתרגילים הבאים, הכפל.
(0.3) (0.4)
- תשובה
-
0.12
(0.6) (0.7)
(8.52) (3.14)
- תשובה
-
26.7528
(5.32) (4.86)
(0.09) (24.78)
- תשובה
-
2.2302
(0.04) (36.89)
בתרגילים הבאים, לחלק.
\(0.15 \div 5\)
- תשובה
-
0.03
\(0.27 \div 3\)
\(\$ 8.49 \div 12\)
- תשובה
-
$0.71
\(\$ 16.99 \div 9\)
\(12 \div 0.08\)
- תשובה
-
150
\(5 \div 0.04\)
המר ספרות עשרוניות, שברים ואחוזים
בתרגילים הבאים, כתוב כל עשרוני כשבר.
0.08
- תשובה
-
\(\frac{2}{25}\)
0.17
0.425
- תשובה
-
\(\frac{17}{40}\)
0.184
1.75
- תשובה
-
\(\frac{7}{4}\)
0.035
בתרגילים הבאים, המירו כל שבר לעשרוני.
\(\frac{2}{5}\)
- תשובה
-
0.4
\(\frac{4}{5}\)
\(-\frac{3}{8}\)
- תשובה
-
−0.375
\(-\frac{5}{8}\)
\(\frac{5}{9}\)
- תשובה
-
\(0 . \overline{5}\)
\(\frac{2}{9}\)
\(\frac{1}{2}+6.5\)
- תשובה
-
7
\(\frac{1}{4}+10.75\)
בתרגילים הבאים, המירו כל אחוז לעשרוני.
5%
- תשובה
-
0.05
9%
40%
- תשובה
-
0.4
50%
115%
- תשובה
-
1.15
125%
בתרגילים הבאים, המירו כל עשרוני לאחוז.
0.18
- תשובה
-
18%
0.15
0.009
- תשובה
-
0.9%
0.008
1.5
- תשובה
-
150%
2.2
המספרים האמיתיים
פשט ביטויים עם שורשים מרובעים
בתרגילים הבאים, לפשט.
\(\sqrt{64}\)
- תשובה
-
8
\(\sqrt{144}\)
\(-\sqrt{25}\)
- תשובה
-
-5
\(-\sqrt{81}\)
זיהוי מספרים שלמים, מספרים רציונליים, מספרים לא רציונליים ומספרים ממשיים
בתרגילים הבאים, כתוב כיחס בין שני מספרים שלמים.
- 9
- 8.47
- תשובה
-
- \(\frac{9}{1}\)
- \(\frac{847}{100}\)
- -15
- 3.591
בתרגילים הבאים, רשום את
- מספרים רציונליים,
- מספרים לא רציונליים.
\(0.84,0.79132 \ldots, 1 . \overline{3}\)
- תשובה
-
- \(0.84,1.3\)
- \(0.79132 \ldots\)
\(2.3 \overline{8}, 0.572,4.93814 \ldots\)
בתרגילים הבאים, זהה אם כל מספר הוא רציונלי או לא הגיוני.
- \(\sqrt{121}\)
- \(\sqrt{48}\)
- תשובה
-
- הגיוני
- לא הגיוני
- \(\sqrt{56}\)
- \(\sqrt{16}\)
בתרגילים הבאים, זהה אם כל מספר הוא מספר אמיתי או לא מספר אמיתי.
- \(\sqrt{-9}\)
- \(-\sqrt{169}\)
- תשובה
-
- לא מספר אמיתי
- מספר אמיתי
- \(\sqrt{-64}\)
- \(-\sqrt{81}\)
בתרגילים הבאים, רשום את
- מספרים שלמים,
- מספרים שלמים,
- מספרים רציונליים,
- מספרים לא רציונליים,
- מספרים ממשיים עבור כל קבוצה של מספרים.
\(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
- תשובה
-
- \(0, \sqrt{16}\)
- \(-4,0, \sqrt{16}\)
- \(-4,0, \frac{5}{6}, \sqrt{16}\)
- \(\sqrt{18}, 5.2537 \ldots\)
- \(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
\(-\sqrt{4}, 0 . \overline{36}, \frac{13}{3}, 6.9152 \ldots, \sqrt{48}, 10 \frac{1}{2}\)
אתר שברים בשורת המספרים
בתרגילים הבאים, אתר את המספרים בשורת מספרים.
\(\frac{2}{3}, \frac{5}{4}, \frac{12}{5}\)
- תשובה
-
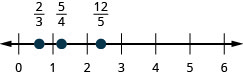
\(\frac{1}{3}, \frac{7}{4}, \frac{13}{5}\)
\(2 \frac{1}{3},-2 \frac{1}{3}\)
- תשובה
-
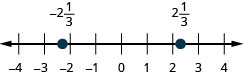
\(1 \frac{3}{5},-1 \frac{3}{5}\)
בתרגילים הבאים, סדר כל אחד מזוגות המספרים הבאים, באמצעות < or >.
−1___ \(-\frac{1}{8}\)
- תשובה
-
<
\(-3 \frac{1}{4}\)___−4
\(-\frac{7}{9}\)___ \(\frac{4}{9}\)
- תשובה
-
>
\(-2\)___ \(\frac{19}{8}\)
אתר ספרות עשרוניות בשורת המספרים
בתרגילים הבאים, אתר בשורת המספרים.
0.3
- תשובה
-
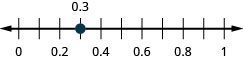
-0.2
-2.5
- תשובה
-
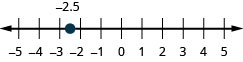
2.7
בתרגילים הבאים, סדר כל אחד מזוגות המספרים הבאים, באמצעות < or >.
0.9___0.6
- תשובה
-
>
0.7___0.8
-0.6___−0.59
- תשובה
-
>
-0.27___−0.3
מאפיינים של מספרים ממשיים
השתמש בתכונות הקומוטטיביות והאסוציאטיביות
בתרגילים הבאים, השתמש בנכס האסוציאטיבי כדי לפשט.
-12 (4 מ ')
- תשובה
-
−48 מ '
30 \(\left(\frac{5}{6} q\right)\)
(א+16) +31
- תשובה
-
a+47
(ג+0.2) +0.7
בתרגילים הבאים, לפשט.
6y+37+ (-6 שנים)
- תשובה
-
37
\(\frac{1}{4}+\frac{11}{15}+\left(-\frac{1}{4}\right)\)
\(\frac{14}{11} \cdot \frac{35}{9} \cdot \frac{14}{11}\)
- תשובה
-
\(\frac{35}{9}\)
\(-18 \cdot 15 \cdot \frac{2}{9}\)
\(\left(\frac{7}{12}+\frac{4}{5}\right)+\frac{1}{5}\)
- תשובה
-
1 \(\frac{7}{12}\)
(3.98 ד+0.75 ד) +1.25 ד
11 איקס+8 ים+16 איקס+15 שנה
- תשובה
-
27 איקס+23 שנה
52 מ+ (-20 נ) + (-18 מ') + (-5 נ)
השתמש בזהות ובמאפיינים ההפוכים של תוספת וכפל
בתרגילים הבאים, מצא את ההיפוך התוסף של כל מספר.
- \(\frac{1}{3}\)
- 5.1
- \(-14\)
- \(-\frac{8}{5}\)
- תשובה
-
- \(-\frac{1}{3}\)
- \(-5.1\)
- -14
- \(-\frac{8}{5}\)
- \(-\frac{7}{8}\)
- \(-0.03\)
- 17
- \(\frac{12}{5}\)
בתרגילים הבאים, מצא את ההופכי הכפול של כל מספר.
- \(10\)
- \(-\frac{4}{9}\)
- 0.6
- תשובה
-
- \(\frac{1}{10}\)
- \(-\frac{9}{4}\)
- \(\frac{5}{3}\)
- \(-\frac{9}{2}\)
- -7
- 2.1
השתמש במאפיינים של אפס
בתרגילים הבאים, לפשט.
83 \(\cdot 0\)
- תשובה
-
0
\(\frac{0}{9}\)
\(\frac{5}{0}\)
- תשובה
-
לא מוגדר
\(0 \div \frac{2}{3}\)
בתרגילים הבאים, לפשט.
43+39+ (-43)
- תשובה
-
39
(נ+6.75) +0.25
\(\frac{5}{13} \cdot 57 \cdot \frac{13}{5}\)
- תשובה
-
57
\(\frac{1}{6} \cdot 17 \cdot 12\)
\(\frac{2}{3} \cdot 28 \cdot \frac{3}{7}\)
- תשובה
-
8
\(9(6 x-11)+15\)
פשט ביטויים באמצעות המאפיין החלוקתי
בתרגילים הבאים, פשט את השימוש בנכס החלוקה.
7 (x+9)
- תשובה
-
7x+63
9 (u−4)
-3 (6 מ '-1)
- תשובה
-
-18 מ '+3
-8 (−7א −12)
\(\frac{1}{3}(15 n-6)\)
- תשובה
-
5n-2
\((y+10) \cdot p\)
(א-4) − (6a+9)
- תשובה
-
−5א −13
4 (איקס+3) -8 (איקס-7)
מערכות מדידה
1.1 הגדירו יחידות מדידה אמריקאיות והמירו מיחידה אחת לאחרת
בתרגילים הבאים, להמיר את היחידות. סיבוב לעשירית הקרובה ביותר.
סוכת פרחונית בגובה 7 מטר. המר את הגובה לאינצ'ים.
- תשובה
-
84 סנטימטרים
מסגרת תמונה היא 42 אינץ 'רוחב. המר את הרוחב לרגליים.
קלי בגובה 5 רגל 4 אינץ'. המר את הגובה שלה לסנטימטרים.
- תשובה
-
64 סנטימטרים
מגרש משחקים הוא ברוחב 45 רגל. המר את הרוחב לחצרות.
גובהו של הר שאסטה הוא 14,179 רגל. המר את הגובה למיילים.
- תשובה
-
2.7 מיילים
שאמו שוקל 4.5 טון. המר את המשקל לקילוגרמים.
המחזה נמשך \(1\frac{3}{4}\) שעות. המר את הזמן לדקות.
- תשובה
-
105 דקות
כמה כפות יש ברבע?
התינוק של נעמי שקל 5 קילו 14 אונקיות בלידה. המר את המשקל לאונקיות.
- תשובה
-
94 אונקיות
טרין צריכה 30 כוסות צבע לפרויקט האמנות הכיתתי שלה. המר את עוצמת הקול לגלונים.
השתמש ביחידות מדידה מעורבות במערכת האמריקאית.
בתרגילים הבאים, לפתור.
ג'ון תפס 4 לובסטרים. משקולות הלובסטרים היו 1 קילו 9 אונקיות, 1 קילו 12 אונקיות, 4 פאונד 2 אונקיות ו -2 פאונד 15 אונקיות. מה היה המשקל הכולל של הלובסטרים?
- תשובה
-
10 פאונד. 6 עוז.
בכל יום בשבוע שעבר רשם פדרו את מספר הדקות שבילה בקריאה. מספר הדקות היה 50, 25, 83, 45, 32, 60, 135. כמה שעות בילה פדרו בקריאה?
גובהו של פואד הוא 6 רגל 2 אינץ'. אם הוא עומד על שלב של סולם בגובה 8 רגל 10 סנטימטרים, כמה גבוה מעל הקרקע הוא החלק העליון של ראשו של פואד?
- תשובה
-
15 רגל
דלילה רוצה להכין כיסויי כרית לזרוק. כל כיסוי לוקח 30 אינץ 'של בד. כמה מטרים של בד היא צריכה עבור 4 כיסויים?
בצע המרות יחידות במערכת המטרית
בתרגילים הבאים, להמיר את היחידות.
דונה גובהה 1.7 מטר. המר את גובהה לסנטימטרים.
- תשובה
-
170 סנטימטרים
הר האוורסט גובהו 8,850 מטר. המר את הגובה לקילומטרים.
כוס יוגורט אחת מכילה 488 מיליגרם סידן. המר את זה לגרמים.
- תשובה
-
0.488 גרם
כוס יוגורט אחת מכילה 13 גרם חלבון. המירו את זה למיליגרם.
סרחיו שקל 2.9 קילוגרם בלידתו. המר את זה לגרמים.
- תשובה
-
2,900 גרם
בקבוק מים הכיל 650 מיליליטר. המר את זה לליטר.
השתמש ביחידות מדידה מעורבות במערכת המטרית
במאמצים הבאים, לפתור.
גובה מין הוא 2 מטר. גובהו של בתו 88 סנטימטרים. כמה גבוה יותר מין מבתו?
- תשובה
-
1.12 מטר
לסלמה היה בקבוק מים של 1 ליטר. אם היא שתתה 145 מיליליטר, כמה מים נותרו בבקבוק?
מנה אחת של מיץ חמוציות מכיל 30 גרם סוכר. כמה קילוגרמים של סוכר נמצאים 30 מנות של מיץ חמוציות?
- תשובה
-
0.9 קילוגרם
גרם טופו אחד סיפק 2 גרם חלבון. כמה מיליגרם חלבון מסופקים על ידי 5 אונקיות טופו?
המר בין ארה"ב למערכות המדידה המטריות
בתרגילים הבאים, בצע את המרות היחידה. סיבוב לעשירית הקרובה ביותר.
מג'יד גובהו 69 סנטימטרים. המר את גובהו לסנטימטרים.
- תשובה
-
175.3 סנטימטרים
אורכו של מגרש כדורסל במכללה הוא 84 רגל. המר אורך זה למטר.
קרוליין הלכה 2.5 ק"מ. המר אורך זה למיילים.
- תשובה
-
1.6 מיילים
לוקאס שוקל 78 ק"ג. המר את משקלו לקילוגרמים.
המכונית של סטיב מחזיקה 55 ליטר גז. המירו את זה לגלונים.
- תשובה
-
14.6 גלונים
קופסת ספרים שוקלת 25 פאונד. המר את המשקל לקילוגרמים.
המר בין טמפרטורות פרנהייט לצלזיוס
בתרגילים הבאים, המירו את טמפרטורות פרנהייט למעלות צלזיוס. סיבוב לעשירית הקרובה ביותר.
95 מעלות פרנהייט
- תשובה
-
35 מעלות צלזיוס
23 מעלות פרנהייט
20° פרנהייט
- תשובה
-
-6.7 מעלות צלזיוס
64 מעלות פרנהייט
בתרגילים הבאים, המירו את טמפרטורות צלזיוס למעלות פרנהייט. סיבוב לעשירית הקרובה ביותר.
30 מעלות צלזיוס
- תשובה
-
86 מעלות צלזיוס
—5 מעלות צלזיוס
—12 מעלות צלזיוס
- תשובה
-
10.4 מעלות צלזיוס
24 מעלות צלזיוס
מבחן תרגול פרק
כתוב כמספר שלם באמצעות ספרות: מאתיים וחמש אלף, שש מאות שבע עשרה.
- תשובה
-
205,617
מצא את הפקטוריזציה העיקרית של 504.
מצא את הכפולה הפחות נפוצה של 18 ו -24.
- תשובה
-
72
שלב מונחים דומים: 5n+8+2n−1.
בתרגילים הבאים, להעריך.
\(-|x|\)מתי \(x=-2\)
- תשובה
-
-2
11−א כאשר א=−3
תרגם לביטוי אלגברי ופשט: עשרים פחות משליליים 7.
- תשובה
-
-7-20; -27
למוניק יש יתרה של -18 דולר בחשבון העובר ושב שלה. היא מפקידה 152 דולר לחשבון. מהו האיזון החדש?
סיבוב 677.1348 למאה הקרובה ביותר.
- תשובה
-
677.13
המר \(\frac{4}{5}\) לעשרוני.
המר 1.85 לאחוז.
- תשובה
-
185%
אתר \(\frac{2}{3},-1.5,\) \(\frac{9}{4}\) ועל שורת מספר.
בתרגילים הבאים, לפשט כל ביטוי.
\(4+10(3+9)-5^{2}\)
- תשובה
-
99
-85+42
-19—25
- תשובה
-
-44
\((-2)^{4}\)
\(-5(-9) \div 15\)
- תשובה
-
3
\(\frac{3}{8} \cdot \frac{11}{12}\)
\(\frac{4}{5} \div \frac{9}{20}\)
- תשובה
-
\(\frac{16}{9}\)
\(\frac{12+3 \cdot 5}{15-6}\)
\(\frac{m}{7}+\frac{10}{7}\)
- תשובה
-
\(\frac{m+10}{7}\)
\(\frac{7}{12}-\frac{3}{8}\)
\(-5.8+(-4.7)\)
- תשובה
-
-10.5
100—64.25
(0.07) (31.95)
- תשובה
-
2.2365
\(9 \div 0.05\)
\(-14\left(\frac{5}{7} p\right)\)
- תשובה
-
−10p
(u+8) -9
6x+ (-4 שנים) +9x+8 שנים
- תשובה
-
15x+4 שנים
\(\frac{0}{23}\)
\(\frac{75}{0}\)
- תשובה
-
לא מוגדר
-2 (13 ש-5)
סרט נמשך \(\frac{2}{3}\) שעה אחת. כמה דקות זה נמשך? (1 שעה \(=60\) דקות)
- תשובה
-
100 דקות
גובה רכב השטח של מייק הוא 5 רגל 11 אינץ '. הוא רוצה לשים תיק מטען על הגג על רכב השטח. גובה תיק המטען הוא 1 רגל 6 אינץ'. מה יהיה הגובה הכולל של רכב השטח עם תיק המטען על הגג? (רגל אחת = 12 אינץ ')
ג'ניפר רצה 2.8 קילומטרים. המר אורך זה לקילומטרים. (מייל אחד = 1.61 ק"מ)
- תשובה
-
ק"מ4.508


