1.7: הוסף וחסר שברים
- Page ID
- 205627
בסוף פרק זה תוכל:
- הוסף או חיסור שברים עם מכנה משותף
- הוסף או חיסור שברים עם מכנים שונים
- השתמש בסדר הפעולות כדי לפשט שברים מורכבים
- הערך ביטויים משתנים עם שברים
מבוא יסודי יותר לנושאים המכוסים בחלק זה ניתן למצוא בפרק Prealgebra, שברים.
הוספה או הפחתה של שברים עם מכנה משותף
כשהכפלנו שברים, פשוט הכפלנו את המספרים והכפלנו את המכנים ישר לרוחב. כדי להוסיף או לחסר שברים, עליהם להיות מכנה משותף.
אם\(a,b\), \(c\) והם מספרים איפה\(c\neq 0\), אז
\[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c} \quad \text{and} \quad \dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a - b}{c}\]
כדי להוסיף או לחסר שברים, הוסף או גרע את המספרים והנח את התוצאה על המכנה המשותף.
ביצוע פעילויות המתמטיקה המניפולטיבית "תוספת שבר מודל" ו"חיסור שברי מודל "יעזור לך לפתח הבנה טובה יותר של הוספה וחיסור של שברים.
מצא את הסכום:\(\dfrac{x}{3} + \dfrac{2}{3}\).
- תשובה
-
\[\begin{array} {ll} {} &{\dfrac{x}{3} + \dfrac{2}{3}} \\ {\text{Add the numerators and place the sum over the common denominator}} &{\dfrac{x + 2}{3}} \end{array}\]
מצא את הסכום:\(\dfrac{x}{4} + \dfrac{3}{4}\).
- תשובה
-
\(\dfrac{x + 3}{4}\)
מצא את הסכום:\(\dfrac{y}{8} + \dfrac{5}{8}\).
- תשובה
-
\(\dfrac{y + 5}{8}\)
מצא את ההבדל: \(-\dfrac{23}{24} - \dfrac{13}{24}\)
- תשובה
-
\[\begin{array} {ll} {} &{-\dfrac{23}{24} - \dfrac{13}{24}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-23 - 13}{24}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Simplify.}} &{\dfrac{-36}{24}} \\ {\text{Simplify. Remember, }-\dfrac{a}{b} = \dfrac{-a}{b}} &{-\dfrac{3}{2}} \end{array}\]
מצא את ההבדל: \(-\dfrac{19}{28} - \dfrac{7}{28}\)
- תשובה
-
\(-\dfrac{26}{28}\)
מצא את ההבדל: \(-\dfrac{27}{32} - \dfrac{1}{32}\)
- תשובה
-
\(-\dfrac{7}{8}\)
מצא את ההבדל: \(-\dfrac{10}{x} - \dfrac{4}{x}\)
- תשובה
-
\[\begin{array} {ll} {} &{-\dfrac{10}{x} - \dfrac{4}{x}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-14}{x}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Rewrite with the sign in front of the fraction.}} &{-\dfrac{14}{x}} \end{array}\]
מצא את ההבדל: \(-\dfrac{9}{x} - \dfrac{7}{x}\)
- תשובה
-
\(-\dfrac{16}{x}\)
מצא את ההבדל: \(-\dfrac{17}{a} - \dfrac{5}{a}\)
- תשובה
-
\(-\dfrac{22}{a}\)
פשט: \(\dfrac{3}{8} + (-\dfrac{5}{8}) - \dfrac{1}{8}\)
- תשובה
-
\[\begin{array} {ll} {\text{Add and Subtract fractions — do they have a }} &{\frac{3}{8} + (-\frac{5}{8}) - \frac{1}{8}} \\ {\text{common denominator? Yes.}} &{} \\ {\text{Add and subtract the numerators and place }} &{\frac{3 + (-5) - 1}{8}} \\ {\text{the result over the common denominator.}} &{} \\ {\text{Simplify left to right.}} &{\frac{-2 - 1}{8}} \\ {\text{Simplify.}} &{-\frac{3}{8}} \end{array}\]
פשט: \(\dfrac{2}{9} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)
- תשובה
-
\(-1\)
פשט: \(\dfrac{2}{5} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)
- תשובה
-
\(-\dfrac{2}{3}\)
הוסף או חיסור שברים עם מכנים שונים
כפי שראינו, כדי להוסיף או לחסר שברים, המכנים שלהם חייבים להיות זהים. המכנה הפחות משותף (LCD) של שני שברים הוא המספר הקטן ביותר שיכול לשמש כמכנה משותף לשברים. ה- LCD של שני השברים הוא הכפולה הפחות נפוצה (LCM) של המכנים שלהם.
המכנה הפחות משותף (LCD) של שני שברים הוא הכפולה הפחות משותפת (LCM) של המכנים שלהם.
ביצוע פעילות המתמטיקה המניפולטיבית "מציאת המכנה הפחות משותף" יעזור לך לפתח הבנה טובה יותר של ה- LCD.
לאחר שנמצא את המכנה הפחות משותף לשני שברים, אנו ממירים את השברים לשברים שווים עם ה- LCD. חיבור שלבים אלה מאפשר לנו להוסיף ולחסר שברים מכיוון שהמכנים שלהם יהיו זהים!
הוסף: \(\dfrac{7}{12} + \dfrac{5}{18}\)
- תשובה
-



הוסף: \(\dfrac{7}{12} + \dfrac{11}{15}\)
- תשובה
-
\(\dfrac{79}{60}\)
הוסף: \(\dfrac{7}{12} + \dfrac{11}{15}\)
- תשובה
-
\(\dfrac{103}{60}\)
- האם יש להם מכנה משותף?
- כן - עבור לשלב 2.
- לא - כתוב מחדש כל שבר עם ה- LCD (המכנה המשותף לפחות). מצא את ה- LCD. שנה כל שבר לשבר שווה ערך עם ה- LCD כמכנה שלו.
- הוסף או הפחת את השברים.
- פשט, אם אפשר.
כאשר מוצאים את השברים המקבילים הדרושים ליצירת המכנים המשותפים, יש דרך מהירה למצוא את המספר הדרוש לנו בכדי להכפיל גם את המונה וגם את המכנה. שיטה זו עובדת אם מצאנו את ה- LCD על ידי פקטורינג לפרימים ראשוניים.
תסתכל על הגורמים של LCD ולאחר מכן בכל עמודה מעל גורמים אלה. הגורמים ה"חסרים "של כל מכנה הם המספרים הדרושים לנו.

בתרגיל\(\PageIndex{13}\), ל- LCD, 36, יש שני גורמים של 2 ושני גורמים של 3.
למונה 12 שני גורמים של 2 אך רק אחד מתוך 3 - כך שהוא "חסר" אחד 3 - אנו מכפילים את המונה והמכנה ב -3.
למונה 18 חסר גורם אחד של 2 - אז נכפיל את המונה והמכנה ב -2.
אנו נשתמש בשיטה זו כאשר אנו מחסירים את השברים בתרגיל\(\PageIndex{16}\).
חיסור: \(\dfrac{7}{15} - \dfrac{19}{24}\)
- תשובה
-
האם לשברים יש מכנה משותף? לא, אז אנחנו צריכים למצוא את LCD.
מצא את ה- LCD. 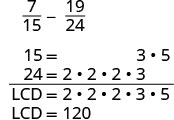
שימו לב, 15 "חסרים" שלושה גורמים של 2 ו -24 "חסרים" את ה- 5 מגורמי ה- LCD. אז אנו מכפילים 8 בשבר הראשון ו -5 בשבר השני כדי לקבל את ה- LCD. כתוב מחדש כשברים שווים עם ה- LCD. 
לפשט. 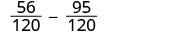
לחסר. \(-\dfrac{39}{120}\) בדוק אם ניתן לפשט את התשובה. \(-\dfrac{13\cdot3}{40\cdot3}\) גם 39 וגם 120 יש גורם של 3. לפשט. \(-\dfrac{13}{40}\) אל תפשט את השברים המקבילים! אם תעשה זאת, תחזור לשברים המקוריים ותאבד את המכנה המשותף!
חיסור: \(\dfrac{13}{24} - \dfrac{17}{32}\)
- תשובה
-
\(\dfrac{1}{96}\)
חיסור: \(\dfrac{7}{15} - \dfrac{19}{24}\)
- תשובה
-
\(\dfrac{75}{224}\)
בדוגמה הבאה, לאחד השברים יש משתנה במונה שלו. שימו לב שאנחנו עושים את אותם השלבים כמו כאשר שני המספרים הם מספרים.
הוסף: \(\dfrac{3}{5} + \dfrac{x}{8}\)
- תשובה
-
לשברים יש מכנים שונים.
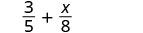
מצא את ה- LCD. 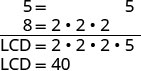
כתוב מחדש כשברים שווים עם ה- LCD. 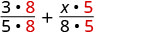
לפשט. 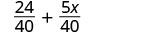
להוסיף. 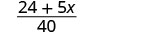
זכור, אנו יכולים להוסיף רק מונחים דומים: \(24\) \(5x\) ואינם דומים למונחים.
הוסף: \(\dfrac{y}{6} + \dfrac{7}{9}\)
- תשובה
-
\(\dfrac{3y + 14}{18}\)
הוסף: \(\dfrac{x}{6} + \dfrac{7}{15}\)
- תשובה
-
\(\dfrac{15x + 42}{153}\)
כעת יש לנו את כל ארבע הפעולות לשברים. הטבלה \(\PageIndex{1}\) מסכמת את פעולות השבר.
| כפל שברים | חטיבת שבר |
| \(\dfrac{a}{b}\cdot \dfrac{c}{d} = \dfrac{ac}{bd}\) הכפל את המספרים והכפיל את המכנים |
\(\dfrac{a}{b}\div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\) הכפל את השבר הראשון בהדדיות של השני. |
| תוספת שבר | חיסור שבר |
| \(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\) הוסף את המספרים והנח את הסכום מעל המכנה המשותף. |
\(\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a - b}{c}\) הפחת את המספרים והנח את ההפרש על המכנה המשותף. |
| כדי להכפיל או לחלק שברים, ו- LCD אינו נחוץ. כדי להוסיף או לחסר שברים, יש צורך ב- LCD. | |
פשט:
- \(\dfrac{5x}{6} - \dfrac{3}{10}\)
- \(\dfrac{5x}{6}\cdot \dfrac{3}{10}\).
- תשובה
-
ראשית שאל, "מהו הניתוח?" ברגע שנזהה את הפעולה שתקבע אם אנו זקוקים למכנה משותף. זכרו, אנו זקוקים למכנה משותף כדי להוסיף או לחסר, אך לא להכפיל או לחלק.
1. מהו המבצע? הפעולה היא חיסור.
\[\begin{array} {ll} {\text{Do the fractions have a common denominator? No.}} &{\frac{5x}{6} - \frac{3}{10}} \\ {\text{Rewrite each fractions as an equivalent fraction with the LCD.}} &{\frac{5x\cdot 5}{6\cdot 5} - \frac{3\cdot3}{10\cdot3}} \\ {} &{\frac{25x}{30} - \frac{9}{30}} \\{\text{Subtract the numerators and place the difference over the}} &{\frac{25x - 9}{30}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify, if possible. There are no common factors.}} &{} \\ {\text{The fraction is simplified.}} &{} \end{array}\]
2. מהו המבצע? כפל.
\[\begin{array} {ll} {} &{\frac{5x}{6}\cdot \frac{3}{10}} \\ {\text{To multiply fractions, multiply the numerators and multiply}} &{\frac{5x\cdot 3}{6\cdot 10}} \\ {\text{the denominators}} &{} \\{\text{Rewrite, showing common factors.}} &{\frac{\not 5 x\cdot\not3}{2\cdot\not3\cdot2\cdot\not5}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify.}} &{\frac{x}{4}} \end{array}\]
פשט:
- \(\dfrac{3a}{4} - \dfrac{8}{9}\)
- \(\dfrac{3a}{4}\cdot\dfrac{8}{9}\)
- תשובה
-
- \(\dfrac{27a - 32}{36}\)
- \(\dfrac{2a}{3}\)
פשט:
- \(\dfrac{4k}{5} - \dfrac{1}{6}\)
- \(\dfrac{4k}{5}\cdot\dfrac{1}{6}\)
- תשובה
-
- \(\dfrac{24k - 5}{30}\)
- \(\dfrac{2k}{15}\)
השתמש בסדר הפעולות כדי לפשט שברים מורכבים
ראינו ששבר מורכב הוא שבר בו המספר או המכנה מכיל שבר. סרגל השבר מציין חלוקה. פישטנו את השבר המורכב \(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) על ידי חלוקה \(\dfrac{3}{4}\) לפי\(\dfrac{5}{8}\).
כעת נבחן שברים מורכבים שבהם המונה או המכנה מכילים ביטוי שניתן לפשט. אז ראשית עלינו לפשט לחלוטין את המונה והמכנה בנפרד באמצעות סדר הפעולות. לאחר מכן אנו מחלקים את המונה במכנה.
פשט: \(\dfrac{(\frac{1}{2})^{2}}{4 + 3^{2}}\)
- תשובה
-



פשט: \(\dfrac{(\frac{1}{3})^{2}}{2^{3} + 2}\)
- תשובה
-
\(\dfrac{1}{90}\)
פשט: \(\dfrac{1 + 4^{2}}{(\frac{1}{4})^{2}}\)
- תשובה
-
\(272\)
- פשט את המונה.
- פשט את המכנה.
- מחלקים את המונה על ידי המכנה. פשט במידת האפשר.
פשט: \(\dfrac{\frac{1}{2} + \frac{2}{3}}{\frac{3}{4} - \frac{1}{6}}\)
- תשובה
-
\[\begin{array} {ll} {} &{\frac{(\frac{1}{2} + \frac{2}{3})}{(\frac{3}{4} - \frac{1}{6})}} \\ {\text{Simplify the numerator (LCD = 6) and simplify the denominator (LCD = 12).}} &{\frac{(\frac{3}{6} + \frac{4}{6})}{(\frac{9}{12} - \frac{2}{12})}} \\ {\text{Simplify.}} &{\frac{(\frac{7}{6})}{(\frac{7}{12})}} \\{\text{Divide the numerator by the denominator.}} &{\frac{7}{6}\div\frac{7}{12}} \\ {\text{Simplify.}} &{\frac{7}{6}\cdot\frac{12}{7}} \\ {\text{Divide out common factors.}} &{\frac{7\cdot6\cdot2}{6\cdot7}} \\ {\text{Simplify.}} &{2} \end{array}\]
פשט: \(\dfrac{\frac{1}{3} + \frac{1}{2}}{\frac{3}{4} - \frac{1}{3}}\)
- תשובה
-
\(2\)
פשט: \(\dfrac{\frac{2}{3} - \frac{1}{2}}{\frac{1}{4} + \frac{1}{3}}\)
- תשובה
-
\(\dfrac{2}{7}\)
הערך ביטויים משתנים עם שברים
הערכנו ביטויים בעבר, אך כעת אנו יכולים להעריך ביטויים עם שברים. זכור, כדי להעריך ביטוי, אנו מחליפים את ערך המשתנה בביטוי ואז מפשטים.
להעריך \(x + \dfrac{1}{3}\) מתי
- \(x = -\dfrac{1}{3}\)
- \(x = -\dfrac{3}{4}\)
- תשובה
-
1. כדי להעריך \(x + \dfrac{1}{3}\) מתי\(x = -\dfrac{1}{3}\), \(-\dfrac{1}{3}\) תחליף \(x\) בביטוי.
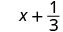
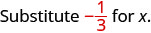
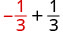
לפשט. \(0\)
2. כדי להעריך \(x + \dfrac{1}{3}\) מתי\(x = -\dfrac{3}{4}\), \(-\dfrac{3}{4}\) תחליף \(x\) בביטוי.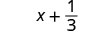

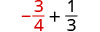
כתוב מחדש כשברים שווים עם ה- LCD, 12. 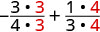
לפשט. 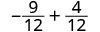
להוסיף. \(-\dfrac{5}{12}\)
להעריך \(x + \dfrac{3}{4}\) מתי
- \(x = -\dfrac{7}{4}\)
- \(x = -\dfrac{5}{4}\)
- תשובה
-
- \(-1\)
- \(-\dfrac{1}{2}\)
להעריך \(y + \dfrac{1}{2}\) מתי
- \(y = \dfrac{2}{3}\)
- \(y = -\dfrac{3}{4}\)
- תשובה
-
- \(\dfrac{7}{6}\)
- \(-\dfrac{1}{12}\)
להעריך \(-\dfrac{5}{6} - y\) מתי \(y = -\dfrac{2}{3}\)
- תשובה
-
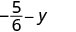
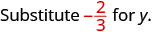
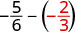
כתוב מחדש כשברים שווים עם ה- LCD,\(6\). 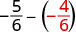
לחסר. 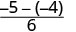
לפשט. \(-\dfrac{1}{6}\)
להעריך \(y + \dfrac{1}{2}\) מתי \(y = \dfrac{2}{3}\)
- תשובה
-
\(-\dfrac{1}{4}\)
להעריך \(y + \dfrac{1}{2}\) מתי \(y = \dfrac{2}{3}\)
- תשובה
-
\(-\dfrac{17}{8}\)
להעריך \(2x^{2}y\) מתי \(x = \dfrac{1}{4}\) ו\(y = -\dfrac{2}{3}\).
- תשובה
-
החלף את הערכים בביטוי.
\(2x^{2}y\) 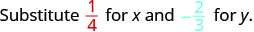
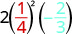
פשט תחילה את המעריכים. \(2(\frac{1}{16})(-\frac{2}{3})\) להכפיל. לחלק את הגורמים המשותפים. שימו לב שאנחנו כותבים \(16\) \(2\cdot2\cdot4\) כדי להקל על ההסרה \(-\frac{\not2\cdot1\cdot\not2}{\not2\cdot\not2\cdot4\cdot3}\) לפשט. \(-\frac{1}{12}\)
להעריך \(3ab^{2}\) מתי \(a = -\dfrac{2}{3}\) ו\(b = -\dfrac{1}{2}\).
- תשובה
-
\(-\dfrac{1}{2}\)
להעריך \(4c^{3}d\) מתי \(c = -\dfrac{1}{2}\) ו\(d = -\dfrac{4}{3}\).
- תשובה
-
\(\dfrac{2}{3}\)
בדוגמה הבאה יהיו רק משתנים, ללא קבועים.
להעריך \(\dfrac{p + q}{r}\) מתי\(p = -4, q = -2\), ו\(r = 8\).
- תשובה
-
כדי להעריך \(\dfrac{p + q}{r}\) מתי\(p = -4, q = -2\), ו\(r = 8\), אנו מחליפים את הערכים בביטוי.
\(\dfrac{p + q}{r}\) 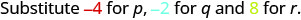
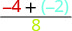
הוסף תחילה את המונה. \(\dfrac{-6}{8}\) לפשט. \(-\dfrac{3}{4}\)
להעריך \(\dfrac{a+b}{c}\) מתי\(a = -8, b = -7\), ו\(c = 6\).
- תשובה
-
\(-\dfrac{5}{2}\)
להעריך \(\dfrac{x+y}{z}\) מתי\(x = 9, y = -18\), ו\(z = -6\).
- תשובה
-
\(\dfrac{3}{2}\)
מושגי מפתח
- חיבור וחיסור שברים: אם\(a, b\), \(c\) והם מספרים היכן\(c\neq 0\), ואז
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\) \(\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}\)
וכדי להוסיף או לחסר שברים, הוסף או גרע את המספרים והניח את התוצאה על המכנה המשותף.
- אסטרטגיה להוספה או חיסור של שברים
- האם יש להם מכנה משותף?
כן - עבור לשלב 2.
לא - כתוב מחדש כל שבר עם ה- LCD (המכנה המשותף לפחות). מצא את ה- LCD. שנה כל שבר לשבר שווה ערך עם ה- LCD כמכנה שלו. - הוסף או הפחת את השברים.
- פשט, אם אפשר. כדי להכפיל או לחלק שברים, אין צורך ב- LCD. כדי להוסיף או לחסר שברים, יש צורך ב- LCD.
- האם יש להם מכנה משותף?
- פשט שברים מורכבים
- פשט את המונה.
- פשט את המכנה.
- מחלקים את המונה על ידי המכנה. פשט במידת האפשר.


