1.2: מבוא למספרים שלמים

מטרות למידה

• בסוף פרק זה תוכל:
• השתמש בערך מקום עם מספרים שלמים
• זהה מכפילים והחל מבחני חלוקה
• מצא פקטוריזציות ראשוניות ומכפילים פחות נפוצים

כאשר אנו מתחילים את לימודי האלגברה היסודית, עלינו לרענן חלק מהכישורים ואוצר המילים שלנו. פרק זה יתמקד במספרים שלמים, מספרים שלמים, שברים, עשרונים ומספרים ממשיים. נתחיל גם בשימוש בסימון ובאוצר מילים אלגברי.

השתמש בערך מקום עם מספרים שלמים

המספרים הבסיסיים ביותר המשמשים באלגברה הם המספרים בהם אנו משתמשים כדי לספור אובייקטים בעולמנו: \(1, 2, 3, 4\) וכן הלאה. אלה נקראים מספר הספירה s. ספירת מספרים נקראת גם מספרים טבעיים. אם נוסיף אפס למספרי הספירה, נקבל את מערך המספרים השלמים.

• ספירת מספרים: \(1, 2, 3, …\)
• מספרים שלמים: \(0, 1, 2, 3, …\)

הסימון "\(…\)" נקרא אליפסה ופירושו "וכן הלאה", או שהתבנית נמשכת בלי סוף.

אנו יכולים לדמיין ספירת מספרים ומספרים שלמים בשורת מספרים (ראה איור\(\PageIndex{1}\)).

איור\(\PageIndex{1}\): המספרים בשורת המספרים גדלים ככל שהם עוברים משמאל לימין, וקטנים ככל שהם עוברים מימין לשמאל. בעוד ששורת המספרים הזו מציגה רק את \(0\) כל המספרים\(6\), המספרים ממשיכים בלי סוף.

ביצוע פעילות המתמטיקה המניפולטיבית "קו מספר 1" יעזור לך לפתח הבנה טובה יותר של מספרי הספירה והמספרים השלמים.

מערכת המספרים שלנו נקראת מערכת ערכי מקום, מכיוון שערך הספרה תלוי במיקומה במספר. איור \(\PageIndex{2}\) מציג את ערכי המקום. ערכי המקום מופרדים לקבוצות של שלוש, הנקראות תקופות. התקופות הן אלה, אלפים, מיליונים, מיליארדים, טריליונים וכן הלאה. במספר כתוב, פסיקים מפרידים בין התקופות.

איור\(\PageIndex{2}\): המספר \(5278194\) מוצג בתרשים. הספרה \(5\) נמצאת במקום המיליונים. הספרה \(2\) נמצאת במקום של מאה אלפים. הספרה \(7\) נמצאת במקום עשרת אלפים. הספרה \(8\) נמצאת במקום האלפים. הספרה \(1\) נמצאת במקום מאות. הספרה \(9\) נמצאת במקום העשרות. הספרה \(4\) נמצאת במקום אחד.

תרגיל \(\PageIndex{1}\)

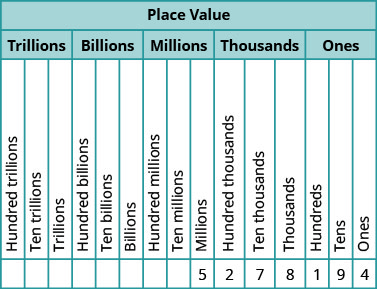
במספר\(63407218\), מצא את ערך המקום של כל ספרה:

1. \(7\)
2. \(0\)
3. \(1\)
4. \(6\)
5. \(3\)

תשובה

מקם את המספר בתרשים ערכי המקום:

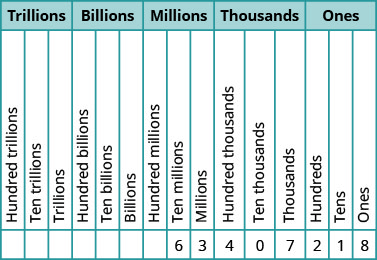
1. הוא \(7\) נמצא במקום של אלפים.
2. \(0\)הוא נמצא במקום עשרת אלפים.
3. הוא \(1\) נמצא במקום העשרות.
4. הוא \(6\) נמצא במקום של עשרה מיליון.
5. הוא \(3\) נמצא במקום המיליונים.

תרגיל \(\PageIndex{2}\)

עבור המספר\(27493615\), מצא את ערך המקום של כל ספרה:

1. 2
2. 1
3. 4
4. 7
5. 5

תשובה

1. עשרה מיליון
2. עשרות
3. מאות אלפים
4. מיליונים
5. אלה

תרגיל \(\PageIndex{3}\)

עבור המספר\(519711641328\), מצא את ערך המקום של כל ספרה:

1. 9
2. 4
3. 2
4. 6
5. 7

תשובה

1. מיליארדים
2. עשרת אלפים
3. עשרות
4. מאות אלפים
5. מאה מיליון

כשאתה כותב צ'ק אתה כותב את המספר במילים כמו גם בספרות. כדי לכתוב מספר במילים, כתוב את המספר בכל תקופה, ואחריו את שם התקופה, ללא ה - s בסוף. התחל בצד שמאל, שם לתקופות יש את הערך הגדול ביותר. תקופת אלה לא נקראת. הפסיקים מפרידים בין התקופות, כך שבכל מקום שיש פסיק במספר, שים פסיק בין המילים (ראה איור). \(\PageIndex{3}\) המספר \(74218369\) כתוב כשבעים וארבעה מיליון, מאתיים שמונה עשרה אלף, שלוש מאות שישים ותשע.

איור \(\PageIndex{3}\)

תן שם למספר שלם במילים.

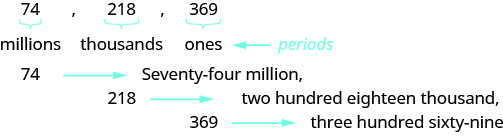
1. התחל משמאל ושם את המספר בכל תקופה, ואחריו שם התקופה.
2. שים פסיקים במספר כדי להפריד בין התקופות.
3. אל תציין את אלה תקופה.

תרגיל \(\PageIndex{4}\)

תן שם למספר \(8165432098710\) באמצעות מילים.

תשובה

תן שם למספר בכל תקופה, ואחריו שם התקופה.

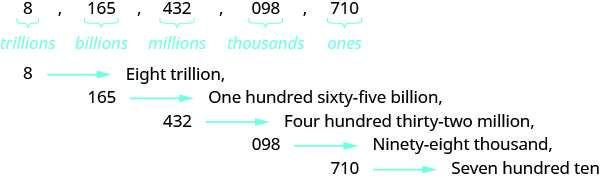
הכנס את הפסיקים כדי להפריד בין התקופות.

אז, \(8165432098710\) נקרא כשמונה טריליון, מאה שישים וחמישה מיליארד, ארבע מאות שלושים ושניים מיליון, תשעים ושמונה אלף, שבע מאות עשר.

תרגיל \(\PageIndex{5}\)

תן שם למספר 9,258,137,904,0619,258,137,904,061 באמצעות מילים.

תשובה

תשעה טריליון, מאתיים חמישים ושמונה מיליארד, מאה שלושים ושבעה מיליון, תשע מאות ארבעה אלף, שישים ואחד

תרגיל \(\PageIndex{6}\)

תן שם למספר 17,864,325,619,00417,864,325,619,004 באמצעות מילים.

תשובה

שבעה-עשר טריליון, שמונה מאות שישים וארבעה מיליארד, שלוש מאות עשרים וחמישה מיליון, שש מאות תשעה-עשר אלף ארבעה

כעת אנו הולכים להפוך את התהליך על ידי כתיבת הספרות משם המספר. כדי לכתוב את המספר בספרות, אנו מחפשים תחילה את מילות הרמז המציינות את התקופות. כדאי לצייר שלושה ריקים לתקופות הדרושות ואז למלא את החסר במספרים, ולהפריד בין התקופות לפסיקים.

כתוב מספר שלם באמצעות ספרות.

1. זהה את המילים המציינות תקופות. (זכור, תקופת אלה אף פעם לא נקראת.)
2. צייר שלושה ריקים כדי לציין את מספר המקומות הדרושים בכל תקופה. הפרד את התקופות בפסיקים.
3. תן שם למספר בכל תקופה והנח את הספרות במיקום ערך המקום הנכון.

תרגיל \(\PageIndex{7}\)

כתוב תשעה מיליארד, מאתיים ארבעים ושישה מיליון, שבעים ושלושה אלף, מאה שמונים ותשע כמספר שלם באמצעות ספרות.

תשובה

זהה את המילים המציינות תקופות.
למעט התקופה הראשונה, כל התקופות האחרות חייבות להיות בעלות שלושה מקומות. צייר שלושה ריקים כדי לציין את מספר המקומות הדרושים בכל תקופה. הפרד את התקופות בפסיקים.
לאחר מכן כתוב את הספרות בכל תקופה.

המספר הוא 9,246,073,189.

תרגיל \(\PageIndex{8}\)

כתוב את המספר שני מיליארד, ארבע מאות שישים ושישה מיליון, שבע מאות ארבע עשרה אלף, חמישים ואחת כמספר שלם באמצעות ספרות.

תשובה

2,466,714,051

תרגיל \(\PageIndex{9}\)

כתוב את המספר אחד עשר מיליארד, תשע מאות עשרים ואחד מיליון, שמונה מאות שלושים אלף, מאה שש כמספר שלם באמצעות ספרות.

תשובה

11,921,830,106

בשנת 2013 העריכה לשכת המפקד האמריקאית את אוכלוסיית מדינת ניו יורק כ -19,651,127. אפשר לומר שאוכלוסיית ניו יורק מנתה כ -20 מיליון. במקרים רבים אינך זקוק לערך המדויק; מספר משוער מספיק טוב.

תהליך קירוב מספר נקרא עיגול. מספרים מעוגלים לערך מקום מסוים, תלוי כמה דיוק נדרש. האמירה שאוכלוסיית ניו יורק מונה כ -20 מיליון פירושה שעגלנו למקום המיליונים.

תרגיל \(\PageIndex{10}\) How to Round Whole Numbers

סיבוב 23,658 למאה הקרובה ביותר.

תשובה

תרגיל \(\PageIndex{11}\)

סיבוב למאה הקרובה ביותר: 17,852.

תשובה

17,900

תרגיל \(\PageIndex{12}\)

סיבוב למאה הקרובה ביותר: 468,751.

תשובה

468,800

מספרים שלמים עגולים.

1. אתר את ערך המקום הנתון וסמן אותו בחץ. כל הספרות משמאל לחץ אינן משתנות.
2. הדגיש את הספרה מימין לערך המקום הנתון.
3. האם הספרה הזו גדולה או שווה ל -5?
   • כן - הוסף 11 לספרה בערך המקום הנתון.
   • לא — אל תשנה את הספרה בערך המקום הנתון.
4. החלף את כל הספרות מימין לערך המקום הנתון באפסים.

תרגיל \(\PageIndex{13}\)

סיבוב עגול 103,978103,978 אל הקרוב ביותר:

1. מאה
2. אלף
3. עשרת אלפים

תשובה

1.

אתר את המקום של מאות בשנת 103,978.
הדגיש את הספרה מימין למקום מאות.
מכיוון ש- 7 גדול או שווה ל- 5, הוסף 1 ל- 9. החלף את כל הספרות מימין למקום מאות באפסים.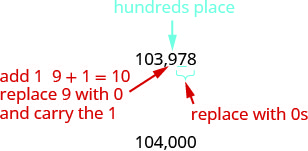
	אז, 104,000 הוא 103,978 מעוגל למאה הקרובה ביותר.

2.

אתר את מקום האלפים והדגיש את הספרה מימין למקום האלפים.
מכיוון ש- 9 גדול או שווה ל- 5, הוסף 1 ל- 3. החלף את כל הספרות מימין למקום מאות באפסים.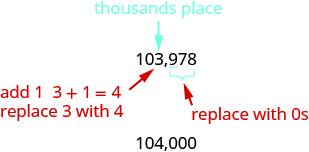
	אז, 104,000 הוא 103,978 מעוגל לאלף הקרוב ביותר.

3.

אתר את מקום עשרת אלפים והדגיש את הספרה מימין למקום עשרת אלפים.
מכיוון ש -3 הוא פחות מ -5, אנו משאירים את ה- 0 כפי שהוא ואז מחליפים את הספרות ימינה באפסים.
	אז 100,000 הוא 103,978 מעוגל לעשרת אלפים הקרובים ביותר.

תרגיל \(\PageIndex{14}\)

סיבוב 206,981 הקרוב ביותר: 1. מאה 2. אלף 3. עשרת אלפים.

תשובה

1. 207,000
2. 207,000
3. 210,000

תרגיל \(\PageIndex{15}\)

סיבוב 784,951 הקרוב ביותר: 1. מאה 2. אלף 3. עשרת אלפים.

תשובה

1. 785,000
2. 785,000
3. 780,000

זהה מכפילים והחל מבחני חלוקה

המספרים 2, 4, 6, 8, 10 ו -12 נקראים כפולות של 2. ניתן לכתוב מכפיל של 2 כתוצר של מספר ספירה ו -2.

איור \(\PageIndex{4}\)

באופן דומה, מכפיל של 3 יהיה תוצר של מספר ספירה ו -3.

איור \(\PageIndex{5}\)

נוכל למצוא את הכפולות של כל מספר על ידי המשך תהליך זה.

הערה

ביצוע פעילות המתמטיקה המניפולטיבית "מכפילים" יעזור לך לפתח הבנה טובה יותר של מכפילים.

הטבלה \(\PageIndex{1}\) מציגה את הכפולות של 2 עד 9 עבור 12 המספרים הראשונים.

טבלה \(\PageIndex{1}\)

ספירת מספר	1	2	3	4	5	6	7	8	9	10	11	12
מכפילים של 2	2	4	6	8	10	12	14	16	18	20	22	24
מכפילים של 3	3	6	9	12	15	18	21	24	27	30	33	36
מכפילים של 4	4	8	12	16	20	24	28	32	36	40	44	48
מכפילים של 5	5	10	15	20	25	30	35	40	45	50	55	60
כפולות של 6	6	12	18	24	30	36	42	48	54	60	66	72
מכפילים של 7	7	14	21	28	35	42	49	56	63	70	77	84
כפולות של 8	8	16	24	32	40	48	56	64	72	80	88	96
מכפילים של 9	9	18	27	36	45	54	63	72	81	90	99	108
מכפילים של 10	10	20	30	40	50	60	70	80	90	100	110	120

ריבוי של מספר

מספר הוא מכפיל של \(n\) אם הוא תוצר של מספר ספירה ו\(n\).

דרך נוספת לומר ש -15 הוא מכפיל של 3 היא לומר ש -15 מתחלק ב -3. זה אומר שכאשר אנו מחלקים 3 ל -15, אנו מקבלים מספר ספירה. למעשה, \(15\div 3\) הוא 5, אז 15 הוא\(5\cdot3\).

מתחלק במספר

אם מספר \(m\) הוא מכפיל של\(n\), אז \(m\) הוא מתחלק על ידי \(n\)

תסתכל על הכפולות של \(5\) בטבלה\(\PageIndex{1}\). כולם מסתיימים ב -5 או 0. מספרים עם הספרה האחרונה של 5 או 0 מתחלקים ב- 5. בחיפוש אחר דפוסים אחרים בטבלה \(\PageIndex{1}\) המציגים כפולות של המספרים 2 עד 9, אנו יכולים לגלות את מבחני החלוקה הבאים:

מבחני חלוקה

מספר מתחלק על ידי:

• 2 אם הספרה האחרונה היא 0, 2, 4, 6 או 8.
• 3 אם סכום הספרות מתחלק ב -3.
• 5 אם הספרה האחרונה היא 5 או 0.
• 6 אם הוא מתחלק גם ב -2 וגם ב -3.
• 10 אם זה מסתיים ב-0.

תרגיל \(\PageIndex{16}\)

האם 5625 מתחלק ב -2? על ידי 3? על ידי 5? על ידי 6? עד 10?

תשובה

\[\begin{array} {ll} {\text{Is 5625 divisible by 2?}} &{} \\ {\text{Does it end in 0, 2, 4, 6, or 8?}} &{\text{No.}} \\ {} &{\text{5625 is not divisible by 2.}} \end{array}\]

\[\begin{array} {ll} {\text{Is 5625 divisible by 3?}} &{} \\ {\text{What is the sum of the digits?}} &{5 + 6 + 2 + 5 = 18} \\ {\text{Is the sum divisible by 3?}} &{\text{Yes, 5625 is divisible by 3.}} \end{array}\]

\[\begin{array} {ll} {\text{Is 5625 divisible by 5 or 10?}} &{} \\ {\text{What is the last digit? It is 5.}} &{\text{5625 is divisible by 5 but not by 10.}} \end{array}\]

\[\begin{array} {ll} {\text{Is 5625 divisible by 6?}} &{} \\ {\text{Is it divisible by both 2 and 3?}} &{\text{No, 5625 is not divisible by 2, so 5625 is }} \\ {} &{\text{not divisible by 6.}}\end{array}\]

תרגיל \(\PageIndex{17}\)

קבע אם 4,962 מתחלק ב- 2, ב- 3, ב- 5, ב- 6 וב- 10.

תשובה

על ידי 2, 3 ו -6

תרגיל \(\PageIndex{18}\)

קבע אם 3,765 מתחלק ב- 2, ב- 3, ב- 5, ב- 6 וב- 10.

תשובה

על ידי 3 ו -5

מצא פקטוריזציות ראשוניות ומכפילים פחות נפוצים

במתמטיקה, יש לעתים קרובות כמה דרכים לדבר על אותם רעיונות. עד כה, ראינו שאם \(m\) הוא מכפיל של\(n\), אנו יכולים לומר כי \(m\) הוא מתחלק על ידי\(n\). לדוגמה, מכיוון ש 72 הוא מכפיל של 8, אנו אומרים ש 72 מתחלק ב- 8. מכיוון ש 72 הוא מכפיל של 9, אנו אומרים ש 72 מתחלק ב- 9. אנו יכולים לבטא זאת בדרך אחרת.

מאז\(8\cdot 9=72\), אנו אומרים כי 8 ו 9 הם גורמים של 72. כאשר אנו כותבים\(72=8\cdot 9\), אנו אומרים שיש לנו בחשבון 72.

איור \(\PageIndex{6}\)

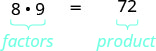
דרכים אחרות לגורם 72 הן\(1\cdot 72\),\(2\cdot 36\),\(3\cdot 24\), \(4\cdot 18\) ו\(6\cdot 12\). לשבעים ושניים גורמים רבים: 1, 2, 3, 4, 6, 8, 9, 12, 18, 36 ו -72.

גורמים

אם\(a\cdot b=m\), אז \(a\) \(b\) והם גורמים של\(m\).

למספרים מסוימים, כמו 72, יש גורמים רבים. למספרים אחרים יש רק שני גורמים.

הערה

ביצוע פעילות המתמטיקה המניפולטיבית "כפל מודל ופקטורינג" יעזור לך לפתח הבנה טובה יותר של כפל ופקטורינג.

מספר ראשוני ומספר ללא הפרדות צבע

מספר ראשוני הוא מספר ספירה הגדול מ -1, שהגורמים היחידים שלו הם 1 ועצמו.

מספר מורכב הוא מספר ספירה שאינו ראשוני. למספר מורכב יש גורמים שאינם 1 ועצמו.

הערה

ביצוע פעילות המתמטיקה המניפולטיבית "מספרים ראשוניים" יעזור לך לפתח הבנה טובה יותר של מספרים ראשוניים.

מספרי הספירה מ -2 עד 19 מפורטים באיור\(\PageIndex{7}\), עם הגורמים שלהם. הקפד להסכים עם התווית "פריים" או "מרוכב" עבור כל אחד!

איור \(\PageIndex{7}\)

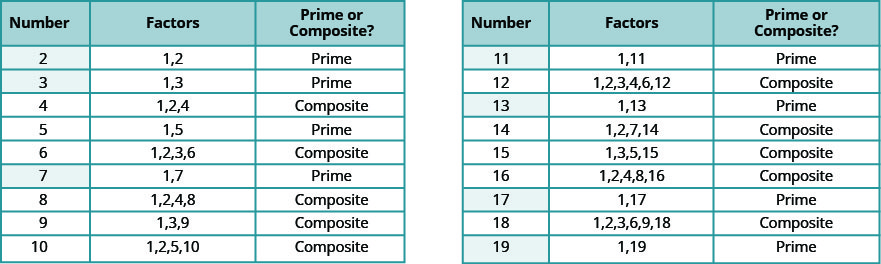
המספרים הראשוניים של פחות מ -20 הם 2, 3, 5, 7, 11, 13, 17 ו -19. שימו לב שהמספר הראשוני היחיד הוא 2.

ניתן לכתוב מספר מורכב כתוצר ייחודי של מספרים ראשוניים. זה נקרא פקטוריזציה ראשונית של המספר. מציאת הפקטוריזציה הראשונית של מספר מורכב תהיה שימושית בהמשך קורס זה.

פקטוריזציה ראשונית

הפקטוריזציה הראשונית של מספר היא תוצר של מספרים ראשוניים השווה למספר.

כדי למצוא את הפקטוריזציה הראשונית של מספר מורכב, מצא שני גורמים של המספר והשתמש בהם ליצירת שני סניפים. אם גורם הוא ראשוני, הענף הזה הושלם. הקף את הפריים הזה!

אם הגורם אינו ראשוני, מצא שני גורמים למספר והמשיך בתהליך. לאחר שכל הענפים הקיפו את המספרים הראשוניים בסוף, הפקטוריזציה הושלמה. כעת ניתן לכתוב את המספר המורכב כתוצר של מספרים ראשוניים.

תרגיל \(\PageIndex{19}\)

פקטור 48.

תשובה

אנו אומרים \(2\cdot 2\cdot 2\cdot 2\cdot 3\) שהוא הפקטוריזציה העיקרית של 48. בדרך כלל אנו כותבים את המספרים הראשוניים בסדר עולה. הקפד להכפיל את הגורמים כדי לאמת את תשובתך!

אם היינו לוקחים בחשבון 48 בצורה אחרת, למשל\(6\cdot 8\), התוצאה עדיין תהיה זהה. סיים את הפקטוריזציה הראשונית וודא זאת בעצמך.

תרגיל \(\PageIndex{20}\)

מצא את הפקטוריזציה העיקרית של 80.

תשובה

\(2\cdot 2\cdot 2\cdot 2\cdot 5\)

תרגיל \(\PageIndex{21}\)

מצא את הפקטוריזציה העיקרית של 60.

תשובה

\(2\cdot 2\cdot 3\cdot 5\)

מצא את הפקטוריזציה הראשונית של מספר מורכב.

1. מצא שני גורמים שהמוצר שלהם הוא המספר הנתון, והשתמש במספרים אלה כדי ליצור שני סניפים.
2. אם גורם הוא ראשוני, הענף הזה הושלם. הקף את הפריים, כמו ניצן על העץ.
3. אם גורם אינו ראשוני, כתוב אותו כתוצר של שני גורמים והמשיך בתהליך.
4. כתוב את המספר המורכב כתוצר של כל המספרים הראשוניים המוקפים.

תרגיל \(\PageIndex{22}\)

מצא את הפקטוריזציה העיקרית של 252.

תשובה

שלב 1. מצא שני גורמים שהמוצר שלהם הוא 252. 12 ו -21 אינם ראשוניים. לשבור 12 ו 21 לשני גורמים נוספים. המשך עד שכל המספרים הראשוניים ייחשבו.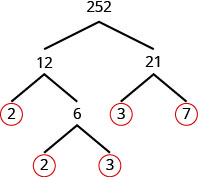
שלב 2. כתוב 252 כתוצר של כל המספרים הראשוניים המוקפים.	\(252=2\cdot 2\cdot 3\cdot 3\cdot 7\)

תרגיל \(\PageIndex{23}\)

מצא את הפקטוריזציה העיקרית של 126.

תשובה

\(2\cdot 3\cdot 3\cdot 7\)

תרגיל \(\PageIndex{24}\)

מצא את הפקטוריזציה העיקרית של 294.

תשובה

\(2\cdot 3\cdot 7\cdot 7\)

אחת הסיבות שאנו מסתכלים על כפולות וראשוניות היא להשתמש בטכניקות אלה כדי למצוא את הכפולה הפחות נפוצה של שני מספרים. זה יהיה שימושי כאשר נוסיף ונחסך שברים עם מכנה שונים.שתי שיטות משמשות לרוב למציאת הכפולה הפחות נפוצה ונבחן את שתיהן.

השיטה הראשונה היא שיטת ריבוי הרישום. כדי למצוא את הכפולה הפחות נפוצה של 12 ו -18, אנו מפרטים את הכפולות הראשונות של 12 ו -18:

איור \(\PageIndex{8}\)

שימו לב שמספרים מסוימים מופיעים בשתי הרשימות. הם הכפולות הנפוצות של 12 ו -18.

אנו רואים שהכפולות הנפוצות הראשונות של 12 ו -18 הן 36, 72 ו -108. מכיוון ש- 36 הוא הקטן מבין הכפולות הנפוצות, אנו מכנים אותו הכפולה הפחות נפוצה. לעתים קרובות אנו משתמשים בקיצור LCM.

מכפיל פחות נפוץ

הכפולה הפחות נפוצה (LCM) של שני מספרים היא המספר הקטן ביותר שהוא מכפיל של שני המספרים.

תיבת ההליך מפרטת את הצעדים שיש לנקוט כדי למצוא את ה- LCM בשיטת הגורמים הראשוניים בהם השתמשנו לעיל עבור 12 ו -18.

מצא את הכפולה הפחות נפוצה על ידי רישום מכפילים.

1. רשום מספר מכפילים של כל מספר.
2. חפש את המספר הקטן ביותר שמופיע בשתי הרשימות.
3. מספר זה הוא LCM.

תרגיל \(\PageIndex{25}\)

מצא את הכפולה הפחות נפוצה של 15 ו -20 על ידי רישום מכפילים.

תשובה

ערכו רשימות של הכפולות הראשונות של 15 ושל 20, והשתמשו בהן כדי למצוא את הכפולה הפחות נפוצה.
חפש את המספר הקטן ביותר שמופיע בשתי הרשימות.	המספר הראשון שמופיע בשתי הרשימות הוא 60, ולכן 60 הוא הכפולה הפחות נפוצה של 15 ו -20.

שימו לב שגם 120 נמצא בשתי הרשימות. זהו מכפיל נפוץ, אך הוא אינו המכפיל הפחות נפוץ.

תרגיל \(\PageIndex{26}\)

מצא את הכפולה הפחות נפוצה על ידי רישום מכפילים: 9 ו-12.

תשובה

\(36\)

תרגיל \(\PageIndex{27}\)

מצא את הכפולה הפחות נפוצה על ידי רישום מכפילים: 18 ו -24.

תשובה

\(72\)

השיטה השנייה שלנו למצוא את הכפולה הפחות נפוצה של שני מספרים היא להשתמש בשיטת הגורמים הראשוניים. בואו למצוא את LCM של 12 ו 18 שוב, הפעם באמצעות הגורמים העיקריים שלהם.

תרגיל \(\PageIndex{28}\)

מצא את הכפולה הפחות נפוצה (LCM) של 12 ו -18 בשיטת הגורמים הראשוניים.

תשובה

שימו לב שהגורמים העיקריים של \(12(2\cdot 2\cdot 3)\) והגורמים העיקריים של \(18(2\cdot 3\cdot 3)\) כלולים ב- LCM\((2\cdot 2\cdot 3\cdot 3)\). אז 36 הוא הכפולה הפחות נפוצה של 12 ו -18.

על ידי התאמת המספרים הראשוניים הנפוצים, משתמשים בכל גורם ראשוני משותף פעם אחת בלבד. בדרך זו אתה בטוח ש- 36 הוא הכפולה הפחות נפוצה.

תרגיל \(\PageIndex{29}\)

מצא את ה- LCM בשיטת הגורמים הראשוניים: 9 ו -12.

תשובה

\(36\)

תרגיל \(\PageIndex{30}\)

מצא את ה- LCM בשיטת הגורמים הראשוניים: 18 ו -24.

תשובה

\(72\)

מצא את הכפולה הפחות נפוצה בשיטת PRIME FACTORS.

1. כתוב כל מספר כתוצר של מספרים ראשוניים.
2. רשום את המספרים הראשוניים של כל מספר. התאם את המספרים הראשוניים אנכית במידת האפשר.
3. תוריד את העמודות.
4. הכפל את הגורמים.

תרגיל \(\PageIndex{31}\)

מצא את הכפולה הפחות נפוצה (LCM) של 24 ו -36 בשיטת הגורמים הראשוניים.

תשובה

מצא את המספרים הראשוניים של 24 ו -36. התאם את המספרים הראשוניים אנכית במידת האפשר. להפיל את כל העמודות.
הכפל את הגורמים.
	ה- LCM של 24 ו -36 הוא 72.

תרגיל \(\PageIndex{32}\)

מצא את ה- LCM בשיטת הגורמים הראשוניים: 21 ו -28.

תשובה

\(84\)

תרגיל \(\PageIndex{33}\)

מצא את ה- LCM בשיטת הגורמים הראשוניים: 24 ו- 32.

תשובה

\(96\)

הערה

גש למשאב מקוון זה לקבלת הדרכה ותרגול נוספים באמצעות מספרים שלמים. יהיה עליך להפעיל את Java בדפדפן האינטרנט שלך כדי להשתמש ביישום.

• מסננת של ארטוסטנס

מושגי מפתח

• ערך מקום כמו באיור.
• שם מספר שלם במילים
  1. התחל משמאל ושם את המספר בכל תקופה, ואחריו שם התקופה.
  2. שים פסיקים במספר כדי להפריד בין התקופות.
  3. אל תציין את אלה תקופה.
• כתוב מספר שלם באמצעות ספרות
  1. זהה את המילים המציינות תקופות. (זכור שתקופת אלה אף פעם לא נקראת.)
  2. צייר 3 ריקים כדי לציין את מספר המקומות הדרושים בכל תקופה. הפרד את התקופות בפסיקים.
  3. תן שם למספר בכל תקופה והנח את הספרות במיקום ערך המקום הנכון.
• מספרים שלמים עגולים
  1. אתר את ערך המקום הנתון וסמן אותו בחץ. כל הספרות משמאל לחץ אינן משתנות.
  2. הדגיש את הספרה מימין לערך המקום הנתון.
  3. האם הספרה הזו גדולה או שווה ל -5?
     • כן - הוסף 1 לספרה בערך המקום הנתון.
     • לא — אל תשנה את הספרה בערך המקום הנתון.
  4. החלף את כל הספרות מימין לערך המקום הנתון באפסים.
• מבחני חלוקה: מספר מתחלק ב:
  • 2 אם הספרה האחרונה היא 0, 2, 4, 6 או 8.
  • 3 אם סכום הספרות מתחלק ב -3.
  • 5 אם הספרה האחרונה היא 5 או 0.
  • 6 אם הוא מתחלק גם ב -2 וגם ב -3.
  • 10 אם זה מסתיים ב-0.
• מצא את הפקטוריזציה הראשונית של מספר מורכב
  1. מצא שני גורמים שהמוצר שלהם הוא המספר הנתון, והשתמש במספרים אלה כדי ליצור שני סניפים.
  2. אם גורם הוא ראשוני, הענף הזה הושלם. הקף את הפריים, כמו ניצן על העץ.
  3. אם גורם אינו ראשוני, כתוב אותו כתוצר של שני גורמים והמשיך בתהליך.
  4. כתוב את המספר המורכב כתוצר של כל המספרים הראשוניים המוקפים.
• מצא את הכפולה הפחות נפוצה על ידי רישום מכפילים
  1. רשום מספר מכפילים של כל מספר.
  2. חפש את המספר הקטן ביותר שמופיע בשתי הרשימות.
  3. מספר זה הוא LCM.
• מצא את הכפולה הפחות נפוצה בשיטת גורמים ראשוניים
  1. כתוב כל מספר כתוצר של מספרים ראשוניים.
  2. רשום את המספרים הראשוניים של כל מספר. התאם את המספרים הראשוניים אנכית במידת האפשר.
  3. תוריד את העמודות.
  4. הכפל את הגורמים.

רשימת מילים

מספר מרוכב

מספר מורכב הוא מספר ספירה שאינו ראשוני. למספר מורכב יש גורמים שאינם 1 ועצמו.

ספירת מספרים

מספרי הספירה הם המספרים 1, 2, 3,...

מתחלק במספר

אם מספר \(m\) הוא כפולה של\(n\), אז \(m\) הוא מתחלק על ידי\(n\). (אם 6 הוא מכפיל של 3, אז 6 מתחלק ב -3.)

גורמים

אם\(a\cdot b=m\), אז \(a\) \(b\) והם גורמים של\(m\). מאז\(3 \cdot 4 = 12\), אז 3 ו -4 הם גורמים של 12.

המרובה הפחות נפוצה

הכפולה הפחות נפוצה של שני מספרים היא המספר הקטן ביותר שהוא מכפיל של שני המספרים.

מכפיל של מספר

מספר הוא מכפיל של \(n\) אם הוא תוצר של מספר ספירה ו\(n\).

שורת מספר

שורת מספרים משמשת להמחשת מספרים. המספרים בשורת המספרים גדלים ככל שהם עוברים משמאל לימין, וקטנים ככל שהם עוברים מימין לשמאל.

מוצא

המקור הוא הנקודה שכותרתה 0 בשורת מספרים.

פקטוריזציה ראשונית

הפקטוריזציה הראשונית של מספר היא תוצר של מספרים ראשוניים השווה למספר.

מספר ראשוני

מספר ראשוני הוא מספר ספירה הגדול מ -1, שהגורמים היחידים שלו הם 1 ועצמו.

מספרים שלמים

המספרים השלמים הם המספרים 0, 1, 2, 3,...