7.5: أشكال معادلة الخط المستقيم
- Page ID
- 166943
شرح القسم السابق معادلات الخطوط الرأسية والأفقية. اكتشف الآن ثلاثة أشكال أخرى لمعادلات الخط، وهي نموذج المنحدر المقطوع، ونموذج النقطة المنحدرة، والنموذج القياسي.
صورة المنحدر والجزء المقطوع من معادلة الخط المستقيم
شكل المنحدر المقطوع لمعادلة الخط المستقيم هو بالشكل التالي:
\[y = mx + b \nonumber \]
\(m\)أين منحدر الخط الفاصل\((0, b)\) وهو الجزء\(y\) المقطوع.
لاحظ أن\(y\) التقاطع -هو النقطة التي يتقاطع فيها الخط مع\(y\) المحور −، أي عندما\(x = 0\).
اكتب معادلة الخط المستقيم الذي يحتوي على المنحدرات\(y\) المعطاة ونقاط التقاطع.
- المنحدر =\(5\)؛\(y\) −التقاطع\((0, \dfrac{1}{2})\)
- المنحدر =\(−\dfrac{5}{6}\)؛\(y\) - الاعتراض\((0, −\dfrac{3}{4})\)
الحل
- \(m = 5\)و\(b = \dfrac{1}{2}\)
معادلة الخط المستقيم هي الرابعة\(y = mx + b\). وهكذا،
\(\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &= 5x + \dfrac{1}{2} &\text{Substitute \(m = 5\)و\(b = \dfrac{1}{2}\)}\ end {المصفوفة}\)
لذلك،\(y = 5x + \dfrac{1}{2}\) هي معادلة الخط المستقيم الذي يحتوي على المنحدر المُعطى\(y\) والجزء المقطوع.
- نظرا\(m = −\dfrac{5}{6}\) و\(b = −\dfrac{3}{4}\)
وهكذا،
\(\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &= −\dfrac{5}{6}x −\dfrac{3}{4} &\text{Substitute values} \end{array}\)
لذلك،\(y = −\dfrac{5}{6}x − \dfrac{3}{4}\) هي معادلة الخط المستقيم الذي يحتوي على المنحدر المُعطى\(y\) والجزء المقطوع.
حدِّد المنحدر ثم الجزء\(y\) المقطوع، ثم استخدمهما لتمثيل كل خط بيانيًّا.
- \(y = −2x + 4\)
- \(5y − 3x = 10\)
الحل
أ- لاحظ أن المعادلة الخطية المعطاة هي في صورة التقاطع المنحدر. لذلك،\(m = −2\) أو بما يعادل ذلك،\(m = −\dfrac{2}{1}\) و\(b = 4\)
\(m\)هو منحدر الخط، إذن\(m = \dfrac{\text{rise}}{\text{run}} = −\dfrac{2}{1}\). لرسم الخط، ارسم نقطتين على الأقل. ابدأ عند\(y\) التقاطع −\((0, 4)\) ثم انتقل إلى\(2\) الوحدة السفلية ثم انتقل إلى\(1\) الوحدة اليمنى لرسم النقطة الثانية. الآن قم بربط النقطتين بخط مستقيم كما هو موضح في الشكل أدناه.
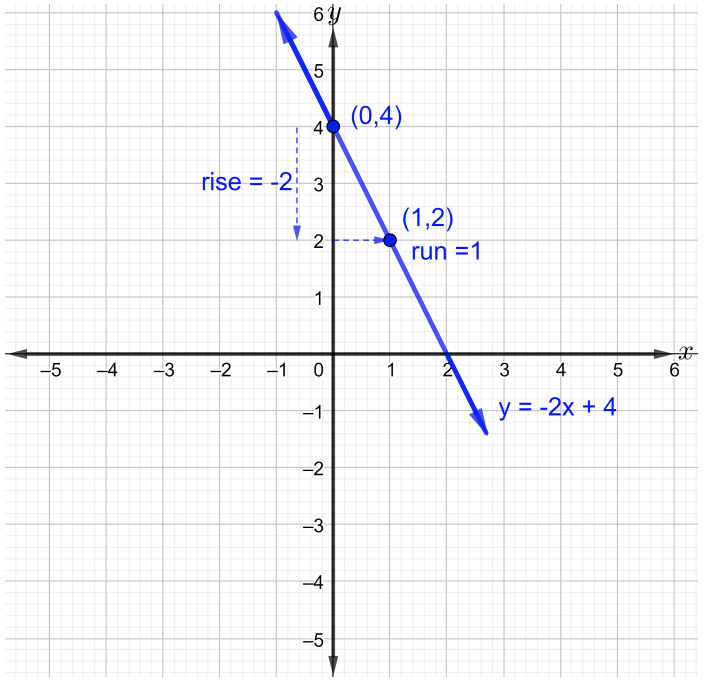
ب- لاحظ أنه ليس من الواضح كيفية تحديد المنحدر والجزء\(y\) المقطوع في هذه المعادلة الخطية المعطاة لأنها ليست في شكل المنحدر والفاصل. وهكذا، قم\(y\) بحل المعادلة في الصورة المقطوعة للانحدار كما يلي،
\(\begin{array} &&5y − 3x = −10 &\text{Given} \\ &5y = 3x − 10 &\text{Add \(3x\)على جانبي المعادلة}\\ &y =\ dfrac {3} {5} x − 2 &\ text {قسّم كل المصطلحات\(5\) إلى العزل\(y\)}\ end {المصفوفة}\)
الآن،\(m = \dfrac{3}{5}\) و\(b = −2\). ابدأ برسم\(y\) التقاطع\((0, −2)\) -ثم انقل\(3\) الوحدات لأعلى\(5\) والوحدات إلى اليمين وارسم النقطة الثانية وهي\((5, 1)\). الآن، قم بربط النقطتين،\((0, −2)\) أي\((5, 1)\) للحصول على الرسم البياني للخط الموضح في الشكل أدناه.
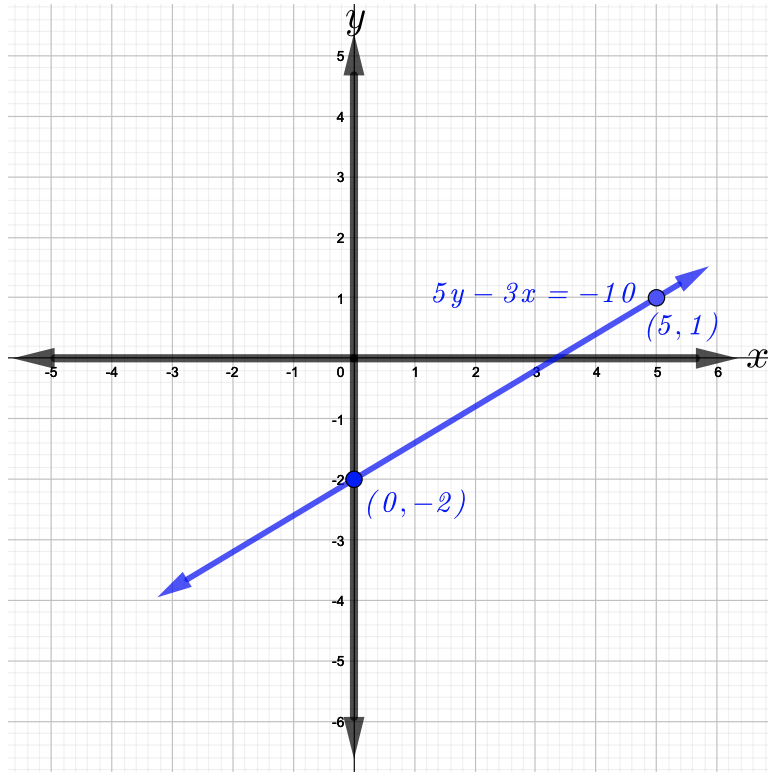
اكتب معادلة الخط المستقيم الذي يحتوي على المنحدر المُعطى والجزء\(y\) المقطوع من نقطة التقاطع.
- المنحدر:\(2\)\(y\) -التقاطع:\((0, \dfrac{3}{4})\)
- المنحدر:\(\dfrac{5}{7}\)\(y\) -التقاطع:\((0, −6)\)
- المنحدر:\(−\dfrac{1}{2}\)\(y\) -التقاطع:\((0, −\dfrac{7}{11} )\)
حدد المنحدر والجزء\(y\) المقطوع ثم استخدمهما لرسم كل خط بيانيًا.
- \(y = 5x − 3\)
- \(2y = −6x + 1\)
صيغة النقطة المنحدرة لمعادلة الخط المستقيم
نموذج نقطة المنحدر لمعادلة الخط المستقيم هو:
\[y − y_1 = m(x − x_1) \nonumber \]
\(m\)أين منحدر الخط وأي\((x_1, y_1)\) نقطة على الخط المستقيم.
أوجد معادلة كل خط يمر بالنقطة المُعطاة ومنحدرًا مُعطى.
- المنحدر\(3\) والنقطة\((−1, 8)\)
- المنحدر\(−\dfrac{5}{2}\) والنقطة\((\dfrac{4}{3}, \dfrac{1}{3})\)
الحل
- للعثور على معادلة الخط الذي يمر بالنقطة\((−1, 8)\) ذات المنحدر\(m = 3\)، استخدم نموذج نقطة المنحدر كما يلي:
\(\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ &y − 8 = 3[x − (−1)] &\text{Substitute \(m = 3\)\(x_1 = −1\), و\(y_1 = 8\)}\\ &y − 8 = 3 (x + 1) و\ text {تبسيط}\\\ &y − 8 = 3x + 3 &\ text {اضرب كلا المصطلحين على يمين المعادلة بـ\(3\)}\\\ &y = 3x + 11 &\ text {أضف\(8\) إلى جانبي المساواة لعزل\(y\)}\ نهاية {المصفوفة}\)
لذلك،\(y = 3x + 11\) هي معادلة الخط المستقيم الذي يحتوي على المنحدر والنقطة المُعطاة. الخط في شكل التقاطع المنحدر.
- على غرار الجزء أ، استخدم نموذج Point-Slope كما يلي:
\(\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ & y−(−\dfrac{1}{3}) = −\dfrac{5}{2} (x −\dfrac{4}{3}) &\text{Substitute \(m = −\dfrac{5}{2},\;\; x_1 = \dfrac{4}{3}\), و\(y_1 = −\dfrac{1}{3}\)}\\ &y +\ dfrac {1} {3} = −\ dfrac {5} {2} x +\ dfrac {20} {6} و\ النص {التوزيع والتبسيط}\\\ y = −\ dfrac {5} {2} x +\ dfrac {6} −\ dfrac {1} {3} & النص {2}\(\dfrac{1}{3}\) من كلا الجانبين}\\ &y = −\ dfrac {5} {2} x + 3 &\ text {لدمج الجزأين، لاحظ ما يلي: شاشة LCD\(= 6\).}\\ &\ text {اضرب البسط والمقام لـ\(\dfrac{1}{3}\) y\(2\) وقم بتبسيط:}\\ & &\ text {\(\dfrac{20}{6} − \dfrac{1(2)}{3(2)} = \dfrac{20}{6} − \dfrac{2}{6} = \dfrac{18}{6} = 3\)}\ end {المصفوفة}\)
لذلك،\(y = −\dfrac{5}{2}x + 3\) هي معادلة الخط المستقيم الذي يمر بنقطة العطاء والمنحدر المعطى.
ابحث عن معادلة الخط المعطى بالنقاط\((2, 4)\) و\((−3, 9)\).
لاحظ أنه في وقت سابق من هذا الفصل شرح كيفية إيجاد معادلة الخط المستقيم بمعلومية المنحدر\(y\) والجزء المقطوع. يشرح هذا الفصل أيضًا كيفية إيجاد معادلة الخط المستقيم بمعلومية أي نقطة على الخط والمنحدر. لذلك، في كلتا الطريقتين، يتم إعطاء المنحدر.
الحل
لإيجاد معادلة خط مستقيم بمعلومية أي نقطتين على الخط المستقيم، أوجد أولًا الميل باستخدام ميل صيغة الخط المستقيم. بعد ذلك، قم بتطبيق نموذج نقطة المنحدر مع أي من النقاط المحددة. أولاً، استخدم النقطتين للعثور على ميل الخط. دعونا\((x_1, y_1) = (2, 4)\) و\((x_2, y_2) = (−3, 9)\). ثم،
\(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{Slope of the line formula} \\ &= \dfrac{9 − 4}{−3 − 2} &\text{Substitute values} \\ &= \dfrac{5}{−5} &\text{Simplify} \\ &= −1 & \end{array}\)
الآن تم العثور على المنحدر، لذا ابحث بعد ذلك عن معادلة الخط باستخدام أي من النقاط المعطاة. وبالتالي،\(m = −1\) فكر في استخدام النقطة\((2, 4)\).
\(\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-slope form} \\ &y − 4 = −1(x − 2) &\text{Substitute \(m = −1\)\(x_1 = 2\),\(y_1 = 4\)}\\ &y − 4 = −x + 2 &\ text {قم\(-1\) بالتوزيع على كلا المصطلحين على اليمين}\\\ &y = −x + 6 &\ text {أضف\(4\) إلى جانبي المعادلة لعزل\(y\)}\ end {المصفوفة}\)
لذلك،\(y = −x + 6\) هي معادلة الخط الذي يمر عبر النقطة المعطاة ولها شكل المنحدر المقطوع.
أوجد معادلة كل خط يمر بالنقطة المُعطاة وله ميل مُعطى.
- المنحدر\(−\dfrac{5}{2}\) والنقطة\((3, 0)\).
- المنحدر\(\dfrac{1}{2}\) والنقطة\((−2, −3)\).
ابحث عن معادلة الخط بمعلومية النقاط التالية.
- \((−9, −3)\)و\((6, −2)\)
- \((4, 1)\)و\((−2, 2)\)
الشكل القياسي لمعادلة الخط المستقيم (المعروف أيضًا باسم الشكل العام للمعادلة الخطية)
الشكل القياسي للخط غير العمودي هو في النموذج
\[Ax + By = C \nonumber \]
أين\(A\) يوجد عدد صحيح موجب،\(B\)\(C\) والأعداد الصحيحة مع\(B \neq 0\).
رسم بياني لكل سطر من المعادلات التالية:
- \(4x − 3y = 6\)
- \(\dfrac{1}{2} − y + 1 = 0\)
لاحظ أن\(x\) التقاطع - هو النقطة التي يتقاطع فيها الخط مع\(x\) المحور -. هذا هو الوقت\(y = 0\). وبالتالي، فإن\(x\) -Intercept هي نقطة من النموذج\((a, 0)\)، حيث\(a\) يوجد أي رقم حقيقي.
الحل
- المعادلة\(4x − 3y = 6\) في الشكل القياسي. لرسم خط المعادلة المعطاة، قد يكون من الممكن استخدام أكثر من طريقة. على سبيل المثال، حل المشكلة\(y\) للحصول على المعادلة في صورة التقاطع المنحدر، ثم رسم الخط بيانيًا. من الممكن أيضًا العثور على نقطتين، ثم رسم الخط. أسهل نقطتين يمكن العثور عليهما بسرعة هما النقطة\(x\)\(y\) والاعتراض. لذلك، يوصى بهذه الطريقة.
لإيجاد\(x\) التقاطع السيني، ضع\(y = 0\) المعادلة المعطاة وحلّها\(x\) كما يلي:
\(\begin{array} &&4x − 3y = 6 &\text{Given} \\ &4x − 3(0) = 6 &\text{Substitute \(y = 0\)}\\ &4x = 6 &\ text {تبسيط}\\ &x =\ dfrac {6} {4}\\ text {القسمة على\(4\) جانبي المعادلة}\\\ &x =\ dfrac {3} {2}\\ النص {تبسيط}\ نهاية {مصفوفة}\)
وبالتالي، فإن\(x\) نقطة التقاطع هي النقطة\((\dfrac{3}{2}, 0)\)
الآن، للعثور على\(y\) التقاطع، اضبط على\(x = 0\) النحو التالي،
\(\begin{array} &&4x − 3y = 6 &\text{Given} \\ &4(0) − 3y = 6 &\text{Substitute \(x = 0\)}\\ &−3y = 6 &\ text {تبسيط}\\ &y = 6 −3 &\ النص {القسمة على\(−3\) جانبي المعادلة}\\\ &y = −2\ النص {تبسيط}\ نهاية {المصفوفة}\)
الآن، ارسم النقاط\((\dfrac{3}{2}, 0)\)\((0, −2)\) ورسم الخط المستقيم الذي يمر عبرها كما هو موضح في الشكل أدناه.
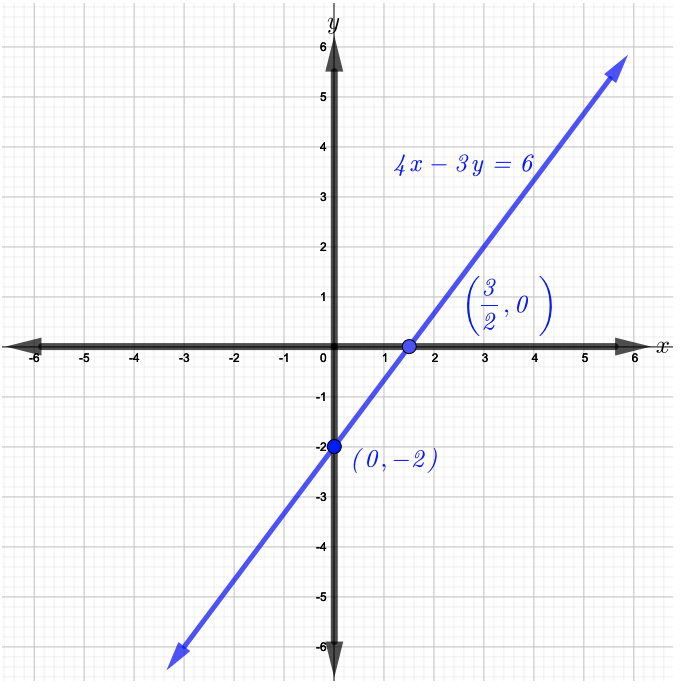
المعادلة\(\dfrac{1}{2} x − y + 1 = 0\) ليست في الشكل القياسي. لذلك، اطرح\(1\) من كلا طرفي المعادلة للحصول على\(\dfrac{1}{2}x − y = −1\) ما هو الآن في الصورة القياسية.
مرة أخرى، على غرار الجزء ب، ابحث عن\(x\) المعترضين و\(y\) -المعترضين. أولاً، ابحث عن\(x\) -incircept عن طريق الإعداد\(y = 0\) والحل على\(x\) النحو التالي.
\( \begin{array} &&\dfrac{1}{2}x − y = −1 &\text{Standard form of the given equation} \\ &\dfrac{1}{2}x − (0) = −1 &\text{Substitute \(y = 0\)}\\\ dfrac {1} {2} x = −1 &\ text {تبسيط}\\ &x = −2\\ text {اضرب\(2\) بكلا طرفي المعادلة.} \ end {مصفوفة}\)
وبالتالي، فإن النقطة\(x\) -Intercept هي النقطة\((−2, 0)\).
الآن، قم\(x = 0\) بتعيين البحث\(y\) عن التقاطع، كما يلي،
\( \begin{array} &&\dfrac{1}{2}x − y = −1 &\text{Standard form of the given equation} \\ &\dfrac{1}{2}(0) − y = −1 &\text{Substitute \(x = 0\)}\\ &−y = −1 &\ text {تبسيط}\\ &y = 1 &\ text {\(-1\)اضرب في} \ end {مصفوفة}\)
ومن ثم، فإن\(y\) نقطة التقاطع هي\((0, 1)\).
ارسم نقاط التقاطع\(x\)\(y\) و - ثم\((−2, 0)\) ارسم\((0, 1)\) الخط المستقيم الذي يمر عبرهما كما هو موضح في الشكل أدناه.
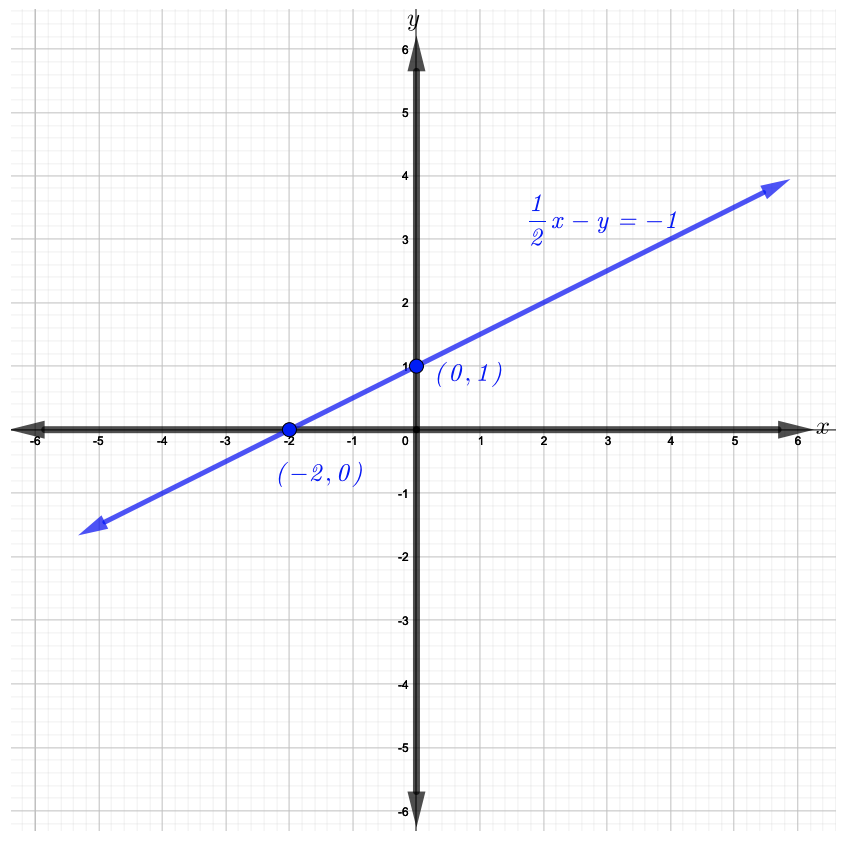
لا توجد واجبات منزلية لهذا القسم.


