8.1: Többszörös regresszió

Gyakran előfordul, hogy egy függő változó (y), amelyben érdekel, egynél több független változóhoz kapcsolódik. Ha ez az összefüggés megbecsülhető, akkor lehetővé teheti számunkra, hogy pontosabb előrejelzéseket készítsünk a függő változóról, mint egy egyszerű lineáris regresszióval lehetséges. Az egynél több független változón alapuló regressziókat többszörös regressziónak nevezzük.

A többszörös lineáris regresszió az egyszerű lineáris regresszió kiterjesztése, és sok ötlet, amelyet egyszerű lineáris regresszióban vizsgáltunk, átkerül a többszörös regressziós beállításra. Például a szórásdiagramok, a korreláció és a legkisebb négyzetek módszere továbbra is elengedhetetlen összetevői a többszörös regressziónak.

Például a fodros fajd élőhely-alkalmassági indexe (amelyet a vadon élő állatok élőhelyére gyakorolt földhasználati változások hatásának értékelésére használnak) három tényezőhöz kapcsolódhat:

x ₁ = szár sűrűsége
x ₂ = a tűlevelűek százaléka
x ₃ = az aljnövényzet lágyszárú anyag mennyisége

Egy kutató adatokat gyűjt ezekről a változókról, és a mintaadatok felhasználásával regressziós egyenletet állít össze, amely ezt a három változót a válaszhoz kapcsolja. A kutatónak kérdései lesznek a modelljével kapcsolatban, hasonlóan egy egyszerű lineáris regressziós modellhez.

• Mennyire erős a kapcsolat y és a három előrejelző változó között?
• Mennyire illeszkedik a modell?
• Megsértették-e valamilyen fontos feltételezést?
• Mennyire jók a becslések és előrejelzések?

Az általános lineáris regressziós modell formája

\[y_i = \beta_0+ \beta_1x_1+\beta_2x_2 + ...+\beta_kx_k+\epsilon\]

y középértékével megadva

\[\mu_y = \beta_0 +\beta_1 x_1+\beta_2 x_2+...+\beta_k x_k\]

ahol:

• y a véletlen válasz változó és μy az y átlagértéke,
• β0, β1, β2 és βk a mintaadatok alapján becsülendő paraméterek,
• x 1, x 2,..., x k azok a prediktor változók, amelyekről feltételezik, hogy nem véletlenszerűek vagy fixek, és hiba nélkül mérik, és k a prediktor változó száma,
• és ε a véletlenszerű hiba, amely lehetővé teszi, hogy minden válasz eltérjen az y átlagértékétől. Feltételezzük, hogy a hibák függetlenek, átlaguk nulla és közös szórásuk van (σ2), és normálisan eloszlanak.

Mint látható, a többszörös regressziós modell és feltételezések nagyon hasonlítanak egy egyszerű lineáris regressziós modellhez, egy prediktor változóval. A maradék parcellák és a maradékok normál valószínűségi diagramjainak vizsgálata kulcsfontosságú a feltételezések ellenőrzéséhez.

Korreláció

Az egyszerű lineáris regresszióhoz hasonlóan mindig a válaszváltozó szórásdiagramjával kell kezdenünk az egyes prediktor változókkal szemben. Az egyes párok lineáris korrelációs együtthatóit is ki kell számítani. Ahelyett, hogy az egyes párok korrelációját külön-külön számítanánk ki, létrehozhatunk egy korrelációs mátrixot, amely megmutatja a lineáris korrelációt az egyes vizsgált változópárok között egy többszörös lineáris regressziós modellben.

\(\begin{array}{cccc} & \mathbf{y} & \mathbf{x} 1 & \mathbf{x} 2 \\ \mathbf{x 1} & 0.816 & & \\ & 0.000 & & \\ \mathbf{x 2} & 0.413 & -0.144 & \\ & 0.029 & 0.466 & \\ \mathbf{x 3} & 0.768 & 0.588 & 0.406 \\ & 0.000 & 0.001 & 0.032\end{array}\)

Táblázat \(\PageIndex{1}\). Egy korrelációs mátrix.

Ebben a mátrixban a felső érték a lineáris korrelációs együttható, az alsó pedig a p-érték annak a nullhipotézisnek a tesztelésére, miszerint a korrelációs együttható nulla. Ez a mátrix lehetővé teszi számunkra, hogy megnézzük az egyes prediktor változók és a válaszváltozók közötti lineáris kapcsolat erősségét és irányát, de a prediktor változók közötti kapcsolatot is. Például y és x1 erős, pozitív lineáris kapcsolatban áll r = 0,816, ami statisztikailag szignifikáns, mert p = 0,000. Azt is láthatjuk, hogy az x1 és x3 prediktor változók mérsékelten erős pozitív lineáris kapcsolattal rendelkeznek (r = 0,588), ami jelentős (o = 0,001).

Számos oka van annak, hogy kiválasszuk, mely magyarázó változókat vegyük fel modellünkbe (lásd: Modellfejlesztés és kiválasztás), azonban gyakran választjuk azokat, amelyek magas lineáris korrelációt mutatnak a válaszváltozóval, de óvatosnak kell lennünk. Nem akarunk olyan magyarázó változókat belefoglalni, amelyek egymással erősen korrelálnak. Tisztában kell lennünk a prediktor változók közötti multikollinearitással.

A multicollinearitás két magyarázó változó között létezik, ha erős lineáris kapcsolatuk van.

Például, ha megpróbáljuk megjósolni egy személy vérnyomását, az egyik előrejelző változó a súly, a másik előrejelző változó pedig az étrend. Mindkét előrejelző változó erősen korrelál a vérnyomással (mivel a súly növeli a vérnyomást, és ahogy az étrend növeli a vérnyomást is). De mindkét prediktor változó szintén erősen korrelál egymással. Mindkét előrejelző változó lényegében ugyanazt az információt közvetíti, amikor a vérnyomás magyarázatáról van szó. Mindkettő bevonása a modellbe problémákat okozhat az együtthatók becslésekor, mivel a multikollinearitás növeli az együtthatók standard hibáit. Ez azt jelenti, hogy egyes változók együtthatói nem különböznek szignifikánsan a nullától, míg többkollinearitás nélkül és alacsonyabb standard hibák esetén ugyanazokat az együtthatókat lehetett szignifikánsnak találni. Ez a szöveg nem foglalkozik a multikollinearitás tesztelésének módjaival, azonban általános ökölszabály, hogy óvakodjunk a -0,7-nél kisebb és 0,7-nél nagyobb lineáris korrelációtól két előrejelző változó között. A multikollinearitási problémák elkerülése érdekében mindig vizsgálja meg a korrelációs mátrixot a prediktor változók közötti kapcsolatok szempontjából.

Becslés

A becslési és következtetési eljárások szintén nagyon hasonlítanak az egyszerű lineáris regresszióhoz. Ahogy mintaadatainkat felhasználtuk a becsléshez β0 és β1 egyszerű lineáris regressziós modellünkhöz, kiterjesztjük ezt a folyamatot a többszörös regressziós modelljeink összes együtthatójának becslésére.

Az egyszerűbb populációs modellel

\[\mu_y = \beta_0+\beta_1x\]

β1 a meredekség, és megmondja a felhasználónak, hogy mi lenne a válasz változása, amikor az előrejelző változó változik. Több prediktor változóval, és ezért több becslendő paraméterrel a β1, β2, β3 és így tovább együtthatókat részleges lejtéseknek vagy részleges regressziós együtthatóknak nevezzük. A részleges meredekség βi az y változását méri egy egységnyi változás esetén x én ha az összes többi független változót állandó értéken tartjuk. Ezeket a regressziós együtthatókat a mintaadatokból kell megbecsülni annak érdekében, hogy megkapjuk a becsült többszörös regressziós egyenlet általános formáját

\[\hat y = b_0+b_1x_1+b_2x_2+b_3x_3+...+b_kx_k\]

és a populációs modell

\[\mu_y = \beta_0 + \beta_1x_1+\beta_2x_2+\beta_3x_3+...+\beta_kx_k\]

ahol k = a független változók száma (más néven prediktor változók)

y= a függő változó előrejelzett értéke (a többszörös regressziós egyenlet segítségével számítva)

x 1, x 2,..., x k = a független változók

β0 az y-metszés (y értéke, ha az összes prediktor változó egyenlő 0)

b 0 a β0 becslése az adott mintaadatok alapján

β1, β2, β3,... βk az x 1, x 2,..., x k független változók együtthatói

b 1, b 2, b 3,..., b k a β1, β2, β3,... βk együtthatók mintapecslései

A legkisebb négyzetek módszerét továbbra is használják a modellnek az adatokhoz való illesztésére. Ne feledje, hogy ez a módszer minimalizálja a megfigyelt és előre jelzett értékek (SSE) négyzetes eltéréseinek összegét.

A többszörös regresszió varianciatáblázatának elemzése hasonló megjelenésű, mint egy egyszerű lineáris regresszióé.

A variáció forrása	df	Négyzetek szekvencia összegei	Négyzetek összegei	A négyzetek átlagos összege	F
Regresszió	k		SSR	SSR/k = MSR	MSR/MSE = F
Hiba	n - k - 1		SSE	SSE/ (n - k - 1) = MSE
Összesen	n -1		SST

Táblázat \(\PageIndex{2}\). ANOVA asztal.

Ahol k a prediktor változók száma és n a megfigyelések száma.

A véletlenszerű variáció legjobb becslése \(\sigma^2\) - a prediktor változók által megmagyarázhatatlan variáció - továbbra is s2, az MSE. A regressziós standard hiba, s, az MSE négyzetgyöke.

Az ANOVA táblázat új oszlopa a többszörös lineáris regresszióhoz az SSR bomlását mutatja, amelyben az egyes előrejelző változók feltételes hozzájárulása a modellbe már bevitt változók alapján a regresszióban megadott bejegyzési sorrendben jelenik meg. Ezek a feltételes vagy szekvenciális négyzetösszegek mindegyike 1 regressziós szabadságfokot jelent, és lehetővé teszi a felhasználó számára, hogy lássa az egyes előrejelző változók hozzájárulását a regressziós modell által magyarázott teljes variációhoz az arány használatával:

\[\dfrac {SeqSS}{SSR}\]

Korrigált \(R^2\)

Egyszerű lineáris regresszióban a magyarázott és a teljes variáció közötti kapcsolatot használtuk a modell illeszkedésének mérésére:

\[R^2 = \dfrac {Explained \ Variation}{Total \ Variation} = \dfrac {SSR}{SSTo} = 1 - \dfrac {SSE}{SSTo}\]

Ebből a definícióból vegye figyelembe, hogy a meghatározási együttható értéke soha nem csökkenhet több változó hozzáadásával a regressziós modellbe. Ezért mesterségesen \(R^2\) felfújható, mivel több változó (szignifikáns vagy sem) szerepel a modellben. A regressziós modell alternatív erősségi mértékét a szabadságfokokhoz igazítják úgy, hogy az átlagos négyzeteket használják, nem pedig a négyzetek összegét:

\[R^2(adj) = 1 -\dfrac {(n-1)(1-R^2)}{(n-p)} = (1 - \dfrac {MSE}{SSTo/(n-1)})\]

A korrigált \(R^2\) érték a válaszváltozó változóinak százalékos arányát jelenti, amelyet a független változók magyaráznak, korrigálva a szabadságfokokkal. Ellentétben\(R^2\), a kiigazított nem \(R^2\) fog növekedni a változók hozzáadásakor, és hajlamos stabilizálódni valamilyen felső határ körül a változók hozzáadásakor.

Jelentőségi tesztek

Emlékezzünk vissza az előző fejezetben, amelyet teszteltünk, hogy y és x lineárisan kapcsolódnak-e egymáshoz teszteléssel

\(H_0: \beta_1 = 0\)

\(H_1: \beta_1 \ne 0\)

a t-próbával (vagy azzal egyenértékű F-próbával). Többszörös lineáris regresszióban több részleges lejtés van, és a t-teszt és az F-teszt már nem egyenértékű. Kérdésünk megváltozik: Jobb-e az a regressziós egyenlet, amely az x1, x2, x3,..., xk prediktor változók által szolgáltatott információkat használja, mint az egyszerű prediktor (az átlagos válaszérték), amely nem támaszkodik ezekre a független változókra?

\(H_0: \beta_1 = \beta_2 = \beta_3 = …=\beta_k = 0\)

\(H1: At \ least \ one \ of β_1, β_2 , β_3 , …β_k \ne 0\)

Az F-teszt statisztikáját használják erre a kérdésre, és megtalálható az ANOVA táblázatban.

\[F=\dfrac{MSR}{MSE}\]

Ez a tesztstatisztika követi az F-eloszlást és. \(df_1 = k\) \(df_2 = (n-k-1)\) Mivel a pontos p-érték a kimenetben van megadva, a döntési szabály segítségével válaszolhat a kérdésre.

Ha a p-érték kisebb, mint a szignifikancia szintje, utasítsa el a nullhipotézist.

A nullhipotézis elutasítása alátámasztja azt az állítást, hogy a prediktor változók közül legalább az egyik szignifikáns lineáris kapcsolatban áll a válaszváltozóval. A következő lépés annak meghatározása, hogy mely prediktor változók adnak fontos információkat az előrejelzéshez a modellben már szereplő többi előrejelző jelenlétében. A részleges regressziós együtthatók jelentőségének teszteléséhez minden összefüggést külön kell megvizsgálnia egyedi t-tesztek segítségével.

\(H_0: β_i = 0\)

\(H_1: β_i \ne 0\)

\[t=\dfrac {b_i-\beta_o}{SE(b_i)} \ with \ df = (n-k-1)\]

ahol SE (b _i) a b _i standard hibája. Pontos p-értékeket is megadunk ezekhez a tesztekhez. Az egyes előrejelző változók specifikus p-értékeinek vizsgálata lehetővé teszi annak eldöntését, hogy mely változók kapcsolódnak szignifikánsan a válaszváltozóhoz. Általában minden jelentéktelen változót eltávolítanak a modellből, de ne feledje, hogy ezeket a teszteket a modell más változóival végzik. Jó eljárás a legkevésbé jelentős változó eltávolítása, majd a modell visszaállítása a csökkentett adatkészlettel. Minden új modellnél mindig ellenőrizze a regressziós standard hibát (az alacsonyabb jobb), a korrigált R ² (magasabb jobb), a p-értékek az összes prediktor változóhoz, valamint a maradék és normál valószínűségi ábrák.

A számítások összetettsége miatt szoftverre támaszkodunk, hogy illeszkedjen a modellhez, és megadja nekünk a regressziós együtthatókat. Ne felejtsd el... mindig szétszórt parcellákkal kezded. A prediktor és a válaszváltozók közötti erős kapcsolatok jó modellt eredményeznek.

Példa \(\PageIndex{1}\):

Egy kutató adatokat gyűjtött egy projekt során, hogy megjósolja a hegyvidéki boreális erdők hektáronkénti éves növekedését Kanada déli részén. Feltételezték, hogy a köbméter térfogatának növekedése (y) az állomány alapterületének hektáronkénti függvénye (x 1), az alapterület százalékos aránya a fekete lucfenyőben (x 2), és az állvány helyének indexe a fekete lucfenyő esetében (x 3). α = 0,05.

CUFT	BA/AC	%BA Bluc	SI		CUFT	BA/AC	%BA Bluc	SI
55	51	79	45		71	65	93	35
68	100	48	53		67	87	68	41
60	63	67	44		73	108	51	54
40	52	52	31		87	105	82	51
45	67	52	29		80	100	70	45
49	42	82	43		77	103	61	43
62	81	80	42		64	55	96	51
56	70	65	36		60	60	80	47
93	108	96	63		65	70	76	40
76	90	81	60		65	78	74	46
94	110	78	56		83	85	96	55
82	111	59	48		67	92	58	50
86	94	84	53		61	82	58	38
55	82	48	40		51	56	69	35

Táblázat \(\PageIndex{3}\). Megfigyelt adatok a köbméterről, az állvány alapterületéről, a fekete lucfenyő alapterületének százalékos alapterületéről és a helyszín indexéről.

A válaszváltozó szórásdiagramjait az egyes prediktor változókkal szemben egy korrelációs mátrixszal együtt hoztuk létre.

Ábra \(\PageIndex{1}\). A köbláb és az alapterület szórása, a fekete lucfenyő alapterületének százalékos aránya és a helyszín indexe.

 

 

\ [\ begin {array} {l}
\ text {Összefüggések: CUft, BA/ac, %BA Bspruce, SI}\
\ kezdés {array} {|c|c|c|c|c|c|c|}}
\ hline\ mathrm {BA}/\ mathrm {ac} &\ begin {array}\ text {CUft}\\
0.816\
0.000\\ vége {array} &
\ mathrm {BA}/\ mathrm {aC} &\ frac {8} {8}
\ mathrm {BA} &\ text {Bspruce}\\\ hline\ text {A Bspruce} &\ kezdet {array} {l} 0.413\\ 0.029\ vége {array} &\ kezdő {array} {r}




-0.144\\
0.466
\ vége {array} & &\\\ hline
\ text {SI} &\ kezdő {array} {l}
0.768\\
0.000\ vége {array} &
\ kezdet {array} {l}
0.588\\
0.001
\ vége {tömb} &\ kezdődik {array} {l}
0.406\\
0.032\ vég {array}\\ hline\ vége {array}
\ vége {array}\]

Táblázat \(\PageIndex{4}\). Korrelációs mátrix.

Amint az a szórásdiagramokból és a korrelációs mátrixból látható, a BA/ac a legerősebb lineáris kapcsolatban áll a CuFT térfogatával (r = 0,816) és %BA fekete lucfenyőben a leggyengébb lineáris kapcsolat (r = 0,413). Szintén figyelemre méltó a mérsékelten erős korreláció a két prediktor változó, a Ba/ac és az SI között (r = 0,588). Mindhárom prediktor változó szignifikáns lineáris kapcsolatban áll a válaszváltozóval (térfogat), ezért a többszörös lineáris regressziós modellünk összes változójának felhasználásával kezdjük. A Minitab kimenet az alábbiakban látható.

Kezdjük a következő null- és alternatív hipotézisek tesztelésével:

H ₀: β ₁ = β ₂ = β ₃ = 0

H ₁: A β ₁, β ₂, β ₃ ≠ 0 közül legalább egy

Általános regressziós elemzés: CuFT versus Ba/ac, SI, %BA Bspruce

 

Regressziós egyenlet: CuFT = -19,3858 + 0,591004 BA/ac + 0,0899883 SI + 0,489441 %BA Bspruce

együtthatók
Kifejezés	Coef	SE Coef	T	P	95% CI
Állandó	-19.3858	4.15332	-4.6675	0.000	(-27,9578, -10.8137)
BA/AC	0.5910	0.04294	13.7647	0.000	(0,5024, 0,6796)
SI	0.0900	0.11262	0.7991	0.432	(-0,1424, 0,3224)
%BA Bluc	0.4894	0.05245	9.3311	0.000	(0.3812, 0.5977)
Model rész összegzése
S = 3.17736		R-Sq = 95,53%		R-Sq (adj) = 94,97%
NYOMJA MEG = 322.279		R-Sq (pred) = 94,05%
Varianciaanalízis
Forrás	DF	SS Seq	Adj SS	Adj MS	F	P
Regresszió	3	5176.56	5176.56	1725.52	170.918	0.000000
BA/AC	1	3611.17	1912.79	1912.79	189.467	0.000000
SI	1	686.37	6.45	6.45	0.638	0.432094
%BA Bluc	1	879.02	879.02	879.02	87.069	0.000000
Hiba	24	242.30	242.30	10.10
Összesen	27	5418.86

Az F-teszt statisztikája (és a hozzá tartozó p-érték) a kérdés megválaszolására szolgál, és megtalálható az ANOVA táblázatban. Ebben a példában F = 170,918 0,00000 p-értékkel. A p-érték kisebb, mint a szignifikancia szintünk (0,0000<0,05), ezért elutasítjuk a nullhipotézist. A prediktor változók közül legalább az egyik jelentősen hozzájárul a térfogat előrejelzéséhez.

A három előrejelző változó együtthatói mind pozitívak, jelezve, hogy a köbméter növekedésével a térfogat is növekedni fog. Például, ha SI és %BA Bspruce állandó értékeket tartunk, ez az egyenlet azt mondja nekünk, hogy ahogy az alapterület 1 négyzetméterrel növekszik. ft., a térfogat további 0,591004 cu. ft. Ezeknek az együtthatóknak a jelei logikusak, és mire számíthatunk. A korrigált R ² szintén nagyon magas, 94,97%.

A következő lépés az egyes t-tesztek vizsgálata minden előrejelző változóhoz. A vizsgálati statisztikák és a kapcsolódó p-értékek a Minitab kimenetben találhatók, és az alábbiakban megismétlődnek:

együtthatók
Kifejezés	Coef	SE Coef	T	P	95% CI
Állandó	-19.3858	4.15332	-4.6675	0.000	(-27,9578, -10.8137)
BA/AC	0.5910	0.04294	13.7647	0.000	(0,5024, 0,6796)
SI	0.0900	0.11262	0.7991	0.432	(-0,1424, 0,3224)
%BA Bluc	0.4894	0.05245	9.3311	0.000	(0.3812, 0.5977)

A Ba/ac és %BA Bspruce előrejelző változók t-statisztikája 13,7647 és 9.3311 és p-értéke 0,0000, ami azt jelzi, hogy mindkettő jelentősen hozzájárul a térfogat előrejelzéséhez. Az SI azonban t-statisztikája 0,7991, p-értéke 0,432. Ez a változó nem járul hozzá jelentősen a köbméter térfogatának előrejelzéséhez.

Ez az eredmény meglephet, mivel az SI -nek volt a második legerősebb kapcsolata a térfogattal, de ne feledkezzen meg az SI és a Ba/ac közötti korrelációról (r = 0,588). A Ba/ac előrejelző változónak volt a legerősebb lineáris kapcsolata a térfogattal, és a szekvenciális négyzetösszegek felhasználásával láthatjuk, hogy a Ba/ac már a köbméter térfogat változásának 70% -át teszi ki (3611.17/5176.56 = 0,6976). Az SI információi túlságosan hasonlóak lehetnek a Ba/ac információkhoz, és az SI csak a térfogat változásának körülbelül 13% -át magyarázza (686,37/5176,56 = 0,1326), tekintettel arra, hogy a Ba/ac már szerepel a modellben.

A következő lépés a maradék és a normál valószínűségi diagramok vizsgálata. Egyetlen kiugró érték nyilvánvaló az egyébként elfogadható parcellákon.

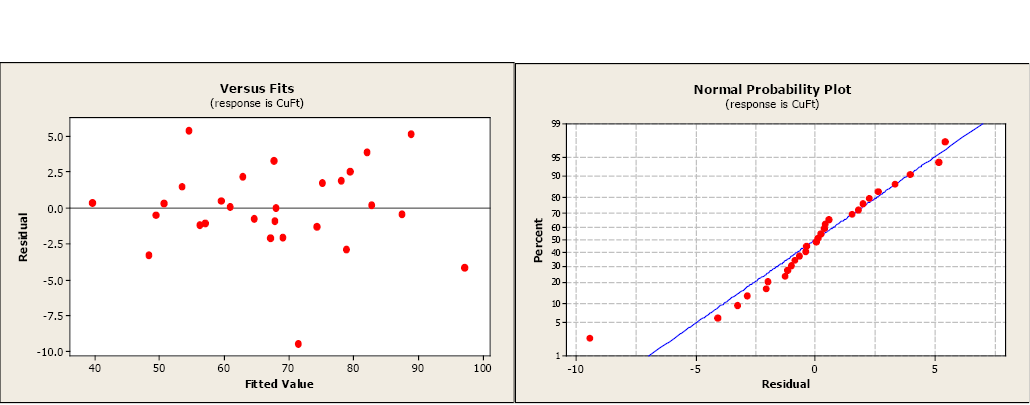
Ábra \(\PageIndex{2}\). Maradék és normál valószínűségi diagramok.

Szóval, hová megyünk innen?

Eltávolítjuk a nem szignifikáns változót, és újra illesztjük a modellt, kivéve az SI adatait a modellünkben. A Minitab kimenet az alábbiakban látható.

Általános regressziós elemzés: CuFT versus Ba/ac, %BA Bspruce

Regressziós egyenlet
CUft = -19 1142 + 0,615531 BA/ac + 0,515122 %BA Bluc
együtthatók
Kifejezés	Coef	SE Coef	T	P	95% CI
Állandó	-19.1142	4.10936	-4.6514	0.000	(-27,5776, -10.6508)
BA/AC	0.6155	0.02980	20.6523	0.000	(0,5541, 0.6769)
%BA Bluc	0.5151	0.04115	12.5173	0.000	(0,4304, 0,5999)
Model rész összegzése
S = 3.15431		R-Sq = 95,41%		R-Sq (adj) = 95,04%
NYOMJA MEG = 298.712		R-Sq (pred) = 94,49%
Varianciaanalízis
Forrás	DF	SeqSS	ADJS-ek	ADJM-ek	F	P
Regresszió	2	5170.12	5170.12	2585.06	259.814	0.0000000
BA/AC	1	3611.17	4243,71	4243,71	426.519	0.0000000
%BA Bluc	1	1558.95	1558.95	1558.95	156.684	0.0000000
Hiba	25	248.74	248.74	9.95
Összesen	27	5418.86

Megismételjük az első modellünkkel követett lépéseket. Kezdjük a következő hipotézisek újbóli tesztelésével:

\(H_0: \beta_1 = \beta_2 = \beta_3 = 0\)

\(H_1: At \ least \ one \ of \ \beta_1, \beta_2 , \beta_3 \ne 0\)

Ennek a csökkentett modellnek F-statisztikája 259,814 és p-értéke 0,0000. Elutasítjuk a nullhipotézist. A prediktor változók közül legalább az egyik jelentősen hozzájárul a térfogat előrejelzéséhez. Az együtthatók továbbra is pozitívak (ahogy vártuk), de az értékek megváltoztak, hogy figyelembe vegyék a különböző modellt.

Az egyes t-tesztek minden együtthatóra (alább megismételve) azt mutatják, hogy mindkét prediktor változó jelentősen eltér a nullától, és hozzájárul a térfogat előrejelzéséhez.

együtthatók
Kifejezés	Coef	SE Coef	T	P	95% CI
Állandó	-19.1142	4.10936	-4.6514	0.000	(-27,5776, -10.6508)
BA/AC	0.6155	0.02980	20.6523	0.000	(0,5541, 0.6769)
%BA Bluc	0.5151	0.04115	12.5173	0.000	(0,4304, 0,5999)

Figyeljük meg, hogy a korrigált R2 94.97% -ról 95,04% -ra nőtt, ami valamivel jobban illeszkedik az adatokhoz. A regressziós standard hiba is jobbra változott, 3.17736-ról 3.15431-re csökkent, ami a megfigyelt adatok kissé kisebb eltérését jelzi a modellhez képest.

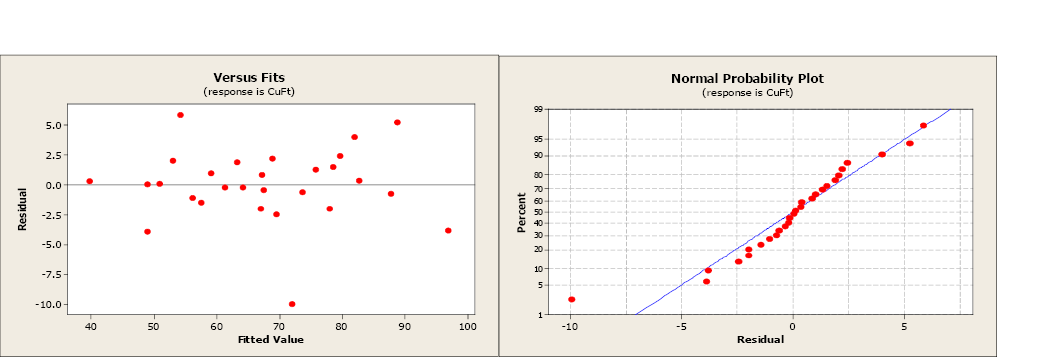
Ábra \(\PageIndex{3}\). Maradék és normál valószínűségi diagramok.

A maradék és a normál valószínűségi diagramok alig változtak, még mindig nem jeleztek problémákat a regressziós feltételezéssel kapcsolatban. A nem szignifikáns változó eltávolításával a modell javult.