6.2: Többszörös összehasonlítások

Last updated
Save as PDF

Page ID: 205344

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

A következő lépés az egyes fő hatások többszörös összehasonlításának vizsgálata a különbségek meghatározása érdekében. Úgy járunk el, mint az egyirányú ANOVA többszörös összehasonlításokkal, megvizsgálva a Tukey csoportosítását az egyes fő hatásokhoz. Az A faktor esetében a fajta, a mintaátlagok és a csoportosító betűk kerülnek bemutatásra, hogy azonosítsák azokat a fajtákat, amelyek jelentősen különböznek a többi fajtától. Az 1. és 2. fajta nem különbözik szignifikánsan egymástól, mindkettő hasonló hozamot eredményez. A 3. fajta szignifikánsan nagyobb hozamot produkált, mint az 1. és a 2. fajta.

Információk csoportosítása Tukey-módszerrel és 95,0% -os bizalom

fajta	N	Átlag	Csoportosítás
3	12	18.117	A
2	12	12.208		B
1	12	11.317		B
Azok az eszközök, amelyek nem osztják meg a levelet, jelentősen különböznek egymástól.

A sűrűségek egy része szintén jelentősen eltér. Ugyanezt az eljárást fogjuk követni a különbségek meghatározására.

Információk csoportosítása Tukey-módszerrel és 95,0% -os bizalom

sűrűség	N	Átlag	Csoportosítás
15	9	15.756	A
10	9	14.389	A	B
20	9	13.922		B
5	9	11.456			C
Azok az eszközök, amelyek nem osztják meg a levelet, jelentősen különböznek egymástól.

A csoportosítási információk azt mutatják, hogy a 15 000 növény/parcella ültetési sűrűsége a legnagyobb hozamot eredményezi. A terméshozamban azonban nincs szignifikáns különbség 10 000 és 15 000 növény/telek, vagy 10 000 és 20 000 növény/telek között. Az 5000 növény/parcellával rendelkező parcellák a legalacsonyabb hozamot eredményezik, és ezek a hozamok lényegesen alacsonyabbak, mint az összes többi vizsgált sűrűség.

A fő hatásábrák a három fajta és a négy sűrűség hozambeli különbségeit is szemléltetik.

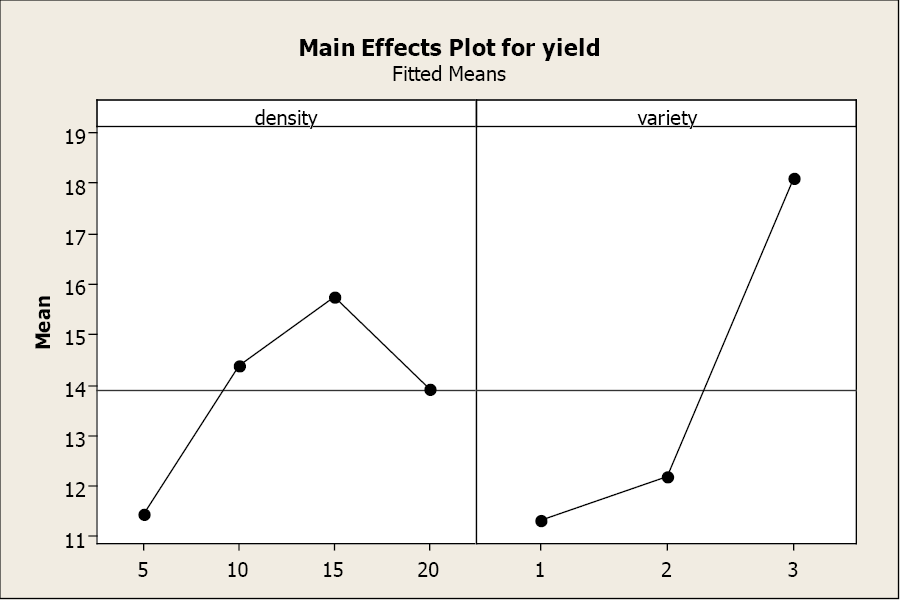
Mi a 9662.png — Ábra\(\PageIndex{1}\): Fő hatások ábrák.

De mi történik, ha jelentős kölcsönhatás van a fő hatások között? Ez a következő példa bemutatja, hogy egy jelentős interakció hogyan változtatja meg a kétirányú ANOVA értelmezését.

Példa \(\PageIndex{1}\):

Egy kutatót négy műtrágyázási szint (kontroll, 100 font, 150 font és 200 font) és négy öntözési szint (A, B, C és D) hatása érdekelt a biomassza hozamára. A tizenhat lehetséges kezelési kombinációt véletlenszerűen 80 parcellához rendelték (5 parcella minden kezeléshez). Az egyes kezelések teljes biomassza-hozamát az alábbiakban soroljuk fel.

		Műtrágya
Öntözés	Ellenőrzés	100 lb.	150 lb.	200 lb.
A	2700,2801 2720, 2390, 2890	3250, 3151, 3170, 3300, 3290	3300, 3235, 3025, 3165, 3120	3500, 3455, 3100, 3600, 3250
B	3101, 3035, 3205, 3007, 3100	2700, 2935, 2250, 2495, 2850	3050, 3110, 3033, 3195, 4250	3100, 3235, 3005, 3095, 3050
C	101, 97, 106, 142, 99	400, 302, 296, 315, 390	630, 624, 595, 675, 595	400, 325, 200, 375, 390
D	121, 174, 88, 100, 76	100, 125, 91, 222, 219	60, 28, 112, 89, 67	201, 223, 195, 120, 180

Táblázat 6. Megfigyelt adatok négy öntözési szintre és négy műtrágyaszintre vonatkozóan.

Az A faktor (öntözési szint) k = 4, a B faktor (műtrágya) pedig l = 4 szint. Vannak m = 5 ismétlés és összesen 80 megfigyelés. Ez egy kiegyensúlyozott kialakítás, mivel az ismétlések száma egyenlő. Az ANOVA táblázatot a következőkben mutatjuk be.

Kétirányú ANOVA asztal.

Forrás	DF	SS	MSS	F	P
trágya	3	1128272	376091	12.76	<0,001
öntözés	3	161776127	53925376	1830,16	<0,001
fert*öntözés	9	2088667	232074	7.88	<0,001
hiba	64	1885746	29465
teljes	79	166878812

Ismét az interakciós kifejezés tesztelésével kezdjük. Ne feledje, hogy ha az interakciós kifejezés jelentős, figyelmen kívül hagyjuk a fő hatásokat.

\(H_0\): Nincs kölcsönhatás a tényezők között

\(H_1\): Jelentős kölcsönhatás van a tényezők között

Az F-statisztika:

\[F_{AB} = \dfrac {MSAB}{MSE} = \dfrac {232074}{29465} = 7.88 \nonumber \]

A tényezők közötti szignifikáns kölcsönhatás tesztjének p-értéke <0,001. Ez a p-érték kevesebb, mint 5%, ezért elutasítjuk a nullhipotézist. Bizonyíték van a műtrágya és az öntözés közötti jelentős kölcsönhatásra. Mivel az interakciós kifejezés jelentős, nem vizsgáljuk a fő hatások jelenlétét. Most meg kell vizsgálnunk mind a 16 kezelés többszörös összehasonlítását (a műtrágya és az öntözési szint minden kombinációja), hogy meghatározzuk a hozamkülönbségeket, a faktordiagram segítségével.

Információk csoportosítása Tukey-módszerrel és 95,0% -os bizalom

fert	öntözés	N	Átlag	Csoportosítás
200	A	5	3381.00	A
150	B	5	3327.60	A
100	A	5	3232.20	A
150	A	5	3169.00	A
200	B	5	3097.00	A
C	B	5	3089.60	A
C	A	5	2700.20		B
100	B	5	2646.00		B
150	C	5	623.80			C
100	C	5	340.60			C	D
200	C	5	338.00			C	D
200	D	5	183.80				D
100	D	5	151.40				D
C	D	5	111.80				D
C	C	5	109.00				D
150	D	5	71.20				D
Azok az eszközök, amelyek nem osztják meg a levelet, jelentősen különböznek egymástól.

A faktordiagram lehetővé teszi a 16 kezelés közötti különbségek megjelenítését. A faktordiagramok kétféleképpen mutathatják be az információt, mindegyik eltérő tényezővel rendelkezik az x tengelyen. Az első parcellában a műtrágya szintje az x tengelyen van. Világos különbség van a különböző kezelések átlagos hozamában. Úgy tűnik, hogy az A és B öntözési szint nagyobb hozamot eredményez a műtrágyák minden szintjén, mint a C és D öntözési szint. A második parcellán az öntözési szint az x tengelyen van. Úgy tűnik, hogy a műtrágya minden szintje nagyobb hozamot eredményez az A és B öntözési szinteknél, mint a C és D.

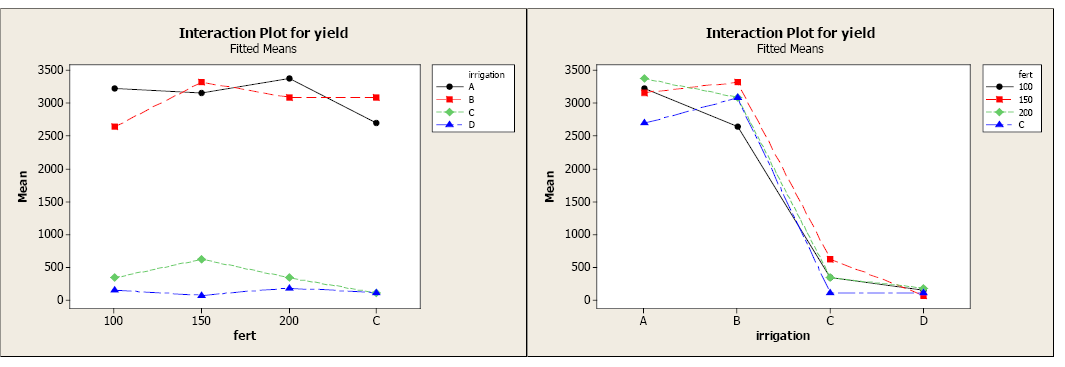
Mi a 9631.png — Ábra\(\PageIndex{2}\): Interakciós parcellák.

A következő lépés a többszörös összehasonlító kimenet használata annak meghatározására, hogy hol vannak JELENTŐS különbségek. Koncentráljunk az első tényezőre, hogy ezt megtegyük.

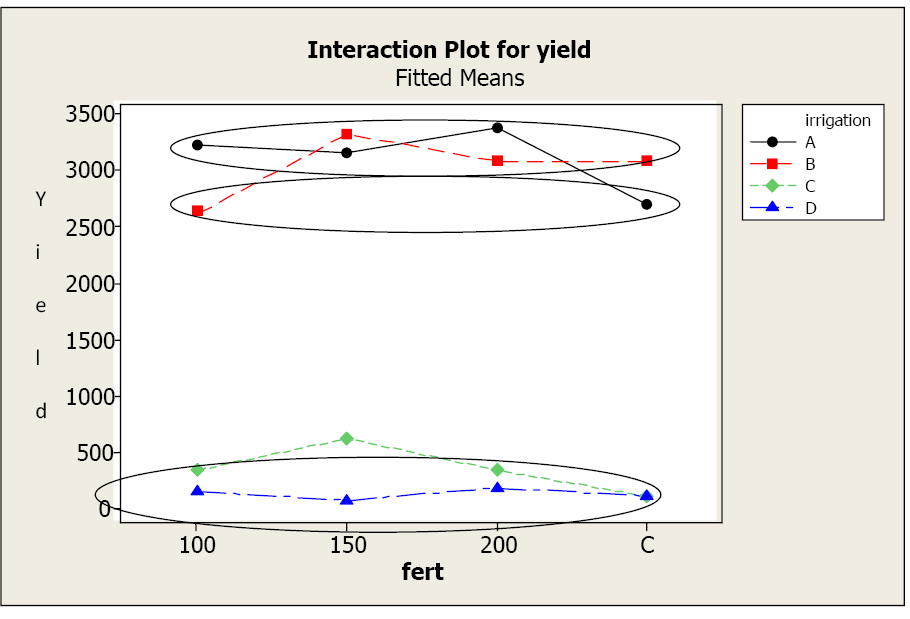
Mi a 9620.png — *Ábra\(\PageIndex{3}\): Interakciós diagram.*

A csoportosítási információk azt mutatják, hogy bár az A és B öntözési szintek hasonlóak a műtrágya minden szintjén, csak az A-100, A-150, A-200, B-kontroll, B-150 és B-200 kezelések statisztikailag hasonlóak (felső kör). A B-100 és A-kontroll kezelés szintén hasonló hozamokat eredményez (középső kör), és mindkettő szignifikánsan alacsonyabb hozammal rendelkezik, mint az első csoport.

A C és D öntözési szint a legalacsonyabb hozamot eredményezi a műtrágyaszintek között. A különbségek azonosításához ismét a csoportosítási információkra hivatkozunk. A D öntözési szint hozamában nincs szignifikáns különbség a műtrágya bármely szintjéhez képest. A D hozama is hasonló a C öntözési szint 100, 200 -as hozamához és a műtrágya szabályozási szintjéhez (legalacsonyabb kör). A C öntözési szint 150 szintű műtrágyánál szignifikánsan magasabb hozamot eredményez, mint bármely D öntözési szintből származó hozam bármely műtrágyaszintnél, azonban ez a hozam még mindig lényegesen kisebb, mint az első A és B öntözési szintet alkalmazó csoport.

Faktordiagramok értelmezése

Ha az interakciós kifejezés jelentős, az elemzés kizárólag a kezelésekre összpontosít, nem pedig a fő hatásokra. A faktordiagram és a csoportosítási információk lehetővé teszik a kutató számára, hogy azonosítsa a hasonlóságokat és különbségeket, valamint bármilyen trendet vagy mintát. A következő faktorábrák néhány valódi átlagos választ mutatnak be az interakciók és a fő hatások tekintetében.

Ez az első ábra egyértelműen jelentős kölcsönhatást mutat a tényezők között. A válasz változása, amikor a B szint változik, az A szinttől függ.

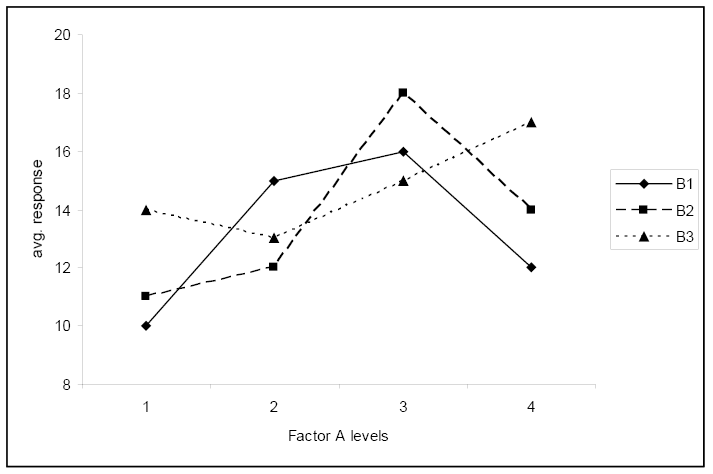
Mi a 9609.png

5. ábra.

A második ábra nem mutat jelentős kölcsönhatást. Az A faktor szintjére adott válaszváltozás a B faktor minden szintjén azonos.

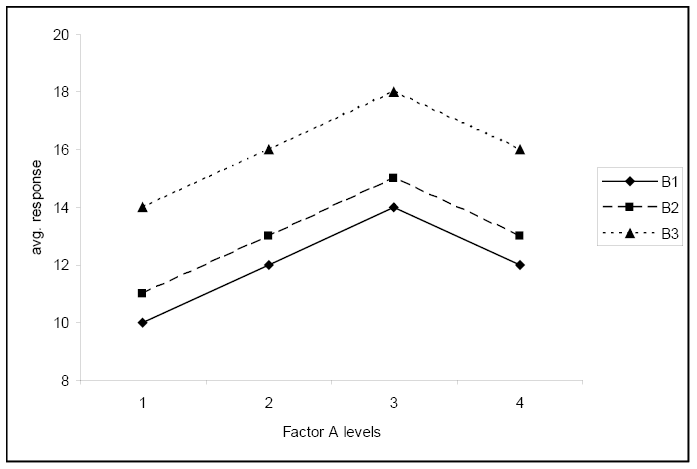
Mi a 9598.png — Ábra\(\PageIndex{5}\): Ábra\(\PageIndex{4}\): Interakciós diagram.

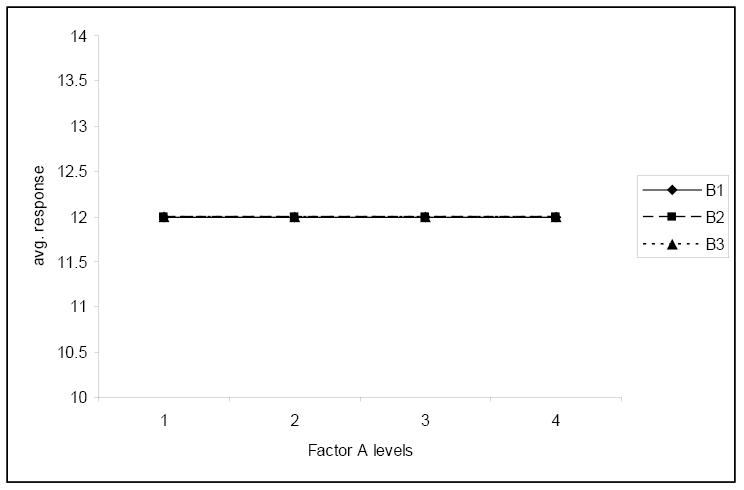
A harmadik ábra nem mutat szignifikáns kölcsönhatást, és azt mutatja, hogy az átlagos válasz nem függ az A tényező szintjétől.

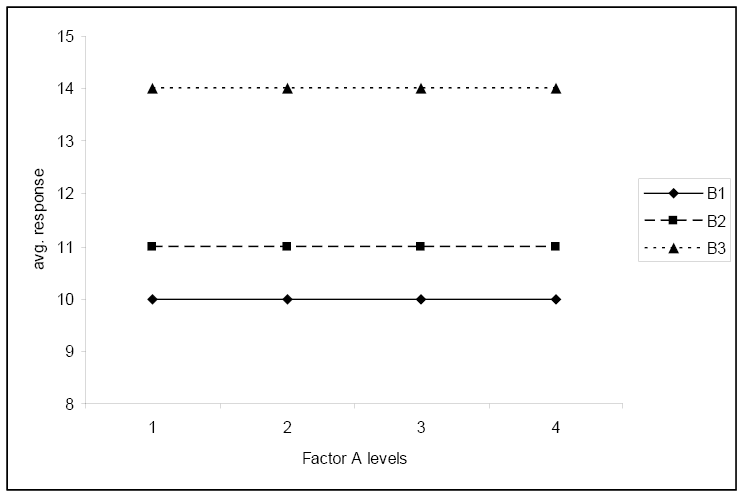
Mi a 9588.png — Ábra\(\PageIndex{6}\): Ábra\(\PageIndex{4}\): Interakciós diagram.

Ez a negyedik ábra ismét nem mutat szignifikáns kölcsönhatást, és azt mutatja, hogy az átlagos válasz nem függ a B faktor szintjétől.

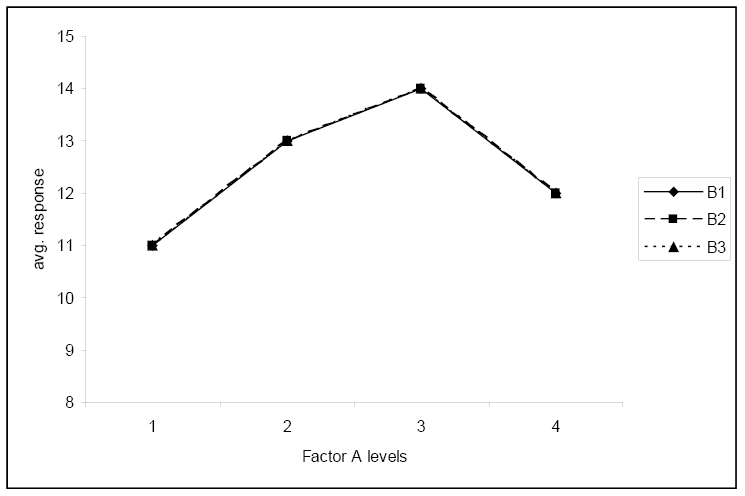
Mi a 9579.png — Ábra\(\PageIndex{7}\): Ábra\(\PageIndex{4}\): Interakciós diagram.

Ez az utolsó ábra nem szemlélteti az interakciót, és egyik tényező sem befolyásolja a választ.

Mi a 9568.png — Ábra\(\PageIndex{8}\): Ábra\(\PageIndex{4}\): Interakciós diagram.