3.5: Hipotézis teszt egy varianciáról

Last updated
Save as PDF

Page ID: 205322

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hipotézis teszt egy varianciáról

Amikor az emberek statisztikai következtetésekre gondolnak, általában a népesség átlagát vagy arányait érintő következtetésekre gondolnak. A kísérletező gyakorlati kérdéseinek megválaszolásához szükséges populációs paraméter azonban helyzetenként változik, és néha a populáció változékonysága fontosabb, mint az átlag. Így a termékminőséget gyakran az alacsony variabilitás alapján határozzák meg.

A minta varianciája $s^2$felhasználható a populáció varianciájára vonatkozó következtetésekre. $\sigma^2$ Véletlenszerű minta esetén n mérések normál populációból, átlagos μ és varianciával $\sigma^2$, az érték pontbecslést $s^2$ad a $\sigma^2$. Ezenkívül a mennyiség Chi-négyzet ($\chi^{2}$) eloszlást $\frac {(n-1)s^2}{\sigma^2}$ követ, val vel. $df = n – 1$

A Chi-négyzet ($\chi^{2}$) eloszlás tulajdonságai:

Ellentétben Z és t eloszlások, a khi-négyzet eloszlás értékei mind pozitívak.
A khi-négyzet eloszlás aszimmetrikus, ellentétben a Z és t eloszlással.
Sok chi-négyzet eloszlás létezik. Egy adott értéket kapunk a minta $s^2$varianciáihoz $(df = n – 1)$ kapcsolódó szabadságfokok meghatározásával.

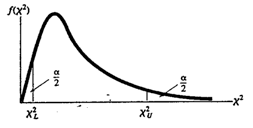
Mi a Image36711.PNG — Ábra$\PageIndex{1}$: A khi-négyzet eloszlás.

Egymintás ($\chi^{2}$) teszt a hipotézisek tesztelésére:

Nullhipotézis: $H_0: \sigma^{2} = \sigma^{2}_{0}$ (állandó)

Alternatív hipotézis:

$H_a: σ^2 > \sigma_{0}^{2}$(egyfarkú), utasítsa el, $H_0$ ha a megfigyelt $\chi^2 > \chi_{U}^{2}$ (felső farok értéke α).
$H_a: σ^2 <\sigma_{0}^{2}$(egyfarkú), utasítsa el, $H_0$ ha a megfigyelt $\chi^2 < \chi_{L}^{2}$ (alsó farok értéke α).
$H_a: σ^2 ≠ \sigma_{0}^{2}$(kétfarkú), utasítsa el, $H_0$ ha a megfigyelt $\chi^2 > \chi_{U}^{2}$ vagy $\chi^{2} < \chi_{L}^{2}$ α/2.

ahol az elutasítási régió $\chi^2$kritikus értéke a szabadságfokokon $df = n – 1$ és az α meghatározott szignifikanciaszintjén alapul.

Tesztstatisztika: $$\ chi^2 =\ frac {(n-1) S ^ 2} {\ sigma _ {0} ^ {2}}\]

Az előző szakaszokhoz hasonlóan, ha a tesztstatisztika a kritikus érték által beállított elutasítási zónába esik, akkor elutasítja a nullhipotézist.

Példa $\PageIndex{1}$:

Az erdész egy sűrű csíkos juhar aljnövényzetét akarja ellenőrizni, amely zavarja a keményfa kívánatos regenerálódását egy ködfúvóval, hogy gyomirtó kezelést alkalmazzon. Biztosítani akarja, hogy a kezelés egyenletes alkalmazási arányú legyen, vagyis alacsony variabilitás nem haladja meg a 0,25 gal értéket. /hektár (0,06 gal.2). Mintaadatokat gyűjt (n = 11) az ilyen típusú ködfúvón, és 0,064 gal.2 minta varianciát kap.2 5% -os szignifikanciaszint használatával tesztelje azt az állítást, hogy a szórás szignifikánsan nagyobb, mint 0,06 gal.2

$H_0: \sigma^{2} = 0.06$

$H_1: \sigma^{2} >0.06$

A kritikus érték 18.307. Bármely, ennél az értéknél nagyobb tesztstatisztika elutasítja a nullhipotézist.

A teszt statisztikája

\[\chi^2 = \frac {(n-1)S^2}{\sigma_{0}^{2}}=\frac {(11-1)0.064}{0.06}=10.667 \nonumber \]

Nem utasítjuk el a nullhipotézist. Az erdésznek NEM van elegendő bizonyítéka annak alátámasztására, hogy a szórás nagyobb, mint 0,06 gal.2 A p-értéket ugyanazzal a módszerrel is megbecsülheti, mint a hallgatói t-táblázat esetében. Menjen át a sorban a szabadságfokokért, amíg meg nem találja azt a két értéket, amelyek közé a tesztstatisztika esik. Ebben az esetben a 10. sorban haladva a két táblázat értéke 4,865 és 15.987. Most menjen fel a két oszlopra a felső sorba, hogy megbecsülje a p-értéket (0,1-0,9). A p-érték nagyobb, mint 0,1 és kevesebb, mint 0,9. Mindkettő nagyobb, mint a szignifikancia szintje (0,05), ami miatt nem utasítjuk el a nullhipotézist.

Szoftver megoldások

Minitab

(hivatkozva az Ex. $\PageIndex{1}$)

Mi a 067_1.tif

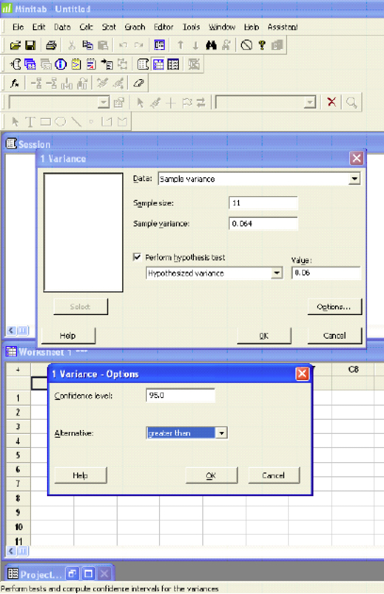
Mi a 067_2.tif

Teszt és CI egy varianciára

Módszer
Null hipotézis	Sigma-négyzet	= 0.06
Alternatív hipotézis	Sigma-négyzet	> 0.06

A khi-négyzet módszer csak a normál eloszlásra vonatkozik.

Vizsgálatok

Teszt
Módszer	Statisztika	DF	P-érték
Chi-tér	10.67	10	0.384

Excel

Az Excel nem kínál 1 minta $\chi^2$tesztelést.