3.1: A hipotézis tesztelésének alapjai

Last updated
Save as PDF

Page ID: 205315

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Az előző két fejezet bevezette a mintaadatok rendszerezésének és összegzésének módszereit, valamint a minta statisztikák felhasználását a populáció paramétereinek becslésére. Ez a fejezet bemutatja a következtetési statisztikák következő fő témáját: a hipotézis tesztelését.

Megjegyzés

A hipotézis egy állítás vagy állítás egy lakosság tulajdonáról.

A hipotézis tesztelésének alapjai

A tudományos kutatás során jellemzően van néhány ismert információ, talán valamilyen korábbi munkából vagy egy régóta elfogadott ötletből. Meg akarjuk vizsgálni, hogy ez az állítás hihető-e. Ez a hipotézis teszt alapgondolata:

Mondja el, amit igaznak gondolunk.
Számszerűsítse, mennyire bízunk az állításunkban.
Használja a minta statisztikákat, hogy következtetéseket vonjon le a populáció paramétereiről.

Például a korábbi kutatások azt mondják, hogy a kolibri átlagos élettartama körülbelül négy év. Tanulmányozta a kolibrit az Egyesült Államok délkeleti részén, és a minta átlagos élettartama 4,8 év. El kell utasítania az ismert vagy elfogadott információkat az eredmények javára? Mennyire bízik a becslésében? Mikor mondaná, hogy elegendő bizonyíték áll rendelkezésre az ismert információk elutasításához és az alternatív állítás alátámasztásához? Mennyire lehet messze az ismert négyéves átlagtól a minta, mielőtt elutasítanánk azt az elképzelést, hogy a kolibri átlagos élettartama négy év?

Meghatározás: hipotézis tesztelés

A hipotézis tesztelés egy eljárás, minta bizonyítékain és valószínűségén alapul, amelyet a populáció jellemzőire vonatkozó állítások tesztelésére használnak.

A hipotézis egy állítás vagy állítás a számunkra érdekes populáció jellemzőiről. A hipotézis teszt egy módja annak, hogy minta statisztikáinkat felhasználjuk egy adott állítás tesztelésére.

Példa \(\PageIndex{1}\):

A populáció átlagos súlya ismert, hogy 157 font, tesztelni akarjuk azt az állítást, hogy az átlagos súly nőtt.

Példa \(\PageIndex{2}\):

Két évvel ezelőtt a fertőzött növények aránya 37% volt. Úgy gondoljuk, hogy egy kezelés segített, és tesztelni szeretnénk azt az állítást, hogy csökkent a fertőzött növények aránya.

A formális hipotézis teszt összetevői

A nullhipotézis egy populációs paraméter értékére vonatkozó állítás, például a populáció átlaga (µ) vagy a populáció aránya (p). Tartalmazza az egyenlőség feltételét, és H ₀ (H-Naught) jelöli.

H ₀: µ = 157 vagy H0: p = 0,37

Az alternatív hipotézis a tesztelendő állítás, a nullhipotézis ellentéte. _{Tartalmazza annak a paraméternek az értékét, amelyet hihetőnek tartunk, és amelyet H 1-nek jelölünk.}

H ₁: µ > 157 vagy H1: p ≠ 0,37

A tesztstatisztika a mintaadatokból kiszámított érték, amelyet a nullhipotézis elutasításáról szóló döntés meghozatalához használnak. A tesztstatisztika átalakítja a minta átlagát (x) vagy a minta arányát (p) Z- vagy t-pontszámra azzal a feltételezéssel, hogy a nullhipotézis igaz. Annak eldöntésére használják, hogy a minta statisztikája és a feltételezett állítás közötti különbség szignifikáns-e.

A p-érték a görbe alatti terület a tesztstatisztikától balra vagy jobbra. Összehasonlítják a szignifikancia szintjével (α).

A kritikus érték az az érték, amely meghatározza az elutasítási zónát (a tesztstatisztikai értékek, amelyek a nullhipotézis elutasításához vezetnének). Ezt a szignifikancia szintje határozza meg.

A szignifikancia szintje (α) annak a valószínűsége, hogy a tesztstatisztika a kritikus régióba esik, ha a nullhipotézis igaz. Ezt a szintet a kutató határozza meg.

A következtetés a hipotézis teszt végső döntése. A következtetést mindig egyértelműen meg kell határozni, közölve a döntést a teszt összetevői alapján. Fontos felismerni, hogy soha nem bizonyítjuk vagy fogadjuk el a nullhipotézist. Csupán azt mondjuk, hogy a minta bizonyítéka nem elég erős ahhoz, hogy indokolja a nullhipotézis elutasítását. A következtetés két részből áll:

1) Elutasítja vagy nem utasítja el a nullhipotézist, és 2) van vagy nincs elegendő bizonyíték az alternatív állítás alátámasztására.

1. lehetőség) Elutasítja a nullhipotézist (H0). Ez azt jelenti, hogy elegendő statisztikai bizonyítékkal rendelkezik az alternatív állítás alátámasztására (H ₁).

2. lehetőség) Nem sikerült elutasítani a nullhipotézist (H0). Ez azt jelenti, hogy NEM rendelkezik elegendő bizonyítékkal az alternatív állítás alátámasztására (H ₁).

A hipotézisek tesztelésének másik módja az, ha összehasonlítjuk az amerikai igazságszolgáltatási rendszerrel. A vádlott ártatlan, amíg bűnösségét be nem bizonyítják (Nullhipotézis - ártatlan). Az ügyész megpróbálja bizonyítani, hogy a vádlott bűnös (Alternatív hipotézis - bűnös). Két lehetséges következtetést vonhat le a zsűri. Először is, az alperes bűnös (Elutasítja a nullhipotézist). Másodszor, az alperes nem bűnös (nem utasítja el a nullhipotézist). Ez nem ugyanaz, mint azt mondani, hogy a vádlott ártatlan! Az első esetben az ügyésznek elegendő bizonyítéka volt ahhoz, hogy elutasítsa a nullhipotézist (ártatlan) és támogassa az alternatív állítást (bűnös). A második esetben az ügyésznek NEM volt elegendő bizonyítéka a nullhipotézis elutasításához (ártatlan) és az alternatív bűnösség állításának alátámasztásához.

A null és alternatív hipotézisek

Három különböző null- és alternatív hipotézispár létezik:

Táblázat\(PageIndex{1}\): A kétoldalas hipotézis teszt elutasítási zónája.

Kétoldalas	Baloldali	Jobb oldali
\(\mathrm{H}_{\mathrm{O}}: \boldsymbol{\mu}=\mathrm{c}\)	\(\mathbf{H}_{\mathbf{0}}: \boldsymbol{\mu}=\mathbf{C}\)	\(\mathbf{H}_{\mathbf{0}}: \boldsymbol{\mu}=\mathbf{C}\)
\(\mathbf{H}_{\mathbf{1}}: \boldsymbol{\mu \neq \mathbf { C }}\)	\(\mathbf{H}_{\mathbf{1}}: \boldsymbol{\mu}< \mathbf{C}\)	\(\mathbf{H}_{\mathbf{1}}: \boldsymbol{\mu}>\mathbf{C}\)

ahol c valamilyen ismert érték.

Kétoldalas teszt

Ez azt teszteli, hogy a populációs paraméter egyenlő-e valamilyen konkrét értékkel, szemben azzal, hogy nem egyenlő.

Ho: μ = 12 vs. H ₁: μ ≠ 12

A kritikus régió egyenlően oszlik meg a két farokra, és a kritikus értékek ± értékek, amelyek meghatározzák az elutasítási zónákat.

Mi a clipboard_ecbcf5ea9f153334c86a41f7b1aefc225.png — Ábra\(\PageIndex{1}\): A kétoldalas hipotézis teszt elutasítási zónája.

Példa \(\PageIndex{3}\):

A vörösfenyő átmérőjének növekedését vizsgáló erdész úgy véli, hogy az átlagos átmérőnövekedés eltérő lesz, ha trágyázási kezelést alkalmaznak az állományra.

Ho: μ = 1,2 in./ év
H ₁: μ ≠ 1,2 in./ év

Ez kétoldalú kérdés, mivel az erdész nem mondja ki, hogy a népesség átlagos átmérőjének növekedése növekedni fog vagy csökken.

Jobb oldali teszt

Ez azt teszteli, hogy a populációs paraméter egyenlő-e valamilyen konkrét értékkel, szemben a nagyobb értékkel.

Ho: μ = 12 vs. H ₁: μ > 12

A kritikus régió a jobb farokban van, a kritikus érték pedig egy pozitív érték, amely meghatározza az elutasítási zónát.

Mi a clipboard_efe68d0df0cbc7e840bff49a6ad570d34.png — Ábra\(\PageIndex{2}\): *A jobb oldali hipotézis teszt elutasítási zónája*.

Példa \(\PageIndex{4}\):

Egy biológus úgy véli, hogy az utolsó öt évvel ezelőtti vizsgálat óta nőtt az invazív fajjal fertőzött tavak átlagos száma.

Ho: μ = 15 tavak
H1: μ > 15 tavak

Ez egy jobboldali kérdés, mivel a biológus úgy véli, hogy nőtt a fertőzött tavak népességének átlagos száma.

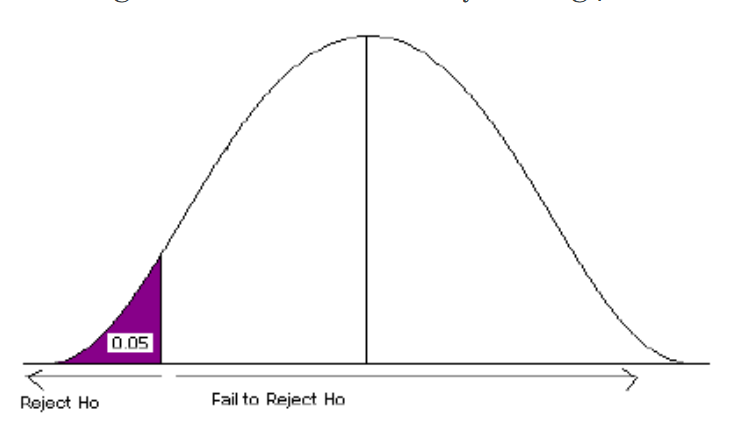
Bal oldali teszt

Ez azt teszteli, hogy a populációs paraméter egyenlő-e valamilyen konkrét értékkel, szemben a kisebb értékkel.

Ho: μ = 12 vs. H ₁: μ < 12

A kritikus régió a bal farokban van, a kritikus érték pedig egy negatív érték, amely meghatározza az elutasítási zónát.

Mi a clipboard_eba848435a52a251915e6261b9a4317e4.png — Ábra\(\PageIndex{3}\): *A baloldali hipotézis teszt elutasítási zónája*.

Példa \(\PageIndex{5}\):

Egy tudós kutatása azt mutatja, hogy megváltozott az egyes környezetvédelmi politikákat támogató emberek aránya. Tesztelni akarja azt az állítást, hogy csökkent az e politikákat támogató emberek aránya.

Ho: p = 0,57
H ₁: p < 0,57

Ez egy baloldali kérdés, mivel a tudós úgy véli, hogy csökkent a valódi népességarány.

Statisztikailag szignifikáns

Ha a megfigyelt eredmények (a minta statisztikái) valószínűtlenek (alacsony valószínűség), feltételezve, hogy a nullhipotézis igaz, azt mondjuk, hogy az eredmény statisztikailag szignifikáns, és elutasítjuk a nullhipotézist. Ez az eredmény a szignifikancia szintjétől, a minta statisztikájától, a minta méretétől és attól függ, hogy ez egy- vagy kétoldalú alternatív hipotézis.

A hibák típusai

A tesztelés során arra a következtetésre jutunk, hogy elutasítjuk a nullhipotézist, vagy nem utasítjuk el a nullhipotézist. Az ilyen következtetések néha helyesek és néha helytelenek (még akkor is, ha minden helyes eljárást követtünk). Hiányos mintaadatokat használunk a következtetés levonásához, és mindig fennáll annak a lehetősége, hogy rossz következtetést vonjunk le. A hipotézisek teszteléséből négy lehetséges következtetést lehet levonni. A négy lehetséges eredmény közül kettő helyes, kettő NEM helyes.

Táblázat\(\PageIndex{2}\). A hipotézis teszt lehetséges eredményei.

	H ₀ igaz	H ₁ igaz
_{Ne utasítsa el a H 0}	Helyes következtetés	II. Típusú hiba
_{H 0 elutasítása}	I. típusú hiba	Helyes következtetés

Az I. típusú hiba az, amikor elutasítjuk a nullhipotézist, amikor igaz. Az α (alfa) szimbólum az I. típusú hibák ábrázolására szolgál. Ez ugyanaz az alfa, amelyet a szignifikancia szintjeként használunk. Azáltal, hogy az alfát a lehető legalacsonyabbra állítjuk, megpróbáljuk az I. típusú hibát a szignifikancia szintjén keresztül irányítani.

A II. Típusú hiba az, amikor nem utasítjuk el a nullhipotézist, ha hamis. A β (béta) szimbólum a II. Típusú hibák ábrázolására szolgál.

Általában az I. típusú hibákat súlyosabbnak tekintik. A hipotézisvizsgálati eljárás egyik lépése magában foglalja a szignifikancia szint kiválasztását (α), amely annak valószínűsége, hogy elutasítják a nullhipotézist, ha helyes. Így a kutató kiválaszthatja azt a szignifikanciaszintet, amely minimalizálja az I. típusú hibákat. Van azonban matematikai kapcsolat α, β és n között (minta mérete).

Ahogy α növekszik, β csökken
Ahogy α csökken, β növekszik
Ahogy a minta mérete növekszik (n), mind α, mind β csökken

A természetes hajlam az α lehető legkisebb értékének kiválasztása, úgy gondolva, hogy minimalizálja az I. típusú hiba okozásának lehetőségét. Sajnos ez a II. Típusú hibák növekedését kényszeríti. Ha az elutasítási zónát túl kicsivé teszi, előfordulhat, hogy nem utasítja el a nullhipotézist, amikor valójában hamis. Általában a legjobb mintaméretet és szignifikanciaszintet választjuk ki, automatikusan beállítva β.

Mi a clipboard_edc556933d0bd0c07e0f046180aae8a6c.png — Ábra\(\PageIndex{4}\): *1. típusú hiba.*

4. ábra.

A teszt ereje

A II. Típusú hiba (β) annak a valószínűsége, hogy nem utasítják el a hamis nullhipotézist. Ebből következik, hogy 1-β a hamis nullhipotézis elutasításának valószínűsége. Ezt a valószínűséget a teszt erejeként azonosítják, és gyakran használják a teszt hatékonyságának felmérésére annak felismerésében, hogy a nullhipotézis hamis.

Meghatározás: a teszt teljesítménye

Annak valószínűségét, hogy rögzített szinten α szignifikancia teszt elutasítja H0, ha a paraméter egy adott alternatív értéke igaz, a teszt erejének nevezzük.

A teljesítmény közvetlenül kapcsolódik a minta méretéhez is. Tegyük fel például, hogy a nullhipotézis az, hogy az átlagos haltömeg 8,7 lb. Tekintettel a mintaadatokra, 5% -os szignifikanciaszintre és 9,2 lb alternatív tömegre, kiszámíthatjuk a teszt erejét μ = 8.7 lb elutasítására. Ha kis mintaméretünk van, a teljesítmény alacsony lesz. A minta méretének növelése azonban növeli a teszt teljesítményét. A jelentőség szintjének növelése szintén növeli a hatalmat. Az 5% -os szignifikanciateszt nagyobb eséllyel utasítja el a nullhipotézist, mint egy 1% -os teszt, mivel az elutasításhoz szükséges bizonyítékok erőssége kisebb. A szórás csökkentésének ugyanaz a hatása, mint a minta méretének növelése: több információ található a μ -ról.