7.2: Mifumo ya Equations Linear - Vigezo viwili
- Page ID
- 180954
- Tatua mifumo ya equations kwa kuchora.
- Tatua mifumo ya equations kwa kubadilisha.
- Tatua mifumo ya equations kwa kuongeza.
- Tambua mifumo isiyoendana ya milinganyo iliyo na vigezo viwili.
- Eleza suluhisho la mfumo wa equations tegemezi iliyo na vigezo viwili.
Mtengenezaji wa skateboard huanzisha mstari mpya wa bodi. Mtengenezaji hufuatilia gharama zake, ambayo ni kiasi kinachotumia kuzalisha bodi, na mapato yake, ambayo ni kiasi kinachopata kupitia mauzo ya bodi zake. Kampuni inawezaje kuamua ikiwa inafanya faida na mstari wake mpya? Ni skateboards ngapi zinapaswa kuzalishwa na kuuzwa kabla ya faida iwezekanavyo? Katika sehemu hii, tutazingatia equations linear na vigezo viwili kujibu maswali haya na sawa.

Utangulizi wa Mifumo ya Equations
Ili kuchunguza hali kama ile ya mtengenezaji wa skateboard, tunahitaji kutambua kwamba tunashughulika na variable zaidi ya moja na uwezekano zaidi ya moja equation. Mfumo wa equations linear ina milinganyo mbili au zaidi linear iliyoundwa na vigezo mbili au zaidi kama vile equations zote katika mfumo ni kuchukuliwa wakati huo huo. Ili kupata suluhisho la kipekee kwa mfumo wa equations linear, tunapaswa kupata thamani ya namba kwa kila variable katika mfumo ambao utakidhi equations zote katika mfumo kwa wakati mmoja. Mifumo mingine ya mstari inaweza kuwa na suluhisho na wengine wanaweza kuwa na idadi isiyo na kipimo cha ufumbuzi. Ili mfumo wa mstari uwe na suluhisho la kipekee, lazima iwe na angalau milinganyo mingi kama kuna vigezo. Hata hivyo, hii haina uhakika wa ufumbuzi wa kipekee.
Katika sehemu hii, tutaangalia mifumo ya equations linear katika vigezo viwili, ambayo inajumuisha equations mbili ambazo zina vigezo viwili tofauti. Kwa mfano, fikiria mfumo wafuatayo wa equations linear katika vigezo viwili.
\[\begin{align*} 2x+y &= 15 \\ 3x–y &= 5 \end{align*}\]
Suluhisho la mfumo wa equations linear katika vigezo viwili ni jozi yoyote iliyoamriwa ambayo inatimiza kila equation kwa kujitegemea. Katika mfano huu, jozi iliyoamriwa\((4,7)\) ni suluhisho la mfumo wa equations linear. Tunaweza kuthibitisha ufumbuzi kwa kubadilisha maadili katika kila equation ili kuona kama jozi kuamuru satisfies equations wote. Muda mfupi tutachunguza njia za kutafuta suluhisho hilo ikiwa lipo.
\[\begin{align*} 2(4)+(7) &=15 \text{ True} \\ 3(4)−(7) &= 5 \text{ True} \end{align*}\]
Mbali na kuzingatia idadi ya equations na vigezo, tunaweza kuainisha mifumo ya equations linear na idadi ya ufumbuzi. Mfumo thabiti wa equations una angalau suluhisho moja. Mfumo thabiti unachukuliwa kuwa mfumo wa kujitegemea ikiwa una suluhisho moja, kama mfano tuliochunguza tu. Mistari miwili ina mteremko tofauti na huingiliana wakati mmoja katika ndege. Mfumo thabiti unachukuliwa kuwa mfumo wa tegemezi ikiwa milinganyo ina mteremko sawa na y -intercepts sawa. Kwa maneno mengine, mistari sanjari hivyo equations kuwakilisha mstari huo. Kila hatua kwenye mstari inawakilisha jozi ya kuratibu ambayo inatimiza mfumo. Hivyo, kuna idadi isiyo na kipimo ya ufumbuzi.
Aina nyingine ya mfumo wa equations linear ni mfumo usioendana, ambayo ni moja ambayo equations inawakilisha mistari miwili sambamba. Mstari una mteremko sawa na tofauti y- intercepts. Hakuna pointi za kawaida kwa mistari yote; kwa hiyo, hakuna suluhisho kwa mfumo.
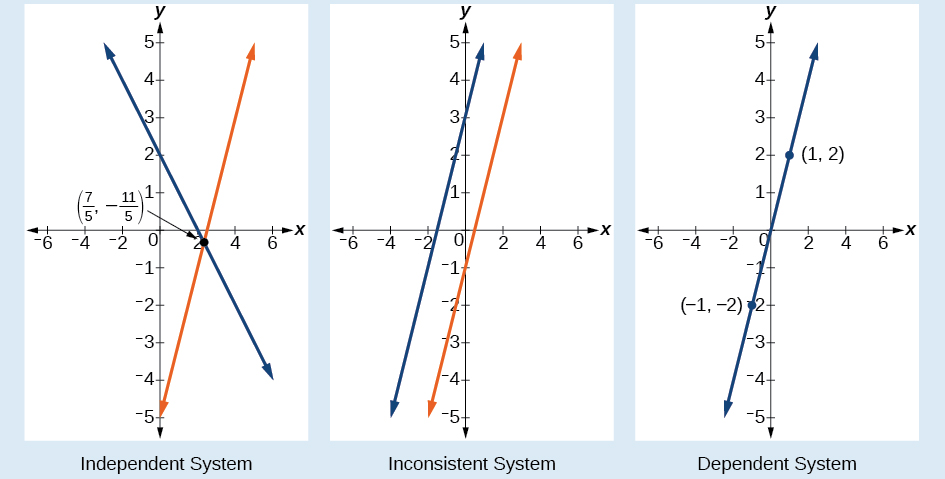
Kuna aina tatu za mifumo ya equations linear katika vigezo viwili, na aina tatu za ufumbuzi.
- Mfumo wa kujitegemea una jozi moja ya suluhisho\((x,y)\). Hatua ambapo mistari miwili inakabiliana ni suluhisho pekee.
- Mfumo usioendana hauna suluhisho. Kumbuka kwamba mistari miwili ni sambamba na kamwe intersect.
- Mfumo wa tegemezi una ufumbuzi mkubwa sana. Mstari huo ni sawa. Wao ni mstari huo, hivyo kila jozi ya kuratibu kwenye mstari ni suluhisho la equations zote mbili.
Kielelezo\(\PageIndex{2}\) kulinganisha uwakilishi graphical ya kila aina ya mfumo.
- Badilisha jozi iliyoamuru katika kila equation katika mfumo.
- Kuamua kama kauli za kweli zinatokana na uingizwaji katika equations zote mbili; ikiwa ndivyo, jozi iliyoamriwa ni suluhisho.
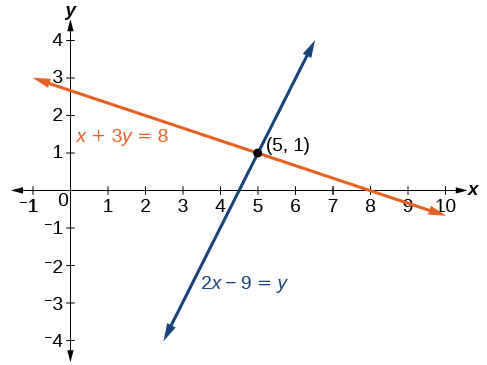
Kuamua kama jozi iliyoamriwa\((5,1)\) ni suluhisho la mfumo uliopewa wa equations.
\[\begin{align*} x+3y &= 8 \\ 2x−9 &= y \end{align*}\]
Suluhisho
Badilisha jozi iliyoamriwa\((5,1)\) katika equations zote mbili.
\[ \begin{align*} (5)+3(1) &= 8 \\ 8 &= 8 \text{ True} \\ 2(5)−9 &= (1) \\ 1 &= 1 \text{ True} \end{align*}\]
Jozi iliyoamriwa\((5,1)\) inatimiza equations zote mbili, hivyo ni suluhisho la mfumo.
Uchambuzi
Tunaweza kuona suluhisho wazi kwa kupanga mipango ya kila equation. Kwa kuwa suluhisho ni jozi iliyoamriwa ambayo inatimiza equations zote mbili, ni hatua kwenye mistari yote na hivyo hatua ya makutano ya mistari miwili. Angalia Kielelezo\(\PageIndex{3}\).
Kuamua kama jozi iliyoamriwa\((8,5)\) ni suluhisho la mfumo wafuatayo.
\[\begin{align*} 5x−4y &= 20 \\ 2x+1 &= 3y \end{align*}\]
- Jibu
-
Sio suluhisho.
Kutatua Mifumo ya Equations kwa Graphing
Kuna njia nyingi za kutatua mifumo ya equations linear. Kwa mfumo wa equations linear katika vigezo viwili, tunaweza kuamua aina zote za mfumo na suluhisho kwa kuchora mfumo wa equations kwenye seti sawa ya axes.
Tatua mfumo wafuatayo wa equations kwa kuchora. Tambua aina ya mfumo.
\[\begin{align*} 2x+y &= −8 \\ x−y &= −1 \end{align*}\]
Suluhisho
Kutatua equation kwanza kwa\(y\).
\[\begin{align*} 2x+y &= −8 \\ y &= −2x−8 \end{align*}\]
Kutatua equation pili kwa\(y\).
\[\begin{align*} x−y &= −1 \\ y &= x+1 \end{align*}\]
Grafu equations wote juu ya seti sawa ya axes kama katika Kielelezo\(\PageIndex{4}\).
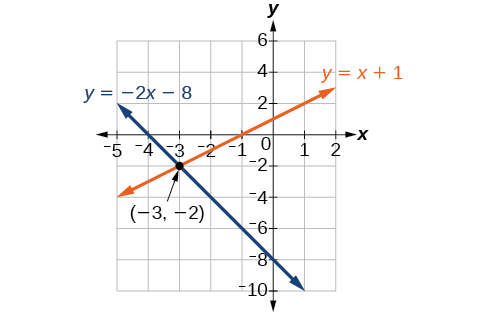
Mstari huonekana kuingiliana wakati huo\((−3,−2)\). Tunaweza kuangalia ili kuhakikisha kwamba hii ni suluhisho la mfumo kwa kubadili jozi iliyoamriwa katika equations zote mbili.
\[\begin{align*} 2(−3)+(−2) &= −8 \\ −8 &= −8 \text{ True} \\ (−3)−(−2) &= −1 \\ −1 &= −1 \text{ True} \end{align*}\]
Suluhisho la mfumo ni jozi iliyoamriwa\((−3,−2)\), hivyo mfumo ni huru.
Tatua mfumo wafuatayo wa equations kwa kuchora.
\[\begin{align*} 2x−5y &= −25 \\ −4x+5y &= 35 \end{align*}\]
- Jibu
-
Suluhisho la mfumo ni jozi iliyoamriwa\((−5,3)\).
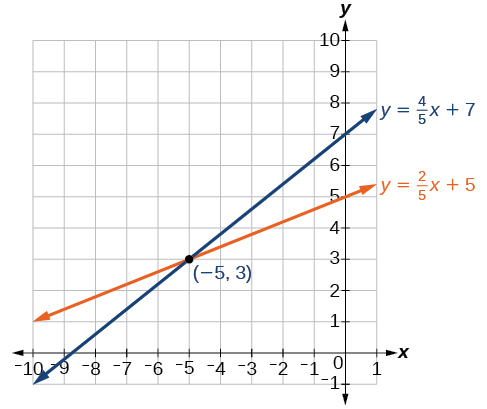
Kielelezo\(\PageIndex{5}\)
Je, graphing inaweza kutumika kama mfumo ni haiendani au tegemezi?
Ndiyo, katika kesi zote mbili tunaweza bado grafu mfumo kuamua aina ya mfumo na ufumbuzi. Ikiwa mistari miwili ni sambamba, mfumo hauna suluhisho na haukubaliani. Ikiwa mistari miwili inafanana, mfumo una ufumbuzi usio na mwisho na ni mfumo wa tegemezi.
Kutatua Mifumo ya Equations kwa Kubadilisha
Kutatua mfumo wa mstari katika vigezo viwili kwa kuchora kazi vizuri wakati suluhisho lina maadili ya integer, lakini ikiwa suluhisho letu lina decimals au sehemu ndogo, sio njia sahihi zaidi. Tutazingatia njia mbili zaidi za kutatua mfumo wa equations linear ambayo ni sahihi zaidi kuliko graphing. Njia moja ni kutatua mfumo wa equations kwa njia ya kubadilisha, ambayo sisi kutatua moja ya equations kwa variable moja na kisha kubadilisha matokeo katika equation ya pili kutatua kwa variable pili. Kumbuka kwamba tunaweza kutatua kwa kutofautiana moja tu kwa wakati, ambayo ndiyo sababu njia ya kubadilisha ni ya thamani na ya vitendo.
- Kutatua moja ya equations mbili kwa moja ya vigezo katika suala la nyingine.
- Badilisha maneno ya kutofautiana hii katika equation ya pili, kisha kutatua kwa kutofautiana iliyobaki.
- Mbadala kwamba ufumbuzi katika mojawapo ya milinganyo ya awali ili kupata thamani ya kutofautiana kwanza. Ikiwezekana, weka suluhisho kama jozi iliyoamriwa.
- Angalia suluhisho katika equations zote mbili.
Tatua mfumo wafuatayo wa equations kwa kubadilisha.
\[\begin{align*} −x+y &= −5 \\ 2x−5y &= 1 \end{align*}\]
Suluhisho
Kwanza, sisi kutatua equation kwanza kwa\(y\).
\[\begin{align*} −x+y &=−5 \\ y &= x−5 \end{align*}\]
Sasa tunaweza mbadala ya kujieleza\(x−5\) kwa\(y\) katika equation ya pili.
\[\begin{align*} 2x−5y &= 1 \\ 2x−5(x−5) &= 1 \\ 2x−5x+25 &= 1 \\ −3x &= −24 \\ x &= 8 \end{align*}\]
Sasa, sisi badala\(x=8\) katika equation kwanza na kutatua kwa\(y\).
\[\begin{align*} −(8)+y &= −5 \\ y &= 3 \end{align*}\]
Suluhisho letu ni\((8,3)\).
Angalia suluhisho kwa kubadili\((8,3)\) katika equations zote mbili.
\[\begin{align*} −x+y &= −5 \\ −(8)+(3) &= −5 \text{ True} \\ 2x−5y &= 1 \\ 2(8)−5(3) &= 1 \text{ True} \end{align*}\]
Tatua mfumo wafuatayo wa equations kwa kubadilisha.
\[\begin{align*} x &= y+3 \\ 4 &= 3x−2y \end{align*}\]
- Jibu
-
\((−2,−5)\)
Je, njia ya kubadilisha inaweza kutumika kutatua mfumo wowote wa mstari katika vigezo viwili?
Ndiyo, lakini njia hiyo inafanya kazi bora ikiwa moja ya equations ina mgawo wa\(1\) au\(–1\) hivyo kwamba hatuhitaji kukabiliana na sehemu ndogo.
Kutatua Mifumo ya Equations katika Vigezo viwili kwa Njia ya Kuongeza
Njia ya tatu ya kutatua mifumo ya equations linear ni njia ya kuongeza. Kwa njia hii, tunaongeza maneno mawili na kutofautiana sawa, lakini coefficients kinyume, ili jumla ni sifuri. Bila shaka, si mifumo yote iliyoanzishwa na masharti mawili ya kutofautiana moja kuwa na coefficients kinyume. Mara nyingi tunapaswa kurekebisha moja au yote ya equations kwa kuzidisha ili kutofautiana moja itaondolewa kwa kuongeza.
- Andika equations zote mbili na x - na y -vigezo upande wa kushoto wa ishara sawa na mara kwa mara upande wa kulia.
- Andika equation moja juu ya nyingine, bitana up vigezo sambamba. Ikiwa moja ya vigezo katika equation ya juu ina mgawo tofauti wa kutofautiana sawa katika equation ya chini, ongeza equations pamoja, kuondoa variable moja. Ikiwa sio, tumia kuzidisha kwa nambari isiyo ya zero ili moja ya vigezo katika equation ya juu ina mgawo wa kinyume wa kutofautiana sawa katika equation ya chini, kisha kuongeza equations kuondokana na kutofautiana.
- Kutatua equation kusababisha kwa variable iliyobaki.
- Mbadala kwamba thamani katika moja ya milinganyo ya awali na kutatua kwa variable pili.
- Angalia suluhisho kwa kubadili maadili katika equation nyingine.
Tatua mfumo uliotolewa wa equations kwa kuongeza.
\[\begin{align*} x+2y &= −1 \\ −x+y &=3 \end{align*}\]
Suluhisho
Equations zote mbili tayari zimewekwa sawa na mara kwa mara. Kumbuka kwamba mgawo wa\(x\) katika equation ya pili\(–1\),, ni kinyume cha mgawo wa\(x\) katika equation kwanza,\(1\). Tunaweza kuongeza equations mbili kuondokana\(x\) bila wanaohitaji kuzidisha kwa mara kwa mara.
\[\begin{align*} x+2y &= -1 \\ \underline{-x+y}& = \underline{3} \\ 3y&= 2 \\ \end{align*}\]
Sasa kwa kuwa tuna kuondolewa\(x\), tunaweza kutatua equation kusababisha kwa\(y\).
\[\begin{align*} 3y &= 2 \\ y &=\dfrac{2}{3} \end{align*}\]
Kisha, sisi badala ya thamani hii kwa\(y\) moja ya equations awali na kutatua kwa\(x\).
\[\begin{align*} −x+y &= 3 \\ −x+\dfrac{2}{3} &= 3 \\ −x &= 3−\dfrac{2}{3} \\ −x &= \dfrac{7}{3} \\ x &= −\dfrac{7}{3} \end{align*}\]
Suluhisho la mfumo huu ni\(\left(−\dfrac{7}{3},\dfrac{2}{3}\right)\).
Angalia suluhisho katika equation ya kwanza.
\[\begin{align*} x+2y &= −1 \\ \left(−\dfrac{7}{3}\right)+2\left(\dfrac{2}{3}\right) &= \\ −\dfrac{7}{3}+\dfrac{4}{3} &= −\dfrac{3}{3} \\ −1 &= −1 \;\;\;\;\;\;\;\; \text{True} \end{align*}\]
Uchambuzi
Tunapata mtazamo muhimu juu ya mifumo ya equations kwa kuangalia uwakilishi wa graphical. Angalia Kielelezo\(\PageIndex{6}\) ili kupata kwamba equations intersect katika ufumbuzi. Hatuna haja ya kuuliza kama kunaweza kuwa na suluhisho la pili kwa sababu kuchunguza grafu inathibitisha kwamba mfumo una suluhisho moja hasa.
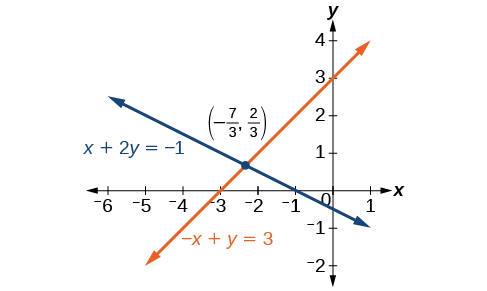
Tatua mfumo uliotolewa wa equations kwa njia ya kuongeza.
\[\begin{align*} 3x+5y &= −11 \\ x−2y &= 11 \end{align*}\]
Suluhisho
Kuongeza milinganyo haya kama ilivyowasilishwa haitaondoa kutofautiana. Hata hivyo, tunaona kwamba equation ya kwanza ina\(3x\) ndani yake na equation ya pili ina\(x\). Hivyo kama sisi kuzidisha equation pili na\(−3\), x - suala kuongeza sifuri.
\[\begin{align*} x−2y &= 11 \\ −3(x−2y) &=−3(11) \;\;\;\;\;\;\;\; \text{Multiply both sides by }−3. \\ −3x+6y &= −33 \;\;\;\;\;\;\;\;\; \text{Use the distributive property.} \end{align*}\]
Sasa, hebu tuwaongeze.
\[\begin{align*} 3x+5y &= -11 \\ \underline{-3x+6y }& = \underline{-33} \\ 11y&= -44 \\ y&= -4 \end{align*}\]
Kwa hatua ya mwisho, sisi badala ya\(y=−4\) moja ya equations awali na kutatua kwa\(x\).
\[\begin{align*} 3x+5y &= −11 \\ 3x+5(−4) &= −11 \\ 3x−20 &= −11 \\ 3x &= 9 \\ x &= 3 \end{align*}\]
Suluhisho letu ni jozi iliyoamriwa\((3,−4)\). Angalia Kielelezo\(\PageIndex{7}\). Angalia suluhisho katika equation ya awali ya pili.
\[\begin{align*} x−2y &= 11 \\ (3)−2(−4) &= 3+8 \\ &= 11 \;\;\;\;\;\;\;\;\;\; \text{True} \end{align*}\]
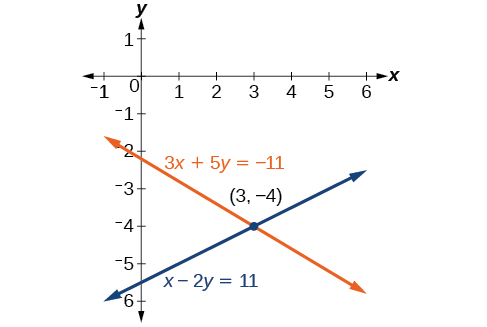
Tatua mfumo wa equations kwa kuongeza.
\[\begin{align*} 2x−7y &= 2 \\ 3x+y &= −20 \end{align*}\]
- Jibu
-
\((−6,−2)\)
Tatua mfumo uliotolewa wa equations katika vigezo viwili kwa kuongeza.
\[\begin{align*} 2x+3y &= −16 \\ 5x−10y &= 30 \end{align*}\]
Suluhisho
Equation moja ina\(2x\) na nyingine ina\(5x\). Nyingi ya kawaida ni\(10x\) hivyo tutalazimika kuzidisha equations zote mbili kwa mara ili kuondokana na variable moja. Hebu kuondokana\(x\) na kuzidisha equation kwanza na\(−5\) na equation pili na\(2\).
\[\begin{align*} −5(2x+3y) &= −5(−16) \\ −10x−15y &= 80 \\ 2(5x−10y) &= 2(30) \\ 10x−20y &= 60 \end{align*}\]
Kisha, tunaongeza equations mbili pamoja.
\[\begin{align*} -10x-15y &= 80 \\ \underline{10x-20y}& = \underline{60} \\ -35y&= 140 \\ y&= -4 \end{align*}\]
Mbadala\(y=−4\) katika equation ya awali ya kwanza.
\[ \begin{align*} 2x+3(−4) &=−16 \\ 2x−12 &= −16 \\ 2x &= −4 \\ x &=−2 \end{align*}\]
Suluhisho ni\((−2,−4)\). Angalia katika equation nyingine.
\[\begin{align*} 5x−10y &= 30 \\ 5(−2)−10(−4) &= 30 \\ −10+40 &= 30 \\30 &=30 \end{align*}\]
Angalia Kielelezo\(\PageIndex{8}\).
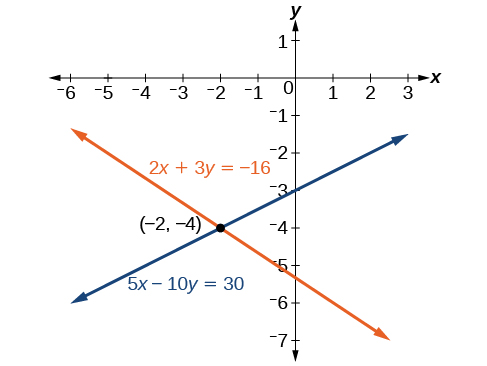
Tatua mfumo uliotolewa wa equations katika vigezo viwili kwa kuongeza.
\[ \begin{align*} \dfrac{x}{3}+\dfrac{y}{6} &= 3 \\ \dfrac{x}{2}−\dfrac{y}{4} &= 1 \end{align*}\]
Suluhisho
Kwanza wazi kila equation ya sehemu kwa kuzidisha pande zote mbili za equation na denominator angalau kawaida.
\[\begin{align*} 6\left(\dfrac{x}{3}+\dfrac{y}{6}\right) &= 6(3) \\ 2x+y &= 18 \\ 4\left(\dfrac{x}{2}−\dfrac{y}{4}\right) &= 4(1) \\ 2x−y &= 4 \end{align*}\]
Sasa kuzidisha equation pili kwa\(−1\) ili tuweze kuondoa x -variable.
\[\begin{align*} −1(2x−y) &= −1(4) \\ −2x+y &= −4 \end{align*}\]
Kuongeza equations mbili kuondokana\(x\) -variable na kutatua equation kusababisha.
\[\begin{align*} 2x+y &= 18 \\ −2x+y &= −4 \\ 2y &= 14 \\ y &=7 \end{align*}\]
Mbadala\(y=7\) katika equation kwanza.
\[\begin{align*} 2x+(7) &= 18 \\ 2x &= 11 \\ x &= \dfrac{11}{2} \\ &= 7.5 \end{align*}\]
Suluhisho ni\(\left(\dfrac{11}{2},7\right)\). Angalia katika equation nyingine.
\[\begin{align*} \dfrac{x}{2}−\dfrac{y}{4} &= 1 \\ \dfrac{\dfrac{11}{2}}{2}−\dfrac{7}{4} &=1 \\ \dfrac{11}{4}−\dfrac{7}{4} &=1 \\ \dfrac{4}{4} &=1 \end{align*}\]
Tatua mfumo wa equations kwa kuongeza.
\[\begin{align*} 2x+3y &= 8 \\ 3x+5y &= 10 \end{align*}\]
- Jibu
-
\((10,−4)\)
Kutambua Mifumo isiyoendana ya milinganyo iliyo na vigezo viwili
Sasa kwa kuwa tuna mbinu kadhaa za kutatua mifumo ya equations, tunaweza kutumia mbinu kutambua mifumo isiyoendana. Kumbuka kwamba mfumo usioendana una mistari sambamba ambayo ina mteremko huo lakini tofauti y-intercepts. Wao kamwe intersect. Wakati wa kutafuta suluhisho la mfumo usioendana, tutakuja na taarifa ya uongo, kama vile\(12=0\).
Tatua mfumo wafuatayo wa equations.
\[\begin{align*} x &= 9−2y \\ x+2y &= 13 \end{align*}\]
Suluhisho
Tunaweza kukabiliana na tatizo hili kwa njia mbili. Kwa sababu equation moja tayari kutatuliwa kwa\(x\), hatua dhahiri zaidi ni kutumia badala.
\[\begin{align*} x+2y &= 13 \\ (9−2y)+2y &= 13 \\ 9+0y &= 13 \\ 9 &= 13 \end{align*}\]
Kwa wazi, kauli hii ni utata kwa sababu\(9≠13\). Kwa hiyo, mfumo hauna suluhisho.
Njia ya pili itakuwa ya kwanza kuendesha milinganyo ili wawe wote wawili katika fomu ya mteremko. Sisi kuendesha equation kwanza kama ifuatavyo.
\[\begin{align*} x &= 9−2y \\ 2y &= −x+9 \\ y &= −\dfrac{1}{2}x+\dfrac{9}{2} \end{align*}\]
Sisi kisha kubadilisha equation pili walionyesha kwa mteremka-intercept fomu.
\[\begin{align*} x+2y &= 13 \\ 2y &= −x+13 \\ y &= −\dfrac{1}{2}x+\dfrac{13}{2} \end{align*}\]
Kulinganisha equations, tunaona kwamba wana mteremko huo lakini tofauti\(y\) -intercepts. Kwa hiyo, mistari ni sawa na haipatikani.
\[\begin{align*} y &= −\dfrac{1}{2}x+\dfrac{9}{2} \\ y &= −\dfrac{1}{2}x+\dfrac{13}{2} \end{align*}\]
Uchambuzi
Kuandika equations katika mteremko intercept fomu unathibitisha kwamba mfumo ni haiendani kwa sababu mistari yote intersect hatimaye isipokuwa ni sambamba. Mstari sambamba kamwe intersect; hivyo, mistari miwili haina pointi sawa. Grafu za equations katika mfano huu zinaonyeshwa kwenye Kielelezo\(\PageIndex{9}\).
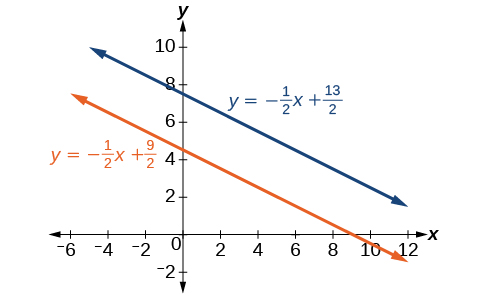
Tatua mfumo wafuatayo wa equations katika vigezo viwili.
\[\begin{align*} 2y−2x &= 2 \\ 2y−2x &= 6 \end{align*}\]
- Jibu
-
Hakuna ufumbuzi. Ni mfumo usioendana.
Kuelezea Suluhisho la Mfumo wa Ulinganisho wa Tegemezi Ukiwa na Vigezo viwili
Kumbuka kwamba mfumo wa tegemezi wa equations katika vigezo viwili ni mfumo ambao equations mbili zinawakilisha mstari huo. Mifumo ya tegemezi ina idadi isiyo na kipimo cha ufumbuzi kwa sababu pointi zote kwenye mstari mmoja pia ni kwenye mstari mwingine. Baada ya kutumia badala au kuongeza, equation kusababisha itakuwa utambulisho, kama vile\(0=0\).
Pata suluhisho la mfumo wa equations kwa kutumia njia ya kuongeza.
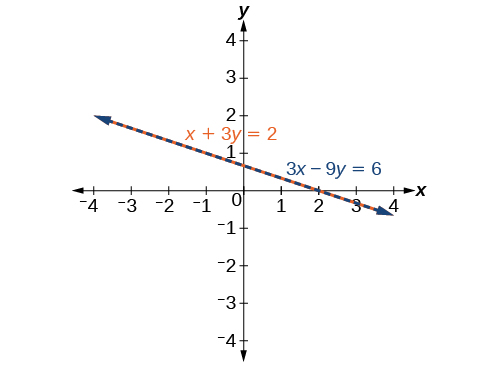
\[\begin{align*} x+3y &= 2 \\ 3x+9y &= 6 \end{align*}\]
Suluhisho
Kwa njia ya kuongeza, tunataka kuondoa moja ya vigezo kwa kuongeza equations. Katika kesi hii, hebu tuzingalie kuondoa\(x\). Kama sisi kuzidisha pande zote mbili za equation kwanza na\(−3\), basi tutakuwa na uwezo wa kuondoa x-variable.
\[\begin{align*} x+3y &= 2 \\ (−3)(x+3y) &= (−3)(2) \\ −3x−9y &= −6 \end{align*}\]
Sasa ongeza equations.
\[\begin{align*} -3x-9y &= -6 \\ \underline{+\space 3x+9y}& = \underline{6} \\ 0&= 0 \\ \end{align*}\]
Tunaweza kuona kwamba kutakuwa na idadi isiyo na kipimo ya ufumbuzi ambayo inakidhi equations zote mbili.
Uchambuzi
Kama sisi rewrote equations wote katika fomu mteremka-intercept, tunaweza kujua nini ufumbuzi bila kuangalia kama kabla ya kuongeza. Hebu tuangalie kile kinachotokea tunapobadilisha mfumo kwa fomu ya kuingilia mteremko.
\[ \begin{align*} x+3y &= 2 \\ 3y &= −x+2 \\ y &= −\dfrac{1}{3}x+\dfrac{2}{3} \\ 3x+9y &= 6 \\ 9y &=−3x+6 \\ y &= −\dfrac{3}{9}x+\dfrac{6}{9} \\ y &= −\dfrac{1}{3}x+\dfrac{2}{3} \end{align*}\]
Angalia Kielelezo\(\PageIndex{10}\). Angalia matokeo ni sawa. Suluhisho la jumla la mfumo ni\(\left(x, −\dfrac{1}{3}x+\dfrac{2}{3}\right)\).
Tatua mfumo wafuatayo wa equations katika vigezo viwili.
\[\begin{align*} y−2x &= 5 \\ −3y+6x &= −15 \end{align*}\]
- Jibu
-
Mfumo unategemea hivyo kuna ufumbuzi usio na kipimo wa fomu\((x,2x+5)\).
Kutumia Mifumo ya Equations Kuchunguza Faida
Kutumia kile tulichojifunza kuhusu mifumo ya equations, tunaweza kurudi tatizo la utengenezaji wa skateboard mwanzoni mwa sehemu hiyo. Kazi ya mapato ya mtengenezaji wa skateboard ni kazi inayotumiwa kuhesabu kiasi cha fedha kinachokuja katika biashara. Inaweza kuwakilishwa na equation\(R=xp\), ambapo\(x\) =wingi na\(p\) =bei. Kazi ya mapato inavyoonekana katika machungwa kwenye Kielelezo\(\PageIndex{11}\).
Kazi ya gharama ni kazi inayotumiwa kuhesabu gharama za kufanya biashara. Inajumuisha gharama za kudumu, kama vile kodi na mishahara, na gharama za kutofautiana, kama vile huduma. Kazi ya gharama inavyoonyeshwa kwa bluu kwenye Kielelezo\(\PageIndex{11}\). \(x\)Axis inawakilisha wingi katika mamia ya vitengo. \(y\)-axis inawakilisha ama gharama au mapato katika mamia ya dola.
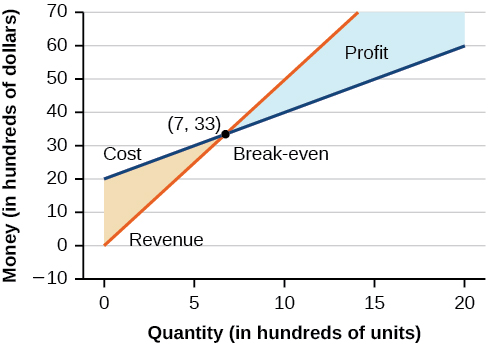
Hatua ambayo mistari miwili inakabiliana inaitwa hatua ya kuvunja hata. Tunaweza kuona kutoka grafu kwamba kama\(700\) vitengo ni zinazozalishwa, gharama ni\($3,300\) na mapato pia\($3,300\). Kwa maneno mengine, kampuni huvunja hata kama huzalisha na kuuza\(700\) vitengo. Hawana pesa wala kupoteza fedha.
Eneo la kivuli kwa haki ya hatua ya kuvunja hata inawakilisha kiasi ambacho kampuni hufanya faida. Eneo la kivuli upande wa kushoto linawakilisha kiasi ambacho kampuni inakabiliwa na hasara. Kazi ya faida ni kazi ya mapato bala kazi ya gharama, imeandikwa kama\(P(x)=R(x)−C(x)\). Kwa wazi, kujua kiasi ambacho gharama ni sawa na mapato ni muhimu sana kwa biashara.
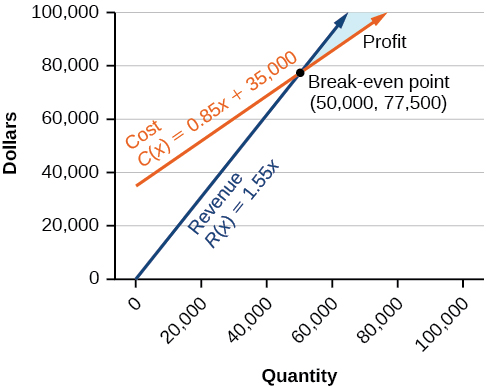
Kutokana\(C(x)=0.85x+35,000\) na kazi ya gharama na kazi ya mapato\(R(x)=1.55x\), pata hatua ya kuvunja hata na kazi ya faida.
Suluhisho
Andika mfumo wa equations\(y\) kutumia nafasi ya kazi notation.
\[\begin{align*} y &= 0.85x+35,000 \\ y &= 1.55x \end{align*}\]
Badala ya kujieleza\(0.85x+35,000\) kutoka equation kwanza katika equation pili na kutatua kwa\(x\).
\[\begin{align*} 0.85x+35,000 &= 1.55x \\ 35,000 &= 0.7x \\ 50,000 &= x \end{align*}\]
Kisha, sisi badala\(x=50,000\) katika ama kazi ya gharama au kazi ya mapato.
\(1.55(50,000)=77,500\)
Hatua ya kuvunja-hata ni\((50,000,77,500)\).
Kazi ya faida inapatikana kwa kutumia formula\(P(x)=R(x)−C(x)\).
\[\begin{align*} P(x) &= 1.55x−(0.85x+35,000) \\ &=0.7x−35,000 \end{align*}\]
Kazi ya faida ni\(P(x)=0.7x−35,000\).
Uchambuzi
Gharama ya kuzalisha\(50,000\) vitengo ni\($77,500\), na mapato kutokana na mauzo ya\(50,000\) vitengo pia\($77,500\). Ili kupata faida, biashara inapaswa kuzalisha na kuuza zaidi ya\(50,000\) vitengo. Angalia Kielelezo\(\PageIndex{12}\).
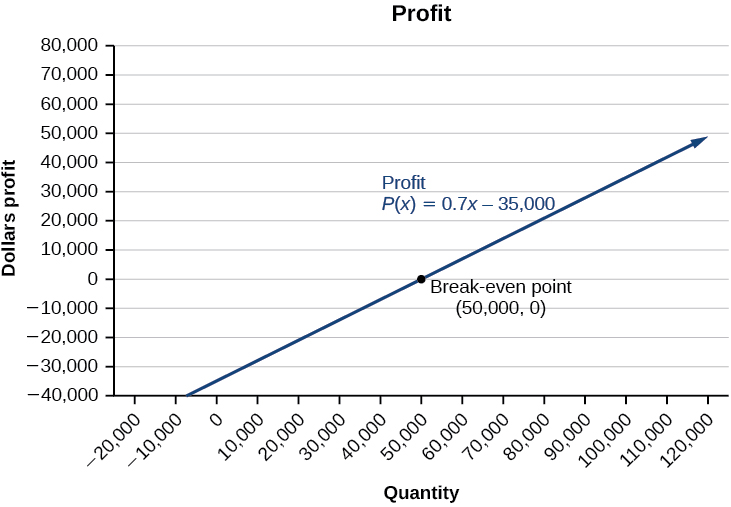
Tunaona kutoka kwenye grafu kwenye Kielelezo\(\PageIndex{13}\) kwamba kazi ya faida ina thamani hasi mpaka\(x=50,000\), wakati grafu inavuka\(x\) -axis. Kisha, grafu inajitokeza kuwa\(y\) maadili mazuri na inaendelea kwenye njia hii kama kazi ya faida ni mstari wa moja kwa moja. Hii inaonyesha kwamba kuvunja-hata uhakika kwa ajili ya biashara hutokea wakati kazi faida ni\(0\). Eneo upande wa kushoto wa hatua ya kuvunja hata inawakilisha kazi kwa hasara.
Gharama ya tiketi ya circus ni\($25.00\) kwa watoto na\($50.00\) kwa watu wazima. Siku fulani, mahudhurio kwenye circus ni\(2,000\) na jumla ya mapato ya lango ni\($70,000\). Ni watoto wangapi na watu wangapi walinunua tiketi?
Suluhisho
Hebu\(c\) = idadi ya watoto na\(a\) = idadi ya watu wazima wanaohudhuria.
Idadi ya watu ni\(2,000\). Tunaweza kutumia hii kuandika equation kwa idadi ya watu katika sarakasi siku hiyo.
\(c+a=2,000\)
Mapato kutoka kwa watoto wote yanaweza kupatikana kwa kuzidisha\($25.00\) kwa idadi ya watoto,\(25c\). Mapato kutoka kwa watu wazima wote yanaweza kupatikana kwa kuzidisha\($50.00\) kwa idadi ya watu wazima,\(50a\). Jumla ya mapato ni\($70,000\). Tunaweza kutumia hii kuandika equation kwa mapato.
\(25c+50a=70,000\)
Sasa tuna mfumo wa equations linear katika vigezo mbili.
\(c+a=2,000\)
\(25c+50a=70,000\)
Katika equation ya kwanza, mgawo wa vigezo vyote ni\(1\). Tunaweza haraka kutatua equation kwanza kwa ama\(c\) au\(a\). Sisi kutatua kwa\(a\).
\[\begin{align*} c+a &= 2,000 \\ a &= 2,000−c \end{align*}\]
Mbadala kujieleza\(2,000−c\) katika equation pili kwa a na kutatua kwa\(c\).
\[\begin{align*} 25c+50(2,000−c) &= 70,000 \\ 25c+100,000−50c &= 70,000 \\ −25c &= −30,000 \\ c &= 1,200 \end{align*}\]
Mbadala\(c=1,200\) katika equation kwanza kutatua kwa\(a\).
\[\begin{align*} 1,200+a &= 2,000 \\ a &= 800 \end{align*}\]
Tunaona kwamba\(1,200\) watoto na\(800\) watu wazima walinunua tiketi kwenye circus siku hiyo.
Tiketi ya chakula kwenye gharama ya circus\($4.00\) kwa watoto na\($12.00\) kwa watu wazima. Ikiwa tiketi za\(1,650\) chakula zilinunuliwa kwa jumla ya,\($14,200\), ni watoto wangapi na watu wazima wangapi walinunua tiketi za chakula?
- Jibu
-
\(700\)watoto,\(950\) watu wazima
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na mifumo ya usawa wa mstari.
Dhana muhimu
- Mfumo wa milinganyo ya mstari una milinganyo miwili au zaidi yenye vigezo viwili au zaidi kama vile equations zote katika mfumo zinachukuliwa wakati huo huo.
- Suluhisho la mfumo wa equations linear katika vigezo viwili ni jozi yoyote iliyoamriwa ambayo inatimiza kila equation kwa kujitegemea. Angalia Mfano\(\PageIndex{1}\).
- Mifumo ya equations huwekwa kama huru na suluhisho moja, inategemea idadi isiyo na kipimo cha ufumbuzi, au haiendani na suluhisho lolote.
- Njia moja ya kutatua mfumo wa equations linear katika vigezo viwili ni kwa graphing. Kwa njia hii, sisi grafu equations juu ya seti moja ya axes. Angalia Mfano\(\PageIndex{2}\).
- Njia nyingine ya kutatua mfumo wa equations linear ni kwa kubadilisha. Kwa njia hii, sisi kutatua kwa variable moja katika equation moja na badala ya matokeo katika equation ya pili. Angalia Mfano\(\PageIndex{3}\).
- Njia ya tatu ya kutatua mfumo wa equations linear ni kwa kuongeza, ambayo tunaweza kuondoa variable kwa kuongeza coefficients kinyume ya vigezo sambamba. Angalia Mfano\(\PageIndex{4}\).
- Mara nyingi ni muhimu kuzidisha equations moja au mbili kwa mara ili kuwezesha kuondoa variable wakati wa kuongeza equations mbili pamoja. Angalia Mfano\(\PageIndex{5}\), Mfano\(\PageIndex{6}\), na Mfano\(\PageIndex{7}\).
- Aidha njia ya kutatua mfumo wa equations matokeo katika taarifa ya uongo kwa mifumo haiendani kwa sababu wao ni alifanya juu ya mistari sambamba kwamba kamwe intersect. Angalia Mfano\(\PageIndex{8}\).
- Suluhisho la mfumo wa equations tegemezi daima kuwa kweli kwa sababu equations zote mbili zinaelezea mstari huo. Angalia Mfano\(\PageIndex{9}\).
- Mifumo ya equations inaweza kutumika kutatua matatizo halisi ya dunia ambayo yanahusisha variable zaidi ya moja, kama vile yale yanayohusiana na mapato, gharama, na faida. Angalia Mfano\(\PageIndex{10}\) na Mfano\(\PageIndex{11}\).


