1.6: Factoring Polynomials

Last updated
Save as PDF

Page ID: 180816

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Katika sehemu hii wanafunzi:

Sababu ni sababu kubwa ya kawaida ya polynomial.
Sababu ya trinomial.
Sababu kwa kikundi.
Factor kamili mraba trinomial.
Sababu tofauti ya mraba.
Fanya jumla na tofauti ya cubes.
Maneno ya sababu kwa kutumia vielelezo vya sehemu au hasi.

Fikiria kwamba tunajaribu kupata eneo la lawn ili tuweze kuamua ni kiasi gani cha mbegu za majani kununua. Lawn ni sehemu ya kijani katika Kielelezo\(\PageIndex{1}\).

Mstatili mkubwa na viwanja vidogo na mstatili ndani. Urefu wa mstatili wa nje ni 6x na upana ni 10x. Urefu wa mraba ni 4 na urefu wa upana wa mstatili wa ndani ni 4. — Kielelezo\(\PageIndex{1}\)

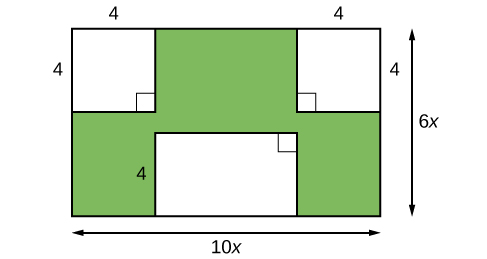
Eneo la mkoa mzima linaweza kupatikana kwa kutumia formula kwa eneo la mstatili.

\[\begin{align*} A &= lw\\ &= 10x\times6x\\ &= 60x^2\; units^2 \end{align*}\]

Sehemu za sehemu ambazo hazihitaji mbegu za nyasi zinahitaji kuondolewa kutoka eneo la kanda nzima. Mikoa miwili ya mraba kila mmoja ina eneo la\(A =s^2=4^2= 16\; units^2\). Mkoa mwingine wa mstatili una upande mmoja wa urefu\(10x−8\) na upande mmoja wa urefu\(4\), kutoa eneo la

\[A =lw=4(10x−8)=40x−32\; \text{units}^2. \nonumber\]

Hivyo kanda ambayo lazima subtracted ina eneo la

\[2(16)+40x−32= 40x\; \text{units}^2. \nonumber\]

Eneo la kanda linalohitaji mbegu za nyasi hupatikana kwa kuondoa\(60x^2−40x\; \text{units}^2\). Eneo hili pia inaweza walionyesha katika fomu factored kama\(20x (3x−2)\; \text{units}^2\). Tunaweza kuthibitisha kwamba hii ni kujieleza sawa kwa kuzidisha.

Maneno mengi ya polynomial yanaweza kuandikwa kwa fomu rahisi kwa kuzingatia. Katika sehemu hii, tutaangalia mbinu mbalimbali ambazo zinaweza kutumika kwa sababu ya maneno ya polynomial.

Kufanya sababu kubwa ya kawaida ya Polynomial

Tunapojifunza sehemu ndogo, tunajifunza kuwa sababu kubwa zaidi (GCF) ya namba mbili ni idadi kubwa ambayo hugawanya sawasawa katika namba zote mbili. Kwa mfano,\(4\) ni GCF ya\(16\) na\(20\) kwa sababu ni idadi kubwa ambayo hugawanya sawasawa katika wote\(16\) na\(20\) GCF ya polynomials kazi kwa njia sawa:\(4x\) ni GCF ya\(16x\) na\(20x^2\) kwa sababu ni polynomial kubwa kwamba mgawanyiko sawasawa katika wote wawili\(16x\) na\(20x^2\).

Wakati wa kutafakari maneno ya polynomial, hatua yetu ya kwanza inapaswa kuwa kuangalia kwa GCF. Angalia GCF ya coefficients, na kisha utafute GCF ya vigezo.

Ufafanuzi: Sababu kuu ya kawaida

Sababu kubwa zaidi ya kawaida (GCF) ya polynomials ni polynomial kubwa ambayo hugawanya sawasawa katika polynomials.

Jinsi ya: Kutokana na kujieleza polynomial, sababu nje ya sababu kubwa ya kawaida

Tambua GCF ya coefficients.
Tambua GCF ya vigezo.
Kuchanganya ili kupata GCF ya kujieleza.
Kuamua nini GCF inahitaji kuzidishwa na kupata kila neno katika kujieleza.
Andika kujieleza kwa sababu kama bidhaa ya GCF na jumla ya maneno tunayohitaji kuzidisha.

Mfano\(\PageIndex{1}\): Factoring the Greatest Common Factor

Factor\(6x^3y^3 +45x^2y^2+21xy\).

Suluhisho

Kwanza, tafuta GCF ya maneno. GCF ya\(6\),\(45\), na\(21\) ni\(3\). GCF ya\(x^3\),\(x^2\), na\(x\) ni\(x\). (Kumbuka kuwa GCF ya seti ya maneno katika fomu daima\(x^n\) kuwa exponent ya shahada ya chini.) Na GCF ya\(y^3\),\(y^2\), na\(y\) ni\(y\). Kuchanganya hizi ili kupata GCF ya polynomial,\(3xy\).

Kisha, tambua nini GCF inahitaji kuzidishwa na kupata kila muda wa polynomial. Tunaona kwamba

\(3xy(2x^2y^2)=6x^3y^3\),
\(3xy(15xy)=45x^2y^2\), na
\(3xy(7)=21xy\).

Hatimaye, kuandika kujieleza factored kama bidhaa ya GCF na jumla ya maneno tuliyohitaji kuzidisha na.

\[(3xy)(2x^2y^2+15xy+7) \nonumber\]

Uchambuzi

Baada ya kuzingatia, tunaweza kuangalia kazi yetu kwa kuzidisha. Tumia mali ya kusambaza ili kuthibitisha kwamba

\[(3xy)(2x^2y^2+15xy+7)=6x^3y^3+45x^2y^2+21xy \nonumber\]

Zoezi\(\PageIndex{1}\)

Sababu\(x(b^2−a)+6(b^2−a)\) kwa kuunganisha nje GCF.

Jibu: \((b^2−a)(x+6)\)

Kuzingatia Trinomial na Mgawo wa Uongozi 1

Ingawa tunapaswa daima kuanza kwa kutafuta GCF, kuunganisha nje GCF sio njia pekee ambayo maneno ya polynomial yanaweza kuhesabiwa. Polynomial\(x^2+5x+6\) ina GCF ya\(1\), lakini inaweza kuandikwa kama bidhaa ya mambo\((x+2)\) na\((x+3)\).

Trinomials ya fomu\(x^2+bx+c\) inaweza kuhesabiwa kwa kutafuta namba mbili na bidhaa ya\(c\) na jumla ya\(b\). Trinomial\(x^2+10x+16\), kwa mfano, inaweza kuhesabiwa kwa kutumia namba\(2\) na\(8\) kwa sababu bidhaa ya namba hizo ni\(16\) na jumla yao ni\(10\). Trinomial inaweza kuandikwa upya kama bidhaa ya\((x+2)\) na\((x+8)\).

KUZINGATIA TRINOMIAL NA MGAWO WA KUONGOZA\(1\)

Trinomial ya fomu\(x^2+bx+c\) inaweza kuandikwa kwa fomu ya sababu kama\((x+p)(x+q)\) wapi\(pq=c\) na\(p+q=b\).

Q & A: Je, kila trinomial inaweza kuchukuliwa kama bidhaa ya binomials?

Hapana. Baadhi ya polynomials haiwezi kuelezewa. Polynomials hizi zinasemekana kuwa mkuu.

Jinsi ya: Kutokana na trinomial katika fomu\(x^2+bx+c\), factor it

Orodha ya mambo ya\(c\).
Kupata\(p\) na\(q\), jozi ya mambo ya\(c\) pamoja na jumla ya\(b\).
Andika kujieleza kwa sababu\((x+p)(x+q)\).

Mfano\(\PageIndex{2}\): Factoring a Trinomial with Leading Coefficient 1

Factor\(x^2+2x−15\).

Suluhisho

Tuna trinomial na mgawo wa kuongoza\(1\),\(b=2\), na\(c=−15\). Tunahitaji kupata namba mbili na bidhaa ya\(−15\) na jumla ya\(2\). Katika Jedwali\(\PageIndex{1}\), tunaorodhesha mambo mpaka tunapata jozi na jumla ya taka.

Jedwali\(\PageIndex{1}\)
Mambo ya -15	Jumla ya Mambo
1, -15	-14
—1,15	14
3, -5	-2
-3,5

Sasa kwa kuwa tuna kutambuliwa\(p\)\(−3\) na\(q\) kama na\(5\), kuandika fomu factored kama\((x−3)(x+5)\).

Uchambuzi

Tunaweza kuangalia kazi yetu kwa kuzidisha. Tumia FOIL ili kuthibitisha hilo\((x−3)(x+5)=x^2+2x−15\).

Q & A: Je, utaratibu wa mambo ni jambo?

Hapana. Kuzidisha ni commutative, hivyo utaratibu wa mambo haijalishi.

Zoezi\(\PageIndex{2}\)

Factor\(x^2−7x+6\).

Jibu: \((x−6)(x−1)\)

Kuzingatia kwa Kundi

Trinomials na coefficients inayoongoza zaidi ya\(1\) ni ngumu zaidi kwa sababu. Kwa hizi trinomials, tunaweza sababu kwa kambi kwa kugawa neno x katika jumla ya maneno mawili, factoring kila sehemu ya kujieleza tofauti, na kisha factoring nje GCF ya kujieleza nzima. Trinomial\(2x^2+5x+3\) inaweza kuandikwa upya kama\((2x+3)(x+1)\) kutumia mchakato huu. Tunaanza kwa kuandika tena usemi wa awali kama\(2x^2+2x+3x+3\) na kisha sababu kila sehemu ya kujieleza ili kupata\(2x(x+1)+3(x+1)\). Sisi kisha kuvuta nje GCF ya kupata\((x+1)\) kujieleza factored.

Kipengele kwa Kundi

Ili kuzingatia trinomial katika fomu\(ax^2+bx+c\) kwa kikundi, tunapata namba mbili na bidhaa\(ac\) na jumla ya\(b\). Tunatumia namba hizi kugawanya\(x\) neno katika jumla ya maneno mawili na sababu kila sehemu ya kujieleza tofauti, kisha fikiria nje GCF ya kujieleza nzima.

Jinsi ya: Kutokana na trinomial katika fomu\(ax^2+bx+c\), factor by grouping.

Orodha ya mambo ya\(ac\).
Kupata\(p\) na\(q\), jozi ya mambo ya\(ac\) pamoja na jumla ya\(b\).
Andika upya usemi wa awali kama\(ax^2+px+qx+c\).
Kuvuta nje GCF ya\(ax^2+px\).
Kuvuta nje GCF ya\(qx+c\).
Factor nje GCF ya kujieleza.

Mfano\(\PageIndex{3}\): Factoring a Trinomial by Grouping

Sababu\(5x^2+7x−6\) kwa kikundi.

Suluhisho

Tuna trinomial na\(a=5\),\(b=7\), na\(c=−6\). Kwanza, tambua\(ac=−30\). Tunahitaji kupata namba mbili na bidhaa ya\(−30\) na jumla ya\(7\). Katika meza hapa chini, tunaorodhesha mambo mpaka tunapata jozi na jumla ya taka.

Jedwali\(\PageIndex{2}\)
Mambo ya -30	Jumla ya Mambo
1, -30	-29
-1,30	29
2, -15	—13
—2,15	13
3, -10	-7
-3,10	7

Hivyo\(p=−3\) na\(q=10\).

\(5x^2−3x+10x−6\)Andika upya usemi wa awali kama\(ax^2+px+qx+c\).

\(x(5x−3)+2(5x−3)\)Factor nje GCF ya kila sehemu

\((5x−3)(x+2)\)Factor nje GCF ya kujieleza.

Uchambuzi

Tunaweza kuangalia kazi yetu kwa kuzidisha. Tumia FOIL ili kuthibitisha hilo\((5x−3)(x+2)=5x^2+7x−6\).

Zoezi\(\PageIndex{3}\)

Sababu:

\(2x^2+9x+9\)
\(6x^2+x−1\)

Jibu: \((2x+3)(x+3)\)
Jibu b: \((3x-1)(2x+1)\)

Kufanya Mraba Mzuri wa Utatu

Mraba kamili ya trinomial ni trinomial ambayo inaweza kuandikwa kama mraba wa binomial. Kumbuka kwamba wakati binomial ni mraba, matokeo yake ni mraba wa muda wa kwanza aliongeza kwa mara mbili bidhaa ya maneno mawili na mraba wa muda wa mwisho.

\[a^2+2ab+b^2={(a+b)}^2\]

\[a^2-2ab+b^2={(a-b)}^2\]

Tunaweza kutumia equation hii kwa sababu yoyote kamili mraba trinomial.

Perfect Square Trinomials

Mraba kamili ya trinomial inaweza kuandikwa kama mraba wa binomial:

\[a^2+2ab+b^2=(a+b)^2\]

Jinsi ya: Kutokana na trinomial mraba kamili, factor ndani ya mraba wa binomial

Thibitisha kwamba muda wa kwanza na wa mwisho ni mraba kamilifu.
Thibitisha kwamba muda wa kati ni mara mbili ya bidhaa ya\(ab\).
Andika fomu iliyosababishwa kama\({(a+b)}^2\).

Mfano\(\PageIndex{4}\): Factoring a Perfect Square Trinomial

Factor\(25x^2+20x+4\).

Suluhisho

Kumbuka kwamba\(25x^2\) na\(4\) ni mraba kamili kwa sababu\(25x^2={(5x)}^2\) na\(4=2^2\). Kisha angalia ili uone kama muda wa kati ni mara mbili ya bidhaa\(5x\) na\(2\). Muda wa kati ni, kwa kweli, mara mbili ya bidhaa:\(2(5x)(2)=20x\). Kwa hiyo, trinomial ni trinomial kamili ya mraba na inaweza kuandikwa kama\({(5x+2)}^2\).

Zoezi\(\PageIndex{4}\)

Factor\(49x^2−14x+1\).

Jibu: \({(7x−1)}^2\)

Kuzingatia Tofauti ya Viwanja

Tofauti ya mraba ni mraba kamilifu iliyotolewa kutoka mraba kamilifu. Kumbuka kwamba tofauti ya mraba inaweza kuandikwa upya kama sababu zenye maneno sawa lakini ishara kinyume kwa sababu maneno ya kati kufuta kila mmoja nje wakati mambo mawili ni kuzidisha.

\[a^2−b^2=(a+b)(a−b)\]

Tunaweza kutumia equation hii kwa sababu tofauti yoyote ya mraba.

Tofauti ya Viwanja

Tofauti ya mraba inaweza kuandikwa upya kama mambo mawili yaliyo na maneno sawa lakini ishara tofauti.

\[a^2−b^2=(a+b)(a−b)\]

Jinsi ya: Kutokana na tofauti ya mraba, fanya ndani ya binomials

Thibitisha kwamba muda wa kwanza na wa mwisho ni mraba kamilifu.
Andika fomu iliyosababishwa kama\((a+b)(a−b)\).

Mfano\(\PageIndex{5}\): Factoring a Difference of Squares

Factor\(9x^2−25\).

Suluhisho

Kumbuka kwamba\(9x^2\) na\(25\) ni mraba kamili kwa sababu\(9x^2={(3x)}^2\) na\(25=5^2\). Polynomial inawakilisha tofauti ya mraba na inaweza kuandikwa upya kama\((3x+5)(3x−5)\).

Zoezi\(\PageIndex{5}\)

Factor\(81y^2−100\).

Jibu: \((9y+10)(9y−10)\)

Q & A: Je, kuna formula kwa sababu jumla ya mraba?

Hapana. Jumla ya mraba haiwezi kufananishwa.

Kuzingatia Jumla na Tofauti ya Cubes

Sasa, tutaangalia bidhaa mbili mpya maalum: jumla na tofauti ya cubes. Ingawa jumla ya mraba haiwezi kuhesabiwa, jumla ya cubes inaweza kuhesabiwa kuwa binomial na trinomial.

\[a^3+b^3=(a+b)(a^2−ab+b^2)\]

Vile vile, jumla ya cubes inaweza kuhesabiwa katika binomial na trinomial, lakini kwa ishara tofauti.

\[a^3−b^3=(a−b)(a^2+ab+b^2)\]

Tunaweza kutumia SOAP kifupi kukumbuka ishara wakati factoring jumla au tofauti ya cubes. Barua ya kwanza ya kila neno inahusiana na ishara: Same Inapingana Daima Chanya. Kwa mfano, fikiria mfano unaofuata.

\[x^3−2^3=(x−2)(x^2+2x+4)\]

Ishara ya 2 ya kwanza ni sawa na ishara kati ya\(x^3−2^3\). Ishara ya\(2x\) neno ni kinyume na ishara kati ya\(x^3−2^3\). Na ishara ya muda wa mwisho,\(4\), daima ni chanya.

Jumla na Tofauti ya Cubes

Tunaweza sababu jumla ya cubes mbili kama

\[a^3+b^3=(a+b)(a^2−ab+b^2)\]

Tunaweza sababu tofauti ya cubes mbili kama

\[a^3−b^3=(a−b)(a^2+ab+b^2)\]

Jinsi ya: Kutokana na jumla ya cubes au tofauti ya cubes, factor it

Thibitisha kwamba muda wa kwanza na wa mwisho ni cubes,\(a^3+b^3\) au\(a^3−b^3\).
Kwa jumla ya cubes, kuandika fomu factored kama\((a+b)(a^2−ab+b^2)\). Kwa tofauti ya cubes, andika fomu iliyowekwa kama\((a−b)(a^2+ab+b^2)\).

Mfano\(\PageIndex{6}\): Factoring a Sum of Cubes

Factor\(x^3+512\).

Suluhisho

Kumbuka kwamba\(x^3\) na\(512\) ni cubes kwa sababu\(8^3=512\). Andika upya jumla ya cubes kama\((x+8)(x^2−8x+64)\).

Uchambuzi

Baada ya kuandika jumla ya cubes kwa njia hii, tunaweza kufikiri tunapaswa kuangalia ili kuona kama sehemu ya trinomial inaweza kuwa factored zaidi. Hata hivyo, sehemu ya trinomial haiwezi kuhesabiwa, kwa hivyo hatuhitaji kuangalia.

Zoezi\(\PageIndex{6}\)

Factor jumla ya cubes:\(216a^3+b^3\).

Jibu: \((6a+b)(36a^2−6ab+b^2)\)

Mfano\(\PageIndex{7}\): Factoring a Difference of Cubes

Factor\(8x^3−125\).

Suluhisho

Kumbuka kwamba\(8x^3\) na\(125\) ni cubes kwa sababu\(8x^3={(2x)}^3\) na\(125=5^3\). Andika tofauti ya cubes kama\((2x−5)(4x^2+10x+25)\).

Uchambuzi

Kama ilivyo kwa jumla ya cubes, hatuwezi kuimarisha sehemu ya trinomial.

Zoezi\(\PageIndex{7}\)

Fanya tofauti ya cubes:\(1000x^3−1\)

Jibu: \((10x−1)(100x^2+10x+1)\)

Maneno ya kutafakari na vielelezo vya Fractional au Hasi

Maneno yenye vielelezo vya sehemu au hasi yanaweza kuzingatiwa kwa kuunganisha GCF. Angalia kwa variable au exponent kwamba ni kawaida kwa kila muda wa kujieleza na kuvuta nje kwamba variable au exponent alimfufua kwa nguvu ya chini kabisa. Maneno haya yanafuata sheria sawa za factoring kama wale walio na exponents integer. Kwa mfano,\(2x^{\tfrac{1}{4}}+5x^{\tfrac{3}{4}}\) inaweza kuwa factored kwa kuunganisha nje\(x^{\tfrac{1}{4}}\) na kuandikwa upya kama\(x^{\tfrac{1}{4}}(2+5x^{\tfrac{1}{2}})\).

Mfano\(\PageIndex{8}\): Factoring an Expression with Fractional or Negative Exponents

Factor\(3x{(x+2)}^{-\tfrac{1}{3}}+4{(x+2)}^{\tfrac{2}{3}}\).

Suluhisho

Factor nje mrefu na thamani ya chini ya exponent. Katika kesi hiyo, hiyo itakuwa\({(x+2)}^{-\tfrac{1}{3}}\).

\[\begin{align*} &(x+2)^{-\tfrac{1}{3}}(3x+4(x+2))\qquad \text{Factor out the GCF }\\ &(x+2)^{-\tfrac{1}{3}}(3x+4x+8)\qquad \text{Simplify } \\ &(x+2)^{-\tfrac{1}{3}}(7x+8) \end{align*}\]

Zoezi\(\PageIndex{8}\)

Factor\(2{(5a−1)}^{\tfrac{3}{4}}+7a{(5a−1)}^{−\tfrac{1}{4}}\).

Jibu: \({(5a−1)}^{−\tfrac{1}{4}}(17a−2)\)

vyombo vya habari

Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na factoring polynomials.

1. Tambua GCF

2. Factor Trinomials wakati Sawa 1

3. Factor Trinomials wakati si sawa na 1

4. Kiasi cha Kiasi au Tofauti ya Cubes

Mlinganyo muhimu

tofauti ya mraba	\(a^2−b^2=(a+b)(a−b)\)
mraba kamili trinomial	\(a^2+2ab+b^2=(a+b)^2\)
jumla ya cubes	\(a^3+b^3=(a+b)(a^2−ab+b^2)\)
tofauti ya cubes	\(a^3−b^3=(a−b)(a^2+ab+b^2)\)

Sababu kubwa ya kawaida, au GCF, inaweza kuhesabiwa nje ya polynomial. Kuangalia kwa GCF lazima hatua ya kwanza katika tatizo lolote factoring. Angalia Mfano.
Trinomials na mgawo wa kuongoza 1 inaweza kuhesabiwa kwa kutafuta namba zilizo na bidhaa ya muda wa tatu na jumla ya muda wa pili. Angalia Mfano.
Trinomials inaweza kuhesabiwa kwa kutumia mchakato unaoitwa factoring kwa kikundi. Angalia Mfano.
Vipande vya mraba kamili na tofauti za mraba ni bidhaa maalum na zinaweza kuzingatiwa kwa kutumia equations. Angalia Mfano na Mfano.
Jumla ya cubes na tofauti ya cubes inaweza kuhesabiwa kwa kutumia equations. Angalia Mfano na Mfano.
Polynomials zenye vielelezo vya sehemu na hasi vinaweza kuhesabiwa kwa kuunganisha GCF. Angalia Mfano.