1.5: Polynomials
- Page ID
- 180805
Katika sehemu hii wanafunzi:
- Tambua kiwango na mgawo wa kuongoza wa polynomials.
- Ongeza na uondoe polynomials.
- Kuzidisha polynomials.
- Tumia FOIL kuzidisha binomials.
- Fanya shughuli na polynomia
- ls ya vigezo kadhaa.
Earl anajenga nyumba ya mbwa, ambaye mbele yake iko katika sura ya mraba uliojaa pembetatu. Kutakuwa na mlango wa mstatili ambao mbwa anaweza kuingia na kuondoka nyumbani. Earl anataka kupata eneo la mbele ya nyumba ya mbwa ili aweze kununua kiasi sahihi cha rangi. Kutumia vipimo vya mbele ya nyumba, iliyoonyeshwa kwenye Kielelezo\(\PageIndex{1}\), tunaweza kuunda maneno ambayo yanachanganya maneno kadhaa ya kutofautiana, kutuwezesha kutatua tatizo hili na wengine kama hayo.
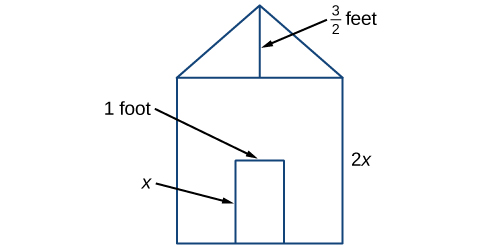
- Kwanza kupata eneo la mraba katika miguu ya mraba.
\[\begin{align*} A &= s^2\\ &= {(2x)}^2\\ &= 4x^2 \end{align*}\]
- Kisha tafuta eneo la pembetatu katika miguu ya mraba.
\[\begin{align*} A &= \dfrac{1}{2}bh\\ &= \dfrac{1}{2}(2x)\left (\dfrac{3}{2} \right )\\ &= \dfrac{3}{2}x \end{align*}\]
- Kisha kupata eneo la mlango wa mstatili katika miguu ya mraba.
\[\begin{align*} A &= lw\\ &= x\times1\\ &= x \end{align*}\]
Eneo la mbele la mbwa linaweza kupatikana kwa kuongeza maeneo ya mraba na pembetatu, na kisha kuondoa eneo la mstatili. Tunapofanya hivyo, tunapata
\(4x^2+\dfrac{3}{2}x-x\)\(ft^2\)
au
\(4x^2+\dfrac{1}{2}x\)\(ft^2\)
Katika sehemu hii, tutachunguza maneno kama haya, ambayo yanachanganya maneno kadhaa ya kutofautiana.
Kutambua Shahada na Uongozi wa Mgawo wa Polynomials
Fomu iliyopatikana tu ni mfano wa polynomial, ambayo ni jumla ya au tofauti ya maneno, kila yenye variable iliyofufuliwa kwa nguvu isiyo ya negative integer. Nambari inayoongezeka kwa kutofautiana iliyoinuliwa kwa exponent, kama vile\(384\pi\), inajulikana kama mgawo. Coefficients inaweza kuwa chanya, hasi, au sifuri, na inaweza kuwa namba nzima, decimals, au sehemu ndogo. Kila bidhaa\(a_ix^i\), kama vile\(384\pi w\), ni neno la polynomial. Kama neno haina variable, inaitwa mara kwa mara.
Polynomial iliyo na muda mmoja tu, kama vile\(5x^4\), inaitwa monomial. Polynomial iliyo na maneno mawili, kama vile\(2x−9\), inaitwa binomial. Polynomial iliyo na maneno matatu\(−3x^2+8x−7\), kama vile, inaitwa trinomial.
Tunaweza kupata shahada ya polynomial kwa kutambua nguvu ya juu ya variable ambayo hutokea katika polynomial. Neno lenye shahada ya juu linaitwa neno la kuongoza kwa sababu kwa kawaida linaandikwa kwanza. Mgawo wa neno la kuongoza huitwa mgawo wa kuongoza. Wakati polynomial imeandikwa ili nguvu zishuka, tunasema kuwa ni katika fomu ya kawaida.
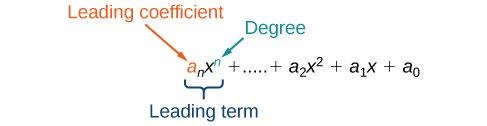
Polynomial ni maneno ambayo yanaweza kuandikwa kwa fomu
Kila namba halisi ai inaitwa mgawo. Nambari\(a_0\) ambayo haijazidishwa na variable inaitwa mara kwa mara. Kila bidhaa\(a_ix^i\) ni neno la polynomial. Nguvu ya juu ya variable ambayo hutokea katika polynomial inaitwa shahada ya polynomial. Neno la kuongoza ni neno na nguvu ya juu, na mgawo wake huitwa mgawo wa kuongoza.
- Kupata nguvu ya juu ya x kuamua shahada.
- Tambua neno lenye nguvu ya juu ya x ili kupata neno linaloongoza.
- Tambua mgawo wa muda unaoongoza.
Kwa polynomials zifuatazo, kutambua shahada, muda wa kuongoza, na mgawo wa kuongoza.
- \(3+2x^2−4x^3\)
- \(5t^5−2t^3+7t\)
- \(6p−p^3−2\)
Suluhisho
- Nguvu ya juu zaidi\(x\) ni\(3\), hivyo shahada ni\(3\). Neno la kuongoza ni neno lenye shahada hiyo,\(−4x^3\). Mgawo wa kuongoza ni mgawo wa muda huo,\(−4\).
- Nguvu ya juu zaidi\(t\) ni\(5\), hivyo shahada ni\(5\). Neno la kuongoza ni neno lenye shahada hiyo,\(5t^5\). Mgawo wa kuongoza ni mgawo wa muda huo,\(5\).
- Nguvu ya juu zaidi\(p\) ni\(3\), hivyo shahada ni\(3\). Neno la kuongoza ni neno lenye shahada hiyo,\(−p^3\), Mgawo wa kuongoza ni mgawo wa muda huo, -1.
Tambua shahada, muda wa kuongoza, na mgawo wa kuongoza wa polynomial\(4x^2−x^6+2x−6\).
- Jibu
-
Kiwango ni\(6\), neno la kuongoza ni\(−x^6\), na mgawo wa kuongoza ni\(−1\).
Kuongeza na Kutoa Polynomials
Tunaweza kuongeza na Ondoa polynomials kwa kuchanganya kama maneno, ambayo ni maneno ambayo yana vigezo sawa alimfufua kwa exponents sawa. Kwa mfano,\(5x^2\) na\(−2x^2\) ni kama maneno, na inaweza kuongezwa kupata\(3x^2\), lakini\(3x\) na\(3x^2\) si kama maneno, na kwa hiyo haiwezi kuongezwa.
- Kuchanganya kama maneno.
- Kurahisisha na kuandika kwa fomu ya kawaida.
Pata jumla.
\((12x^2+9x−21)+(4x^3+8x^2−5x+20)\)
Suluhisho
\[\begin{align*} &4x^3+(12x^2+8x^2)+(9x-5x)+(-21+20)\qquad \text{Combine like terms} \\ &4x^3+20x^2+4x-1\qquad \qquad \qquad \qquad \qquad \qquad \; \; \; \text{Simplify} \end{align*}\]
Uchambuzi
Tunaweza kuangalia majibu yetu kwa aina hizi za matatizo kwa kutumia calculator graphing. Kuangalia, graph tatizo kama iliyotolewa pamoja na jibu kilichorahisishwa. Grafu mbili zinapaswa kuwa sawa. Hakikisha kutumia dirisha moja ili kulinganisha grafu. Kutumia madirisha tofauti kunaweza kufanya maneno yanaonekana sawa wakati haipo.
Pata jumla.
\((2x^3+5x^2−x+1)+(2x^2−3x−4)\)
- Jibu
-
\(2x^3+7x^2−4x−3\)
Kupata tofauti.
\((7x^4−x^2+6x+1)−(5x^3−2x^2+3x+2)\)
Suluhisho
\(7x^4−5x^3+(−x^2+2x^2)+(6x−3x)+(1−2)\)Kuchanganya kama maneno
\(7x^4−5x^3+x^2+3x−1\)Kurahisisha
Uchambuzi
Kumbuka kuwa kutafuta tofauti kati ya polynomials mbili ni sawa na kuongeza kinyume cha polynomial pili kwa kwanza.
Kupata tofauti.
\((−7x^3−7x^2+6x−2)−(4x^3−6x^2−x+7)\)
- Jibu
-
\(−11x^3−x^2+7x−9\)
Kuzidisha Polynomials
Kuzidisha polynomials ni changamoto kidogo zaidi kuliko kuongeza na kuondoa polynomials. Tunapaswa kutumia mali ya usambazaji ili kuzidisha kila neno katika polynomial ya kwanza kwa kila neno katika polynomial ya pili. Sisi kisha kuchanganya kama maneno. Tunaweza pia kutumia njia ya mkato inayoitwa njia ya FOIL wakati wa kuzidisha binomials. Baadhi ya bidhaa maalum hufuata ruwaza ambazo tunaweza kukariri na kutumia badala ya kuzidisha polynomials kwa mkono kila wakati. Tutaangalia njia mbalimbali za kuzidisha polynomials.
Kuzidisha Polynomials Kutumia Mali ya Kusambaza
Ili kuzidisha idadi kwa polynomial, tunatumia mali ya usambazaji. Nambari inapaswa kusambazwa kwa kila muda wa polynomial. Tunaweza kusambaza\(2\) katika\(2(x+7)\) kupata kujieleza sawa\(2x+14\). Wakati wa kuzidisha polynomials, mali ya usambazaji inatuwezesha kuzidisha kila neno la polynomial ya kwanza kwa kila muda wa pili. Sisi kisha kuongeza bidhaa pamoja na kuchanganya kama maneno kurahisisha.
- Panua kila neno la polynomial ya kwanza kwa kila muda wa pili.
- Kuchanganya kama maneno.
- Kurahisisha.
Pata bidhaa.
\((2x+1)(3x^2−x+4)\)
Suluhisho
\[\begin{align*} &2x(3x^2-x+4)+1(3x^2-x+4)\qquad \text{ Use the distributive property }\\ &(6x^3-2x^2+8x)+(3x^2-x+4)\qquad \text{ Multiply }\\ &6x^3+(-2x^2+3x^2)+(8x-x)+4\qquad \text{ Combine like terms } \\ &6x^3+x^2+7x+4\qquad \text{ Simplify } \end{align*}\]
Uchambuzi
Tunaweza kutumia meza kuweka wimbo wa kazi yetu, kama inavyoonekana katika Jedwali\(\PageIndex{1}\). Andika polynomial moja juu na nyingine chini upande. Kwa kila sanduku katika meza, kuzidisha mrefu kwa mstari huo kwa muda kwa safu hiyo. Kisha kuongeza maneno yote pamoja, kuchanganya kama maneno, na kurahisisha.
| \(3x^2\) | \(−x\) | \(+4\) | |
| \(2x\) | \(6x^3\) | \(−2x^2\) | \(8x\) |
| \(+1\) | \(3x^2\) | \(−x\) | \(4\) |
Pata bidhaa.
\((3x+2)(x^3−4x^2+7)\)
- Jibu
-
\(3x^4−10x^3−8x^2+21x+14\)
Kutumia FOIL kuzidisha Binomials
Njia ya mkato inayoitwa FOIL wakati mwingine hutumiwa kupata bidhaa ya binomials mbili. Inaitwa FOIL kwa sababu tunazidisha maneno ya kwanza, maneno ya nje, maneno ya ndani, na kisha maneno ya mwisho ya kila binomial.

Njia ya FOIL inatoka nje ya mali ya usambazaji. Sisi ni tu kuzidisha kila neno la binomial kwanza kwa kila muda wa binomial pili, na kisha kuchanganya kama maneno.
Kutokana na binomials mbili, tumia FOIL ili kurahisisha maneno.
- Panua maneno ya nje ya binomials.
- Panua maneno ya mwisho ya kila binomial.
- Kuchanganya kama maneno na kurahisisha.
Tumia FOIL ili kupata bidhaa.
\((2x−10)(3x+3) \nonumber\)
Suluhisho
Pata bidhaa ya maneno ya kwanza.

Pata bidhaa ya maneno ya nje.

Pata bidhaa ya maneno ya ndani.

Pata bidhaa ya masharti ya mwisho.

\[\begin{align*} &6x^2+6x-54x-54\qquad \text{Add the products}\\ &6x^2+(6x-54x)-54\qquad \text{Combine like terms} \\ &6x^2-48x-54\qquad \qquad \qquad \text{Simplify} \end{align*}\]
Tumia FOIL ili kupata bidhaa.
\((x+7)(3x−5)\)
- Jibu
-
\(3x^2+16x−35\)
Perfect Square Trinomials
Bidhaa fulani za binomial zina aina maalum. Wakati binomial ni mraba, matokeo huitwa trinomial kamili ya mraba. Tunaweza kupata mraba kwa kuzidisha binomial yenyewe. Hata hivyo, kuna fomu maalum ambayo kila moja ya trinomials hizi za mraba kamili huchukua, na kukariri fomu hufanya binomials ya mraba iwe rahisi zaidi na kwa kasi. Hebu tuangalie trinomials chache za mraba kamili ili kujitambulisha na fomu.
\({(x+5)}^2=x^2+10x+25\)
\({(x-3)}^2=x^2-6x+9\)
Kumbuka kwamba muda wa kwanza wa kila trinomial ni mraba wa muda wa kwanza wa binomial na, sawa, muda wa mwisho wa kila trinomial ni mraba wa muda wa mwisho wa binomial. Muda wa kati ni mara mbili ya bidhaa za maneno mawili. Hatimaye, tunaona kwamba ishara ya kwanza ya trinomial ni sawa na ishara ya binomial.
Wakati binomial ni mraba, matokeo ni muda wa kwanza squared aliongeza kwa mara mbili bidhaa ya maneno yote na muda wa mwisho squared.
\[{(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2\]
- Square muda wa kwanza wa binomial.
- Square muda wa mwisho wa binomial.
- Kwa muda wa kati wa trinomial, mara mbili ya bidhaa ya maneno mawili.
- Kuongeza na kurahisisha.
Panua\((3x−8)^2\).
Suluhisho
Anza kwa kueneza muda wa kwanza na muda wa mwisho. Kwa muda wa kati wa trinomial, mara mbili ya bidhaa ya maneno mawili.
\[\begin{align*} &{(3x)}^2-2(3x)(8)+{(-8)}^2 \\ &9x^2-48x+64\qquad \qquad \; \; \; \; \text{Simplify} \end{align*}\]
Panua\({(4x−1)}^2\).
- Jibu
-
\(16x^2−8x+1\)
Tofauti ya Viwanja
Bidhaa nyingine maalum inaitwa tofauti ya mraba, ambayo hutokea tunapozidisha binomial na binomial nyingine kwa maneno sawa lakini ishara tofauti. Hebu tuone kinachotokea wakati tunapozidisha\((x+1)(x−1)\) kutumia njia ya FOIL.
\[\begin{align*} (x+1)(x-1) &= x^2-x+x-1\\ &= x^2-1 \end{align*}\]
Muda wa kati hutoka nje, na kusababisha tofauti ya mraba. Kama tulivyofanya na mraba kamili, hebu tuangalie mifano michache.
\((x+5)(x-5)=x^2-25\)
\((x+11)(x-11)=x^2-121\)
\((2x+3)(2x-3)=4x^2-9\)
Kwa sababu ishara inabadilika katika binomial ya pili, maneno ya nje na ya ndani yanaghairi nje, na tunaachwa tu na mraba wa muda wa kwanza usiondoe mraba wa muda wa mwisho.
Je, kuna fomu maalum kwa jumla ya mraba?
Hapana. Tofauti ya mraba hutokea kwa sababu ishara tofauti za binomials husababisha maneno ya kati kutoweka. Hakuna binomials mbili zinazozidisha kwa sawa jumla ya mraba.
Wakati binomial inavyoongezeka na binomial na maneno sawa yaliyotengwa na ishara tofauti, matokeo yake ni mraba wa muda wa kwanza bala mraba wa muda wa mwisho.
\[(a+b)(a−b)=a^2−b^2\]
- Square muda wa kwanza wa binomials.
- Square muda wa mwisho wa binomials.
- Ondoa mraba wa muda wa mwisho kutoka mraba wa muda wa kwanza.
Kuzidisha\((9x+4)(9x−4)\).
Suluhisho
Square muda wa kwanza kupata\({(9x)}^2=81x^2\). Square muda wa mwisho wa kupata\(4^2=16\). Ondoa mraba wa muda wa mwisho kutoka mraba wa muda wa kwanza ili kupata bidhaa za\(81x^2−16\).
Kuzidisha\((2x+7)(2x−7)\).
- Jibu
-
\(4x^2−49\)
Kufanya Operesheni na Polynomials ya Vigezo kadhaa
Tumeangalia polynomials zenye variable moja tu. Hata hivyo, polynomial inaweza kuwa na vigezo kadhaa. Sheria zote hizo zinatumika wakati wa kufanya kazi na polynomials zenye vigezo kadhaa. Fikiria mfano:
\[\begin{align*} &(a+2b)(4a-b-c) a(4a-b-c)+2b(4a-b-c)\qquad \text{ Use the distributive property }\\ &4a^2-ab-ac+8ab-2b^2-2bc\qquad \qquad\qquad\qquad\qquad \text{ Multiply }\\ &4a^2+(-ab+8ab)-ac-2b^2-2bc\qquad \qquad\qquad\qquad \; \text{ Combine like terms } \\ &4a^2+7ab-ac-2bc-2b^2\qquad \qquad \qquad \qquad \qquad \qquad\text{ Simplify } \end{align*}\]
Kuzidisha\((x+4)(3x−2y+5)\).
Suluhisho
\[\begin{align*} &x(3x-2y+5)+4(3x-2y+5)\qquad \text{ Use the distributive property }\\ &3x^2-2xy+5x+12x-8y+20\qquad \text{ Multiply }\\ &3x^2-2xy+(5x+12x)-8y+20\qquad \text{ Combine like terms } \\ &3x^2-2xy+17x-8y+20\qquad \qquad\text{ Simplify } \end{align*}\]
Kuzidisha\((3x−1)(2x+7y−9)\).
- Jibu
-
\(6x^2+21xy−29x−7y+9\)
Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na polynomials.
Mlinganyo muhimu
| mraba kamili trinomial | \({(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2\) |
| tofauti ya mraba | \((a+b)(a−b)=a^2−b^2\) |
Dhana muhimu
- Polynomial ni jumla ya maneno kila yenye variable iliyofufuliwa kwa nguvu isiyo ya hasi integer. Kiwango ni nguvu ya juu ya kutofautiana ambayo hutokea katika polynomial. Neno la kuongoza ni neno lenye shahada ya juu, na mgawo wa kuongoza ni mgawo wa muda huo. Angalia Mfano.
- Tunaweza kuongeza na kuondoa polynomials kwa kuchanganya maneno kama hayo. Angalia Mfano na Mfano.
- Ili kuzidisha polynomials, tumia mali ya usambazaji ili kuzidisha kila neno katika polynomial ya kwanza kwa kila neno kwa pili. Kisha kuongeza bidhaa. Angalia Mfano.
- FOIL (Kwanza, Nje, Ndani, Mwisho) ni njia ya mkato ambayo inaweza kutumika kuzidisha binomials. Angalia Mfano.
- Trinomials mraba kamili na tofauti ya mraba ni bidhaa maalum. Angalia Mfano na Mfano.
- Fuata sheria sawa kufanya kazi na polynomials zenye vigezo kadhaa. Angalia Mfano.


