13.1: Pembe

Last updated
Save as PDF

Page ID: 181340

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Chora pembe katika nafasi ya kawaida.
Badilisha kati ya digrii na radians.
Pata pembe za coterminal.
Pata urefu wa arc ya mviringo.
Tumia kasi ya mstari na ya angular kuelezea mwendo kwenye njia ya mviringo.

Golfer swings hit mpira juu ya mtego mchanga na kwenye kijani. Jaribio la ndege linaloendesha ndege kuelekea barabara nyembamba. Muumbaji wa mavazi hujenga mtindo wa hivi karibuni. Je, wote wana sawa? Wote hufanya kazi kwa pembe, na hivyo tufanye sisi sote kwa wakati mmoja au mwingine. Wakati mwingine tunahitaji kupima pembe hasa na vyombo. Mara nyingine tunawahesabu au kuwahukumu kwa jicho. Kwa njia yoyote, angle sahihi inaweza kufanya tofauti kati ya mafanikio na kushindwa katika shughuli nyingi. Katika sehemu hii, tutachunguza mali ya pembe.

Kuchora Angles katika Nafasi ya kawaida

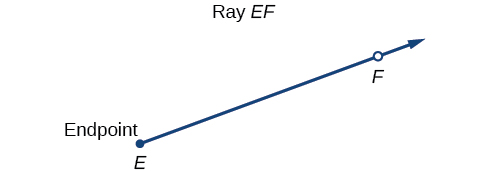
Kufafanua vizuri angle kwanza inahitaji kwamba tunafafanua ray. Ray ina hatua moja kwenye mstari na pointi zote zinazopanua katika mwelekeo mmoja kutoka hatua hiyo. Hatua ya kwanza inaitwa mwisho wa ray. Tunaweza kutaja ray maalum kwa kusema mwisho wake na hatua nyingine yoyote juu yake. Ray katika Kielelezo$\PageIndex{1}$ inaweza kuitwa kama ray EF, au kwa fomu ya ishara$\overrightarrow{EF}$.

Mfano wa Ray EF, na hatua F na mwisho E. — Kielelezo$\PageIndex{1}$

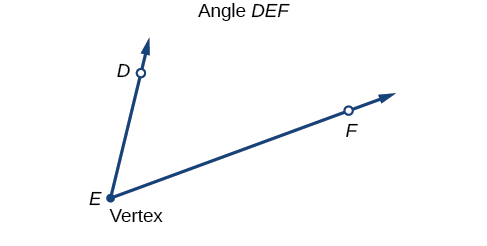
Pembe ni umoja wa mionzi miwili iliyo na mwisho wa kawaida. Mwisho huitwa vertex ya angle, na mionzi miwili ni pande za angle. Pembe katika Kielelezo$\PageIndex{2}$ huundwa kutoka$\overrightarrow{ED}$ na$\overrightarrow{EF}$. Angles inaweza kutajwa kwa kutumia uhakika juu ya kila ray na vertex, kama vile angle DEF, au katika fomu ya ishara$∠DEF.$

Mfano wa Angle DEF, na kipeo E na pointi D na F. — Kielelezo$\PageIndex{2}$

Herufi za Kigiriki mara nyingi hutumiwa kama vigezo kwa kipimo cha angle. Jedwali$\PageIndex{1}$ ni orodha ya barua Kigiriki kawaida kutumika kuwakilisha pembe, na angle sampuli ni inavyoonekana katika Kielelezo$\PageIndex{3}$.

Jedwali$\PageIndex{1}$
$θ$	$φ \text{ or }ϕ$	$α$	$β$	$γ$
theta	phi	alpha	beta	gamma

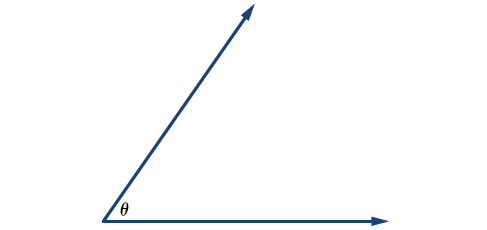
$Mfano wa theta angle.$

Kielelezo $\PageIndex{3}$: Angle theta, imeonyeshwa kama$∠θ$

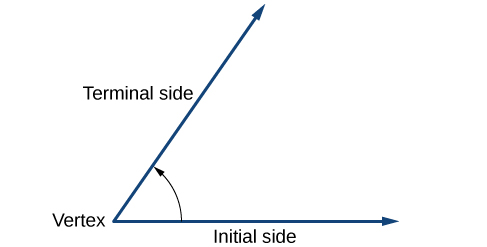
Uumbaji wa angle ni mchakato wa nguvu. Tunaanza na mionzi miwili iko juu ya kila mmoja. Tunaacha moja fasta mahali, na kugeuza nyingine. Ray fasta ni upande wa kwanza, na ray iliyozungushwa ni upande wa mwisho. Ili kutambua pande tofauti, tunaonyesha mzunguko na arc ndogo na mshale karibu na vertex kama kwenye Mchoro$\PageIndex{4}$.

Mfano wa angle na maandiko kwa upande wa awali, upande wa terminal, na vertex. — Kielelezo$\PageIndex{4}$

Kama tulivyojadiliwa mwanzoni mwa sehemu hiyo, kuna maombi mengi ya pembe, lakini ili tuitumie kwa usahihi, lazima tuweze kuzipima. Kipimo cha angle ni kiasi cha mzunguko kutoka upande wa awali hadi upande wa mwisho. Pengine kitengo cha kawaida zaidi cha kipimo cha angle ni shahada. Shahada moja ni$\frac{1}{360}$ ya mzunguko wa mviringo, hivyo mzunguko kamili wa mviringo una digrii 360. Pembe iliyopimwa kwa digrii lazima iwe pamoja na kitengo “digrii” baada ya namba, au ni pamoja na alama ya shahada°. Kwa mfano, digrii 90 = 90°.

Ili kurasimisha kazi yetu, tutaanza kwa kuchora pembe kwenye ndege ya kuratibu x - y. Angles zinaweza kutokea katika nafasi yoyote kwenye ndege ya kuratibu, lakini kwa lengo la kulinganisha, mkataba ni kuwaonyesha katika nafasi sawa wakati wowote iwezekanavyo. Pembe iko katika nafasi ya kawaida ikiwa vertex yake iko katika asili, na upande wake wa awali unaendelea pamoja na chanya x -axis. Angalia Kielelezo$\PageIndex{5}$.

Grafu ya angle katika nafasi ya kawaida na maandiko kwa upande wa awali na upande wa terminal. Upande wa awali huanza kwenye mhimili wa x na upande wa terminal iko katika Quadrant II na mshale wa kinyume cha kuunganisha mbili. — Kielelezo$\PageIndex{5}$

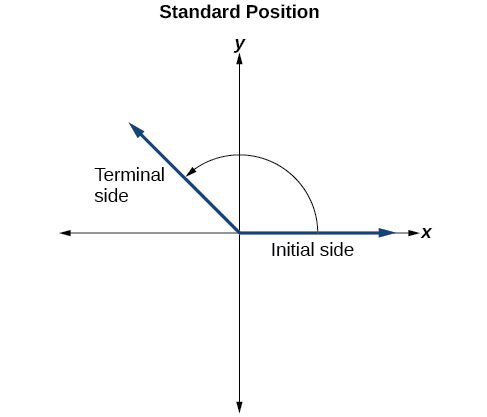
Ikiwa angle inapimwa kwa mwelekeo wa kinyume chake kutoka upande wa awali hadi upande wa terminal, angle inasemekana kuwa angle nzuri. Ikiwa angle inapimwa kwa mwelekeo wa saa, angle inasemekana kuwa angle hasi.

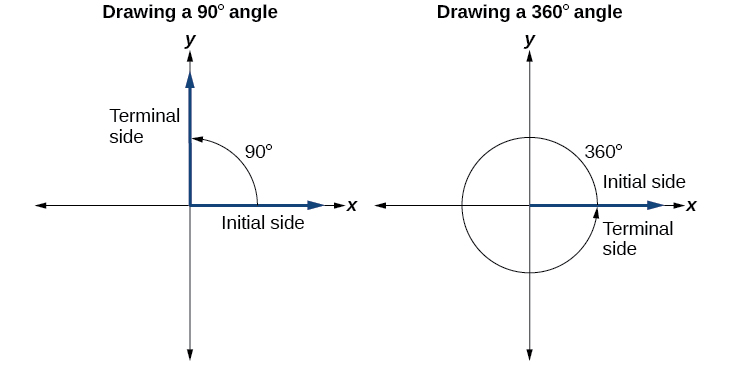
Kuchora angle katika nafasi ya kawaida daima huanza njia sawa-kuteka upande wa awali pamoja chanya x -axis. Ili kuweka upande wa mwisho wa angle, lazima tuhesabu sehemu ya mzunguko kamili angle inawakilisha. Tunafanya hivyo kwa kugawa kipimo cha angle kwa digrii kwa 360°. Kwa mfano, kuteka angle 90°, tunahesabu hiyo$\frac{90°}{360°}=\frac{1}{4}$. Kwa hiyo, upande wa terminal utakuwa moja ya nne ya njia karibu na mduara, kusonga kinyume chake kutoka kwa chanya x -axis. Ili kuteka angle ya 360°, tunahesabu hiyo$\frac{360°}{360°}=1$. Hivyo upande wa terminal utakuwa 1 mzunguko kamili kuzunguka mduara, kusonga kinyume chake kutoka chanya x -axis. Katika kesi hii, upande wa kwanza na upande wa terminal huingiliana. Angalia Kielelezo$\PageIndex{6}$.

Upande kwa upande grafu. Grafu upande wa kushoto ni angle ya shahada ya 90 na grafu upande wa kulia ni angle ya shahada ya 360. Upande wa terminal na upande wa awali ni lebo kwa grafu zote mbili. — Kielelezo$\PageIndex{6}$

Kwa kuwa tunafafanua angle katika nafasi ya kawaida kwa upande wake wa awali, tuna aina maalum ya angle ambayo upande wa terminal iko kwenye mhimili, angle ya quadrantal. Aina hii ya angle inaweza kuwa na kipimo cha 0°, 90°, 180°, 270° au 360°. Angalia Kielelezo$\PageIndex{7}$.

Nne upande kwa upande grafu. Grafu ya kwanza inaonyesha angle ya digrii 0. Grafu ya pili inaonyesha angle ya digrii 90. Grafu ya tatu inaonyesha angle ya digrii 180. Grafu ya nne inaonyesha angle ya digrii 270. — Kielelezo$\PageIndex{7}$: Pembe za Quadrantal ni pembe katika nafasi ya kawaida ambayo upande wa terminal iko pamoja na mhimili. Mifano huonyeshwa.

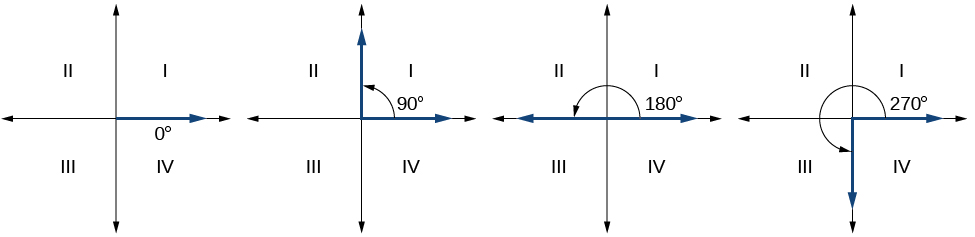
PEMBE QUADRANTAL

Pembe za quadrantali ni pembe katika nafasi ya kawaida ambayo upande wa mwisho wake upo kwenye mhimili, ikiwa ni pamoja na 0°, 90°, 180°, 270°, au 360°.

Kutokana na kipimo cha angle kwa digrii, futa angle katika nafasi ya kawaida

Eleza kipimo cha angle kama sehemu ya 360°.
Kupunguza sehemu kwa fomu rahisi.
Chora angle ambayo ina sehemu hiyo ya mduara, kuanzia kwenye chanya x -axis na kusonga kinyume chake kwa pembe nzuri na saa ya saa kwa pembe hasi.

Mfano$\PageIndex{1}$: Drawing an Angle in Standard Position Measured in Degrees

Mchoro angle ya 30° katika nafasi ya kawaida.
Panga angle ya -135° katika nafasi ya kawaida.

Suluhisho

Gawanya kipimo cha angle kwa 360°.
\[\dfrac{30°}{360°}=\dfrac{1}{12}\]

Ili kuandika upya sehemu katika sehemu inayojulikana zaidi, tunaweza kutambua kwamba

\[\dfrac{1}{12}=\dfrac{1}{3}(\frac{1}{4})\]

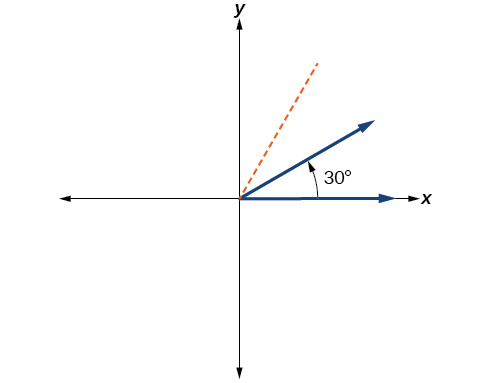
Moja ya kumi na mbili ni sawa na theluthi moja ya robo, hivyo kwa kugawa robo mzunguko katika theluthi, tunaweza mchoro line saa 30° kama katika Kielelezo$\PageIndex{8}$. $Grafu ya angle ya shahada ya 30 kwenye ndege ya xy.$
Kielelezo$\PageIndex{8}$
Gawanya kipimo cha angle kwa 360°.
\[\dfrac{−135°}{360°}=−\dfrac{3}{8}\]

Katika kesi hiyo, tunaweza kutambua kwamba

\[−\dfrac{3}{8}=−\dfrac{3}{2}(\dfrac{1}{4})\]

Hasi tatu na nane ni mara moja na nusu kwa robo, kwa hiyo tunaweka mstari kwa kusonga saa moja kwa moja robo kamili na nusu ya robo nyingine, kama ilivyo kwenye Mchoro$\PageIndex{9}$.
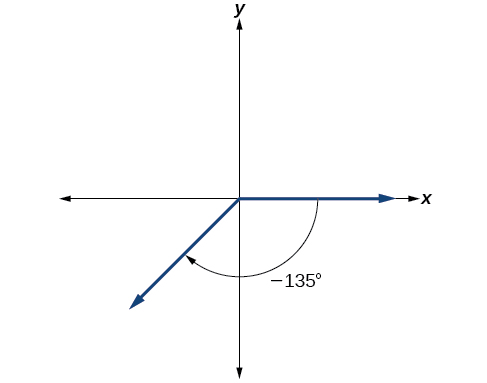
$Grafu ya angle hasi 135 shahada na mzunguko wa saa kwa upande wa terminal badala ya kinyume chake.$
Kielelezo$\PageIndex{9}$

$\PageIndex{1}$:

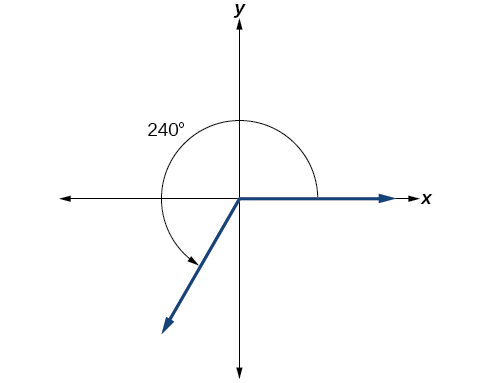
Onyesha angle ya 240° kwenye mduara katika nafasi ya kawaida.

Suluhisho

Grafu ya angle ya shahada ya 240 na mzunguko wa kinyume. — Kielelezo$\PageIndex{10}$

Kubadilisha Kati ya Degrees na Radians

Kugawanya mduara katika sehemu 360 ni chaguo la kiholela, ingawa hujenga kipimo cha kiwango cha kawaida. Tunaweza kuchagua njia zingine za kugawanya mduara. Ili kupata kitengo kingine, fikiria mchakato wa kuchora mduara. Fikiria kwamba unasimama kabla ya mduara kukamilika. Sehemu uliyovuta inajulikana kama arc. Arc inaweza kuwa sehemu ya mduara kamili, mduara kamili, au zaidi ya mzunguko kamili, unaowakilishwa na mzunguko zaidi ya moja kamili. Urefu wa arc kuzunguka mduara mzima huitwa mduara wa mduara huo.

Mzunguko wa mduara ni$C=2πr$. Ikiwa tunagawanya pande zote mbili za equation hii na$r$, tunaunda uwiano wa mzunguko kwa radius, ambayo daima$2π$ bila kujali urefu wa radius. Hivyo mduara wa mduara wowote ni$2π≈6.28$ mara urefu wa radius. Hiyo ina maana kwamba kama sisi alichukua kamba kwa muda mrefu kama Radius na kutumika kupima urefu mfululizo kuzunguka mduara, kutakuwa na nafasi ya sita full string-urefu na kidogo zaidi ya robo ya saba, kama inavyoonekana katika Kielelezo$\PageIndex{11}$.

Mfano wa mduara unaoonyesha idadi ya radians katika duara. Mduara wenye pointi juu yake na kati ya pointi mbili katika mzunguko kinyume ni namba ambayo inawakilisha ngapi radians katika arc hiyo. — Kielelezo$\PageIndex{11}$

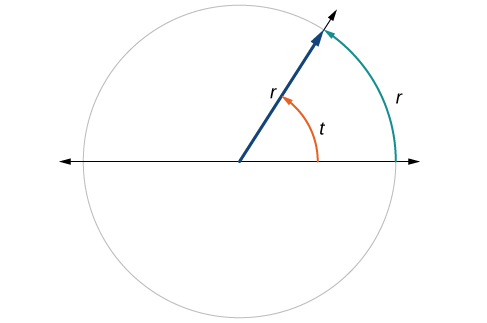
Hii inatuleta kwenye kipimo chetu kipya cha angle. Radi moja ni kipimo cha pembe ya kati ya duara inayopinga arc sawa kwa urefu kwa radius ya mduara huo. Pembe ya kati ni angle inayotengenezwa katikati ya mduara na radii mbili. Kwa sababu mzunguko wa jumla$2π$ unafanana na mara radius, mzunguko kamili wa mviringo ni$2π$ radians. Hivyo

\[\begin{align} 2π \text{ radians } & =360^∘ \\ π \text{ radians } & =\dfrac{360^∘}{2}=180^∘ \\ 1 \text{ radian } & =\dfrac{180^∘}{π}≈57.3^∘ \end{align}\]

Angalia Kielelezo$\PageIndex{12}$. Kumbuka kwamba wakati angle inavyoelezwa bila kitengo maalum, inahusu kipimo cha radian. Kwa mfano, kipimo cha angle cha 3 kinaonyesha radians 3. Kwa kweli, kipimo cha radian ni dimensionless, kwa kuwa ni quotient ya urefu (mduara) umegawanyika na urefu (radius) na vitengo vya urefu hufuta.

Mfano wa mduara na angle t, Radius r, na safu ya r. the — Kielelezo$\PageIndex{12}$:$t$ Angle inafuta kipimo cha radian moja. Kumbuka kuwa urefu wa arc iliyopigwa ni sawa na urefu wa radius ya mduara.

Kuhusiana na urefu wa Arc kwa Radius

Urefu wa arc$s$ ni urefu wa curve kando ya arc. Kama vile mzunguko kamili wa mduara daima una uwiano wa mara kwa mara na radius, urefu wa arc zinazozalishwa na angle yoyote iliyotolewa pia ina uhusiano wa mara kwa mara na radius, bila kujali urefu wa radius.

Uwiano huu, unaoitwa kipimo cha radian, ni sawa bila kujali radius ya mduara—inategemea pembe tu. Mali hii inatuwezesha kufafanua kipimo cha angle yoyote kama uwiano wa urefu wa arc s kwa radius$r$. Angalia Kielelezo$\PageIndex{13}$.

\[\begin{align} s &=rθ \\ θ &=\dfrac{s}{r} \end{align}\]

Ikiwa$ s=r$, basi$θ=\frac{r}{r}= 1 \text{ radian.}$

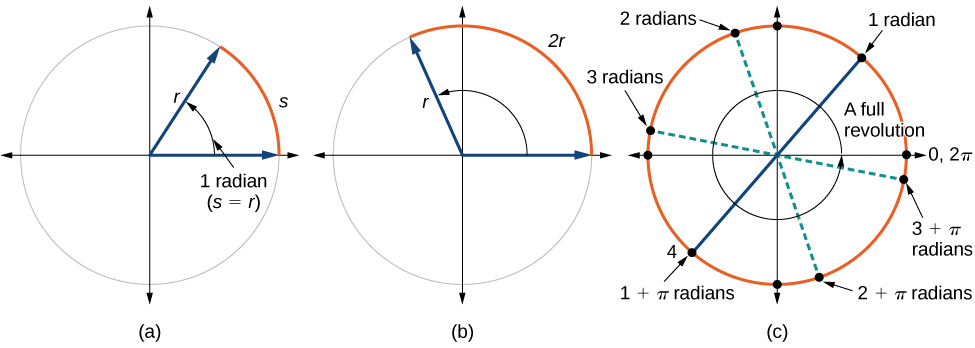
Grafu tatu za upande kwa upande wa miduara. Grafu ya kwanza ina mduara na r radius na safu s, na ulinganifu kati ya r na s. grafu ya pili inaonyesha mduara na radius r na safu ya urefu 2r. Grafu ya tatu inaonyesha duara yenye mapinduzi kamili, ikionyesha radians 6.28. — Kielelezo$\PageIndex{13}$: (a) Katika pembe ya radian 1, urefu wa arc$s$ ni sawa na radius$r.$ (b) Angle ya radians 2 ina urefu wa arc$s=2r$. (c) Mapinduzi kamili ni 2π au takriban radia 6.28.

Ili kufafanua juu ya wazo hili, fikiria miduara miwili, moja na radius 2 na nyingine yenye radius 3. Kumbuka mzunguko wa mduara ni$C=2πr$, wapi$r$ radius. Mduara mdogo basi una mduara$2π(2)=4π$ na kubwa ina mduara$2π(3)=6π$. Sasa tunapata angle ya 45° kwenye miduara miwili, kama ilivyo kwenye Mchoro$\PageIndex{14}$.

Grafu ya mduara na angle ya shahada ya 45 na lebo ya pi/4 radians. — Kielelezo$\PageIndex{14}$: Angle ya 45° ina moja ya nane ya mzunguko wa mduara, bila kujali radius.

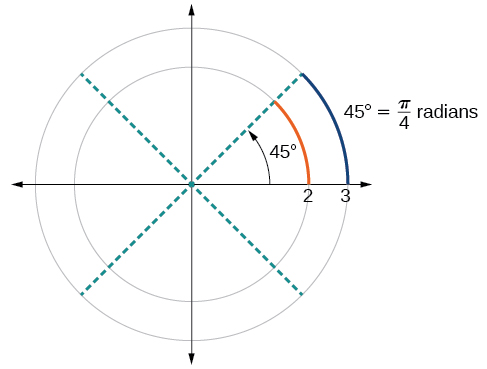
Angalia nini kinatokea ikiwa tunapata uwiano wa urefu wa arc umegawanywa na radius ya mduara.

\[\begin{align} \text{Smaller circle: } \dfrac{\frac{1}{2}π}{2} & =\dfrac{1}{4}π \\[2mm] \text{Larger circle: } \dfrac{\frac{3}{4}π}{3} & =\dfrac{1}{4}π \end{align}\]

Kwa kuwa uwiano wote ni$\frac{1}{4}π$, hatua za angle za miduara yote ni sawa, ingawa urefu wa arc na radius hutofautiana.

RADIANS

Radi moja ni kipimo cha pembe ya kati ya mduara kiasi kwamba urefu wa arc kati ya upande wa awali na upande wa terminal ni sawa na radius ya mduara. Mapinduzi kamili (360°) yanafanana na$2\pi$ radians. Nusu ya mapinduzi (180°) ni sawa na$\pi$ radians.

Kipimo cha radian cha angle ni uwiano wa urefu wa arc iliyowekwa na angle kwa radius ya mduara. Kwa maneno mengine, ikiwa$s$ ni urefu wa arc ya mduara, na$r$ ni radius ya mduara, basi angle ya kati iliyo na arc hiyo inachukua$\frac{s}{r}$ radians. Katika mduara wa radius 1, kipimo cha radian kinafanana na urefu wa arc.

Kipimo cha radian 1 kinaonekana kuwa takriban 60°. Je, hiyo ni sahihi?

Ndiyo. Ni takriban 57.3°. Kwa sababu $2π$radians ni sawa na 360°,$1$ radian sawa$\frac{360°}{2π}≈57.3°$.

Kutumia Radians

Kwa sababu kipimo cha radian ni uwiano wa urefu mbili, ni kipimo cha unitless. Kwa mfano, katika Kielelezo$\PageIndex{14}$, tuseme radius ilikuwa inchi 2 na umbali kando ya arc pia ulikuwa inchi 2. Tunapohesabu kipimo cha radian cha angle, “inchi” hufuta, na tuna matokeo bila vitengo. Kwa hiyo, si lazima kuandika studio “radians” baada ya kipimo cha radian, na tukiona angle ambayo haijaandikwa na “digrii” au alama ya shahada, tunaweza kudhani kuwa ni kipimo cha radian.

Kuzingatia kesi ya msingi zaidi, mduara wa kitengo (mduara na radius 1), tunajua kwamba mzunguko 1 unafanana na digrii 360, 360°. Pia tunaweza kufuatilia mzunguko mmoja kuzunguka mduara kwa kutafuta mduara,$C=2πr$, na kwa mduara wa kitengo Njia$C=2π.$ hizi mbili tofauti za kuzunguka mduara zinatupa njia ya kubadili kutoka digrii hadi radians.

\[\begin{array}{clll} 1 \text{rotation } & =360° & =2π & \text{radians} \\[2mm] \dfrac{1}{2} \text{rotation } & =180° & =π & \text{radians} \\[2mm] \dfrac{1}{4} \text{rotation } & =90° & =\dfrac{π}{2} & \text{radians} \end{array}\]

Kutambua Angles Maalum Kipimo katika Radians

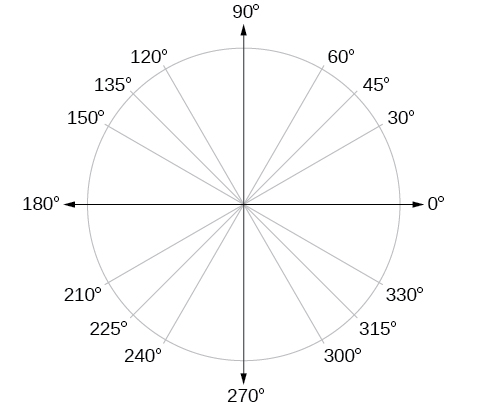
Mbali na kujua vipimo katika digrii na radians ya mapinduzi ya robo, mapinduzi ya nusu, na mapinduzi kamili, kuna pembe nyingine zilizokutana mara nyingi katika mapinduzi moja ya mduara ambayo tunapaswa kuwa na ujuzi. Ni kawaida kukutana na wingi wa digrii 30, 45, 60, na 90. Maadili haya yanaonyeshwa kwenye Kielelezo$\PageIndex{15}$. Kukumbuka pembe hizi zitakuwa muhimu sana tunapojifunza mali zinazohusiana na pembe.

Grafu ya mviringo yenye pembe za 0, 30, 45, 60, 90, 120, 135, 150, 180, 210, 225, 240, 270, 300, 315, na digrii 330. — Kielelezo$\PageIndex{15}$: Angles kawaida wamekutana kipimo katika digrii

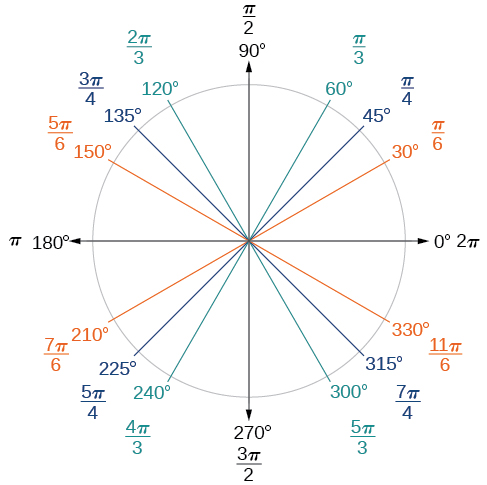
Sasa, tunaweza kuorodhesha maadili ya radian yanayofanana kwa hatua za kawaida za mduara zinazohusiana na wale waliotajwa kwenye Kielelezo$\PageIndex{15}$, ambazo zinaonyeshwa kwenye Kielelezo$\PageIndex{16}$. Hakikisha unaweza kuthibitisha kila hatua hizi.

Grafu ya mviringo yenye pembe za 0, 30, 45, 60, 90, 120, 135, 150, 180, 210, 225, 240, 270, 300, 315, na digrii 330. Grafu pia inaonyesha kiasi sawa cha radians kwa kila angle ya digrii. Kwa mfano, digrii 30 ni sawa na radians pi/6. — Kielelezo$\PageIndex{16}$: Angles kawaida wamekutana kipimo katika radians

Mfano$\PageIndex{2}$: Finding a Radian Measure

Pata kipimo cha radian cha theluthi moja ya mzunguko kamili.

Suluhisho

Kwa mduara wowote, urefu wa arc pamoja na mzunguko huo utakuwa theluthi moja ya mzunguko. Tunajua kwamba

\[1 \text{ rotation}=2πr\]

Hivyo,

\[\begin{align}s &= \dfrac{1}{3}(2πr) \\[2mm] &=\dfrac{2πr}{3} \end{align}\]

Kipimo cha radian kitakuwa urefu wa arc umegawanyika na radius.

\[\begin{align} \text{radian measure} & = \dfrac{\frac{2πr}{3}}{r} \\[2mm] &= \dfrac{2πr}{3r} \\[2mm] & = \dfrac{2π}{3} \end{align}\]

$\PageIndex{2}$

Pata kipimo cha radian cha robo tatu za mzunguko kamili.

Suluhisho

\[\dfrac{3π}{2}\]

Kubadilisha kati ya Radians na Degrees

Kwa sababu digrii na radians zote mbili hupima pembe, tunahitaji kuwa na uwezo wa kubadilisha kati yao. Tunaweza kufanya hivyo kwa urahisi kwa kutumia uwiano.

\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]

Uwiano huu unaonyesha kwamba kipimo cha angle$θ$ katika digrii kilichogawanywa na 180 kinalingana na kipimo cha angle$θ$ katika radians iliyogawanywa na$π.$ Au, iliyosemwa kwa njia nyingine, digrii ni 180 kama radians ni kwa$π$.

\[\dfrac{\text{Degrees}}{180}=\dfrac{Radians}{π} \]

KUBADILISHA KATI YA RADIANS NA DIG

Ili kubadilisha kati ya digrii na radians, tumia uwiano

\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]

Mfano$\PageIndex{3}$: Converting Radians to Degrees

Geuza kila kipimo cha radian kwa digrii.

$\frac{π}{6}$
3

Suluhisho

Kwa sababu tunapewa radians na tunataka digrii, tunapaswa kuanzisha uwiano na kutatua.

Tunatumia uwiano, kubadilisha habari iliyotolewa.
\[\begin{align}\dfrac{θ}{180} &=\dfrac{θ^R}{π} \\[2mm] \dfrac{θ}{180} & =\dfrac{\frac{π}{6}}{π} \\ θ & =\dfrac{180}{6} \\ θ & =30^∘ \end{align}\]
Tunatumia uwiano, kubadilisha habari iliyotolewa.
\[\begin{align}\dfrac{θ}{180} &= \dfrac{θ^R}{π} \\ \dfrac{θ}{180} &=\dfrac{3}{π} \\ θ &= \dfrac{3(180)}{π} \\ θ & ≈172^∘ \end{align}\]

$\PageIndex{3}$

Geuza$−\frac{3π}{4}$ radians kwa digrii.

Suluhisho

-135°

Mfano$\PageIndex{4}$: Converting Degrees to Radians

Badilisha$15$ digrii kwa radians.

Suluhisho

Katika mfano huu, tunaanza na digrii na tunataka radians, kwa hiyo tunaanzisha tena uwiano na kuitatua, lakini tunabadilisha habari iliyotolewa katika sehemu tofauti ya uwiano.

\[\begin{align}\dfrac{θ}{180} &= \dfrac{θ^R}{π} \\ \dfrac{15}{180} &=\dfrac{θ^R}{π} \\ \dfrac{15π}{180} & =θ^R \\ \dfrac{π}{12} & =θ^R \end{align}\]

Uchambuzi

Njia nyingine ya kufikiri juu ya tatizo hili ni kwa kukumbuka hilo$30^∘=\frac{π}{6}$. Kwa sababu$15^∘=\frac{1}{2}(30^∘)$,, tunaweza kupata kwamba$\frac{1}{2}(\frac{π}{6})$ ni$\frac{π}{12}$.

$\PageIndex{4}$

Geuza 126° kwa radiani.

Suluhisho

$\frac{7π}{10}$

Kupata pembe za Coterminal

Kubadili kati ya digrii na radians kunaweza kufanya kazi na pembe rahisi katika baadhi ya programu. Kwa programu nyingine, tunaweza kuhitaji aina nyingine ya uongofu. Pembe hasi na pembe kubwa kuliko mapinduzi kamili ni Awkward zaidi kufanya kazi na kuliko zile katika upeo wa 0° hadi 360°, au 0 kwa$2π$. Ingekuwa rahisi kuchukua nafasi ya pembe hizo za nje na angle inayofanana ndani ya mapinduzi moja.

Inawezekana kwa angle zaidi ya moja kuwa na upande huo wa terminal. Angalia Kielelezo$\PageIndex{17}$. Pembe ya 140° ni angle chanya, kupimwa kinyume chake. Pembe ya -220° ni angle hasi, inayopimwa mwendo wa saa. Lakini pembe zote mbili zina upande wa terminal sawa. Ikiwa pembe mbili katika nafasi ya kawaida zina upande huo wa terminal, ni pembe za coterminal. Kila angle kubwa kuliko 360° au chini ya 0° ni coterminal yenye angle kati ya 0° na 360°, na mara nyingi ni rahisi zaidi kupata angle ya coterminal ndani ya upeo wa 0° hadi 360° kuliko kufanya kazi kwa pembe iliyo nje ya upeo huo.

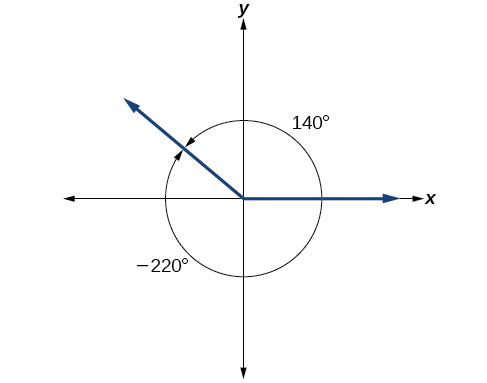
Grafu inayoonyesha ulinganifu kati ya angle ya shahada 140 na angle hasi 220 shahada. Angle ya digrii 140 ni mzunguko wa kinyume ambapo angle ya shahada 220 ni mzunguko wa saa moja kwa moja. — Kielelezo$\PageIndex{17}$: Angle ya 140° na angle ya -220° ni pembe za coterminal.

Pembe yoyote ina pembe nyingi za coterminal kwa sababu kila wakati tunaongeza 360° kwenye angle-au toa 360° kutoka humo - thamani inayosababisha ina upande wa mwisho katika eneo moja. Kwa mfano, 100° na 460° ni coterminal kwa sababu hii, kama ilivyo -260°. Kutambua kwamba angle yoyote ina pembe nyingi za coterminal inaelezea sura inayojirudia katika grafu za kazi za trigonometric.

Angle ya kumbukumbu ya angle ni kipimo cha angle ndogo, chanya, papo hapo$t$ iliyoundwa na upande wa mwisho wa angle$t$ na mhimili usio na usawa. Hivyo pembe za kumbukumbu nzuri zina pande za mwisho ambazo ziko katika quadrant ya kwanza na zinaweza kutumika kama mifano ya pembe katika quadrants nyingine. Angalia Kielelezo$\PageIndex{18}$ kwa mifano ya pembe za kumbukumbu kwa pembe katika quadrants tofauti.

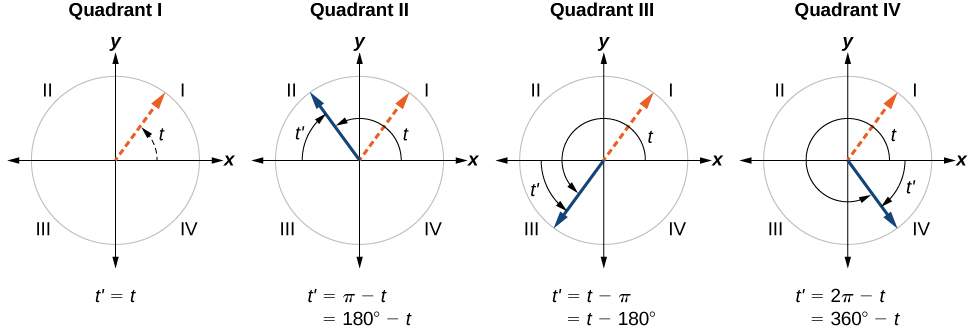
Grafu nne za upande kwa upande. Grafu ya kwanza inaonyesha angle ya t katika quadrant 1 katika nafasi yake ya kawaida. Grafu ya pili inaonyesha angle ya t katika roboduara 2 kutokana na mzunguko wa pi bala t. grafu ya tatu inaonyesha angle ya t katika roboduara 3 kutokana na mzunguko wa t minus pi. Grafu ya nne inaonyesha angle ya t katika quadrant 4 kutokana na mzunguko wa pi mbili minus t. — Kielelezo$\PageIndex{18}$

COTERMINAL NA KUMBUKUMBU

Pembe za Coterminal ni pembe mbili katika nafasi ya kawaida ambayo ina upande huo wa terminal.
Angle ya kumbukumbu ya angle ni ukubwa wa angle ndogo zaidi$t′$, iliyoundwa na upande wa mwisho wa angle$t$ na mhimili usio na usawa.

Kutokana na angle kubwa kuliko 360°, tafuta angle ya coterminal kati ya 0° na 360°

Ondoa 360° kutoka pembe iliyotolewa.
Kama matokeo bado ni makubwa kuliko 360°, toa 360° tena mpaka matokeo yawe kati ya 0° na 360°.
Pembe inayosababisha ni coterminal na angle ya awali.

Mfano$\PageIndex{5}$: Finding an Angle Coterminal with an Angle of Measure Greater Than 360°

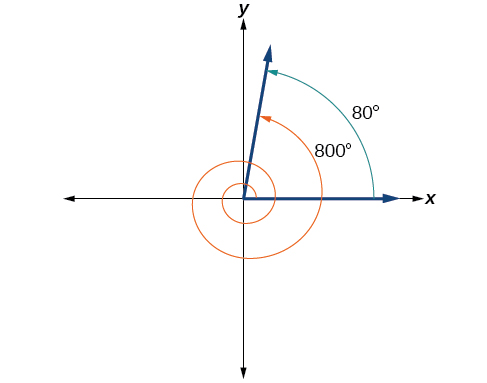
Kupata angalau chanya angle yaani coterminal na angle kupima 800°, ambapo$0°≤θ<360°$.

Suluhisho

Pembe yenye kipimo 800° ni koterminal yenye angle yenye kipimo 800 ÷ 360 = 440°, lakini 440° bado ni kubwa kuliko 360°, hivyo tunaondoa 360° tena ili tupate angle nyingine ya coterminal: 440 ÷ 360 = 80°.

Pembe$θ=80°$ ni coterminal yenye 800°. Ili kuiweka njia nyingine, 800° sawa na 80° pamoja na mzunguko kamili mbili, kama inavyoonekana katika Kielelezo$\PageIndex{19}$.

Grafu inayoonyesha ulinganifu kati ya angle ya digrii 80 na angle ya digrii 800 ambapo angle ya shahada 800 ni mzunguko kamili mbili na ina nafasi sawa ya upande wa terminal kama shahada 80. — Kielelezo$\PageIndex{19}$

$\PageIndex{5}$

Kupata angle$α$ ambayo ni coterminal na angle kupima 870°, ambapo$0°≤α<360°$.

Suluhisho

$α=150°$

Kutokana na angle yenye kipimo cha chini ya 0°, tafuta angle ya coterminal yenye kipimo kati ya 0° na 360°.

Ongeza 360° kwenye angle iliyotolewa.
Kama matokeo bado ni chini ya 0°, ongeza 360° tena mpaka matokeo yawe kati ya 0° na 360°.
Pembe inayosababisha ni coterminal na angle ya awali.

Mfano$\PageIndex{6}$: Finding an Angle Coterminal with an Angle Measuring Less Than 0°

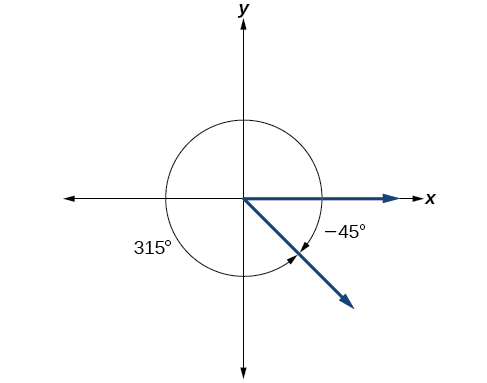
Onyesha angle kwa kipimo -45° kwenye mduara na pata angle ya koterminal chanya α kama kwamba 0° ≤ α <360°.

Suluhisho

Kwa kuwa 45° ni nusu ya 90°, tunaweza kuanza kwenye mhimili mzuri wa usawa na kupima nusu ya saa ya angle ya 90°.

Kwa sababu tunaweza kupata pembe za coterminal kwa kuongeza au kuondoa mzunguko kamili wa 360°, tunaweza kupata angle nzuri ya coterminal hapa kwa kuongeza 360°:

\[−45°+360°=315°\]

Tunaweza kisha kuonyesha angle kwenye mduara, kama katika Kielelezo$\PageIndex{20}$.

Grafu inayoonyesha ulinganifu wa angle ya shahada ya 315 na angle hasi ya digrii 45. Angle ya shahada ya 315 iko kwenye mzunguko wa kinyume wakati angle ya shahada ya 45 iko kwenye mzunguko wa saa. — Kielelezo$\PageIndex{20}$

$\PageIndex{6}$

Pata angle β yaani coterminal yenye angle ya kupima -300° kama hiyo$0°≤β<360°$.

Suluhisho

$β=60°$

Kutafuta pembe za Coterminal Kupimwa kwa Radians

Tunaweza kupata pembe za coterminal kupimwa kwa radians kwa njia sawa sana kama tulivyoyaona kwa kutumia digrii. Katika matukio hayo yote, tunapata pembe za coterminal kwa kuongeza au kuondoa mzunguko mmoja au zaidi kamili.

Kutokana na angle kubwa kuliko$2\pi$, find a coterminal angle between 0 and $2\pi$.

Ondoa$2π$ kutoka angle iliyotolewa.
Ikiwa matokeo bado ni makubwa zaidi kuliko$2π$, toa$2π$ tena mpaka matokeo yapo kati$0$ na$2π$.
Pembe inayosababisha ni coterminal na angle ya awali.

Mfano$\PageIndex{7}$: Finding Coterminal Angles Using Radians

Kupata angle$β$ kwamba ni coterminal na$\frac{19π}{4}$, ambapo$0≤β<2π.$

Suluhisho

Tunapofanya kazi kwa digrii, tulipata pembe za coterminal kwa kuongeza au kuondoa digrii 360, mzunguko kamili. Vivyo hivyo, katika radians, tunaweza kupata pembe za coterminal kwa kuongeza au kuondoa mzunguko kamili wa$2π$ radians:

\[\begin{align} \dfrac{19π}{4}−2π & =\dfrac{19π}{4}−\dfrac{8π}{4} \\ &=\dfrac{11π}{4} \end{align}\]

Pembe$\frac{11π}{4}$ ni coterminal, lakini si chini ya$2π$, hivyo tunaondoa mzunguko mwingine:

\[\begin{align} \dfrac{11π}{4}−2π &= \dfrac{11π}{4}−\dfrac{8π}{4} \\ &= \dfrac{3π}{4} \end{align}\]

Pembe$\frac{3π}{4}$ ni coterminal na$\frac{19π}{4}$, kama inavyoonekana katika Kielelezo$\PageIndex{21}$.

Grafu inayoonyesha mduara na ulinganifu kati ya pembe za radians 3pi/4 na radians 19pi/4. 19pi/4 hufanya mzunguko wawili kamili kabla ya kuishia katika sehemu moja kama 3pi/4. — Kielelezo$\PageIndex{21}$

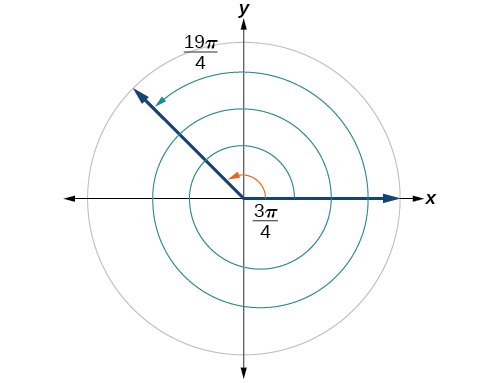
$\PageIndex{7}$

Kupata angle ya kipimo$θ$ kwamba ni coterminal na angle ya kipimo$−\frac{17π}{6}$ ambapo$0≤θ<2π.$

Suluhisho

$\frac{7π}{6}$

Kuamua Urefu wa Arc

Kumbuka kwamba kipimo cha radian$θ$ cha angle kilifafanuliwa kama uwiano wa urefu wa arc$s$ ya mviringo kwa radius$r$ ya mduara,$θ=\frac{s}{r}$. Kutokana na uhusiano huu, tunaweza kupata urefu wa arc kando ya mduara, kutokana na angle.

UREFU WA ARC KWENYE MDUARA

Katika mduara wa radius r, urefu wa arc$s$ unafungwa na angle na kipimo$θ$ katika radians, inavyoonekana katika Kielelezo$\PageIndex{22}$, ni

\[s=rθ\]

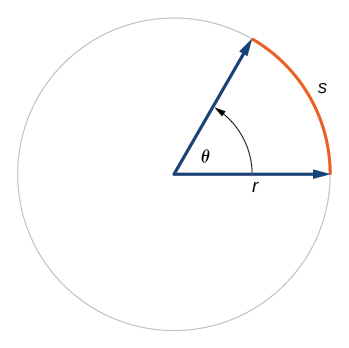
Mfano wa mduara na theta ya angle, radius r, na arc na urefu s. — Kielelezo$\PageIndex{22}$

Kutokana na mduara wa radius$r,$ calculate the length $s$ of the arc subtended by a given angle of measure $θ$.

Ikiwa ni lazima, kubadilisha$θ$ kwa radians.
Kuzidisha$r$ radius kwa kipimo radian ya$θ:s=rθ$.

Mfano$\PageIndex{8}$: Finding the Length of an Arc

Tuseme obiti ya Mercury karibu na jua ni mduara kamilifu. Mercury ni takriban maili milioni 36 kutoka jua.

Katika siku moja ya Dunia, Mercury inakamilisha 0.0114 ya mapinduzi yake yote. Je, ni maili ngapi husafiri kwa siku moja?
Tumia jibu lako kutoka sehemu (a) kuamua kipimo cha radian kwa mwendo wa Mercury katika siku moja ya Dunia.

Suluhisho

Hebu tuanze kwa kutafuta mzunguko wa obiti ya Mercury.
\[\begin{align} C &=2πr \\ &=2π(\text{36 million miles}) \\ &≈226 \text{ million miles} \end{align}\]

Kwa kuwa Mercury inakamilisha 0.0114 ya mapinduzi yake yote katika siku moja ya Dunia, sasa tunaweza kupata umbali uliosafiri:

\[(0.0114)226 \text{ million miles} = 2.58 \text{ million miles}\]
Sasa, tunabadilisha kuwa radians:
\[\begin{align} \text{radian} & = \dfrac{\text{arc length}}{\text{radius}} \\ &= \dfrac{2.58 \text{ million miles}}{36 \text{ million miles}} \\ & =0.0717 \end{align} \]

$\PageIndex{8}$

Pata urefu wa arc kwenye mduara wa vitengo vya radius 10 vilivyowekwa na angle ya 215°.

Suluhisho

\[\dfrac{215π}{18}=37.525 \text{ units} \]

Kutafuta Eneo la Sekta ya Mzunguko

Mbali na urefu wa arc, tunaweza pia kutumia pembe ili kupata eneo la sekta ya mduara. Sekta ni kanda ya mduara iliyofungwa na radii mbili na arc iliyokataliwa, kama kipande cha pizza au pai. Kumbuka kwamba eneo la mduara na radius$r$ linaweza kupatikana kwa kutumia formula$A=πr^2$. Ikiwa radii mbili zinaunda angle ya$θ$, kupimwa kwa radians, basi$\frac{θ}{2π}$ ni uwiano wa kipimo cha angle kwa kipimo cha mzunguko kamili na pia ni, kwa hiyo, uwiano wa eneo la sekta kwa eneo la mduara. Hivyo, eneo la sekta ni sehemu$\frac{θ}{2π}$ inayoongezeka kwa eneo lote. (Daima kumbuka kwamba formula hii inatumika tu ikiwa$θ$ iko katika radians.)

\[\begin{align} \text{Area of sector} & =(\dfrac{θ}{2π})πr^2 \\ &=\dfrac{θπr^2}{2π} \\ & =\dfrac{1}{2}θr^2 \end{align}\]

ENEO LA SEKTA

Eneo la sekta ya mduara na radius$r$ iliyowekwa na angle$θ$, kipimo katika radians, ni

\[A=\dfrac{1}{2}θr^2\]

Angalia Kielelezo$\PageIndex{23}$.

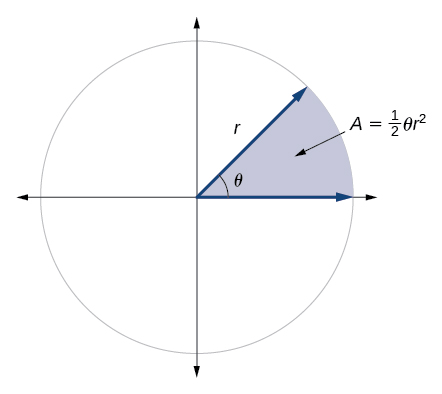
Grafu kuonyesha mduara na angle theta na Radius r, na eneo la kipande cha mduara kuundwa kwa upande wa awali na upande terminal ya angle. kipande ni kinachoitwa: A sawa mara nusu moja theta mara r squared. — Kielelezo$\PageIndex{23}$: Eneo la sekta hiyo ni sawa na nusu ya mraba wa radius mara angle ya kati iliyopimwa kwa radians.

Kutokana na mduara wa radius$r,$ find the area of a sector defined by a given angle $θ.$

Ikiwa ni lazima, kubadilisha$θ$ kwa radians.
Panua nusu ya kipimo cha radian$θ$ cha mraba wa radius$r: A=\frac{1}{2}θr^2.$

Mfano$\PageIndex{9}$: Finding the Area of a Sector

Sprinkler moja kwa moja lawn dawa umbali wa miguu 20 wakati kupokezana digrii 30, kama inavyoonekana katika Kielelezo$\PageIndex{24}$. Ni eneo gani la sekta ya nyasi maji ya sprinkler?

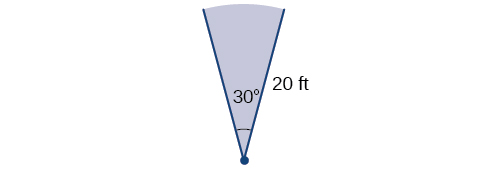
Mfano wa angle ya shahada 30 na upande wa mwisho na wa awali na urefu wa miguu 20. — Kielelezo$\PageIndex{24}$: Sprinkler hunyunyizia futi 20 ndani ya safu ya 30°.

Suluhisho

Kwanza, tunahitaji kubadilisha kipimo cha angle ndani ya radians. Kwa sababu digrii 30 ni moja ya pembe zetu maalum, tayari tunajua kipimo sawa cha radian, lakini tunaweza pia kubadilisha:

\[\begin{align} \text{30 degrees} &=30⋅\frac{π}{180} \\ &=\frac{π}{6} \text{ radians} \end{align}\]

Eneo la sekta hiyo ni basi

\[\begin{align} \text{Area} &= \dfrac{1}{2}(\dfrac{π}{6})(20)^2 \\ & ≈104.72 \end{align}\]

Hivyo eneo hilo ni karibu$\mathrm{104.72 \; ft^2}$.

$\PageIndex{9}$

Katika umwagiliaji wa kati wa pivot, bomba kubwa la umwagiliaji kwenye magurudumu huzunguka karibu na kituo cha katikati. Mkulima ana mfumo wa egemeo kuu wenye radius ya mita 400. Ikiwa vikwazo vya maji vinamruhusu kumwagilia mita za mraba 150,000 kwa siku, ni angani gani anapaswa kuweka mfumo wa kufunika? Andika jibu kwa kipimo cha radian kwa sehemu mbili za decimal.

Suluhisho

1.88

Tumia Kasi ya Linear na Angular Kuelezea Mwendo kwenye Njia ya Mviringo

Mbali na kutafuta eneo la sekta, tunaweza kutumia pembe kuelezea kasi ya kitu kinachohamia. Kitu kinachosafiri katika njia ya mviringo kina aina mbili za kasi. Kasi ya mstari ni kasi kwenye njia moja kwa moja na inaweza kuamua na umbali unaoendelea pamoja (uhamisho wake) kwa muda uliopatikana. Kwa mfano, ikiwa gurudumu yenye radius inchi 5 huzunguka mara moja kwa pili, hatua kwenye makali ya gurudumu husababisha umbali sawa na mduara, au inchi 10π, kila sekunde. Hivyo kasi ya mstari wa uhakika$10π$ iko. /s. equation kwa kasi linear ni kama ifuatavyo ambapo$v$ ni linear kasi,$s$ ni makazi yao, na$t$ ni wakati.

\[v=\dfrac{s}{t}\]

Matokeo ya kasi ya angular kutoka mwendo wa mviringo na inaweza kuamua na angle kwa njia ambayo hatua inazunguka kwa muda uliopewa. Kwa maneno mengine, kasi ya angular ni mzunguko wa angular kwa wakati wa kitengo. Kwa hiyo, kwa mfano, ikiwa gear inafanya mzunguko kamili kila sekunde 4, tunaweza kuhesabu kasi yake ya angular kama digrii$\frac{360 \text{ degrees}}{4 \text{ seconds}}= $ 90 kwa sekunde. Kasi ya angular inaweza kutolewa kwa radians kwa pili, mzunguko kwa dakika, au digrii kwa saa kwa mfano. equation kwa kasi angular ni kama ifuatavyo, ambapo$ω$ (kusoma kama omega)$θ$ ni angular kasi, ni angle kupita, na$t$ ni wakati.

\[ω=\dfrac{θ}{t}\]

Kuchanganya ufafanuzi wa kasi ya angular na usawa wa urefu wa arc$s=rθ$,, tunaweza kupata uhusiano kati ya kasi ya angular na ya mstari. angular kasi equation inaweza kutatuliwa kwa$θ$, kutoa$θ=ωt.$ Kubadilisha hii katika safu urefu equation anatoa:

\[\begin{align}s &=rθ \\ &=rωt \end{align}\]

Kubadilisha hii katika equation ya kasi ya mstari inatoa:

\[\begin{align} v & = \dfrac{s}{t} &=\dfrac{rωt}{t} &=rω \end{align}\]

KASI YA ANGULAR NA YA KAWAIDA

Kama hatua hatua pamoja mduara wa Radius kasi$r,$ yake angular$ω$,, ni mzunguko angular$θ$ kwa wakati kitengo,$t$.

\[ω=\dfrac{θ}{t}\]

Kasi ya mstari. $v$, ya uhakika inaweza kupatikana kama umbali uliosafiri, urefu wa arc$s$, kwa wakati wa kitengo,$t.$

\[v=\frac{s}{t}\]

Wakati kasi ya angular inapimwa kwa radians kwa wakati wa kitengo, kasi ya mstari na kasi ya angular ni kuhusiana na equation

\[v=rω\]

Equation hii inasema kuwa kasi ya angular katika radians$ω$, inayowakilisha kiasi cha mzunguko kinachotokea katika kitengo cha wakati, inaweza kuzidishwa na radius$r$ kuhesabu urefu wa jumla wa safu uliosafiri katika kitengo cha muda, ambayo ni ufafanuzi wa kasi ya mstari.

Kutokana na kiasi cha mzunguko wa angle na wakati uliopita, tumia kasi ya angular

Ikiwa ni lazima, kubadilisha kipimo cha angle kwa radians.
Gawanya angle katika radians kwa idadi ya vitengo vya wakati uliopita:$ω=\frac{θ}{t}.$
Kasi ya kusababisha itakuwa katika radians kwa kitengo cha wakati.

Mfano$\PageIndex{10}$: Finding Angular Speed

Gurudumu la maji, lililoonyeshwa kwenye Kielelezo$\PageIndex{25}$, linakamilisha mzunguko 1 kila sekunde 5. Pata kasi ya angular katika radians kwa pili.

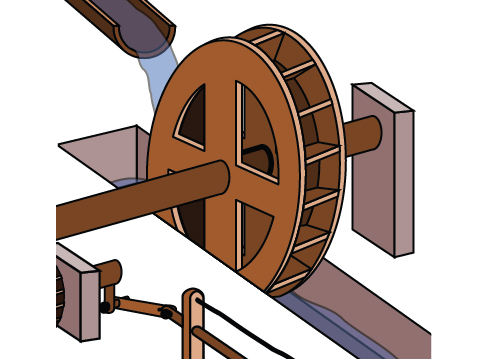
Mfano wa gurudumu la maji. — Kielelezo$\PageIndex{25}$

Suluhisho

Gurudumu hukamilisha mzunguko 1, au hupita kupitia pembe ya$2π$ radians katika sekunde 5, hivyo kasi ya angular itakuwa$ω=\frac{2π}{5}≈1.257$ radians kwa sekunde.

$\PageIndex{10}$

Rekodi ya zamani ya vinyl inachezwa kwenye turntable inayozunguka saa moja kwa moja kwa kiwango cha mzunguko wa 45 kwa dakika. Pata kasi ya angular katika radians kwa pili.

Suluhisho

$−\frac{3π}{2}$rad/s

Kutokana na radius ya mduara, angle ya mzunguko, na urefu wa muda uliopita, tambua kasi ya mstari

Badilisha mzunguko wa jumla kwa radians ikiwa ni lazima.
Gawanya mzunguko wa jumla katika radians kwa muda uliopita ili kupata kasi ya angular: tumia$ω=\frac{θ}{t}$.
Panua kasi ya angular kwa urefu wa radius ili kupata kasi ya mstari, iliyoelezwa kwa mujibu wa kitengo cha urefu kilichotumiwa kwa radius na kitengo cha muda kilichotumiwa kwa muda uliopita: tumia$v=rω$.

Mfano$\PageIndex{11}$: Finding a Linear Speed

Baiskeli ina magurudumu 28 inchi kipenyo. Tachometer huamua magurudumu yanazunguka saa 180 RPM (mapinduzi kwa dakika). Find kasi ya baiskeli ni kusafiri barabarani.

Suluhisho

Hapa, tuna kasi ya angular na tunahitaji kupata kasi inayofanana ya mstari, kwa kuwa kasi ya mstari wa nje ya matairi ni kasi ambayo baiskeli husafiri barabarani.

Tunaanza kwa kubadili kutoka mzunguko kwa dakika kwa radians kwa dakika. Inaweza kuwa na manufaa kwa kutumia vitengo kufanya uongofu huu:

\[\mathrm{180 \dfrac{\cancel{rotations}}{minute}⋅\dfrac{2π \; radians}{\cancel{rotation}}=360π\dfrac{radians}{minute}}\]

Kutumia formula kutoka juu pamoja na radius ya magurudumu, tunaweza kupata kasi ya mstari:

\[\begin{align} v & =(14 \text{ inches})(360π \dfrac{\text{radians}}{\text{minute}}) \\ &=5040π \dfrac{\text{inches}}{\text{minute}} \end{align}\]

Kumbuka kwamba radians ni kipimo cha unitless, hivyo si lazima kuwaingiza. Kipimo cha unitless, hivyo si lazima kuziingiza.

Hatimaye, tunaweza kutaka kubadilisha kasi hii linear katika kipimo zaidi ukoo, kama maili kwa saa.

\[\mathrm{5040π\dfrac{\cancel{inches}}{\cancel{minute}}⋅\dfrac{1 \; \cancel{ feet}}{12 \; \cancel{ inches}}⋅\dfrac{1 \; \cancel{ mile}}{5280 \cancel{ feet}}⋅\dfrac{60 \cancel{ minutes}}{1 \; hour}≈14.99 \; miles \; per \; hour \; (mph)}\]

$alt$ $\PageIndex{11}$

Satellite inazunguka kuzunguka Dunia kwa radians 0.25 kwa saa kwenye kimo cha kilomita 242 juu ya Dunia. Ikiwa radius ya Dunia ni kilomita 6378, pata kasi ya mstari wa satellite katika kilomita kwa saa.

Suluhisho

Kilomita 1655 kwa saa

vyombo vya habari

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na pembe, urefu wa arc, na maeneo ya sekta.

Mlinganyo muhimu

urefu wa arc	$s=rθ$
area of a sector	$A=\frac{1}{2}θr^2$
angular speed	$ω=\frac{θ}{t}$
linear speed	$v=\frac{s}{t}$
linear speed related to angular speed	$v=rω$

Key Concepts

An angle is formed from the union of two rays, by keeping the initial side fixed and rotating the terminal side. The amount of rotation determines the measure of the angle.
An angle is in standard position if its vertex is at the origin and its initial side lies along the positive x-axis. A positive angle is measured counterclockwise from the initial side and a negative angle is measured clockwise.
To draw an angle in standard position, draw the initial side along the positive x-axis and then place the terminal side according to the fraction of a full rotation the angle represents. See Example.
In addition to degrees, the measure of an angle can be described in radians. See Example.
To convert between degrees and radians, use the proportion $\frac{θ}{180}=\frac{θ^R}{π}$. See Example and Example.
Two angles that have the same terminal side are called coterminal angles.
We can find coterminal angles by adding or subtracting 360° or $2π$. See Example and Example.
Coterminal angles can be found using radians just as they are for degrees. See Example.
The length of a circular arc is a fraction of the circumference of the entire circle. See Example.
The area of sector is a fraction of the area of the entire circle. See Example.
An object moving in a circular path has both linear and angular speed.
The angular speed of an object traveling in a circular path is the measure of the angle through which it turns in a unit of time. See Example.
The linear speed of an object traveling along a circular path is the distance it travels in a unit of time. See Example.

Glossary

angle: the union of two rays having a common endpoint

angular speed: the angle through which a rotating object travels in a unit of time

arc length: the length of the curve formed by an arc

area of a sector: area of a portion of a circle bordered by two radii and the intercepted arc; the fraction $\frac{θ}{2π}$ multiplied by the area of the entire circle

coterminal angles: description of positive and negative angles in standard position sharing the same terminal side

degree: a unit of measure describing the size of an angle as one-360th of a full revolution of a circle

initial side: the side of an angle from which rotation begins

linear speed: the distance along a straight path a rotating object travels in a unit of time; determined by the arc length

measure of an angle: the amount of rotation from the initial side to the terminal side

negative angle: description of an angle measured clockwise from the positive x-axis

positive angle: description of an angle measured counterclockwise from the positive x-axis

quadrantal angle: an angle whose terminal side lies on an axis

radian measure: the ratio of the arc length formed by an angle divided by the radius of the circle

radian: the measure of a central angle of a circle that intercepts an arc equal in length to the radius of that circle

ray: one point on a line and all points extending in one direction from that point; one side of an angle

reference angle: the measure of the acute angle formed by the terminal side of the angle and the horizontal axis

standard position: the position of an angle having the vertex at the origin and the initial side along the positive x-axis

terminal side: the side of an angle at which rotation ends

vertex: the common endpoint of two rays that form an angle

\(θ\)	\(φ \text{ or }ϕ\)	\(α\)	\(β\)	\(γ\)
theta	phi	alpha	beta	gamma

urefu wa arc	\(s=rθ\)
area of a sector	\(A=\frac{1}{2}θr^2\)
angular speed	\(ω=\frac{θ}{t}\)
linear speed	\(v=\frac{s}{t}\)
linear speed related to angular speed	\(v=rω\)