7.6: Mfano na Ulinganifu wa Trigonometric

Last updated
Save as PDF

Page ID: 181492

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Tuseme sisi charted wastani joto kila siku katika New York City katika kipindi cha mwaka mmoja. Tunataka kutarajia kupata joto chini kabisa katika Januari na Februari na ya juu katika Julai na Agosti. Mzunguko huu unaojulikana unarudia mwaka baada ya mwaka, na kama tungekuwa na kupanua grafu zaidi ya miaka mingi, ingekuwa inafanana na kazi ya mara kwa mara.

Kielelezo$\PageIndex{1}$: Mikono ya saa ni mara kwa mara: hurudia nafasi kila masaa kumi na mbili. (mikopo: “zoutedrop” /Flickr)

Matukio mengine mengi ya asili pia ni mara kwa mara. Kwa mfano, awamu za mwezi zina kipindi cha takriban siku 28, na ndege wanajua kuruka kusini takriban wakati uleule kila mwaka. Hivyo jinsi gani tunaweza mfano equation kutafakari tabia ya mara kwa mara? Kwanza, tunapaswa kukusanya na kurekodi data. Kisha tunapata kazi inayofanana na muundo uliozingatiwa. Hatimaye, tunafanya mabadiliko muhimu kwa kazi ili kupata mfano ambao unategemea. Katika sehemu hii, tutaangalia zaidi aina maalum za tabia ya mara kwa mara na usawa wa mfano ili kufaa data.

Kuamua Amplitude na Kipindi cha Kazi ya Sinusoidal

Mwendo wowote unaojirudia yenyewe katika kipindi cha muda uliowekwa unachukuliwa kuwa mwendo wa mara kwa mara na unaweza kuonyeshwa na kazi ya sinusoidal. Ukubwa wa kazi ya sinusoidal ni umbali kutoka midline hadi thamani ya juu, au kutoka midline hadi thamani ya chini. Midline ni thamani ya wastani. Kazi za sinusoidal zinasonga juu na chini ya midline, ni mara kwa mara, na kurudia maadili katika mzunguko uliowekwa. Kumbuka kutoka kwa Grafu za Kazi za Sine na Cosine kwamba kipindi cha kazi ya sine na kazi ya cosine ni$2π$. Kwa maneno mengine, kwa thamani yoyote ya$x$,

\[ \sin(x±2πk)=\sin x \; \text{and} \; \cos(x±2πk)=\cos x \]

$k$wapi integer.

AINA YA KAWAIDA YA EQUATIONS YA SINUSOIDAL

Aina ya jumla ya equation ya sinusoidal hutolewa kama

\[y=A \sin(Bt−C)+D\]

\[ y=A \cos(Bt−C)+D\]

ambapo$\text{amplitude}=|A|,B$ ni kuhusiana na kipindi kama kwamba$\text{period}=\frac{2π}{B},C$ ni awamu kuhama kama kwamba$\frac{C}{B}$ inaashiria mabadiliko ya usawa, na$D$ inawakilisha mabadiliko wima kutoka grafu ya mzazi grafu.

Kumbuka kuwa mifano wakati mwingine imeandikwa kama

\[y=a \sin (ω t±C)+D\]

\[y=a \cos(ω t±C)+D,\]

na kipindi kwamba ni kutolewa kama$\frac{2π}{ω}$.

Tofauti kati ya sine na grafu za cosine ni kwamba grafu ya sine huanza na thamani ya wastani ya kazi na grafu ya cosine huanza na thamani ya juu au ya chini ya kazi.

Mfano$\PageIndex{1}$: Showing How the Properties of a Trigonometric Function Can Transform a Graph

Onyesha mabadiliko ya grafu ya$y=\sin x$ ndani ya grafu ya$y=2 \sin(4x−\frac{π}{2})+2$.

Suluhisho

Fikiria mfululizo wa grafu katika Kielelezo$\PageIndex{1}$ na njia ya kila mabadiliko ya equation mabadiliko ya picha.

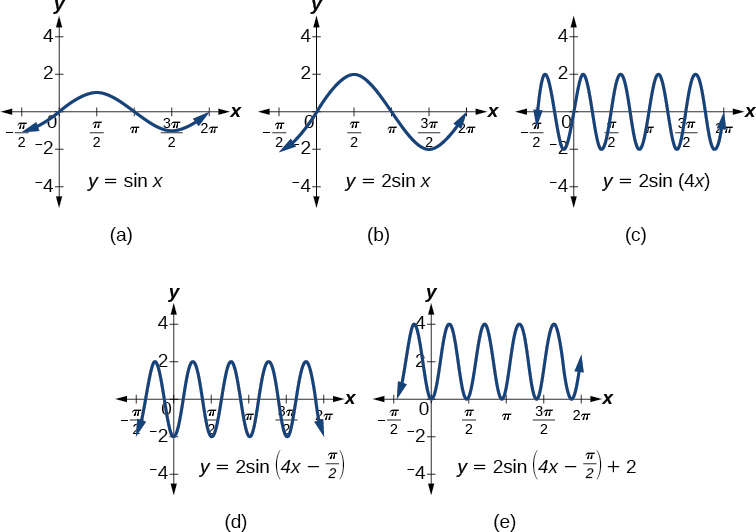
Grafu ya msingi ya$y=\sin x$
Kubadilisha amplitude kutoka 1 hadi 2 inazalisha grafu ya$y=2 \sin x$.
kipindi cha kazi sine mabadiliko na thamani ya$B,$ vile kwamba$\text{period}=\frac{2π}{B}.$ Hapa tuna$B=4,$ ambayo hutafsiri kwa kipindi cha$\frac{π}{2}$. Grafu inakamilisha mzunguko kamili katika$\frac{π}{2}$ vitengo.
Grafu inaonyesha mabadiliko ya usawa sawa na$\frac{C}{B}$, au$\frac{\frac{π}{2}}{4}=\frac{π}{8}$.
Hatimaye, grafu ni kubadilishwa vertically na thamani ya$D$. Katika kesi hii, grafu inabadilishwa na vitengo 2.

Mfano$\PageIndex{2}$: Finding the Amplitude and Period of a Function

Pata amplitude na kipindi cha kazi zifuatazo na grafu moja ya mzunguko.

$y=2 \sin (\frac{1}{4}x)$
$y=−3 \sin (2x+\frac{π}{2})$
$y= \cos x+3$

Suluhisho

Tutasuluhisha matatizo haya kulingana na mifano.

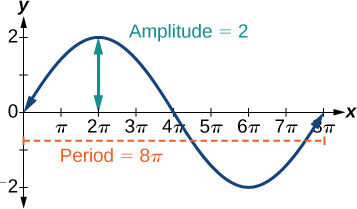
$y=2 \sin (\frac{1}{4}x)$inahusisha sine, hivyo sisi kutumia fomu\[y=A \sin (Bt+C)+D \nonumber\] Tunajua kwamba$| A |$ ni amplitude, hivyo amplitude ni 2. Kipindi ni$\frac{2π}{B}$ hivyo kipindi ni\[\begin{align*} \dfrac{2π}{B} &=\dfrac{2π}{\frac{1}{4}} \\ & =8π \end{align*}\] Angalia grafu katika Kielelezo$\PageIndex{3}$.

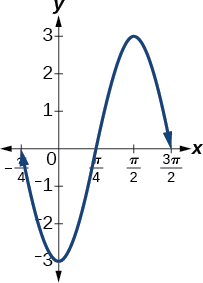
$y=−3 \sin(2x+ \frac{π}{2})$inahusisha sine, hivyo sisi kutumia aina\[y=A \sin (Bt−C)+D \nonumber\] Amplitude ni$| A |$, hivyo amplitude ni$|−3|=3.$ Tangu$A$ ni hasi, grafu ni yalijitokeza juu ya x -axis. Kipindi ni$\frac{2π}{B}$, hivyo kipindi ni Grafu\[\dfrac{2π}{B}=\dfrac{2π}{2}=π \nonumber\] inabadilishwa upande wa kushoto na$\frac{C}{B}=\frac{\frac{π}{2}}{2}=\frac{π}{4}$ vitengo. Angalia Kielelezo$\PageIndex{4}$.

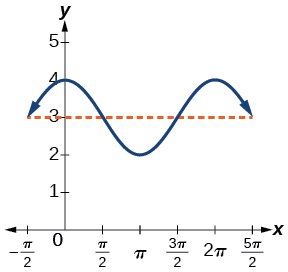
$y= \cos x+3$inahusisha cosine, hivyo tunatumia fomu
\[y=A \cos (Bt±C)+D \nonumber\]Amplitude ni$| A |$, hivyo amplitude ni 1 na kipindi ni$2π$ (Kielelezo$\PageIndex{5}$. Hii ni kazi ya kawaida ya cosine iliyobadilishwa vitengo vitatu.

Zoezi$\PageIndex{1}$:

Je! Ni amplitude na kipindi cha kazi gani$y=3 \cos (3πx)$?

Jibu: Amplitude ni$3,$ na kipindi ni$\frac{2}{3}$.

Kupata Equations na Graphing Sinusoidal Kazi

Njia moja ya kuchora kazi za sinusoidal ni kupata pointi tano muhimu. Vipengele hivi vinahusiana na vipindi vya urefu sawa unaowakilisha$\frac{1}{4}$ kipindi hicho. Pointi muhimu zitaonyesha eneo la maadili ya juu na ya chini. Ikiwa hakuna mabadiliko ya wima, wataonyesha pia x -intercepts. Kwa mfano, tuseme tunataka graph kazi$y=cos θ.$ Tunajua kwamba kipindi ni$2π$, hivyo sisi kupata muda kati ya pointi muhimu kama ifuatavyo.

\[\frac{2π}{4}=\frac{π}{2} \nonumber\]

Kuanzia na$θ=0,$ sisi kuhesabu kwanza y- thamani, kuongeza urefu wa muda$\frac{π}{2}$ kwa$0$, na kuhesabu pili y -thamani. Sisi kisha kuongeza$\frac{π}{2}$ mara kwa mara mpaka pointi tano muhimu ni kuamua. Thamani ya mwisho inapaswa kuwa sawa na thamani ya kwanza, kama mahesabu yanafunika kipindi kimoja kamili. Kufanya meza sawa na Jedwali$\PageIndex{1}$, tunaweza kuona pointi hizi muhimu wazi kwenye grafu iliyoonyeshwa kwenye Kielelezo$\PageIndex{6}$.

Jedwali$\PageIndex{1}$
$θ$	$0$	$\frac{π}{2}$	$π$	$\frac{3π}{2}$	$2π$
$y=\cos θ$	$1$	$0$	—1,1-1	$0$	$1$

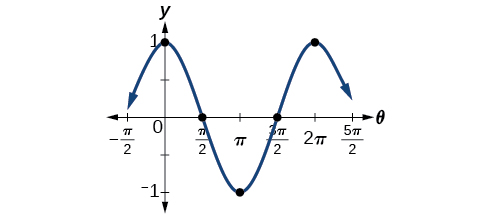
Mfano$\PageIndex{3}$: Graphing Sinusoidal Functions Using Key Points

Graph kazi$y=−4 \cos (πx)$ kwa kutumia amplitude, kipindi, na pointi muhimu.

Suluhisho

Amplitude ni$|−4|=4.$ Kipindi ni$\frac{2π}{ω}=\frac{2π}{π}=2.$ (Kumbuka kwamba wakati mwingine hutaja$B$ kama$ω.$) Mzunguko mmoja wa grafu unaweza kupatikana juu ya muda$[ 0,2 ]$. Ili kupata pointi muhimu, tunagawanya kipindi na 4. Fanya meza sawa na Kielelezo$\PageIndex{1}$:, kuanzia$x=0$ na kisha$\frac{1}{2}$ uongeze mfululizo$x$ na uhesabu$y.$ Angalia grafu katika Kielelezo$\PageIndex{7}$.

Jedwali$\PageIndex{1}$
$x$	$0$	$\frac{1}{2}$	$1$	$\frac{3}{2}$	$2$
$y=−4 \cos(πx)$	$−4$	$0$	$4$	$0$	$−4$

Zoezi$\PageIndex{2}$:

Grafu kazi$y=3 \sin(3x)$ kwa kutumia amplitude, kipindi, na pointi tano muhimu.

$x$	0	$\frac{π}{6}$	$\frac{π}{3}$	$\frac{π}{2}$	$\frac{2π}{3}$
$3 \sin (3x)$	0	3	0	-3	0


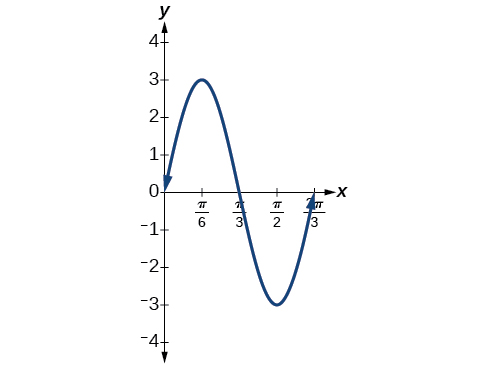
Jibu: $CNX_Precalc_Figure_07_07_004.jpg$
Kielelezo$\PageIndex{8}$

Modeling tabia ya mara kwa mara

Sasa tutatumia mawazo haya kwa matatizo yanayohusisha tabia ya mara kwa mara.

Mfano$\PageIndex{4}$: Modeling an Equation and Sketching a Sinusoidal Graph to Fit Criteria

Wastani wa joto la kila mwezi kwa mji mdogo huko Oregon hutolewa katika Jedwali$\PageIndex{1}$. Pata kazi ya sinusoidal ya fomu$y=A \sin (Bt−C)+D$ inayofaa data (pande zote hadi kumi ya karibu) na mchoro grafu.

Jedwali$\PageIndex{2}$
Mwezi	Joto,$^oF$
Januari	\ (^Ya\) "> 42.5
Februari	\ (^Ya\) "> 44.5
Machi	\ (^Ya\) "> 48.5
Aprili	\ (^Ya\) "> 52.5
Mei	\ (^Ya\) "> 58
Juni	\ (^Ya\) "> 63
Julai	\ (^Ya\) "> 68.5
Agosti	\ (^Ya\) "> 69
Septemba	\ (^Ya\) "> 64.5
Oktoba	\ (^Ya\) "> 55.5
Novemba	\ (^Ya\) "> 46.5
Desemba	\ (^Ya\) "> 43.5

Suluhisho

Kumbuka kwamba amplitude inapatikana kwa kutumia formula

\[A=\dfrac{\text{largest value −smallest value}}{2}\]

Hivyo, amplitude ni

\[\begin{align*} |A| & = \dfrac{69−42.5}{2} \\ &=13.25 \end{align*}\]

Data inashughulikia kipindi cha miezi 12, hivyo$\frac{2π}{B}=12$ inatoa$B=\frac{2π}{12}=\frac{π}{6}$.

Mabadiliko ya wima hupatikana kwa kutumia equation ifuatayo.

\[D=\dfrac{\text{highest value+lowest value}}{2}\]

Hivyo, mabadiliko ya wima ni

\[\begin{align*} D &= \dfrac{69+42.5}{2} &=55.8 \end{align*}\]

Hadi sasa, tuna equation$y=13.3 \sin (\frac{π}{6}x−C)+55.8$.

Ili kupata mabadiliko ya usawa, tunaingiza$x$ na$y$ maadili kwa mwezi wa kwanza na kutatua$C$.

\[\begin{align*} 42.5 & =13.3 \sin (\frac{π}{6}(1)−C)+55.8 \\ −13.3 & =13.3 \sin (\frac{π}{6}−C) \\ −1 & =\sin (\frac{π}{6}−C) \;\;\;\;\;\;\;\; \sin θ=−1→ θ=−\frac{π}{2} \\ \frac{π}{6}−C=−\frac{π}{2} \\ \frac{π}{6}+\frac{π}{2} & =C \\ &=\frac{2π}{3} \end{align*}\]

Tuna equation$y=13.3 \sin (\frac{π}{6}x−\frac{2π}{3})+55.8$. Angalia grafu katika Kielelezo$\PageIndex{9}$.

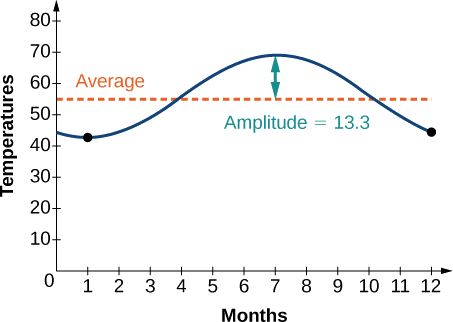
Mfano$\PageIndex{5}$: Describing Periodic Motion

saa mkono wa saa kubwa juu ya ukuta katika Union Station hatua 24 inches katika urefu. Saa sita mchana, ncha ya mkono wa saa ni inchi 30 kutoka dari. Saa 3 jioni, ncha ni inchi 54 kutoka dari, na saa 6 jioni, inchi 78. Saa 9 jioni, ni tena inchi 54 kutoka dari, na usiku wa manane, ncha ya mkono wa saa inarudi kwenye nafasi yake ya awali inchi 30 kutoka dari. Hebu$y$ sawa umbali kutoka ncha ya mkono wa saa hadi$x$ saa za dari baada ya mchana. Find equation kwamba mifano ya mwendo wa saa na mchoro grafu.

Suluhisho

Anza kwa kufanya meza ya maadili kama inavyoonekana katika Jedwali$\PageIndex{3}$.

Jedwali$\PageIndex{3}$
$x$	$y$	Pointi kwa njama
\ (x\) ">Mchana	\ (y\) "> 30 katika	$(0,30)$
\ (x\) ">3 PM	\ (y\) "> 54 katika	$(3,54)$
\ (x\) ">6 PM	\ (y\) "> 78 katika	$(6,78)$
\ (x\) ">9 PM	\ (y\) "> 54 katika	$(9,54)$
\ (x\) ">Usiku wa manane	\ (y\) "> 30 katika	$(12,30)$

Ili kutengeneza equation, sisi kwanza tunahitaji kupata amplitude.

\[\begin{align*} | A | & =| \dfrac{78−30}{2} | \\ &=24 \end{align*}\]

Mzunguko wa saa unarudia kila masaa 12. Hivyo,

\[\begin{align*} B &=\dfrac{2π}{12} \\ &= \dfrac{π}{6} \end{align*}\]

Mabadiliko ya wima ni

\[\begin{align*} D & = \dfrac{78+30}{2} \\ &=54 \end{align*}\]

Hakuna mabadiliko ya usawa, hivyo$C=0.$ Tangu kazi huanza na thamani ya chini ya$y$ wakati$x=0$ (kinyume na thamani ya juu), tutatumia kazi ya cosine na thamani hasi kwa$A$. Katika fomu$y=A \cos (Bx±C)+D,$ equation ni

\[y=−24 \cos (\dfrac{π}{6}x)+54\]

Angalia Kielelezo$\PageIndex{10}$.

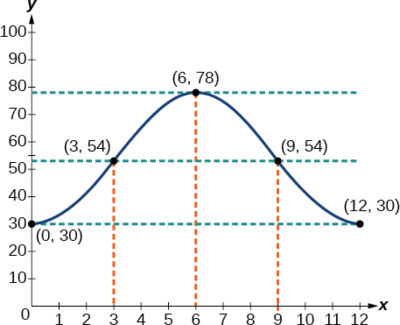
Mfano$\PageIndex{6}$: Determining a Model for Tides

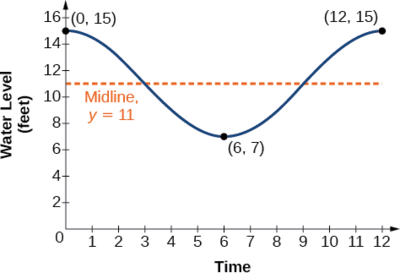
Urefu wa wimbi katika mji mdogo wa pwani hupimwa kando ya ukuta wa bahari. Viwango vya maji hupungua kati ya miguu 7 kwenye wimbi la chini na miguu 15 kwenye wimbi kubwa. Siku fulani, wimbi la chini lilitokea saa 6 asubuhi na wimbi kubwa lilitokea saa sita mchana. Takriban kila masaa 12, mzunguko unarudia. Find equation kwa mfano ngazi ya maji.

Suluhisho

Kama kiwango cha maji kinatofautiana kutoka futi 7 hadi 15, tunaweza kuhesabu amplitude kama

\[ \begin{align*} |A| &=| \frac{(15−7)}{2} | \\ & =4 \end{align*}\]

Mzunguko unarudia kila masaa 12; kwa hiyo,$B$ ni

\[\begin{align*} \dfrac{2π}{12}=\dfrac{π}{6} \end{align*}\]

Kuna tafsiri wima ya$\frac{(15+8)}{2}=11.5$. Kwa kuwa thamani ya kazi iko katika kiwango cha juu$t=0$, tutatumia kazi ya cosine, na thamani nzuri kwa$A$.

\[y=4 \cos (\dfrac{π}{6}) t+11 \nonumber\]

Angalia Kielelezo$\PageIndex{11}$.

Zoezi$\PageIndex{3}$:

joto kila siku katika mwezi wa Machi katika mji fulani inatofautiana kutoka chini ya$24°F$ hadi juu ya$40°F.$ Kupata kazi sinusoidal kwa mfano joto kila siku na mchoro grafu. Takriban wakati joto linafikia hatua ya kufungia$32 °F.$ Hebu$t=0$ inafanana na mchana.

Jibu: \[y=8 \sin (\frac{π}{12}t)+32 \nonumber\]
Joto hufikia kufungia saa sita mchana na usiku wa manane.

Zoezi$\PageIndex{4}$: Interpreting the Periodic Behavior Equation

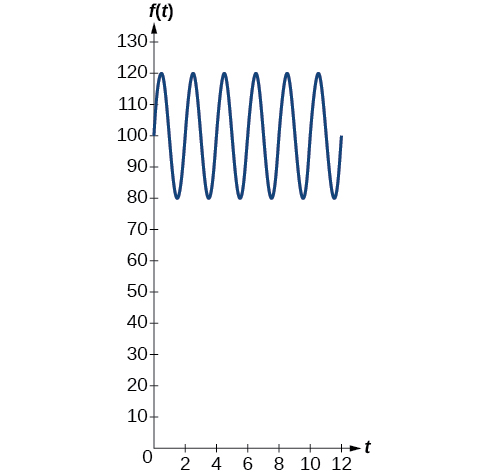
Shinikizo la damu la mtu wastani linatokana na kazi$f(t)=20 \sin (160πt)+100$, ambapo$f(t)$ inawakilisha shinikizo la damu kwa wakati$t$, kipimo kwa dakika. Tafsiri kazi kwa suala la kipindi na mzunguko. Mchoro grafu na upate kusoma shinikizo la damu.

Uchambuzi

Shinikizo la damu$\frac{120}{80}$ linachukuliwa kuwa la kawaida. Nambari ya juu ni kusoma kwa kiwango cha juu au systolic, ambayo inachukua shinikizo katika mishipa wakati moyo unapokubaliana. Nambari ya chini ni kusoma kwa kiwango cha chini au diastoli, ambayo hupima shinikizo katika mishipa kama moyo unapungua kati ya beats, kujaza na damu. Hivyo, shinikizo la kawaida la damu linaweza kuonyeshwa na kazi ya mara kwa mara na kiwango cha juu cha 120 na chini ya 80.

Mfano$\PageIndex{7}$: Interpreting the Periodic Behavior Equation

Suluhisho

Kipindi kinatolewa na

\[\begin{align*} \dfrac{2π}{ω} & = \dfrac{2π}{160π} \\ &=\dfrac{1}{80} \end{align*}\]

Katika kazi ya shinikizo la damu, mzunguko unawakilisha idadi ya kupigwa kwa moyo kwa dakika. Frequency ni usawa wa kipindi na hutolewa na

\[\begin{align*} \dfrac{ω}{2π} & = \dfrac{160π}{2π} \\ & =80 \end{align*}\]

Kielelezo$\PageIndex{12}$: shinikizo la damu kusoma kwenye grafu ni$\frac{120}{80} (\frac{\text{maximum}}{\text{minimum}})$.

Uchambuzi

Modeling Harmonic Motion Kazi

Harmonic mwendo ni aina ya mwendo wa mara kwa mara, lakini kuna mambo ya kuzingatia kwamba kutofautisha aina mbili. Wakati jumla ya maombi ya mara kwa mara mwendo mzunguko kupitia vipindi vyao na hakuna kuingiliwa nje, harmonic mwendo inahitaji nguvu kurejesha. Mifano ya mwendo harmonic ni pamoja na chemchemi, nguvu ya mvuto, na nguvu magnetic.

Rahisi Harmonic Motion

Aina ya mwendo inayoelezwa kama mwendo rahisi wa harmonic inahusisha nguvu ya kurejesha lakini inadhani kuwa mwendo utaendelea milele. Fikiria kitu mizigo kunyongwa juu ya spring, Wakati kitu kwamba si inasumbuliwa, tunasema kwamba kitu ni katika mapumziko, au katika usawa. Kama kitu ni vunjwa chini na kisha kutolewa, nguvu ya spring pulls kitu nyuma kuelekea usawa na harmonic mwendo huanza. Nguvu ya kurejesha ni sawa sawa na uhamisho wa kitu kutoka hatua yake ya usawa. Wakati$t=0,d=0.$

RAHISI HARMONIC MWENDO

Tunaona kwamba equations rahisi ya mwendo wa harmonic hutolewa kwa suala la uhamisho:

\[d=a \cos (ωt) \; \text{or} \; d=a \sin (ωt) \]

wapi$| a |$ amplitude,$\frac{2π}{ω}$ ni kipindi, na$\frac{ω}{2π}$ ni mzunguko, au idadi ya mizunguko kwa kitengo cha wakati.

Zoezi$\PageIndex{5}$: Finding the Displacement, Period, and Frequency, and Graphing a Function

Kwa kila kazi zilizopewa:

$y=5 \sin (3t)$
$y=6 \cos (πt)$
$y=5 \cos (\frac{π}{2}) t$

kushughulikia maswali yafuatayo:

Pata uhamisho wa juu wa kitu.
Pata kipindi au wakati unaohitajika kwa vibration moja.
Pata mzunguko.
Mchoro grafu.

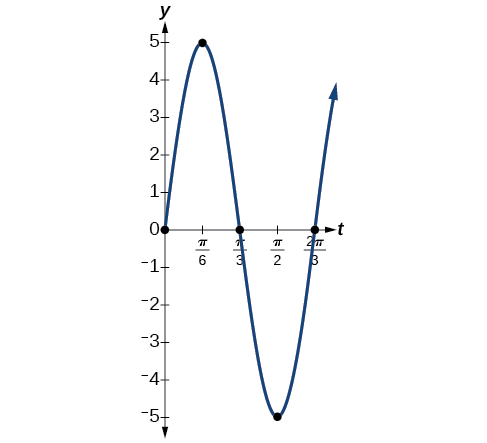
Grafu ya kazi y=5sin (3t) kutoka 0 hadi 2pi/3. pointi tano muhimu ni (0,0), (pi/6, 5), (pi/3, 0), (pi/2, -5), (2pi/3, 0). — Kielelezo$\PageIndex{13}$

Jibu

Uhamisho wa juu ni sawa na amplitude$ |a|$, ambayo ni 5.
Kipindi ni$\frac{2π}{ω}=\frac{2π}{3}$.
Mzunguko hutolewa kama$\frac{ω}{2π}=\frac{3}{2π}$.
Angalia Kielelezo$\PageIndex{13}$. Grafu inaonyesha pointi tano muhimu.

Jibu b

Uhamisho wa kiwango cha juu ni$6$.
Kipindi ni$\frac{2π}{ω}=\frac{2π}{π}=2.$
Mzunguko ni$\frac{ω}{2π}=\frac{π}{2π}=\frac{1}{2}.$
Angalia Kielelezo$\PageIndex{14}$.

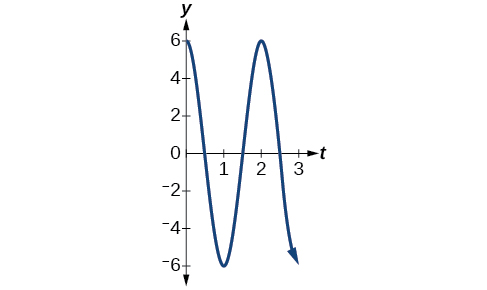
Grafu ya kazi y=6cos (pi t) kutoka 0 hadi 3. — Kielelezo$\PageIndex{14}$

Jibu c

Uhamisho wa kiwango cha juu ni$5$.
Kipindi ni$\frac{2π}{ω}=\frac{2π}{\frac{π}{2}}=4$.
Mzunguko ni$\frac{1}{4}.$
Angalia Kielelezo$\PageIndex{15}$.

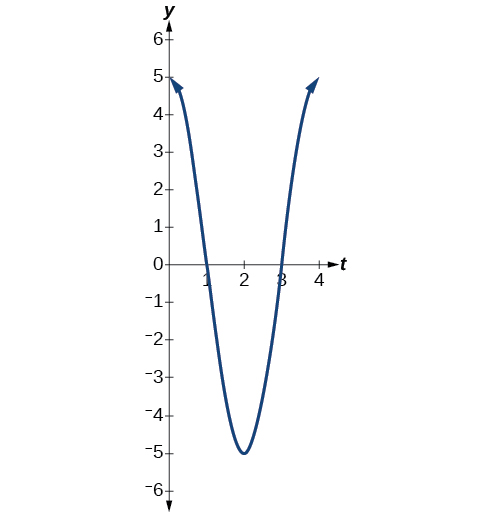
Grafu ya kazi y=5cos (pi/2 t) kutoka 0 hadi 4. — Kielelezo$\PageIndex{15}$

damped harmonic mwendo

Kwa kweli, pendulum haina swing na kurudi milele, wala kitu juu ya spring bounce juu na chini milele. Hatimaye, pendulum inacha kugeuza na kitu kinaacha bouncing na wote wanarudi kwenye usawa. Mwendo wa mara kwa mara ambao nguvu ya kutenganisha nishati, au sababu ya uchafu, vitendo hujulikana kama mwendo wa harmonic damped. Msuguano ni kawaida sababu damping.

Katika fizikia, formula mbalimbali hutumiwa kuhesabu sababu ya uchafu kwenye kitu cha kusonga. Baadhi ya hizi ni kanuni za mahesabu ambazo zinahusisha derivatives. Kwa madhumuni yetu, tutatumia formula kwa mifano ya msingi ya mwendo wa harmonic.

Ufafanuzi: Damped HARMONIC MOTION

Katika mwendo wa harmonic damped, uhamisho wa kitu cha oscillating kutoka nafasi yake ya kupumzika$t$ kwa wakati hutolewa kama

\[ f(t)=ae^{−ct} \sin (ωt) \; \text{ or} \; f(t)=ae^{−ct} \cos (ωt)\]

ambapo$c$ ni sababu damping,$|a|$ ni makazi ya awali na$\frac{2π}{ω}$ ni kipindi.

Mfano$\PageIndex{8}$: Modeling Damped Harmonic Motion

Mfano wa milinganyo inayofaa matukio mawili na kutumia matumizi ya graphing ili kuchora kazi: Mifumo miwili ya molekuli ya spring inaonyesha mwendo wa harmonic uliosababishwa kwa mzunguko wa mzunguko wa 0.5 kwa pili. Wote wawili wana uhamisho wa awali wa cm 10. Ya kwanza ina sababu ya uchafu ya 0.5 na ya pili ina sababu ya uchafu ya 0.1.

Suluhisho

Kwa wakati$t=0$, uhamisho ni kiwango cha juu cha cm 10, ambayo huita kazi ya cosine. Kazi ya cosine itatumika kwa mifano yote miwili.

Tunapewa mzunguko$f=\frac{ω}{2π}$ wa mzunguko wa 0.5 kwa pili. Hivyo,

\[\begin{align*} \dfrac{ω}{2π} &=0.5 \\ ω&=(0.5)2π \\ &=π \end{align*}\]

mfumo wa kwanza spring ina sababu damping ya$c=0.5$. Kufuatia mfano wa jumla kwa damped harmonic mwendo, tuna

\[f(t)=10e^{−0.5t} \cos (πt) \nonumber\]

Kielelezo$\PageIndex{16}$ mifano mwendo wa mfumo wa kwanza wa spring.

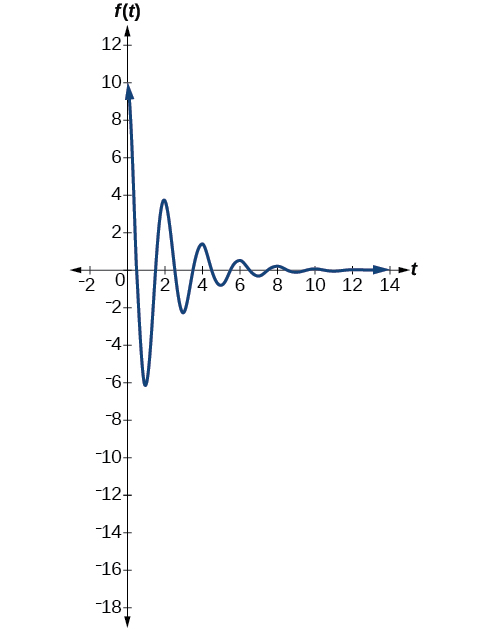
Grafu ya mfumo wa kwanza wa spring, f (t) = 10 (e^ (-.5t)) cos (pi*t), ambayo huanza na amplitude ya juu na inapungua haraka. — Kielelezo$\PageIndex{16}$

pili spring mfumo ina sababu damping ya$c=0.1$ na inaweza kuwa inatokana kama

\[f(t)=10e^{−0.1t} \cos (πt)\]

Kielelezo$\PageIndex{17}$ mifano mwendo wa mfumo wa pili wa spring.

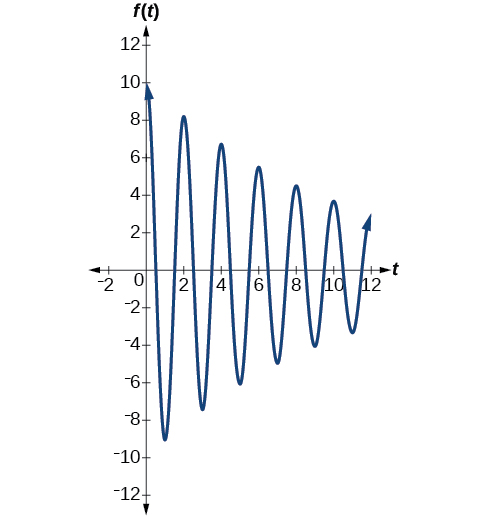
Grafu ya f (t) = 10 (e^ (-.1t)) cos (pi*t), ambayo huanza na amplitude ya juu na kupungua polepole (lakini ina mzunguko wa juu). — Kielelezo$\PageIndex{17}$

Uchambuzi

Angalia madhara tofauti ya mara kwa mara ya damping. Maadili ya kiwango cha juu na cha chini cha kazi na sababu ya uchafu$c=0.5$ hupungua kwa kasi zaidi kuliko ile ya kazi na$c=0.1$.

Zoezi$\PageIndex{6}$: Finding a Cosine Function that Models Damped Harmonic Motion

Pata na graph kazi ya fomu$y=ae^{−ct} \cos (ωt)$ inayoonyesha maelezo yaliyotolewa.

$a=20,c=0.05,p=4$
$a=2,c=1.5,f=3$

Suluhisho

Badilisha maadili yaliyotolewa katika mfano. Kumbuka kwamba kipindi ni$\frac{2π}{ω}$ na frequency ni$\frac{ω}{2π}$.

$y=20e^{−0.05t} \cos (\frac{π}{2}t).$Angalia Kielelezo$\PageIndex{18}$.

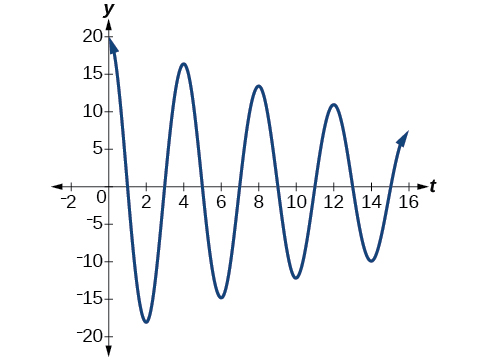
$Grafu ya f (t) = 20 (e^ (-.05t)) cos (pi/2 * t), ambayo huanza na amplitude ya juu na hupungua polepole.$
Kielelezo$\PageIndex{18}$
$y=2e^{−1.5t} \cos (6πt).$Angalia Kielelezo$\PageIndex{19}$.

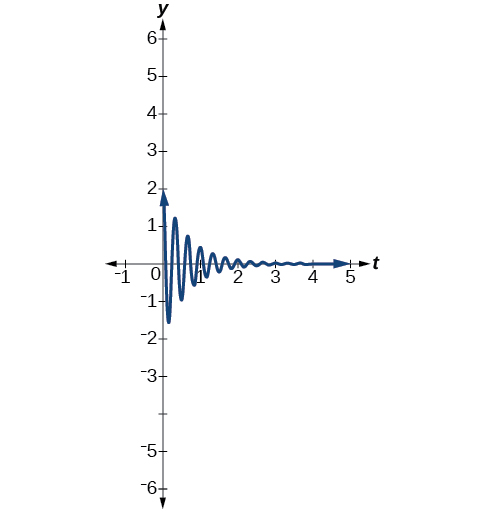
$Grafu ya f (t) = 2 (e^ (-1.5t)) cos (6pi * t), ambayo huanza na amplitude ndogo na hupungua haraka hadi karibu mstari wa moja kwa moja.$
Kielelezo$\PageIndex{19}$

Zoezi$\PageIndex{7}$

equation zifuatazo inawakilisha damped harmonic mwendo mfano:$f(t)=5e^{−6t} \cos (4t)$ Kupata makazi yao ya awali, damping mara kwa mara, na frequency.

Jibu: uhamisho wa awali =6, damping mara kwa mara = -6, frequency =$\frac{2}{π}$

Mfano$\PageIndex{9}$: Finding a Sine Function that Models Damped Harmonic Motion

Pata na graph kazi ya fomu$y=ae^{−ct} \sin (ωt)$ inayoonyesha maelezo yaliyotolewa.

$a=7,c=10,p=\frac{π}{6}$
$a=0.3,c=0.2,f=20$

Suluhisho

Tumia thamani ya$ω$ na ubadilishe maadili inayojulikana katika mfano.

Kama kipindi ni$\frac{2π}{ω}$, tuna
\[\begin{align*} \dfrac{π}{6} &=\dfrac{2π}{ω} \\ ωπ &=6(2π) \\ ω &=12 \end{align*}\]

Sababu ya uchafu hutolewa kama 10 na amplitude ni 7. Hivyo, mfano huo ni$y=7e^{−10t} \sin (12t)$. Angalia Kielelezo$\PageIndex{20}$.

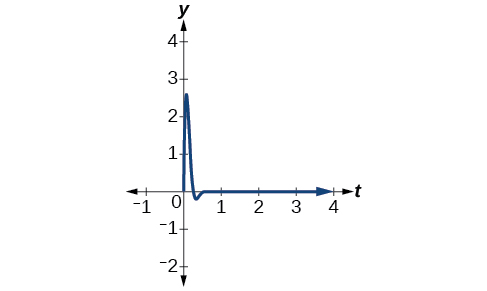
$Grafu ya f (t) = 7 (e^ (-10t)) dhambi (12t), ambayo spikes karibu na t=0 na haraka inakuwa karibu mstari wa moja kwa moja.$
Kielelezo$\PageIndex{20}$
Kama frequency ni$\frac{ω}{2π}$, tuna
\[\begin{align*} 20 &=\dfrac{ω}{2π} \\ 40π &=ω \end{align*}\]

sababu damping ni kutolewa kama$0.2$ na amplitude ni$0.3.$ mfano ni$y=0.3e^{−0.2t} \sin (40πt).$ Angalia Kielelezo$\PageIndex{21}$.

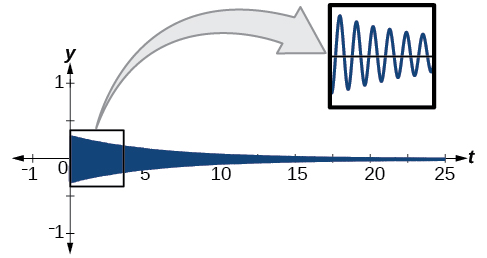
$Grafu ya f (t) = .3e^ (-.2t) dhambi (40pi*t), ambayo ina amplitude ndogo lakini inapungua haraka hadi kuonekana kwa mstari wa moja kwa moja. Mzunguko ni wa juu sana kwamba, katika kiwango hiki, kazi inaonekana kama sura imara. Zoom katika kukatwa kwa grafu inaonyesha picha halisi ya sinusoidal ya kazi.$
Kielelezo$\PageIndex{21}$

Uchambuzi

Ulinganisho wa mifano miwili iliyopita inaonyesha jinsi tunavyochagua kati ya kazi za sine au cosine ili kuiga vigezo vya sinusoidal. Tunaona kwamba kazi cosine ni katika makazi yao ya kiwango cha juu wakati$t=0$, na kazi sine ni katika hatua msawazo wakati$t=0.$ Kwa mfano, fikiria equation$y=20e^{−0.05t} \cos (\frac{π}{2}t)$ kutoka Mfano. Tunaweza kuona kutoka grafu kwamba wakati$t=0,y=20,$ ambayo ni amplitude ya awali. Angalia hii kwa kuweka$t=0$ katika equation ya cosine:

\[ \begin{align*} y &=20e^{−0.05(0)} \cos (\frac{π}{2})(0) \\ &=20(1)(1) \\ & =20 \end{align*}\]

Kutumia mazao ya kazi ya sine

\[\begin{align*} y &=20e^{−0.05(0)} \sin (\frac{π}{2})(0) \\ & =20(1)(0) \\ &=0 \end{align*}\]

Hivyo, cosine ni kazi sahihi.

Zoezi$\PageIndex{8}$:

Andika equation kwa damped harmonic mwendo aliyopewa$a=10,c=0.5$, na$p=2.$

Jibu: $y=10e^{−0.5t} \cos (πt)$

Mfano$\PageIndex{10}$: Modeling the Oscillation of a Spring

Spring kupima inchi 10 katika urefu wa asili ni USITUMIE na inchi 5 na kutolewa. Inapunguza mara moja kila sekunde 3, na amplitude yake inapungua kwa 30% kila pili. Kupata equation kwamba mifano ya nafasi ya$t$ sekunde spring baada ya kutolewa.

Suluhisho

Amplitude huanza saa 5 katika. na hupungua 30% kila pili. Kwa sababu chemchemi ya awali imesisitizwa, tutaandika A kama thamani hasi. Tunaweza kuandika sehemu ya amplitude ya kazi kama

\[A(t)=5(1−0.30)^t \nonumber\]

Sisi kuweka$(1−0.30)^t$ katika fomu$e^{ct}$ kama ifuatavyo:

\[\begin{align*} 0.7 &=e^c \\ c &= \ln .7 \\ c & =−0.357 \end{align*}\]

Sasa hebu tuseme kipindi hicho. Mzunguko wa spring kupitia nafasi zake kila sekunde 3, hii ni kipindi, na tunaweza kutumia formula ili kupata omega.

\[\begin{align*} 3 &= \dfrac{2π}{ω} \\ ω &= \dfrac{2π}{3} \end{align*}\]

Urefu wa asili wa inchi 10 ni midline. Tutatumia kazi ya cosine, tangu chemchemi inapoanza katika uhamisho wake wa juu. Sehemu hii ya equation inawakilishwa kama

\[y=\cos (\dfrac{2π}{3}t)+10 \nonumber\]

Hatimaye, sisi kuweka kazi zote mbili pamoja. Yetu mfano wa nafasi ya spring kwa$t$ sekunde hutolewa kama

\[y=−5e^{−0.357t} \cos (\dfrac{2π}{3}t)+10 \nonumber\]

Angalia grafu katika Kielelezo$\PageIndex{22}$.

Grafu ya kazi y = -5e^ (-.35t) cos (2pi/3 t) + 10 kutoka 0 hadi 24. Inaanza kama mawimbi yenye amplitude ya juu na hupungua hadi karibu mstari wa moja kwa moja haraka sana. — Kielelezo$\PageIndex{22}$

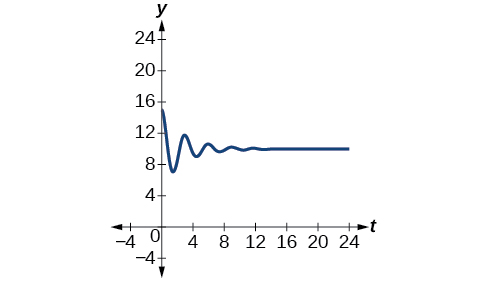
Zoezi$\PageIndex{9}$

Masi imesimamishwa kutoka chemchemi hufufuliwa umbali wa cm 5 juu ya nafasi yake ya kupumzika. Masi hutolewa kwa wakati$t=0$ na kuruhusiwa kufuta. Baada ya$\frac{1}{3}$ pili, inazingatiwa kuwa wingi unarudi kwenye nafasi yake ya juu. Pata kazi ya kuiga mwendo huu kuhusiana na nafasi yake ya kupumzika ya awali.

Jibu: $y=5 \cos (6πt)$

Kwa mujibu wa Vigezo Kutokana

Kamba ya gitaa huvunjwa na hutetemeka katika mwendo wa harmonic damped. Kamba ni vunjwa na kuhamishwa 2 cm kutoka nafasi yake ya kupumzika. Baada ya sekunde 3, uhamisho wa kamba hupima cm 1. Pata mara kwa mara ya damping.

Suluhisho

Sababu ya uhamisho inawakilisha amplitude na imedhamiriwa na mgawo$ae^{−ct}$ katika mfano wa mwendo wa harmonic damped. Mara kwa mara ya damping ni pamoja na katika muda$e^{−ct}$. Inajulikana kuwa baada ya sekunde 3, kiwango cha juu cha mitaa kina nusu ya thamani yake ya awali. Kwa hiyo, tuna equation

\[ae^{−c(t+3)}=\dfrac{1}{2} ae^{−ct}\]

Matumizi algebra na sheria ya exponents kutatua kwa$c$.

\[\begin{array}{cl} ae^{−c(t+3)}=\frac{1}{2}ae^{−ct} \\ e^{−ct}⋅e^{−3c}=\frac{1}{2}e^{−ct} & \text{Divide out } a. \\ e^{−3c}=\frac{1}{2} & \text{Divide out }e^{−ct}. \\ e^{3c}=2 & \text{Take reciprocals.} \end{array}\]

Kisha kutumia sheria za logarithms.

\[\begin{align*} e^{3c} &=2 \\ 3c &=\ln 2 \\ c & =\frac{\ln 2}{3} \end{align*}\]

Mara kwa mara ya damping ni$\frac{\ln 2}{3}$.

Bounding Curves katika Harmonic Motion

Harmonic mwendo grafu inaweza kuwa iliyoambatanishwa na curves bounding. Wakati kazi ina amplitude tofauti, kama kwamba amplitude kuongezeka na maporomoko mara nyingi ndani ya kipindi, tunaweza kuamua curves bounding kutoka sehemu ya kazi.

Mfano$\PageIndex{12}$: Graphing an Oscillating Cosine Curve

Graph kazi$f(x)=\cos (2πx) \cos (16πx)$.

Suluhisho

Grafu iliyozalishwa na kazi hii itaonyeshwa katika sehemu mbili. Grafu ya kwanza itakuwa kazi halisi$f(x)$ (angalia Mchoro$\PageIndex{23; top}$;), na grafu ya pili ni kazi halisi$f(x)$ pamoja na kazi ya kuzuia (angalia Mchoro$\PageIndex{23; bottom}$). Grafu zinaonekana tofauti kabisa.

Grafu ya f (x) = cos (2pi*x) cos (16pi*x), kazi ya sinusoidal inayoongezeka na kupungua amplitude yake mara kwa mara. — Figure_07_07_016.jpg "->

Kielelezo$\PageIndex{23}$

Uchambuzi

Curves$y=\cos (2πx)$ na$y=−\cos (2πx)$ ni bounding curves: wao amefungwa kazi kutoka juu na chini, kufuatilia nje pointi ya juu na chini. Grafu ya mwendo wa harmonic inakaa ndani ya curves ya mipaka. Huu ni mfano wa kazi ambayo amplitude haipungua tu kwa wakati, lakini kwa kweli huongezeka na hupungua mara nyingi ndani ya kipindi.

Mlinganyo muhimu


Aina ya kawaida ya equation ya sinusoidal	$y=A \sin (Bt−C)+D \text{ or } y=A \cos (Bt−C)+D$
Rahisi harmonic mwendo	$d=a \cos (ωt) \text{ or } d=a \sin (ωt) $
Damped harmonic mwendo	$f(t)=ae^{−ct} \sin (ωt) \text{ or } f(t)=ae^{−ct} \cos (ωt)$

Dhana muhimu

Kazi za sinusoidal zinawakilishwa na grafu za sine na cosine. Kwa fomu ya kawaida, tunaweza kupata mabadiliko ya amplitude, kipindi, na usawa na wima. Angalia Mfano na Mfano.
Tumia pointi muhimu kwa grafu kazi ya sinusoidal. Vipengele vitano muhimu ni pamoja na maadili ya chini na ya juu na maadili ya midline. Angalia Mfano.
Kazi za mara kwa mara zinaweza kutengeneza matukio yanayotokea tena katika mizunguko iliyowekwa, kama awamu za mwezi, mikono juu ya saa, na misimu kwa mwaka. Angalia Mfano, Mfano, Mfano na Mfano.
Kazi za mwendo wa Harmonic zinatokana na data iliyotolewa. Sawa na maombi ya mwendo wa mara kwa mara, mwendo wa harmonic inahitaji nguvu ya kurejesha. Mifano ni pamoja na nguvu ya mvuto na mwendo wa spring ulioamilishwa kwa uzito. Angalia Mfano.
Damped harmonic mwendo ni aina ya tabia ya mara kwa mara walioathirika na sababu damping. Sababu za kusambaza nishati, kama msuguano, husababisha uhamisho wa kitu kupungua. Angalia Mfano, Mfano, Mfano, na Mfano.
Bounding curves delineate grafu ya mwendo harmonic na kutofautiana kiwango cha juu na maadili ya chini. Angalia Mfano.

\(θ\)	\(0\)	\(\frac{π}{2}\)	\(π\)	\(\frac{3π}{2}\)	\(2π\)
\(y=\cos θ\)	\(1\)	\(0\)	—1,1-1	\(0\)	\(1\)

\(x\)	\(0\)	\(\frac{1}{2}\)	\(1\)	\(\frac{3}{2}\)	\(2\)
\(y=−4 \cos(πx)\)	\(−4\)	\(0\)	\(4\)	\(0\)	\(−4\)

\(x\)	0	\(\frac{π}{6}\)	\(\frac{π}{3}\)	\(\frac{π}{2}\)	\(\frac{2π}{3}\)
\(3 \sin (3x)\)	0	3	0	-3	0

\(x\)	\(y\)	Pointi kwa njama
\ (x\) ">Mchana	\ (y\) "> 30 katika	\((0,30)\)
\ (x\) ">3 PM	\ (y\) "> 54 katika	\((3,54)\)
\ (x\) ">6 PM	\ (y\) "> 78 katika	\((6,78)\)
\ (x\) ">9 PM	\ (y\) "> 54 katika	\((9,54)\)
\ (x\) ">Usiku wa manane	\ (y\) "> 30 katika	\((12,30)\)

Aina ya kawaida ya equation ya sinusoidal	\(y=A \sin (Bt−C)+D \text{ or } y=A \cos (Bt−C)+D\)
Rahisi harmonic mwendo	\(d=a \cos (ωt) \text{ or } d=a \sin (ωt) \)
Damped harmonic mwendo	\(f(t)=ae^{−ct} \sin (ωt) \text{ or } f(t)=ae^{−ct} \cos (ωt)\)