7.5: Kutatua equations ya Trigonometric

Malengo ya kujifunza

• Tatua equations linear trigonometric katika sine na cosine.
• Tatua equations inayohusisha kazi moja ya trigonometric.
• Tatua equations ya trigonometric kwa kutumia calculator.
• Tatua equations ya trigonometric ambayo ni quadratic katika fomu.
• Tatua equations trigonometric kutumia utambulisho wa msingi.
• Tatua usawa wa trigonometric na pembe nyingi.
• Tatua matatizo ya pembetatu ya kulia.

Thales wa Miletus (karibu 625—547 KK) anajulikana kama mwanzilishi wa jiometri. Hadithi ni kwamba alihesabu urefu wa Piramidi Kuu ya Giza nchini Misri kwa kutumia nadharia ya pembetatu sawa, ambayo aliiendeleza kwa kupima kivuli cha wafanyakazi wake. Kulingana na uwiano, nadharia hii ina maombi katika maeneo kadhaa, ikiwa ni pamoja na jiometri ya fractal, uhandisi, na usanifu. Mara nyingi, angle ya mwinuko na angle ya unyogovu hupatikana kwa kutumia pembetatu sawa.

Kielelezo$\PageIndex{1}$: piramidi za Misri wamesimama karibu na mji wa kisasa (mikopo: Oisin Mulvihill)

Katika sehemu za awali za sura hii, tuliangalia utambulisho wa trigonometric. Utambulisho ni kweli kwa maadili yote katika uwanja wa kutofautiana. Katika sehemu hii, tunaanza utafiti wetu wa equations trigonometric kujifunza matukio halisi ya dunia kama vile kutafuta vipimo vya piramidi.

Kutatua equations Linear Trigonometric katika Sine na Cosine

Ulinganifu wa trigonometric ni, kama jina linamaanisha, equations zinazohusisha kazi za trigonometric. Sawa kwa njia nyingi za kutatua equations ya polynomial au equations ya busara, maadili maalum tu ya kutofautiana yatakuwa ufumbuzi, ikiwa kuna ufumbuzi wakati wote. Mara nyingi sisi kutatua equation trigonometric juu ya muda maalum. Hata hivyo, kama mara nyingi, tutatakiwa kupata ufumbuzi wote iwezekanavyo, na kama kazi za trigonometric ni mara kwa mara, ufumbuzi hurudiwa ndani ya kila kipindi. Kwa maneno mengine, equations ya trigonometric inaweza kuwa na idadi isiyo na kipimo cha ufumbuzi. Zaidi ya hayo, kama usawa wa busara, uwanja wa kazi lazima uzingatiwe kabla ya kudhani kuwa suluhisho lolote halali. Kipindi cha kazi zote za sine na kazi ya cosine ni$2\pi$. Kwa maneno mengine, kila$2\pi$ vitengo, y- maadili kurudia. Ikiwa tunahitaji kupata ufumbuzi wote unaowezekana, basi lazima tuongeze$2\pi k$,$k$ wapi integer, kwa suluhisho la awali. Kumbuka utawala ambayo inatoa format kwa kusema ufumbuzi wote iwezekanavyo kwa ajili ya kazi ambapo kipindi ni$2\pi$:

$$\sin \theta=\sin(\theta \pm 2k\pi)$$

Kuna sheria sawa za kuonyesha ufumbuzi wote unaowezekana kwa kazi nyingine za trigonometric. Kutatua equations trigonometric inahitaji mbinu sawa na kutatua equations algebraic. Tunasoma equation kutoka kushoto kwenda kulia, usawa, kama sentensi. Tunatafuta mifumo inayojulikana, sababu, kupata denominators ya kawaida, na kubadilisha maneno fulani na kutofautiana ili kutatua mchakato wa moja kwa moja zaidi. Hata hivyo, kwa usawa wa trigonometric, tuna pia faida ya kutumia utambulisho tuliotengeneza katika sehemu zilizopita.

Mfano$\PageIndex{1A}$: Solving a Linear Trigonometric Equation Involving the Cosine Function

Kupata ufumbuzi wote inawezekana halisi kwa equation$\cos \theta=\dfrac{1}{2}$.

Suluhisho

Kutoka kwenye mduara wa kitengo, tunajua kwamba

$$\begin{align*} \cos \theta &=\dfrac{1}{2} \\[4pt] \theta &=\dfrac{\pi}{3},\space \dfrac{5\pi}{3} \end{align*}$$

Hizi ni ufumbuzi katika kipindi hicho$[ 0,2\pi ]$. Ufumbuzi wote unaowezekana hutolewa na

$$\theta=\dfrac{\pi}{3} \pm 2k\pi \quad \text{and} \quad \theta=\dfrac{5\pi}{3} \pm 2k\pi \nonumber$$

$k$wapi integer.

Mfano$\PageIndex{1B}$: Solving a Linear Equation Involving the Sine Function

Kupata ufumbuzi wote inawezekana halisi kwa equation$\sin t=\dfrac{1}{2}$.

Suluhisho

Kutatua kwa maadili yote iwezekanavyo ya$t$ njia ambazo ufumbuzi ni pamoja na pembe zaidi ya kipindi cha$2\pi$. Kutoka kwenye sehemu ya Utambulisho wa Sum na Tofauti, tunaweza kuona kwamba ufumbuzi ni$t=\dfrac{\pi}{6}$ na$t=\dfrac{5\pi}{6}$. Lakini tatizo ni kuomba maadili yote iwezekanavyo ambayo kutatua equation. Kwa hiyo, jibu ni

$$t=\dfrac{\pi}{6}\pm 2\pi k \quad \text{and} \quad t=\dfrac{5\pi}{6}\pm 2\pi k \nonumber$$

$k$wapi integer.

Jinsi ya: Kutokana na equation ya trigonometric, tatua kutumia algebra

1. Angalia kwa mfano kwamba unaonyesha mali algebraic, kama vile tofauti ya mraba au nafasi factoring.
2. Badilisha kujieleza kwa trigonometric na variable moja, kama vile$x$ au$u$.
3. Kutatua equation njia sawa equation algebraic itakuwa kutatuliwa.
4. Badilisha kujieleza kwa trigonometric nyuma kwa kutofautiana katika maneno yanayotokana.
5. Tatua kwa angle.

Mfano$\PageIndex{2}$: Solve the Linear Trigonometric Equation

Kutatua equation hasa:$2 \cos \theta−3=−5$,$0≤\theta<2\pi$.

Suluhisho

Tumia mbinu za algebraic kutatua equation.

$$\begin{align*} 2 \cos \theta-3&= -5\\ 2 \cos \theta&= -2\\ \cos \theta&= -1\\ \theta&= \pi \end{align*}$$

Zoezi$\PageIndex{2}$

Kutatua hasa yafuatayo equation linear juu ya muda$[0,2\pi)$:$2 \sin x+1=0$.

Jibu

$x=\dfrac{7\pi}{6},\space \dfrac{11\pi}{6}$

Kutatua Equations Kuhusisha Kazi moja ya Trigonometric

Tunapopewa equations zinazohusisha moja tu ya kazi sita za trigonometric, ufumbuzi wao unahusisha kutumia mbinu za algebraic na mduara wa kitengo (angalia [kiungo]). Tunahitaji kufanya masuala kadhaa wakati equation inahusisha kazi trigonometric isipokuwa sine na cosine. Matatizo yanayohusisha usawa wa kazi za msingi za trigonometric zinahitajika kutazamwa kwa mtazamo wa algebraic. Kwa maneno mengine, tutaandika kazi ya usawa, na kutatua kwa pembe kwa kutumia kazi. Pia, equation inayohusisha kazi ya tangent ni tofauti kidogo na moja iliyo na kazi ya sine au cosine. Kwanza, kama tunavyojua, kipindi cha tangent ni$\pi$, sio$2\pi$. Zaidi ya hayo, uwanja wa tangent ni namba zote halisi isipokuwa idadi isiyo ya kawaida ya integer ya$\dfrac{\pi}{2}$, isipokuwa, bila shaka, tatizo linaweka vikwazo vyake kwenye uwanja.

Mfano$\PageIndex{3A}$: Solving a Problem Involving a Single Trigonometric Function

Tatua tatizo hasa:$2 {\sin}^2 \theta−1=0$,$0≤\theta<2\pi$.

Suluhisho

Kama tatizo hili halijafanywa kwa urahisi, tutatatua kutumia mali ya mizizi ya mraba. Kwanza, tunatumia algebra kujitenga$\sin \theta$. Kisha tutapata pembe.

\ [kuanza {align*}
2 {\ dhambi} ^2\ theta-1&= 0\\
2 {\ dhambi} ^2\ theta&= 1\\
{\ dhambi} ^2\ theta&=\ dfrac {1} {2}\\ sqrt {
\ dhambi} ^2\ theta} &=\ pm\ sqrt {\ dfrac {1} {2} {\ dhambi}}\
\ dhambi\ theta&=\ pm\ dfrac {1} {\ sqrt {2}}\\
&=\ pm\ dfrac {\ sqrt {2}} {2}\\ theta&=\ dfrac {\ pi} {4},\ nafasi\ dfrac {3\ pi} {4},\ space\ dfrac {5
\ pi} {4}\]

Mfano$\PageIndex{3B}$: Solving a Trigonometric Equation Involving Cosecant

Kutatua equation zifuatazo hasa:$\csc \theta=−2$,$0≤\theta<4\pi$.

Suluhisho

Tunataka maadili yote ambayo$\theta$ kwa$\csc \theta=−2$ muda$0≤\theta<4\pi$.

$$\begin{align*} \csc \theta&= -2\\ \dfrac{1}{\sin \theta}&= -2\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\space \dfrac{11\pi}{6},\space \dfrac{19\pi}{6}, \space \dfrac{23\pi}{6} \end{align*}$$

Uchambuzi

Kama$\sin \theta=−\dfrac{1}{2}$, angalia kwamba ufumbuzi wote wanne ni katika quadrants ya tatu na ya nne.

Mfano$\PageIndex{3C}$: Solving an Equation Involving Tangent

Kutatua equation hasa:$\tan\left(\theta−\dfrac{\pi}{2}\right)=1$,$0≤\theta<2\pi$.

Suluhisho

Kumbuka kwamba kazi tangent ina kipindi cha$\pi$. Kwa muda$[ 0,\pi )$, na kwa pembe ya$\dfrac{\pi}{4}$, tangent ina thamani ya$1$. Hata hivyo, angle tunayotaka ni$\left(\theta−\dfrac{\pi}{2}\right)$. Hivyo, kama$\tan\left(\dfrac{\pi}{4}\right)=1$, basi

$$\begin{align*} \theta-\dfrac{\pi}{2}&= \dfrac{\pi}{4}\\ \theta&= \dfrac{3\pi}{4} \pm k\pi \end{align*}$$

Zaidi ya muda$[ 0,2\pi )$, tuna ufumbuzi wawili:

$\theta=\dfrac{3\pi}{4}$na$\theta=\dfrac{3\pi}{4}+\pi=\dfrac{7\pi}{4}$

Zoezi$\PageIndex{3}$

Kupata ufumbuzi wote kwa ajili ya$\tan x=\sqrt{3}$.

Jibu

$\dfrac{\pi}{3}\pm \pi k$

Mfano$\PageIndex{4}$: Identify all Solutions to the Equation Involving Tangent

Kutambua ufumbuzi wote halisi kwa equation$2(\tan x+3)=5+\tan x$,$0≤x<2\pi$.

Suluhisho

Tunaweza kutatua equation hii kwa kutumia algebra tu. Sulua maneno$\tan x$ upande wa kushoto wa ishara sawa.

$$\begin{align*} 2(\tan x)+2(3)&= 5+\tan x\\ 2\tan x+6&= 5+\tan x\\ 2\tan x-\tan x&= 5-6\\ \tan x&= -1 \end{align*}$$

Kuna pembe mbili kwenye mduara kitengo ambayo thamani tangent ya$−1$:$\theta=\dfrac{3\pi}{4}$ na$\theta=\dfrac{7\pi}{4}$.

Tatua Ulinganifu wa Trigonometric Kutumia Calculator

Sio kazi zote zinaweza kutatuliwa hasa kwa kutumia mduara wa kitengo tu. Wakati tunapaswa kutatua equation kuwashirikisha angle zaidi ya moja ya pembe maalum, tutahitaji kutumia calculator. Hakikisha imewekwa kwa hali sahihi, ama digrii au radians, kulingana na vigezo vya tatizo lililopewa.

Mfano$\PageIndex{5A}$: Using a Calculator to Solve a Trigonometric Equation Involving Sine

Tumia calculator kutatua equation$\sin \theta=0.8$, ambapo$\theta$ ni katika radians.

Suluhisho

Kuhakikisha mode ni kuweka radians. Ili kupata$\theta$, tumia kazi ya sine inverse. Kwa mahesabu mengi, unahitaji kushinikiza kifungo cha 2 ^ND na kisha kifungo cha SIN ili kuleta${\sin}^{−1}$ kazi. Ni nini kinachoonyeshwa kwenye skrini${\sin}^{−1}$ ni.Calculator iko tayari kwa pembejeo ndani ya mabano. Kwa tatizo hili, tunaingia${\sin}^{−1}(0.8)$, na waandishi wa habari kuingia. Hivyo, kwa decimals nne maeneo,

${\sin}^{−1}(0.8)≈0.9273$

Suluhisho ni

$\theta≈0.9273\pm 2\pi k$

Upimaji wa angle katika digrii ni

$$\begin{align*} \theta&\approx 53.1^{\circ}\\ \theta&\approx 180^{\circ}-53.1^{\circ}\\ &\approx 126.9^{\circ} \end{align*}$$

Uchambuzi

Kumbuka kuwa calculator itarudi tu angle katika quadrants I au IV kwa kazi ya sine, kwa kuwa hiyo ni aina ya sine inverse. Pembe nyingine inapatikana kwa kutumia$\pi−\theta$.

Mfano$\PageIndex{5B}$: Using a Calculator to Solve a Trigonometric Equation Involving Secant

Kutumia calculator kutatua equation$\sec θ=−4,$ kutoa jibu lako katika radians.

Suluhisho

Tunaweza kuanza na algebra fulani.

$$\begin{align*} \sec \theta&= -4\\ \dfrac{1}{\cos \theta}&= -4\\ \cos \theta&= -\dfrac{1}{4} \end{align*}$$

Angalia kwamba MODE iko katika radians. Sasa tumia kazi ya cosine inverse

$$\begin{align*}{\cos}^{-1}\left(-\dfrac{1}{4}\right)&\approx 1.8235\\ \theta&\approx 1.8235+2\pi k \end{align*}$$

Tangu$\dfrac{\pi}{2}≈1.57$ na$\pi≈3.14$,$1.8235$ ni kati ya namba hizi mbili, hivyo$\theta≈1.8235$ ni katika roboduara II. Cosine pia ni hasi katika quadrant III. Kumbuka kwamba calculator itarudi tu angle katika quadrants I au II kwa kazi ya cosine, kwa kuwa hiyo ni aina ya cosine inverse. Angalia Kielelezo$\PageIndex{2}$.

Kielelezo$\PageIndex{2}$

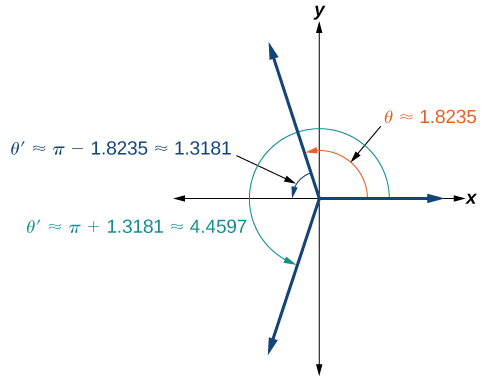
Kwa hiyo, tunahitaji pia kupata kipimo cha angle katika quadrant III. Katika quadrant III, angle ya kumbukumbu ni$\theta '≈\pi−1.8235≈1.3181$. Suluhisho lingine katika quadrant III ni$\theta '≈\pi+1.3181≈4.4597$.

Ufumbuzi ni$\theta≈1.8235\pm 2\pi k$ na$\theta≈4.4597\pm 2\pi k$.

Zoezi$\PageIndex{5}$

Kutatua$\cos \theta=−0.2$.

Jibu

$\theta≈1.7722\pm 2\pi k$na$\theta≈4.5110\pm 2\pi k$

Kutatua Ulinganifu wa Trigonometric katika Fomu ya Quadratic

Kutatua equation quadratic inaweza kuwa ngumu zaidi, lakini kwa mara nyingine tena, tunaweza kutumia algebra kama sisi ingekuwa kwa equation yoyote quadratic. Angalia mfano wa equation. Je, kuna kazi zaidi ya moja ya trigonometric katika equation, au kuna moja tu? Ni kazi gani ya trigonometric ni mraba? Ikiwa kuna kazi moja tu iliyowakilishwa na moja ya maneno ni mraba, fikiria juu ya fomu ya kawaida ya quadratic. Badilisha nafasi ya trigonometric na variable kama vile$x$ au$u$. Kama badala hufanya equation kuangalia kama equation quadratic, basi tunaweza kutumia mbinu sawa kwa ajili ya kutatua quadratic kutatua equations trigonometric.

Mfano$\PageIndex{6A}$: Solving a Trigonometric Equation in Quadratic Form

Kutatua equation hasa:${\cos}^2 \theta+3 \cos \theta−1=0$,$0≤\theta<2\pi$.

Suluhisho

Tunaanza kwa kutumia mbadala na kuchukua nafasi$\cos \theta$ na$x$. Sio lazima kutumia mbadala, lakini inaweza kufanya tatizo iwe rahisi kutatua kuibua. Hebu$\cos \theta=x$. Tuna

$x^2+3x−1=0$

Equation haiwezi kuhesabiwa, hivyo tutatumia formula ya quadratic:$x=\dfrac{−b\pm \sqrt{b^2−4ac}}{2a}$.

$$\begin{align*} x&= \dfrac{ -3\pm \sqrt{ {(-3)}^2-4 (1) (-1) } }{2}\\ &= \dfrac{-3\pm \sqrt{13}}{2}\end{align*}$$

Badilisha nafasi$x$$\cos \theta$ na kutatua.

$$\begin{align*} \cos \theta&= \dfrac{-3\pm \sqrt{13}}{2}\\ \theta&= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right) \end{align*}$$

Kumbuka kuwa tu ishara + hutumiwa. Hii ni kwa sababu tunapata hitilafu tunapotatua$\theta={\cos}^{−1}\left(\dfrac{−3−\sqrt{13}}{2}\right)$ kwenye calculator, kwani uwanja wa kazi ya cosine inverse ni$[ −1,1 ]$. Hata hivyo, kuna suluhisho la pili:

$$\begin{align*} \theta&= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right)\\ &\approx 1.26 \end{align*}$$

Sehemu hii ya mwisho ya angle iko katika quadrant I. tangu cosine pia ni chanya katika quadrant IV, ufumbuzi wa pili ni

$$\begin{align*} \theta&= 2\pi-{\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right)\\ &\approx 5.02 \end{align*}$$

Mfano$\PageIndex{6B}$: Solving a Trigonometric Equation in Quadratic Form by Factoring

Kutatua equation hasa:$2 {\sin}^2 \theta−5 \sin \theta+3=0$,$0≤\theta≤2\pi$.

Suluhisho

Kutumia kikundi, quadratic hii inaweza kuhesabiwa. Labda kufanya badala halisi,$\sin \theta=u$, au fikiria, kama sisi sababu:

$$\begin{align*} 2 {\sin}^2 \theta-5 \sin \theta+3&= 0\\ (2 \sin \theta-3)(\sin \theta-1)&= 0 \qquad \text {Now set each factor equal to zero.}\\ 2 \sin \theta-3&= 0\\ 2 \sin \theta&= 3\\ \sin \theta&= \dfrac{3}{2}\\ \sin \theta-1&= 0\\ \sin \theta&= 1 \end{align*}$$

Next kutatua kwa$\theta$:$\sin \theta≠\dfrac{3}{2}$, kama aina mbalimbali ya kazi sine ni$[ −1,1 ]$. Hata hivyo$\sin \theta=1$, kutoa suluhisho$\theta=\dfrac{\pi}{2}$.

Uchambuzi

Hakikisha kuangalia ufumbuzi wote kwenye uwanja uliopewa kama baadhi ya mambo hayana suluhisho.

Zoezi$\PageIndex{6}$

Kutatua${\sin}^2 \theta=2 \cos \theta+2$,$0≤\theta≤2\pi$. [Kidokezo: Fanya mbadala ya kueleza equation tu kwa suala la cosine.]

Jibu

$\cos \theta=−1$,$\theta=\pi$

Mfano$\PageIndex{7A}$: Solving a Trigonometric Equation Using Algebra

Tatua hasa:$2 {\sin}^2 \theta+\sin \theta=0;\space 0≤\theta<2\pi$

Suluhisho

Tatizo hili linapaswa kuonekana ukoo kama ni sawa na quadratic. Hebu$\sin \theta=x$. Equation inakuwa$2x^2+x=0$. Tunaanza kwa kuzingatia:

\ [kuanza {align*}
2x ^ 2+x&= 0\\
x (2x+1) &= 0\ qquad\ maandishi {Weka kila kipengele sawa na sifuri.} \\
x&= 0\\
2x+1&= 0\\
x&= -\ dfrac {1} {2}\ mwisho {align*}\]
Kisha, mbadala nyuma katika equation kujieleza awali$\sin \theta$ kwa$x$. Hivyo,
\ [kuanza {align*}\ dhambi\ theta&= 0
\\\ theta&= 0,
\ pi\\ dhambi\ theta&= -
\ dfrac {1} {2}\\ theta&=\ dfrac {7\ pi} {6}
\\ mwisho {align*}\]

Ufumbuzi ndani ya uwanja$0≤\theta<2\pi$ ni$\theta=0,\pi,\dfrac{7\pi}{6},\dfrac{11\pi}{6}$.

Kama tunapendelea si mbadala, tunaweza kutatua equation kwa kufuata mfano huo wa factoring na kuweka kila sababu sawa na sifuri.

$$\begin{align*} {\sin}^2 \theta+\sin \theta&= 0\\ \sin \theta(2\sin \theta+1)&= 0\\ \sin \theta&= 0\\ \theta&= 0,\pi\\ 2 \sin \theta+1&= 0\\ 2\sin \theta&= -1\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\dfrac{11\pi}{6} \end{align*}$$

Uchambuzi

Tunaweza kuona ufumbuzi kwenye grafu katika Kielelezo$\PageIndex{3}$. Kwa muda$0≤\theta<2\pi$, grafu huvuka$x$ mhimili mara nne, katika ufumbuzi uliotajwa. Angalia kwamba milinganyo ya trigonometric ambayo iko katika fomu ya quadratic inaweza kutoa hadi ufumbuzi nne badala ya mbili zinazotarajiwa ambazo hupatikana kwa equations quadratic. Katika mfano huu, kila suluhisho (angle) sambamba na thamani nzuri ya sine itazalisha pembe mbili ambazo zingeweza kusababisha thamani hiyo.

Kielelezo$\PageIndex{3}$

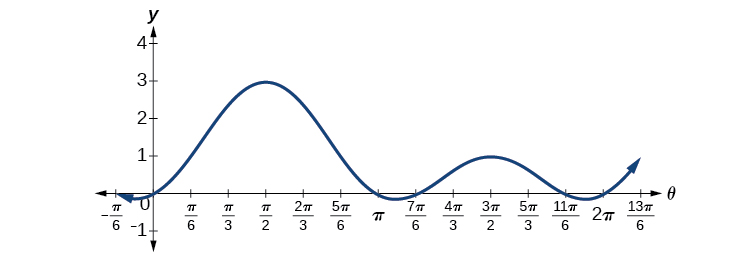
Tunaweza kuthibitisha ufumbuzi juu ya mduara kitengo katika kupitia matokeo katika sehemu ya Sum na Tofauti Identifies pamoja.

Mfano$\PageIndex{7B}$: Solving a Trigonometric Equation Quadratic in Form

Tatua quadratic equation kwa fomu hasa:$2 {\sin}^2 \theta−3 \sin \theta+1=0$,$0≤\theta<2\pi$.

Suluhisho

Tunaweza kuzingatia kutumia kikundi. Maadili ya ufumbuzi wa$\theta$ yanaweza kupatikana kwenye mduara wa kitengo.

$$\begin{align*} (2 \sin \theta-1)(\sin \theta-1)&= 0\\ 2 \sin \theta-1&= 0\\ \sin \theta&= \dfrac{1}{2}\\ \theta&= \dfrac{\pi}{6}, \dfrac{5\pi}{6}\\ \sin \theta&= 1\\ \theta&= \dfrac{\pi}{2} \end{align*}$$

Zoezi$\PageIndex{7}$

Tatua equation ya quadratic$2{\cos}^2 \theta+\cos \theta=0$.

Jibu

$\dfrac{\pi}{2}, \space \dfrac{2\pi}{3}, \space \dfrac{4\pi}{3}, \space \dfrac{3\pi}{2}$

Kutatua Ulinganifu wa Trigonometric Kutumia Utambulisho wa

Wakati algebra inaweza kutumika kutatua idadi ya equations trigonometric, tunaweza pia kutumia utambulisho msingi kwa sababu wao kufanya kutatua equations rahisi. Kumbuka kwamba mbinu tunazotumia kutatua si sawa na zile za kuthibitisha utambulisho. Sheria za msingi za algebra zinatumika hapa, kinyume na kuandika upya upande mmoja wa utambulisho ili kufanana na upande mwingine. Katika mfano unaofuata, tunatumia utambulisho mbili ili kurahisisha equation.

Mfano$\PageIndex{8A}$: Use Identities to Solve an Equation

Kutumia utambulisho wa kutatua hasa equation trigonometric juu ya muda$0≤x<2\pi$.

$\cos x \cos(2x)+\sin x \sin(2x)=\dfrac{\sqrt{3}}{2}$

Suluhisho

Angalia kwamba upande wa kushoto wa equation ni formula tofauti kwa cosine.

$$\begin{align*} \cos x \cos(2x)+\sin x \sin(2x)&= \dfrac{\sqrt{3}}{2}\\ \cos(x-2x)&= \dfrac{\sqrt{3}}{2}\qquad \text{Difference formula for cosine}\\ \cos(-x)&= \dfrac{\sqrt{3}}{2}\qquad \text{Use the negative angle identity.}\\ \cos x&= \dfrac{\sqrt{3}}{2} \end{align*}$$

Kutoka kwenye mduara wa kitengo katika sehemu ya Utambulisho wa Sum na Tofauti, tunaona kwamba$\cos x=\dfrac{\sqrt{3}}{2}$ wakati$x=\dfrac{\pi}{6},\space \dfrac{11\pi}{6}$.

Mfano$\PageIndex{8B}$: Solving the Equation Using a Double-Angle Formula

Kutatua equation hasa kwa kutumia formula mbili-angle:$\cos(2\theta)=\cos \theta$.

Suluhisho

Tuna uchaguzi wa maneno matatu ya mbadala ya pembe mbili za cosine. Kama ni rahisi kutatua kwa kazi moja ya trigonometric kwa wakati mmoja, tutachagua utambulisho wa angle mbili unaohusisha cosine tu:

$$\begin{align*} \cos(2\theta)&= \cos \theta\\ 2{\cos}^2 \theta-1&= \cos \theta\\ 2 {\cos}^2 \theta-\cos \theta-1&= 0\\ (2 \cos \theta+1)(\cos \theta-1)&= 0\\ 2 \cos \theta+1&= 0\\ \cos \theta&= -\dfrac{1}{2}\\ \cos \theta-1&= 0\\ \cos \theta&= 1 \end{align*}$$

Hivyo, kama$\cos \theta=−\dfrac{1}{2}$, basi$\theta=\dfrac{2\pi}{3}\pm 2\pi k$ na$\theta=\dfrac{4\pi}{3}\pm 2\pi k$; kama$\cos \theta=1$, basi$\theta=0\pm 2\pi k$.

Mfano$\PageIndex{8C}$: Solving an Equation Using an Identity

Tatua equation hasa kwa kutumia utambulisho:$3 \cos \theta+3=2 {\sin}^2 \theta$,$0≤\theta<2\pi$.

Suluhisho

Ikiwa tunaandika upya upande wa kulia, tunaweza kuandika equation kwa suala la cosine:

\ [kuanza {align*}
3\ cos\ theta+3&= 2 {\ dhambi} ^2\ theta\\
3\ cos\ theta+3&= 2 (1- {\ cos} ^2\ theta)\\
3\ cos\ theta+3&= 2-2 {\ cos} ^2\ theta\\
2 {\ cos} ^2\ theta+3\ cos\ ta+1&= 0\\
(2\ cos\ theta+1) (\ cos\ theta+1) &= 0\\
2\\ cos\\ theta+1&= 0
\\ cos\ theta&= -\
dfrac {1} {2}\\ theta&=\ dfrac {2\\ pi} {3},\ nafasi\
\ dfrac {4\\ pi} {3}\\ cos\
\ theta&=\ pi\
\ mwisho {align*}\]

Ufumbuzi wetu ni$\theta=\dfrac{2\pi}{3},\space \dfrac{4\pi}{3},\space \pi$.

Kutatua equations ya Trigonometric na Angles nyingi

Wakati mwingine haiwezekani kutatua equation ya trigonometric na utambulisho ambao una angle nyingi, kama vile$\sin(2x)$ au$\cos(3x)$. Wakati wanakabiliwa na equations hizi, kumbuka kwamba$y=\sin(2x)$ ni compression usawa kwa sababu ya 2 ya kazi$y=\sin x$. Katika kipindi cha$2\pi$, tunaweza graph vipindi viwili vya$y=\sin(2x)$, kinyume na mzunguko mmoja wa$y=\sin x$. Ukandamizaji huu wa grafu unatuongoza kuamini kunaweza kuwa na mara mbili ya x -intercepts au ufumbuzi wa$\sin(2x)=0$ ikilinganishwa na$\sin x=0$. Taarifa hii itatusaidia kutatua equation.

Mfano$\PageIndex{9}$: Solving a Multiple Angle Trigonometric Equation

Tatua hasa:$\cos(2x)=\dfrac{1}{2}$ juu$[ 0,2\pi )$.

Suluhisho

Tunaweza kuona kwamba equation hii ni equation kiwango na nyingi ya angle. Kama$\cos(\alpha)=\dfrac{1}{2}$, tunajua$\alpha$ ni katika quadrants I na IV. Wakati tu$\theta={\cos}^{−1} \dfrac{1}{2}$ kutoa ufumbuzi katika quadrants I na II, tunatambua kwamba ufumbuzi wa equation$\cos \theta=\dfrac{1}{2}$ itakuwa katika quadrants I na IV.

Kwa hiyo, pembe zinazowezekana ni$\theta=\dfrac{\pi}{3}$ na$\theta=\dfrac{5\pi}{3}$. Hivyo,$2x=\dfrac{\pi}{3}$ au$2x=\dfrac{5\pi}{3}$, ambayo ina maana kwamba$x=\dfrac{\pi}{6}$ au$x=\dfrac{5\pi}{6}$. Je, hii ina maana? Ndiyo, kwa sababu$\cos\left(2\left(\dfrac{\pi}{6}\right)\right)=\cos\left(\dfrac{\pi}{3}\right)=\dfrac{1}{2}$.

Je, kuna majibu mengine yanayowezekana? Hebu kurudi hatua yetu ya kwanza.

Katika roboduara mimi$2x=\dfrac{\pi}{3}$, hivyo$x=\dfrac{\pi}{6}$ kama ilivyoelezwa. Hebu tuzunguka mduara tena:

\ [kuanza {align*}
2x&=\ dfrac {\ pi} {3} +2\ pi\\
&=\ dfrac {\ pi} {3} +\ dfrac {6\ pi} {3}\\
&=\ dfrac {7\ pi} {7\\\
maandishi {3\ pi} {6}\\ Nakala {7\
\ Nakala {Moja zaidi mzunguko mavuno}\\
2x&=\ dfrac {\ pi} {3} +4\ pi\\
& ; =\ dfrac {\ pi} {3} +\ dfrac {12\ pi} {3}\\
&=\ dfrac {13\ pi} {3}\
\ mwisho {align*}\]

$x=\dfrac{13\pi}{6}>2\pi$, hivyo thamani hii kwa$x$ ni kubwa kuliko$2\pi$, hivyo si ufumbuzi juu ya$[ 0,2\pi )$.

Katika roboduara IV$2x=\dfrac{5\pi}{3}$, hivyo$x=\dfrac{5\pi}{6}$ kama ilivyoelezwa. Hebu tuzunguka mduara tena:

$$\begin{align*} 2x&= \dfrac{5\pi}{3}+2\pi\\ &= \dfrac{5\pi}{3}+\dfrac{6\pi}{3}\\ &= \dfrac{11\pi}{3} \end{align*}$$

hivyo$x=\dfrac{11\pi}{6}$.

Moja zaidi ya mzunguko wa mavuno

$$\begin{align*} 2x&= \dfrac{5\pi}{3}+4\pi\\ &= \dfrac{5\pi}{3}+\dfrac{12\pi}{3}\\ &= \dfrac{17\pi}{3} \end{align*}$$

$x=\dfrac{17\pi}{6}>2\pi$, hivyo thamani hii kwa$x$ ni kubwa kuliko$2\pi$, hivyo si ufumbuzi juu ya$[ 0,2\pi )$.

Ufumbuzi wetu ni$x=\dfrac{\pi}{6}, \space \dfrac{5\pi}{6}, \space \dfrac{7\pi}{6}$, na$\dfrac{11\pi}{6}$. Kumbuka kwamba wakati wowote sisi kutatua tatizo katika mfumo wa$sin(nx)=c$, ni lazima kwenda kuzunguka$n$ mara kitengo mduara.

Kutatua Matatizo ya Triangle

Sasa tunaweza kutumia njia zote ambazo tumejifunza kutatua matatizo ambayo yanahusisha kutumia mali ya pembetatu sahihi na Theorem ya Pythagorean. Tunaanza na Theorem ya kawaida ya Pythagorean,

$$a^2+b^2=c^2 \label{Pythagorean}$$

na mfano equation na kifafa hali.

Mfano$\PageIndex{10A}$: Using the Pythagorean Theorem to Model an Equation

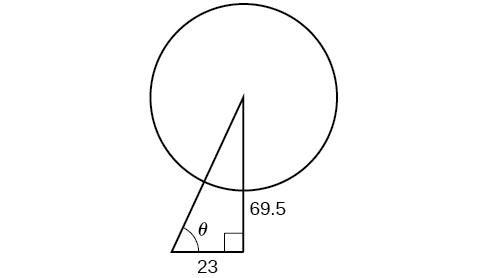
Moja ya nyaya ambazo zinaweka katikati ya gurudumu la London Eye Ferris chini lazima kubadilishwa. Katikati ya gurudumu la Ferris ni$69.5$ mita juu ya ardhi, na nanga ya pili chini ni$23$ mita kutoka chini ya gurudumu la Ferris. Takriban cable ni muda gani, na ni angle gani ya mwinuko (kutoka chini hadi katikati ya gurudumu la Ferris)? Angalia Kielelezo$\PageIndex{4}$.

Kielelezo$\PageIndex{4}$

Suluhisho

Tumia Theorem ya Pythagorean (Equation\ ref {Pythagorean}) na mali ya pembetatu sahihi ili kutengeneza equation inayofaa tatizo. Kutumia habari iliyotolewa, tunaweza kuteka pembetatu sahihi. Tunaweza kupata urefu wa cable na Theorem ya Pythagorean.

$$\begin{align*} a^2+b^2&= c^2\\ {(23)}^2+{(69.5)}^2&\approx 5359\\ \sqrt{5359}&\approx 73.2\space m \end{align*}$$

Pembe ya mwinuko ni$\theta$, iliyoundwa na nanga ya pili chini na cable inayofikia katikati ya gurudumu. Tunaweza kutumia kazi ya tangent ili kupata kipimo chake. Pande zote kwa maeneo mawili ya decimal.

$$\begin{align*} \tan \theta&= 69.523\\ {\tan}^{-1}(69.523)&\approx 1.2522\\ &\approx 71.69^{\circ} \end{align*}$$

Pembe ya mwinuko ni takriban$71.7°$, na urefu wa cable ni$73.2$ mita.

Mfano$\PageIndex{10B}$: Using the Pythagorean Theorem to Model an Abstract Problem

Kanuni za usalama wa OSHA zinahitaji kwamba msingi wa ngazi$1$ uweke mguu kutoka ukuta kwa kila$4$ miguu ya urefu wa ngazi. Pata angle ambayo ngazi ya urefu wowote huunda na ardhi na urefu ambao ngazi inagusa ukuta.

Suluhisho

Kwa urefu wowote wa ngazi, msingi unahitaji kuwa umbali kutoka ukuta sawa na moja ya nne ya urefu wa ngazi. Vilevile, ikiwa msingi wa ngazi ni “” miguu kutoka ukuta, urefu wa ngazi itakuwa$4a$ miguu. Angalia Kielelezo$\PageIndex{5}$.

Kielelezo$\PageIndex{5}$

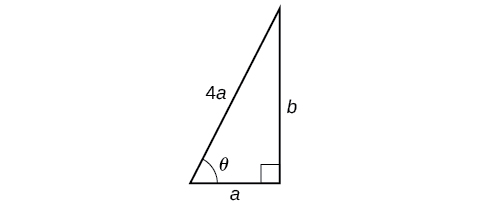
Kando karibu$a$ na$\theta$ ni na hypotenuse ni$4a$. Hivyo,

$$\begin{align*} \cos \theta&= \dfrac{a}{4a}\\ &= \dfrac{1}{4}\\ {\cos}^{-1}\left (\dfrac{1}{4}\right )&\approx 75.5^{\circ} \end{align*}$$

Uinuko wa ngazi huunda angle ya$75.5°$ ardhi. Urefu ambao ngazi inagusa ukuta inaweza kupatikana kwa kutumia Theorem ya Pythagorean:

$$\begin{align*} a^2+b^2&= {(4a)}^2\\ b^2&= {(4a)}^2-a^2\\ b^2&= 16a^2-a^2\\ b^2&= 15a^2\\ b&= a\sqrt{15} \end{align*}$$

Hivyo, ngazi inagusa ukuta kwa$a\sqrt{15}$ miguu kutoka chini.

Media

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kutatua equations ya trigonometric.

• Kutatua Ulinganisho wa Trigonometric I
• Kutatua Ulinganifu wa Trigonometric II
• Kutatua Ulinganisho wa Trigonometric III
• Kutatua Ulinganisho wa Trigonometric IV
• Kutatua Ulinganisho wa Trigonometric V
• Kutatua Ulinganisho wa Trigonometric VI

Dhana muhimu

• Wakati wa kutatua equations linear trigonometric, tunaweza kutumia mbinu algebraic kama sisi kufanya kutatua equations algebraic. Angalia mwelekeo, kama tofauti ya mraba, fomu ya quadratic, au maneno ambayo yanajitokeza vizuri badala. Angalia Mfano$\PageIndex{1}$, Mfano$\PageIndex{2}$, na Mfano$\PageIndex{3}$.
• Ulinganifu unaohusisha kazi moja ya trigonometric inaweza kutatuliwa au kuthibitishwa kwa kutumia mduara wa kitengo. Angalia Mfano$\PageIndex{4}$, Mfano$\PageIndex{5}$, na Mfano$\PageIndex{6}$, na Mfano$\PageIndex{7}$.
• Tunaweza pia kutatua equations trigonometric kwa kutumia calculator graphing. Angalia Mfano$\PageIndex{8}$ na Mfano$\PageIndex{9}$.
• Ulinganifu wengi huonekana quadratic katika fomu. Tunaweza kutumia badala ya kufanya equation kuonekana rahisi, na kisha kutumia mbinu sawa sisi kutumia kutatua quadratic algebraic: factoring, formula quadratic, nk Angalia Mfano$\PageIndex{10}$$\PageIndex{11}$, Mfano$\PageIndex{12}$, na Mfano$\PageIndex{13}$.
• Tunaweza pia kutumia utambulisho kutatua equation trigonometric. Angalia Mfano$\PageIndex{14}$, Mfano$\PageIndex{15}$, na Mfano$\PageIndex{16}$.
• Tunaweza kutumia badala ya kutatua equation ya trigonometric ya angle nyingi, ambayo ni compression ya kazi ya kawaida ya trigonometric. Tutahitaji kuzingatia ukandamizaji na kuthibitisha kwamba tumepata ufumbuzi wote kwa muda uliopewa. Angalia Mfano$\PageIndex{17}$.
• Matukio halisi ya ulimwengu yanaweza kutengenezwa na kutatuliwa kwa kutumia Theorem ya Pythagorean na kazi za trigonometric. Angalia Mfano$\PageIndex{18}$.