5.3: Usambazaji Sare

Usambazaji sare ni usambazaji wa uwezekano unaoendelea na unahusika na matukio ambayo yanaweza kutokea. Wakati wa kufanya kazi nje ya matatizo ambayo yana usambazaji sare, kuwa makini kutambua kama data ni ya pamoja au ya kipekee.

Mfano 5.3.1

Takwimu katika Jedwali$\PageIndex{1}$ ni mara 55 za kusisimua, kwa sekunde, za mtoto mwenye umri wa wiki nane.

Jedwali$\PageIndex{1}$

10.4	19.6	18.8	13.9	17.8	16.8	21.6	17.9	12.5	11.1	4.9
12.8	14.8	22.8	20.0	15.9	16.3	13.4	17.1	14.5	19.0	22.8
1.3	0.7	8.9	11.9	10.9	7.3	5.9	3.7	17.9	19.2	9.8
5.8	6.9	2.6	5.8	21.7	11.8	3.4	2.1	4.5	6.3	10.7
8.9	9.4	9.4	7.6	10.0	3.3	6.7	7.8	11.6	13.8	18.6

Sampuli inamaanisha = 11.49 na kupotoka kwa kiwango cha sampuli = 6.23.

Tutafikiri kwamba nyakati za kusisimua, kwa sekunde, kufuata usambazaji sare kati ya sifuri na sekunde 23, pamoja. Hii ina maana kwamba wakati wowote wa kusisimua kutoka sifuri hadi na ikiwa ni pamoja na sekunde 23 ni uwezekano sawa. Histogram ambayo inaweza kujengwa kutoka sampuli ni usambazaji wa maandishi unaofanana na usambazaji wa sare ya kinadharia.

Hebu$X =$ urefu, kwa sekunde, ya tabasamu ya mtoto mwenye umri wa wiki nane.

Uthibitisho wa usambazaji sare ni

$X \sim U(a, b)$ambapo thamani$a =$ ya chini ya$x$ na thamani$b =$ ya juu ya$x$.

Kazi ya wiani ya uwezekano ni$f(x) = \frac{1}{b-a}$ kwa$a \leq x \leq b$.

Kwa mfano huu,$X \sim U(0, 23)$ na$f(x) = \frac{1}{23-0}$ kwa$0 \leq X \leq 23$.

Fomu kwa maana ya kinadharia na kupotoka kwa kiwango ni

$$\mu = \frac{a+b}{2} \nonumber$$

na

$$\sigma = \sqrt{\frac{(b-a)^{2}}{12}} \nonumber$$

Kwa tatizo hili, maana ya kinadharia na kupotoka kwa kiwango ni

$$\mu = \frac{0+23}{2} = 11.50 \, seconds \nonumber$$

na

$$\sigma = \frac{(23-0)^{2}}{12} = 6.64\, seconds. \nonumber$$

Kumbuka kwamba maana ya kinadharia na kupotoka kwa kiwango ni karibu na sampuli maana na kupotoka kwa kiwango katika mfano huu.

Zoezi$\PageIndex{1}$

Takwimu zinazofuata ni idadi ya abiria kwenye boti 35 za uvuvi tofauti za mkataba. Sampuli inamaanisha = 7.9 na kupotoka kwa kiwango cha sampuli = 4.33. Takwimu zinafuata usambazaji sare ambapo maadili yote kati na ikiwa ni pamoja na sifuri na 14 yana uwezekano sawa. Hali maadili ya na$b$. Andika usambazaji kwa nukuu sahihi, na uhesabu maana ya kinadharia na kupotoka kwa kawaida.

Jedwali$\PageIndex{2}$

1	12	4	10	4	14	11
7	11	4	13	2	4	6
3	10	0	12	6	9	10
5	13	4	10	14	12	11
6	10	11	0	11	13	2

Jibu

$a$ni sifuri;$b$ ni$14$$X \sim U (0, 14)$;$\mu = 7$ abiria;$\sigma = 4.04$ abiria

Mfano 5.3.2A

a Rejea Mfano 5.3.1. Je! Ni uwezekano gani kwamba mtoto mwenye umri wa wiki nane aliyechaguliwa kwa nasibu anasisimua kati ya sekunde mbili na 18?

Jibu

a. kupata$P(2 < x < 18)$.

$P(2 < x < 18) = (\text{base})(\text{height}) = (18 – 2)\left(\frac{1}{23}\right) = \left(\frac{16}{23}\right)$.

Kielelezo$\PageIndex{1}$

Zoezi$\PageIndex{2}$B

b Pata asilimia 90 ^ya muda wa mtoto mwenye umri wa wiki nane.

Jibu

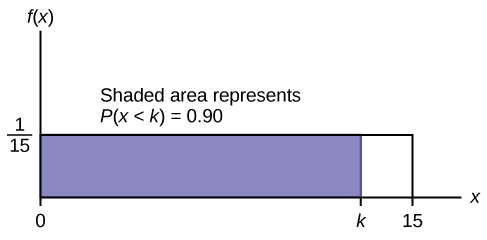
b. asilimia tisini ya mara smiling kuanguka chini ya asilimia 90 ^th$k$, hivyo$P(x < k) = 0.90$

$$P(x < k)= 0.90$$

$$(\text{base})(\text{height}) = 0.90$$

$$(k−0)\left(\frac{1}{23}\right) = 0.90$$

$$k = (23)(0.90) = 20.7$$

Kielelezo$\PageIndex{2}$

Zoezi$\PageIndex{3}$C

pata uwezekano kwamba mtoto mwenye umri wa wiki nane anasisimua zaidi ya sekunde 12 akijua kwamba mtoto anasisimua zaidi ya sekunde nane.

Jibu

c Swali hili la uwezekano ni masharti. Unaulizwa kupata uwezekano kwamba mtoto mwenye umri wa wiki nane anasisimua zaidi ya sekunde 12 wakati tayari unajua mtoto ametabasamu kwa sekunde zaidi ya nane.

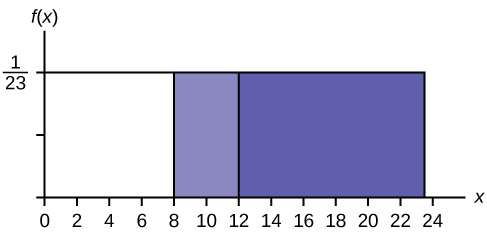
Tafuta$P(x > 12 | x > 8)$ Kuna njia mbili za kufanya tatizo. Kwa njia ya kwanza, tumia ukweli kwamba hii ni masharti na kubadilisha nafasi ya sampuli. Grafu inaonyesha nafasi mpya ya sampuli. Tayari unajua mtoto alitabasamu zaidi ya sekunde nane.

Andika mpya$f(x): f(x) = \frac{1}{23-8} = \frac{1}{15}$

kwa$8 < x < 23$

$P(x > 12 | x > 8) = (23 − 12)\left(\frac{1}{15}\right) = \left(\frac{11}{15}\right)$

Kielelezo$\PageIndex{3}$

Kwa njia ya pili, tumia fomu ya masharti kutoka kwa Mada ya Uwezekano na usambazaji wa awali$X \sim U(0, 23)$:

$P(\text{A|B}) = \frac{P(\text{A AND B})}{P(\text{B})}$

Kwa tatizo hili,$\text{A}$ ni ($x > 12$) na$\text{B}$ ni ($x > 8$).

Hivyo,$P(x > 12|x > 8) = \frac{(x > 12 \text{ AND } x > 8)}{P(x > 8)} = \frac{P(x > 12)}{P(x > 8)} = \frac{\frac{11}{23}}{\frac{15}{23}} = \frac{11}{15}$

Kielelezo$\PageIndex{4}$: Darker kivuli eneo inawakilisha$P(x > 12)$. Nzima kivuli eneo inaonyesha$P(x > 8)$.

Zoezi$\PageIndex{2}$

usambazaji ni kutolewa kama$X \sim U(0, 20)$. Ni nini$P(2 < x < 18)$? Kupata 90 ^th percentile.

Jibu

$P(2 < x < 18) = 0.8$; 90 ^th percentile$= 18$

Mfano 5.3.3

Kiasi cha muda, kwa dakika, kwamba mtu lazima asubiri basi ni sawasawa kusambazwa kati ya sifuri na dakika 15, pamoja.

Zoezi$\PageIndex{3}$.1

a Ni uwezekano gani kwamba mtu anasubiri chini ya dakika 12.5?

Jibu

Hebu idadi$X =$ ya dakika mtu lazima asubiri basi. $a = 0$na$b = 15$. $X \sim U(0, 15)$. Andika kazi ya wiani wa uwezekano. $f(x) = \frac{1}{15-0} = \frac{1}{15}$kwa$0 \leq x \leq 15$.

Kupata$P(x < 12.5)$. Chora grafu.

$$P(x < k) = (\text{base})(\text{height}) = (12.5−0)\left(\frac{1}{15}\right) = 0.8333$$

Uwezekano mtu anasubiri chini ya dakika 12.5 ni 0.8333.

Kielelezo$\PageIndex{5}$.

Zoezi$\PageIndex{3}$.2

b Kwa wastani, mtu lazima asubiri muda gani? Kupata maana,$\mu$, na kupotoka kiwango,$\sigma$.

Jibu

b$\mu = \frac{a+b}{2} = \frac{15+0}{2} = 7.5$. Kwa wastani, mtu lazima asubiri dakika 7.5.

$\sigma = \sqrt{\frac{(b-a)^{2}}{12}} = \sqrt{\frac{(12-0)^{2}}{12}} = 4.3$. Kupotoka kwa kiwango ni dakika 4.3.

Zoezi$\PageIndex{3}$.3

c. asilimia tisini ya muda, wakati mtu lazima kusubiri iko chini ya thamani gani?

Kumbuka 5.3.3.3.1

Hii anauliza kwa asilimia 90 ^th.

Jibu

c Kupata 90 ^th percentile. Chora grafu. Hebu$k =$ 90 ^th percentile.

$P(x < k) = (\text{base})(\text{height}) = (k−0)\left(\frac{1}{15}\right)$
$0.90 = (k)\left(\frac{1}{15}\right)$
$k = (0.90)(15) = 13.5$
$k$wakati mwingine huitwa thamani muhimu.
^{Asilimia ya} 90 ni dakika 13.5. Asilimia tisini ya muda, mtu lazima asubiri dakika 13.5 zaidi.

Kielelezo$\PageIndex{6}$.

Zoezi$\PageIndex{4}$

Muda wa jumla wa michezo ya baseball katika ligi kuu katika msimu wa 2011 unasambazwa kwa usawa kati ya masaa 447 na masaa 521 pamoja.

1. Pata$a$$b$ na ueleze kile wanachowakilisha.
2. Andika usambazaji.
3. Pata maana na kupotoka kwa kiwango.
4. Je! Ni uwezekano gani kwamba muda wa michezo kwa timu ya msimu wa 2011 ni kati ya masaa 480 na 500?
5. ni 65 ^th percentile kwa muda wa michezo kwa ajili ya timu kwa ajili ya msimu 2011?

Jibu

1. $a$ni$447$, na$b$ ni$521$. a ni muda wa chini wa michezo kwa ajili ya timu kwa ajili ya msimu 2011, na$b$ ni muda upeo wa michezo kwa ajili ya timu kwa ajili ya msimu 2011.
2. $X \sim U(447, 521)$.
3. $\mu = 484$, na$\sigma = 21.36$

   

   Kielelezo$\PageIndex{1}$.

4. $P(480 < x < 500) = 0.2703$
5. ^Asilimia 65 ni masaa 495.1.

Mfano 5.3.4

Tuseme wakati inachukua umri wa miaka tisa kula donut ni kati ya dakika 0.5 na 4, pamoja. Hebu$X =$ wakati, kwa dakika, inachukua mtoto mwenye umri wa miaka tisa kula donut. Kisha$X \sim U(0.5, 4)$.

a. uwezekano wa kuwa mtoto mwenye umri wa miaka tisa aliyechaguliwa kwa nasibu anakula donut angalau dakika mbili ni _______.

Suluhisho

a. 0.5714

Zoezi$\PageIndex{4}$.1

pata uwezekano wa kuwa mtoto tofauti mwenye umri wa miaka tisa anakula donut kwa dakika zaidi ya mbili kutokana na kwamba mtoto tayari amekula donut kwa zaidi ya dakika 1.5.

Swali la pili lina uwezekano wa masharti. Unaulizwa kupata uwezekano kwamba mtoto mwenye umri wa miaka tisa anakula donut kwa dakika zaidi ya mbili kutokana na kwamba mtoto tayari amekula donut kwa dakika zaidi ya 1.5. Tatua tatizo njia mbili tofauti (angalia Mfano). Lazima kupunguza nafasi ya sampuli. Njia ya kwanza: Kwa kuwa unajua mtoto tayari amekula donut kwa dakika zaidi ya 1.5, hutaanza tena saa = 0.5 dakika. Hatua yako ya kuanzia ni dakika 1.5.

Andika mpya$f(x)$:

$f(x) = \frac{1}{4-1.5} = \frac{2}{5}$kwa$1.5 \leq x \leq 4$.

Kupata$P(x > 2|x > 1.5)$. Chora grafu.

Kielelezo$\PageIndex{2}$.

$P(x > 2|x > 1.5) = (\text{base})(\text{new height}) = (4 − 2)(25)\left(\frac{2}{5}\right) =$?

Jibu

b.$\frac{4}{5}$

Uwezekano kwamba mtoto mwenye umri wa miaka tisa anakula donut kwa dakika zaidi ya mbili kutokana na kwamba mtoto tayari amekula donut kwa dakika zaidi ya 1.5 ni$\frac{4}{5}$.

Njia ya pili: Chora grafu ya awali kwa$X \sim U(0.5, 4)$. Tumia formula ya masharti

$P(x > 2 | x > 1.5) = \frac{P(x > 2 \text{AND} x > 1.5)}{P(x > 1.5)} = \frac{P(x>2)}{P(x>1.5)} = \frac{\frac{2}{3.5}}{\frac{2.5}{3.5}} = 0.8 = \frac{4}{5}$

Zoezi$\PageIndex{5}$

Tuseme wakati inachukua mwanafunzi kumaliza jaribio ni enhetligt kusambazwa kati ya dakika sita na 15, umoja. Hebu$X =$ wakati, kwa dakika, inachukua mwanafunzi kumaliza jaribio. Kisha$X \sim U(6, 15)$.

Pata uwezekano kwamba mwanafunzi aliyechaguliwa kwa nasibu anahitaji angalau dakika nane ili kukamilisha jaribio. Kisha kupata uwezekano kwamba mwanafunzi tofauti anahitaji angalau dakika nane kumaliza jaribio kutokana na kwamba tayari amechukua dakika zaidi ya saba.

Jibu

$P(x > 8) = 0.7778$

$P(x > 8 | x > 7) = 0.875$

Mfano 5.3.5

Ace Inapokanzwa na Huduma ya Hali ya hewa inaona kwamba kiasi cha muda mtengenezaji anahitaji kurekebisha tanuru ni sawasawa kusambazwa kati ya masaa 1.5 na nne. Hebu$x =$ wakati unahitajika kurekebisha tanuru. Kisha$x \sim U(1.5, 4)$.

1. Pata uwezekano wa kutengeneza tanuru iliyochaguliwa kwa nasibu inahitaji zaidi ya masaa mawili.
2. Pata uwezekano wa kutengeneza tanuru iliyochaguliwa kwa nasibu inahitaji chini ya masaa matatu.
3. Pata asilimia 30 ^ya nyakati za kutengeneza tanuru.
4. Zaidi ya 25% ya nyakati za kutengeneza tanuru huchukua angalau muda gani? (Kwa maneno mengine: kupata muda wa chini kwa muda mrefu zaidi ya 25% ya nyakati za kutengeneza.) Je, hii inawakilisha asilimia gani?
5. Kupata maana na kiwango kupotoka

Suluhisho

a Ili kupata$f(x): f(x) = \frac{1}{4-1.5} = \frac{1}{2.5}$ hivyo$f(x) = 0.4$

$P(x > 2) = (\text{base})(\text{height}) = (4 – 2)(0.4) = 0.8$

Kielelezo$\PageIndex{3}$. Usambazaji wa kawaida kati ya 1.5 na nne na eneo la kivuli kati ya mbili na nne anayewakilisha uwezekano kwamba wakati wa kutengeneza$x$ ni mkubwa kuliko mbili

b.$P(x < 3) = (\text{base})(\text{height}) = (3 – 1.5)(0.4) = 0.6$

Grafu ya mstatili inayoonyesha usambazaji mzima ingebaki sawa. Hata hivyo, grafu inapaswa kuwa kivuli kati$x = 1.5$ na$x = 3$. Kumbuka kuwa eneo la kivuli linaanza$x = 1.5$ badala ya$x = 0$; tangu$X \sim U(1.5, 4)$,$x$ hawezi kuwa chini ya 1.5.

Kielelezo$\PageIndex{4}$. Usambazaji wa kawaida kati ya 1.5 na nne na eneo la kivuli kati ya 1.5 na tatu inayowakilisha uwezekano kwamba wakati wa kutengeneza$x$ ni chini ya tatu

c.

Kielelezo$\PageIndex{5}$. Usambazaji wa kawaida kati ya 1.5 na 4 na eneo la 0.30 kivuli upande wa kushoto, unaowakilisha muda mfupi zaidi wa 30% ya nyakati za kutengeneza.

$P(x < k) = 0.30$
$P(x < k) = (\text{base})(\text{height}) = (k – 1.5)(0.4)$
$0.3 = (k – 1.5) (0.4)$; Tatua kupata$k$:
$0.75 = k – 1.5$, kupatikana kwa kugawanya pande zote mbili na 0.4
$k = 2.25$, kupatikana kwa kuongeza 1.5 kwa pande zote mbili

^Asilimia 30 ya nyakati za kutengeneza ni masaa 2.25. 30% ya nyakati za kutengeneza ni masaa 2.25 au chini.

d.

Kielelezo$\PageIndex{6}$. Usambazaji wa Uniform kati ya 1.5 na 4 na eneo la 0.25 kivuli kwa haki inayowakilisha muda mrefu zaidi wa 25% ya nyakati za kutengeneza.

$P(x > k) = 0.25$
$P(x > k) = (\text{base})(\text{height}) = (4 – k)(0.4)$
$0.25 = (4 – k)(0.4)$; Tatua kwa$k$:
$0.625 = 4 − k$,
kupatikana kwa kugawanya pande zote mbili na 0.4
$−3.375 = −k$,
zilizopatikana kwa kuondoa nne kutoka pande zote mbili: $k = 3.375$
Zaidi ya 25% ya matengenezo ya tanuru huchukua angalau masaa 3.375 (masaa 3.375 au zaidi).

Kumbuka: ^{Tangu 25% ya nyakati za kutengeneza ni masaa 3.375 au zaidi, hiyo ina maana kwamba 75% ya nyakati za kutengeneza ni masaa 3.375 au chini. Masaa 3.375 ni asilimia 75 ya nyakati za kutengeneza tanuru.}

e.$\mu = \frac{a+b}{2}$ na$\sigma = \sqrt{\frac{(b-a)^{2}}{12}}$

$\mu = \frac{1.5+4}{2} = 2.75$masaa na$\sigma = \sqrt{\frac{(4-1.5)^{2}}{12}} = 0.7217$ masaa

Zoezi$\PageIndex{6}$

Kiasi cha muda mtaalamu wa huduma anahitaji kubadilisha mafuta katika gari ni sawasawa kusambazwa kati ya dakika 11 na 21. Hebu$X =$ wakati unahitajika kubadili mafuta kwenye gari.

1. Andika variable random$X$ kwa maneno. $X =$__________________.
2. Andika usambazaji.
3. Graph usambazaji.
4. Kupata$P(x > 19)$.
5. Kupata 50 ^th percentile.

Jibu

1. Hebu$X =$ wakati unahitajika kubadili mafuta katika gari.
2. $X \sim U(11, 21)$.

3. 

   Kielelezo$\PageIndex{7}$.

4. $P(x > 19) = 0.2$
5. 50 ^th percentile ni dakika 16.

Tathmini

Ikiwa$X$ ina usambazaji sare ambapo$a < x < b$ au$a \leq x \leq b$, kisha$X$ inachukua maadili kati$a$ na$b$ (inaweza kujumuisha$a$ na$b$). Maadili yote$x$ ni sawa. Tunaandika$X \sim U(a, b)$. Maana ya$X$ ni$\mu = \frac{a+b}{2}$. kupotoka kiwango cha$X$ ni$\sigma = \sqrt{\frac{(b-a)^{2}}{12}}$. uwezekano wiani kazi ya$X$ ni$f(x) = \frac{1}{b-a}$ kwa ajili ya$a \leq x \leq b$. nyongeza usambazaji kazi ya$X$ ni$P(X \leq x) = \frac{x-a}{b-a}$. $X$ni endelevu.

Kielelezo$\PageIndex{8}$.

uwezekano$P(c < X < d)$ inaweza kupatikana kwa kompyuta eneo chini ya$f(x)$, kati$c$ na$d$. Kwa kuwa eneo linalofanana ni mstatili, eneo hilo linaweza kupatikana tu kwa kuzidisha upana na urefu.

Mapitio ya Mfumo

$X =$idadi halisi kati$a$ na$b$ (katika baadhi ya matukio,$X$ inaweza kuchukua maadili$a$ na$b$). $a =$ndogo$X$;$b =$ kubwa$X$

$X \sim U(a, b)$

Maana ni$\mu = \frac{a+b}{2}$

Kupotoka kwa kiwango ni$\sigma = \sqrt{\frac{(b-a)^{2}}{12}}$

Uwezekano wiani kazi:$f(x) = \frac{1}{b-a} \text{for} a \leq X \leq b$

Eneo kwa upande wa kushoto wa$x$:$P(X < x) = (x – a)\left(\frac{1}{b-a}\right)$

Eneo la Haki ya$x$: P ($X$>$x$) = (b — x)$\left(\frac{1}{b-a}\right)$

Eneo Kati$c$ na$d$:$P(c < x < d) = (\text{base})(\text{height}) = (d – c)\left(\frac{1}{b-a}\right)$

Sare:$X \sim U(a, b)$ wapi$a < x < b$

• pdf:$f(x) = \frac{1}{b-a}$ kwa$a \leq x \leq b$
• cdf:$P(X \leq x) = \frac{x-a}{b-a}$
• maana$\mu = \frac{a+b}{2}$
• kiwango kupotoka$\sigma = \sqrt{\frac{(b-a)^{2}}{12}}$
• $P(c < X < d) = (d – c)\left(\frac{1}{b-a}\right)$

Marejeo

McDougall, John A. McDougall Programu ya Upeo Kupoteza uzito. Plume, 1995.

Tumia maelezo yafuatayo ili kujibu maswali kumi ijayo. Takwimu zinazofuata ni picha za mraba (katika futi 1,000 za mraba) za nyumba 28.

1.5	2.4	3.6	2.6	1.6	2.4	2.0
3.5	2.5	1.8	2.4	2.5	3.5	4.0
2.6	1.6	2.2	1.8	3.8	2.5	1.5
2.8	1.8	4.5	1.9	1.9	3.1	1.6

Sampuli inamaanisha = 2.50 na kupotoka kwa kiwango cha sampuli = 0.8302.

Usambazaji unaweza kuandikwa kama$X \sim U(1.5, 4.5)$.

Zoezi$\PageIndex{7}$

Ni aina gani ya usambazaji huu?

Zoezi$\PageIndex{8}$

Katika usambazaji huu, matokeo yanawezekana sawa. Hii inamaanisha nini?

Jibu

Ina maana kwamba thamani ya x ni kama uwezekano wa kuwa idadi yoyote kati ya 1.5 na 4.5.

Zoezi$\PageIndex{9}$

Je, ni urefu wa$f(x)$ kwa ajili ya usambazaji kuendelea uwezekano?

Zoezi$\PageIndex{10}$

Je, ni vikwazo kwa maadili ya$x$?

Jibu

$1.5 \leq x \leq 4.5$

Zoezi$\PageIndex{11}$

Grafu$P(2 < x < 3)$.

Zoezi$\PageIndex{12}$

Ni nini$P(2 < x < 3)$?

Jibu

0.3333

Zoezi$\PageIndex{13}$

Ni nini$P(x < 3.5 | x < 4)$?

Zoezi$\PageIndex{14}$

Ni nini$P(x = 1.5)$?

Jibu

sufuri

Zoezi$\PageIndex{15}$

Je, ni asilimia 90 ^th ya Footage mraba kwa ajili ya nyumba?

Zoezi$\PageIndex{16}$

Pata uwezekano kwamba nyumba iliyochaguliwa kwa nasibu ina zaidi ya futi za mraba 3,000 kutokana na kwamba tayari unajua nyumba ina zaidi ya miguu ya mraba 2,000.

Jibu

0.6

Zoezi$\PageIndex{17}$

Ni nini$a$? Inawakilisha nini?

Zoezi$\PageIndex{18}$

Ni nini$b$? Inawakilisha nini?

Jibu

$b$ni$12$, na inawakilisha thamani ya juu ya$x$.

Zoezi$\PageIndex{19}$

Je, ni uwezekano wiani kazi gani?

Zoezi$\PageIndex{20}$

Nini maana ya kinadharia?

Jibu

sita

Zoezi$\PageIndex{21}$

Kupotoka kwa kiwango cha kinadharia ni nini?

Zoezi$\PageIndex{22}$

Chora grafu ya usambazaji kwa$P(x > 9)$.

Jibu

Kielelezo$\PageIndex{9}$.

Zoezi$\PageIndex{23}$

Kupata$P(x > 9)$.

Zoezi$\PageIndex{24}$

Kupata 40 ^th percentile.

Jibu

4.8

Tumia maelezo yafuatayo ili kujibu mazoezi kumi na moja ijayo. Umri wa magari katika kura ya maegesho ya wafanyakazi wa chuo cha miji ni sawasawa kusambazwa kutoka miezi sita (miaka 0.5) hadi miaka 9.5.

Zoezi$\PageIndex{25}$

Ni nini kinachopimwa hapa?

Zoezi$\PageIndex{26}$

Kwa maneno, kufafanua variable random$X$.

Jibu

$X$= Umri (katika miaka) ya magari katika kura ya maegesho ya wafanyakazi

Zoezi$\PageIndex{27}$

Je, data ni ya kipekee au inayoendelea?

Zoezi$\PageIndex{28}$

Muda wa maadili kwa$x$ ni ______.

Jibu

0.5 hadi 9.5

Zoezi$\PageIndex{29}$

Usambazaji kwa$X$ ni ______.

Zoezi$\PageIndex{30}$

Andika kazi ya wiani wa uwezekano.

Jibu

$f(x) = \frac{1}{9}$ambapo$x$ ni kati ya 0.5 na 9.5, umoja.

Zoezi$\PageIndex{31}$

Grafu usambazaji uwezekano.

1. Mchoro grafu ya usambazaji wa uwezekano.

   

   Kielelezo$\PageIndex{10}$.

2. Tambua maadili yafuatayo:
   1. Thamani ya chini kabisa kwa$\bar{x}$: _______
   2. Thamani ya juu zaidi kwa$\bar{x}$: _______
   3. Urefu wa mstatili: _______
   4. Lebo ya x -axis (maneno): _______
   5. Lebo kwa y -axis (maneno): _______

Zoezi$\PageIndex{32}$

Kupata umri wa wastani wa magari katika kura.

Jibu

$\mu$= 5

Zoezi$\PageIndex{33}$

Pata uwezekano kwamba gari lililochaguliwa kwa nasibu katika kura lilikuwa chini ya miaka minne.

1. Mchoro grafu, na kivuli eneo la riba.

   

   Kielelezo$\PageIndex{11}$.

2. Kupata uwezekano. $P(x < 4) =$_______

Zoezi$\PageIndex{34}$

Kuzingatia magari tu chini ya umri wa miaka 7.5, pata uwezekano kwamba gari lililochaguliwa kwa nasibu katika kura lilikuwa chini ya miaka minne.

1. Mchoro grafu, kivuli eneo la riba.

   

   Kielelezo$\PageIndex{12}$.

2. Kupata uwezekano. $P(x < 4 | x < 7.5) =$_______

Jibu

1. Angalia ufumbuzi wa mwanafunzi.
2. $\frac{3.5}{7}$

Zoezi$\PageIndex{35}$

Nini kimebadilika katika matatizo mawili yaliyopita ambayo alifanya ufumbuzi tofauti

Zoezi$\PageIndex{36}$

Kupata robo ya tatu ya umri wa magari katika kura. Hii ina maana utakuwa na kupata thamani kama kwamba$\frac{3}{4}$, au 75%, ya magari ni saa zaidi (chini ya au sawa na) umri huo.

1. Mchoro grafu, na kivuli eneo la riba.

   

   Kielelezo$\PageIndex{13}$.

2. Pata thamani$k$ kama hiyo$P(x < k) = 0.75$.
3. Quartile ya tatu ni _______

Jibu

1. Angalia ufumbuzi wa mwanafunzi.
2. $k = 7.25$
3. $7.25$

faharasa

Uwezekano wa masharti

uwezekano kwamba tukio kutokea kutokana na kwamba tukio jingine tayari ilitokea