5.1: Utangulizi

Last updated
Save as PDF

Page ID: 181123

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

SURA YA MALENGO

Mwishoni mwa sura hii, mwanafunzi anapaswa kuwa na uwezo wa:

Kutambua na kuelewa kuendelea uwezekano wiani kazi kwa ujumla.
Tambua usambazaji wa uwezekano wa sare na uitumie ipasavyo.
Kutambua kielelezo uwezekano usambazaji na kuitumia ipasavyo.

Vigezo vya random vinavyoendelea vina programu nyingi. Baseball batting wastani, alama IQ, urefu wa muda mrefu umbali simu wito hudumu, kiasi cha fedha mtu hubeba, urefu wa muda Chip kompyuta huchukua, na SAT alama ni chache tu. Shamba la kuaminika linategemea aina mbalimbali za vigezo vya random.

Maadili ya vigezo vya random visivyofaa na vinavyoendelea vinaweza kuwa na utata. Kwa mfano, ikiwa\(X\) ni sawa na idadi ya maili (kwa maili ya karibu) unaendesha gari kwenda kufanya kazi, basi\(X\) ni kutofautiana kwa random isiyo ya kawaida. Unahesabu maili. Kama\(X\) ni umbali gari kwa kazi, basi kupima maadili ya\(X\) na\(X\) ni kuendelea random variable. Kwa mfano wa pili, ikiwa\(X\) ni sawa na idadi ya vitabu katika mkoba, basi\(X\) ni kutofautiana kwa random isiyo ya kawaida. Kama\(X\) ni uzito wa kitabu, basi\(X\) ni kuendelea random variable kwa sababu uzito ni kipimo. Jinsi variable random hufafanuliwa ni muhimu sana.

Picha inaonyesha mimea ya radish ya urefu mbalimbali inayoongezeka nje ya uchafu. — Kielelezo\(\PageIndex{1}\): urefu wa mimea hii radish ni kuendelea random vigezo. (Mikopo: Rev Stan)

Mali ya Mgawanyiko wa Uwezekano unaoendelea

Grafu ya usambazaji wa uwezekano unaoendelea ni safu. Uwezekano unawakilishwa na eneo chini ya pembe. Curve inaitwa kazi ya wiani wa uwezekano (iliyofupishwa kama pdf). Tunatumia ishara\(f(x)\) ili kuwakilisha safu. \(f(x)\)ni kazi inayofanana na grafu; tunatumia kazi ya wiani\(f(x)\) kuteka grafu ya usambazaji wa uwezekano. Eneo chini ya Curve hutolewa na kazi tofauti inayoitwa kazi ya usambazaji wa nyongeza (iliyofupishwa kama cdf). Kazi ya usambazaji wa jumla hutumiwa kutathmini uwezekano kama eneo.

Matokeo hupimwa, hayakuhesabiwa.
Eneo lote chini ya pembe na juu ya x-axis ni sawa na moja.
Uwezekano hupatikana kwa vipindi vya\(x\) maadili badala ya\(x\) maadili ya mtu binafsi.
\(P(c < x < d)\)ni uwezekano kwamba variable random\(X\) ni katika muda kati ya maadili\(c\) na\(d\). \(P(c < x < d)\)ni eneo chini ya Curve, juu x -axis, na haki ya\(c\) na kushoto ya\(d\).
\(P(x = c) = 0\)Uwezekano\(x\) unaochukua thamani yoyote ya mtu binafsi ni sifuri. Eneo chini ya pembe, juu ya x -axis, na kati\(x = c\) na\(x = c\) haina upana, na kwa hiyo hakuna eneo (eneo = 0). Kwa kuwa uwezekano ni sawa na eneo hilo, uwezekano pia ni sifuri.
\(P(c < x < d)\)ni sawa na uwezekano\(P(c \leq x \leq d)\) kwa sababu ni sawa na eneo hilo.

Tutapata eneo ambalo linawakilisha uwezekano kwa kutumia jiometri, formula, teknolojia, au meza za uwezekano. Kwa ujumla, calculus inahitajika ili kupata eneo chini ya pembe kwa kazi nyingi za wiani wa uwezekano. Tunapotumia fomu ili kupata eneo katika kitabu hiki, fomu zilipatikana kwa kutumia mbinu za calculus muhimu. Hata hivyo, kwa sababu wanafunzi wengi wanaotumia kozi hii hawajasoma calculus, hatuwezi kutumia calculus katika kitabu hiki. Kuna mgawanyo unaoendelea uwezekano. Wakati wa kutumia usambazaji wa uwezekano unaoendelea kwa mfano uwezekano, usambazaji unaotumiwa huchaguliwa kutengeneza na kufaa hali fulani kwa njia bora.

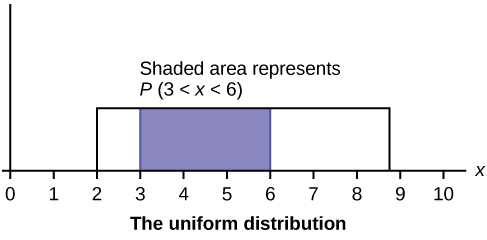
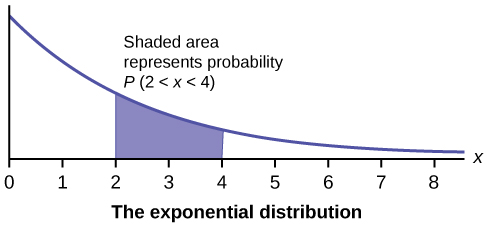
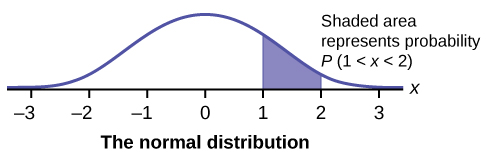
Katika sura hii na ijayo, tutajifunza usambazaji sare, usambazaji wa kielelezo, na usambazaji wa kawaida. Grafu zifuatazo zinaonyesha mgawanyo huu.

Kielelezo\(\PageIndex{2}\): Grafu inaonyesha Distribution Uniform\(x = 3\) na eneo kati na\(x = 6\) kivuli kuwakilisha uwezekano kwamba thamani ya kutofautiana random\(X\) ni katika muda kati ya tatu na sita.

Kielelezo\(\PageIndex{3}\): Grafu inaonyesha Distribution Kielelezo\(x = 2\) na eneo kati na\(x = 4\) kivuli kuwakilisha uwezekano kwamba thamani ya kutofautiana random\(X\) ni katika muda kati ya mbili na nne.

Kielelezo\(\PageIndex{4}\): Grafu inaonyesha Usambazaji wa kawaida wa kawaida na eneo kati\(x = 1\) na\(x = 2\) kivuli ili kuwakilisha uwezekano kwamba thamani ya kutofautiana kwa random\(X\) iko katika muda kati ya moja na mbili.

faharasa

Usambazaji Sare: kuendelea random variable (RV) ambayo ina matokeo sawa uwezekano juu ya uwanja,\(a < x < b\); mara nyingi hujulikana kama usambazaji mstatili kwa sababu graph ya pdf ina aina ya mstatili. Nukuu:\(X \sim U(a,b)\). Maana ni\(\mu = \frac{a+b}{2}\) na kupotoka kwa kiwango ni\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\). Kazi ya wiani ya uwezekano ni\(f(x) = \frac{1}{b-a}\) kwa\(a < x < b\) au\(a \leq x \leq b\). Usambazaji wa jumla ni\(P(X \leq x) = \frac{x-a}{b-a}\).

Usambazaji wa kielelezo: kuendelea random variable (RV) kwamba inaonekana wakati sisi ni nia ya vipindi vya muda kati ya baadhi ya matukio random, kwa mfano, urefu wa muda kati ya waliofika dharura katika hospitali; nukuu ni\(X \sim \text{Exp}(m)\). Maana ni\(\mu = \frac{1}{m}\) na kupotoka kwa kiwango ni\(\sigma = \frac{1}{m}\). uwezekano wiani kazi ni\(f(x) = me^{-mx}\),\(x \geq 0\) na nyongeza usambazaji kazi ni\(P(X \leq x) = 1 − e^{mx}\).