7.1: Idadi ya busara na isiyo ya kawaida
- Page ID
- 173313
- Tambua namba za busara na namba zisizo na maana
- Kuainisha aina tofauti za idadi halisi
Kabla ya kuanza, fanya jaribio hili la utayari.
- Andika 3.19 kama sehemu isiyofaa. Ikiwa umekosa tatizo hili, kagua Mfano 5.1.4.
- Andika\(\dfrac{5}{11}\) kama decimal. Ikiwa umekosa tatizo hili, kagua Mfano 5.5.3.
- Kurahisisha:\(\sqrt{144}\). Ikiwa umekosa tatizo hili, kagua Mfano 5.12.1.
Tambua Hesabu za busara na Hesabu zisizofaa
Hongera! Umemaliza sura sita za kwanza za kitabu hiki! Ni wakati wa kuchukua hisa ya kile ulichofanya hadi sasa katika kozi hii na kufikiri juu ya kile kilicho mbele. Umejifunza jinsi ya kuongeza, kuondoa, kuzidisha, na kugawanya idadi nzima, sehemu ndogo, integers, na decimals. Umekuwa ukoo na lugha na alama ya algebra, na kuwa rahisi na tathmini maneno algebraic. Umefanya kutatuliwa aina nyingi za programu. Umeanzisha msingi mzuri ambao unahitaji ili uweze kufanikiwa katika algebra.
Katika sura hii, tutahakikisha ujuzi wako umewekwa imara. Tutaweza kuangalia mwingine aina ya idadi tumefanya kazi na katika sura zote zilizopita. Tutafanya kazi na mali ya namba ambazo zitakusaidia kuboresha hisia yako ya nambari. Na tutaweza mazoezi ya kutumia yao katika njia ambazo tutaweza kutumia wakati sisi kutatua milinganyo na kukamilisha taratibu nyingine katika algebra.
Tayari tumeelezea namba kama namba za kuhesabu, namba nzima, na integers. Je! Unakumbuka ni tofauti gani kati ya aina hizi za namba?
| kuhesabu idadi | 1, 2, 3, 4... |
| idadi nzima | 0, 1, 2, 3, 4... |
| namba kamili | ... —3, -2, -1, 0, 1, 2, 3, 4... |
Idadi ya busara
Ni aina gani ya namba ungepata ikiwa ulianza na integers zote na kisha umejumuisha sehemu zote? Nambari ungependa kuunda seti ya namba za busara. Nambari ya busara ni namba ambayo inaweza kuandikwa kama uwiano wa integers mbili.
Nambari ya busara ni namba ambayo inaweza kuandikwa kwa fomu\(\dfrac{p}{q}\), ambapo p na q ni integers na q 合 0.
Sehemu zote, zote nzuri na hasi, ni namba za busara. Mifano michache ni
\[\dfrac{4}{5}, - \dfrac{7}{8}, \dfrac{13}{4},\; and\; - \dfrac{20}{3}\]
Kila nambari na kila denominator ni integer.
Tunahitaji kuangalia namba zote ambazo tumezitumia hadi sasa na kuthibitisha kuwa ni busara. Ufafanuzi wa namba za busara hutuambia kwamba sehemu zote ni za busara. Sasa tutaangalia namba za kuhesabu, namba nzima, integers, na decimals ili kuhakikisha kuwa ni busara.
Ni namba integers busara? Kuamua kama integer ni namba ya busara, tunajaribu kuandika kama uwiano wa integers mbili. Njia rahisi ya kufanya hivyo ni kuandika kama sehemu na denominator moja.
\[3 = \dfrac{3}{1} \quad -8 = \dfrac{-8}{1} \quad 0 = \dfrac{0}{1}\]
Kwa kuwa integer yoyote inaweza kuandikwa kama uwiano wa integers mbili, integers zote ni namba za busara. Kumbuka kwamba namba zote za kuhesabu na namba zote pia ni integers, na hivyo wao, pia, ni busara.
Nini kuhusu decimals? Je, wao ni busara? Hebu tuangalie wachache kuona kama tunaweza kuandika kila mmoja wao kama uwiano wa integers mbili. Tumeona kwamba integers ni namba za busara. Nambari integer -8 inaweza kuandikwa kama decimal -8.0. Kwa hiyo, kwa wazi, baadhi ya decimals ni busara.
Fikiria juu ya decimal 7.3. Je, tunaweza kuandika kama uwiano wa integers mbili? Kwa sababu 7.3 inamaanisha\(7 \dfrac{3}{10}\), tunaweza kuandika kama sehemu isiyofaa,\(7 \dfrac{3}{10}\). Hivyo 7.3 ni uwiano wa integers 73 na 10. Ni idadi ya busara.
Kwa ujumla, decimal yoyote inayoishia baada ya tarakimu kadhaa (kama vile 7.3 au -1.2684) ni namba ya busara. Tunaweza kutumia requipral (au multiplicative inverse) ya thamani ya mahali ya tarakimu ya mwisho kama denominator wakati wa kuandika decimal kama sehemu.
Andika kila mmoja kama uwiano wa integers mbili: (a) -15 (b) 6.81 (c)\(−3 \dfrac{6}{7}\).
Suluhisho
(a) -15
| Andika integer kama sehemu na denominator 1. | $$\ dfrac {-15} {1} $$ |
(b) 6.81
| Andika decimal kama nambari iliyochanganywa. | $6\ dfrac {81} {100} $$ |
| Kisha ubadilishe kwa sehemu isiyofaa. | $$\ dfrac {681} {100} $$ |
(c)\(−3 \dfrac{6}{7}\)
| Badilisha nambari iliyochanganywa kwa sehemu isiyofaa. | $$-\ dfrac {27} {7} $$ |
Andika kila mmoja kama uwiano wa integers mbili: (a) -24 (b) 3.57.
- Jibu
-
\(\frac{-24}{1}\)
- Jibu b
-
\(\frac{357}{100}\)
Andika kila mmoja kama uwiano wa integers mbili: (a) -19 (b) 8.41.
- Jibu
-
\(\frac{-19}{1}\)
- Jibu b
-
\(\frac{841}{100}\)
Hebu tuangalie fomu ya decimal ya namba tunayojua ni ya busara. Tumeona kwamba kila integer ni idadi ya busara, tangu =\(\dfrac{a}{1}\) kwa integer yoyote, a Tunaweza pia kubadilisha integer yoyote kwa decimal kwa kuongeza uhakika decimal na sifuri.
\[\begin{split} Integer \qquad &-2,\quad -1,\quad 0,\quad 1,\; \; 2,\; 3 \\ Decimal \qquad &-2.0, -1.0, 0.0, 1.0, 2.0, 3.0 \end{split}\]
Nambari hizi za decimal zinaacha.
Tumeona pia kwamba kila sehemu ni idadi ya busara. Angalia fomu ya decimal ya vipande ambavyo tulizingatia tu.
\[\begin{split} Ratio\; of\; Integers \qquad \dfrac{4}{5},\quad -\dfrac{7}{8},\quad \dfrac{13}{4},\;&- \dfrac{20}{3} \\ Decimal\; forms \qquad 0.8, -0.875, 3.25, &-6.666 \ldots \\ &-6.\overline{66} \end{split}\]
Hizi decimals ama kuacha au kurudia.
Mifano hii inakuambia nini? Kila nambari ya busara inaweza kuandikwa wote kama uwiano wa integers na kama decimal ambayo inaacha au kurudia. Jedwali hapa chini linaonyesha namba ambazo tumeangalia zilionyesha kama uwiano wa integers na kama decimal.
| Idadi ya busara | ||
|---|---|---|
| FRACTIONS | Nambari kamili | |
| Idadi | $$\ dfrac {4} {5}, -\ dfrac {7} {8},\ dfrac {13} {4},\ dfrac {-20} {3} $$ | $-2, -1, 0, 1, 2, 3 $$ |
| Uwiano wa Integer | $$\ dfrac {4} {5},\ dfrac {-7} {8},\ dfrac {13} {4},\ dfrac {-20} {3} $$ | $$\ dfrac {-2} {1},\ dfrac {-1} {1},\ dfrac {0} {1},\ dfrac {1},\ dfrac {1},\ dfrac {1},\ dfrac {3} {1} $$ |
| Idadi ya decimal | $0.8, -0.875, 3.25, -6. \ overline {6} $$ | $-2.0, -1.0, 0.0, 1.0, 2.0, 3.0 $$ |
Idadi irrational
Je, kuna decimals yoyote ambayo haina kuacha au kurudia? Ndiyo. Nambari\(\pi\) (herufi ya Kigiriki pi, inayojulikana 'pie'), ambayo ni muhimu sana katika kuelezea miduara, ina fomu ya decimal ambayo haina kuacha wala kurudia.
\[\pi = 3.141592654 \ldots \ldots\]
Vile vile, uwakilishi wa decimal wa mizizi ya mraba ya idadi nzima ambayo si mraba kamili kamwe kuacha na kamwe kurudia. Kwa mfano,
\[\sqrt{5} = 2.236067978 \ldots \ldots\]
Decimal ambayo haina kuacha na haina kurudia haiwezi kuandikwa kama uwiano wa integers. Tunaita aina hii ya namba namba isiyo na maana.
Nambari isiyo na maana ni namba ambayo haiwezi kuandikwa kama uwiano wa integers mbili. Fomu yake ya decimal haina kuacha na haina kurudia.
Hebu tufanye muhtasari njia tunayoweza kutumia ili kuamua kama namba ni ya busara au isiyo ya maana.
Kama fomu decimal ya idadi
- ataacha au kurudia, idadi ni ya busara.
- haina kuacha na haina kurudia, idadi ni irrational.
Tambua kila moja ya yafuatayo kama ya busara au isiyo ya maana:\(\overline{3}\) (a) 0.58 (b) 0.475 (c) 3.605551275...
Suluhisho
(a) 0.58\(\overline{3}\)
Bar juu ya 3 inaonyesha kwamba inarudia. Kwa hiyo, 0.583 — ni decimal kurudia, na kwa hiyo ni idadi ya busara.
(b) 0.475
Decimal hii inacha baada ya 5, hivyo ni namba ya busara.
(c) 3.605551275...
ellipsis (...) ina maana kwamba nambari hii haina kuacha. Hakuna muundo wa kurudia wa tarakimu. Kwa kuwa idadi haina kuacha na haina kurudia, ni irrational.
Tambua kila moja ya yafuatayo kama ya busara au isiyo ya maana: (a) 0.29 (b) 0.81\(\overline{6}\) (c) 2.515115111...
- Jibu
-
busara
- Jibu b
-
busara
- Jibu c
-
isiyo na maana
Tambua kila moja ya yafuatayo kama ya busara au isiyo ya maana:\(\overline{3}\) (a) 0.2 (b) 0.125 (c) 0.418302...
- Jibu
-
busara
- Jibu b
-
busara
- Jibu c
-
isiyo na maana
Hebu fikiria juu ya mizizi ya mraba sasa. Mizizi ya mraba ya mraba kamilifu daima ni namba nzima, hivyo ni busara. Lakini aina ya decimal ya mizizi ya mraba ya idadi ambayo si mraba kamili kamwe kuacha na kamwe kurudia, hivyo mizizi hii ya mraba ni irrational.
Tambua kila moja ya yafuatayo kama ya busara au isiyo ya maana: (a) 36 (b) 44
Suluhisho
(a) Nambari 36 ni mraba kamili, tangu 6 2 = 36. Hivyo\(\sqrt{36}\) = 6. Kwa hiyo\(\sqrt{36}\) ni busara.
(b) Kumbuka kwamba 6 2 = 36 na 7 2 = 49, hivyo 44 si mraba kamilifu. Hii ina maana\(\sqrt{44}\) ni irrational.
Tambua kila moja ya yafuatayo kama ya busara au isiyo ya maana: (a)\(\sqrt{81}\) (b)\(\sqrt{17}\)
- Jibu
-
busara
- Jibu b
-
isiyo na maana
Tambua kila moja ya yafuatayo kama ya busara au isiyo ya maana: (a)\(\sqrt{116}\) (b)\(\sqrt{121}\)
- Jibu
-
isiyo na maana
- Jibu b
-
busara
Kuainisha Hesabu halisi
Tumeona kwamba namba zote za kuhesabu ni namba nzima, namba zote ni integers, na integers zote ni namba za busara. Nambari zisizo na maana ni jamii tofauti ya wao wenyewe. Tunapoweka namba za busara na namba zisizo na maana, tunapata seti ya namba halisi. Kielelezo\(\PageIndex{1}\) unaeleza jinsi seti idadi ni kuhusiana.
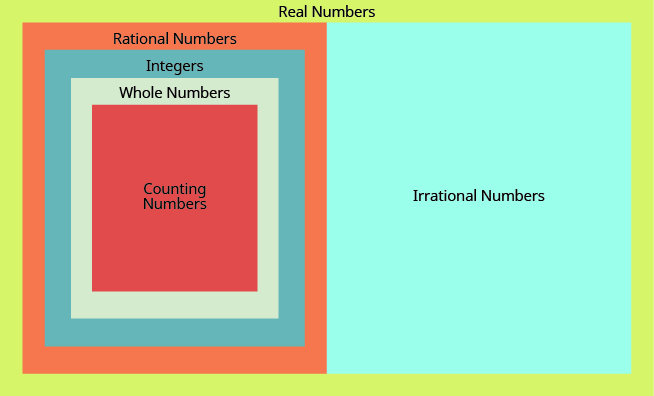
Kielelezo\(\PageIndex{1}\) - Mchoro huu unaeleza mahusiano kati ya aina tofauti za idadi halisi.
Nambari halisi ni namba ambazo ni za busara au zisizo na maana.
Je! Neno “namba halisi” linaonekana kuwa la ajabu kwako? Je, kuna idadi yoyote ambayo si “halisi”, na, ikiwa ni hivyo, inaweza kuwa nini? Kwa karne nyingi, idadi tu watu walijua kuhusu ni nini sisi sasa wito idadi halisi. Kisha wanahisabati waligundua seti ya namba za kufikirika. Huwezi kukutana na idadi imaginary katika kozi hii, lakini utakuwa baadaye katika masomo yako ya algebra.
Kuamua kama kila moja ya idadi katika orodha ifuatayo ni (a) idadi nzima, (b) integer, (c) idadi ya busara, (d) idadi irrational, na (e) idadi halisi.
\[−7, \dfrac{14}{5}, 8, \sqrt{5}, 5.9, − \sqrt{64}\]
Suluhisho
- Nambari nzima ni 0, 1, 2, 3,... namba 8 ni namba nzima pekee iliyotolewa.
- Integers ni namba nzima, kinyume chake, na 0. Kutoka namba zilizotolewa, -7 na 8 ni integers. Pia, angalia kwamba 64 ni mraba wa 8 hivyo\(− \sqrt{64}\) = -8. Hivyo integers ni -7, 8,\(− \sqrt{64}\).
- Kwa kuwa integers zote ni busara, namba -7, 8, na pia\(− \sqrt{64}\) ni busara. Nambari za busara pia zinajumuisha sehemu ndogo na decimals ambazo zinakomesha au kurudia, hivyo\(\dfrac{14}{5}\) na 5.9 ni busara.
- Nambari ya 5 sio mraba kamilifu, hivyo\(\sqrt{5}\) haifai.
- Nambari zote zilizoorodheshwa ni halisi.
Tutaweza muhtasari matokeo katika meza.
| Idadi | Whole | Nambari kamili | Mantiki | Irrational | Real |
|---|---|---|---|---|---|
| -7 | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | ||
| \(\dfrac{14}{5}\) | \(\checkmark\) | \(\checkmark\) | |||
| 8 | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | |
| \(\sqrt{5}\) | \(\checkmark\) | \(\checkmark\) | |||
| 5.9 | \(\checkmark\) | \(\checkmark\) | |||
| \(- \sqrt{64}\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) |
Kuamua kama kila namba ni (a) namba nzima, (b) integer, (c) nambari ya busara, (d) nambari isiyo ya kawaida, na (e) idadi halisi: -3\(− \sqrt{2}, 0.\overline{3}, \dfrac{9}{5}\),, 4,\(\sqrt{49}\).
- Jibu
-
Idadi Whole Nambari kamili Mantiki Irrational Real -3 \(\checkmark\) \(\checkmark\) \(\checkmark\) \(-\sqrt{2}\) \(\checkmark\) \(\checkmark\) \(0.\overline{3}\) \(\checkmark\) \(\checkmark\) \(\dfrac{9}{5}\) \(\checkmark\) \(\checkmark\) \(4\) \(\checkmark\) \(\checkmark\) \(\checkmark\) \(\checkmark\) \(\sqrt{49}\) \(\checkmark\) \(\checkmark\) \(\checkmark\) \(\checkmark\)
Kuamua kama kila idadi ni (a) idadi nzima, (b) integer, (c) idadi ya busara, (d) idadi irrational, na (e) idadi halisi:\(− \sqrt{25}, − \dfrac{3}{8}\), -1, 6\(\sqrt{121}\), 2.041975...
- Jibu
-
Idadi Whole Nambari kamili Mantiki Irrational Real \(− \sqrt{25}\) \(\checkmark\) \(\checkmark\) \(\checkmark\) \(-\dfrac{3}{8}\) \(\checkmark\) \(\checkmark\) \(-1\) \(\checkmark\) \(\checkmark\) \(\checkmark\) \(6\) \(\checkmark\) \(\checkmark\) \(\checkmark\) \(\checkmark\) \(\sqrt{121}\) \(\checkmark\) \(\checkmark\) \(\checkmark\) \(\checkmark\) \(2.041975…\) \(\checkmark\) \(\checkmark\)
Mazoezi hufanya kamili
Idadi ya busara
Katika mazoezi yafuatayo, andika kama uwiano wa integers mbili.
- (a) 5 (b) 3.19
- (a) 8 (b) -1.61
- (a) -12 (b) 9.279
- (a) -16 (b) 4.399
Katika mazoezi yafuatayo, tambua ni nani kati ya nambari zilizopewa ni za busara na ambazo hazina maana.
- 0.75, 0.22\(\overline{3}\), 1.39174...
- 0.36, 0.94729..., 2.52\(\overline{8}\)
- 0. \(\overline{45}\), 1.919293..., 3.59
- 0.1\(\overline{3}\), 0.42982..., 1.875
Katika mazoezi yafuatayo, tambua kama kila nambari ni ya busara au isiyo ya maana.
- (a) 25 (b) 30
- (a) 44 (b) 49
- (a) 164 (b) 169
- (a) 225 (b) 216
Kuainisha Hesabu halisi
Katika mazoezi yafuatayo, onyesha kama kila namba ni nzima, integer, busara, irrational, na halisi.
- -8, 0, 1.95286...\(\dfrac{12}{5}, \sqrt{36}\), 9
- -9\(−3 \dfrac{4}{9}, − \sqrt{9}, 0.4\overline{09}, \dfrac{11}{6}\), 7
- \(− \sqrt{100}\), -7\(− \dfrac{8}{3}\), -1, 0.77,\(3 \dfrac{1}{4}\)
kila siku Math
- Safari ya shamba Wafanyabiashara wote wa 5 katika Shule ya Elementary ya Lincoln watakwenda safari ya shamba kwenda kwenye makumbusho Kuhesabu watoto wote, walimu, na washirika, kutakuwa na watu 147. Kila basi inashikilia watu 44.
- Ni mabasi ngapi yatahitajika?
- Kwa nini jibu lazima liwe namba nzima?
- Kwa nini usizunguze jibu kwa njia ya kawaida?
- Huduma ya watoto Serena anataka kufungua kituo cha huduma ya watoto leseni. Hali yake inahitaji kuwa hakuna watoto zaidi ya 12 kwa kila mwalimu. Angependa kituo cha huduma ya mtoto wake kutumikia watoto 40.
- Ni walimu wangapi watahitajika?
- Kwa nini jibu lazima liwe namba nzima?
- Kwa nini usizunguze jibu kwa njia ya kawaida?
Mazoezi ya kuandika
- Kwa maneno yako mwenyewe, kuelezea tofauti kati ya nambari ya busara na nambari isiyo na maana.
- Eleza jinsi seti ya namba (kuhesabu, nzima, integer, busara, irrationals, reals) zinahusiana na kila mmoja.
Self Check
(a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

(b) Kama wengi wa hundi yako walikuwa:
... kwa ujasiri. Hongera! Umefanikiwa malengo katika sehemu hii. Fikiria ujuzi wa kujifunza uliyotumia ili uweze kuendelea kuitumia. Ulifanya nini ili uwe na ujasiri wa uwezo wako wa kufanya mambo haya? Kuwa maalum.
... kwa msaada fulani. Hii lazima kushughulikiwa haraka kwa sababu mada huna bwana kuwa mashimo katika barabara yako ya mafanikio. Katika hesabu, kila mada hujenga juu ya kazi ya awali. Ni muhimu kuhakikisha kuwa na msingi imara kabla ya kuendelea. Nani unaweza kuomba msaada? Washiriki wenzako na mwalimu ni rasilimali nzuri. Je, kuna mahali kwenye chuo ambapo waalimu hisabati zinapatikana? Je, ujuzi wako wa kujifunza unaweza kuboreshwa?
... hakuna-siipati! Hii ni ishara ya onyo na haipaswi kupuuza. Unapaswa kupata msaada mara moja au utazidiwa haraka. Angalia mwalimu wako haraka iwezekanavyo kujadili hali yako. Pamoja unaweza kuja na mpango wa kupata msaada unayohitaji.


