Home
Kiswahili
Kitabu: Prealgebra (OpenStax)
4: FRACTIONS
4.8: Kuongeza na Ondoa sehemu na Denominators tofauti (Sehemu ya 1)

4.8: Kuongeza na Ondoa sehemu na Denominators tofauti (Sehemu ya 1)

Last updated
Save as PDF

Page ID: 173393

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Kupata denominator angalau kawaida (LCD)
Badilisha FRACTIONS kwa FRACTIONS sawa na LCD
Ongeza na uondoe sehemu ndogo na madhehebu tofauti
Tambua na utumie shughuli za sehemu
Tumia utaratibu wa shughuli ili kurahisisha sehemu ndogo
Tathmini maneno ya kutofautiana na sehemu ndogo

kuwa tayari!

Kabla ya kuanza, fanya jaribio hili la utayari.

Kupata sehemu mbili sawa na$\dfrac{5}{6}$. Kama amekosa tatizo hili, mapitio Mfano 4.1.14.
Kurahisisha:$\dfrac{1 + 5 \cdot 3}{2^{2} + 4}$. Kama amekosa tatizo hili, mapitio Mfano 4.3.13.

Pata Denominator ya kawaida

Katika sehemu iliyopita, tulielezea jinsi ya kuongeza na kuondoa sehemu ndogo na denominator ya kawaida. Lakini tunawezaje kuongeza na kuondoa sehemu ndogo na denominators tofauti?

Hebu fikiria kuhusu sarafu tena. Je, unaweza kuongeza robo moja na dime moja? Unaweza kusema kuna sarafu mbili, lakini hiyo si muhimu sana. Ili kupata thamani ya jumla ya robo moja pamoja na dime moja, unawabadilisha kwa aina moja ya kitengo cha senti. Robo moja ni sawa na$25$ senti na dime moja ni sawa na$10$ senti, hivyo jumla ni$35$ senti. Angalia Kielelezo$\PageIndex{1}$.

$Robo na dime huonyeshwa. Chini yao, inasoma senti 25 pamoja na senti 10. Chini ya hayo, inasoma senti 35.$

Kielelezo$\PageIndex{1}$: Pamoja, robo na dime zina thamani ya senti 35, au$\dfrac{35}{100}$ ya dola.

Vile vile, tunapoongeza sehemu ndogo na denominators tofauti tunapaswa kuzibadilisha kwa sehemu sawa na denominator ya kawaida. Pamoja na sarafu, wakati sisi kubadilisha kwa senti, denominator ni$100$. Kwa kuwa kuna$100$ senti katika dola moja,$25$ senti ni$\dfrac{25}{100}$ na$10$ senti ni$\dfrac{10}{100}$. Hivyo sisi kuongeza$\dfrac{25}{100} + \dfrac{10}{100}$ kupata$\dfrac{35}{100}$, ambayo ni$35$ senti.

Umefanya mazoezi ya kuongeza na kuondoa sehemu ndogo na madhehebu ya kawaida. Sasa hebu tuone unachohitaji kufanya na sehemu ndogo ambazo zina denominators tofauti.

Kwanza, tutatumia tiles sehemu kwa mfano kutafuta denominator ya kawaida ya$\dfrac{1}{2}$ na$\dfrac{1}{3}$. Tutaanza na$\dfrac{1}{2}$ tile moja na$\dfrac{1}{3}$ tile. Tunataka kupata kawaida sehemu tile kwamba tunaweza kutumia kwa mechi zote mbili$\dfrac{1}{2}$ na$\dfrac{1}{3}$ hasa. Kama sisi kujaribu$\dfrac{1}{4}$ vipande,$2$ wao hasa mechi$\dfrac{1}{2}$ kipande, lakini hawana hasa mechi$\dfrac{1}{3}$ kipande.

$Mstatili miwili huonyeshwa kwa upande. Ya kwanza inaitwa nusu 1. Ya pili ni fupi na imeandikwa 1 ya tatu. Chini ya mstatili wa kwanza ni mstatili sawa ukubwa mgawanyiko wima katika vipande viwili, kila kinachoitwa 1 nne. Chini ya mstatili wa pili ni vipande viwili, kila kinachoitwa 1 nne. Hizi rectangles pamoja ni mrefu kuliko mstatili kinachoitwa kama 1 ya tatu.$

Kielelezo$\PageIndex{2}$

Ikiwa tunajaribu$\dfrac{1}{5}$ vipande, hazifunika$\dfrac{1}{2}$ kipande au$\dfrac{1}{3}$ kipande.

$Mstatili miwili huonyeshwa kwa upande. Ya kwanza inaitwa nusu 1. Ya pili ni fupi na imeandikwa 1 ya tatu. Chini ya mstatili wa kwanza ni rectangles tatu ndogo, kila kinachoitwa 1 tano. Pamoja, rectangles hizi ni ndefu kuliko mstatili wa nusu ya 1. Chini ya mstatili wa tatu wa 1 ni rectangles mbili ndogo, kila kinachoitwa 1 tano. Pamoja, rectangles hizi ni ndefu kuliko mstatili wa tatu wa 1.$

Kielelezo$\PageIndex{3}$

Kama tungekuwa kujaribu$\dfrac{1}{12}$ vipande, wangeweza pia kazi.

$Mstatili miwili huonyeshwa kwa upande. Ya kwanza inaitwa nusu 1. Ya pili ni fupi na imeandikwa 1 ya tatu. Chini ya mstatili wa kwanza ni mstatili sawa ukubwa mgawanyiko wima katika vipande 6, kila kinachoitwa 1 kumi na mbili. Chini ya mstatili wa pili ni mstatili sawa ukubwa mgawanyiko wima katika vipande 4, kila kinachoitwa 1 kumi na mbili.$

Kielelezo$\PageIndex{4}$

Hata tiles ndogo, kama vile$\dfrac{1}{24}$ na$\dfrac{1}{48}$, ingekuwa pia hasa kufunika$\dfrac{1}{2}$ kipande na$\dfrac{1}{3}$ kipande. Denominator ya kipande kikubwa zaidi kinachofunika sehemu zote mbili ni denominator ya kawaida (LCD) ya sehemu mbili. Hivyo, angalau kawaida denominator ya$\dfrac{1}{2}$ na$\dfrac{1}{3}$ ni$6$.

Kumbuka kwamba wote wa vigae kwamba kufunika$\dfrac{1}{2}$ na$\dfrac{1}{3}$ kuwa na kitu kwa pamoja: denominators yao ni mafungu ya kawaida ya$2$ na$3$, denominators ya$\dfrac{1}{2}$ na$\dfrac{1}{3}$. angalau ya kawaida nyingi (LCM) ya denominators ni$6$, na hivyo tunasema kwamba$6$ ni denominator angalau kawaida (LCD) ya sehemu ndogo$\dfrac{1}{2}$ na$\dfrac{1}{3}$.

Ufafanuzi: Denominator ya kawaida

Denominator ya kawaida (LCD) ya sehemu mbili ni ndogo zaidi ya kawaida (LCM) ya denominators yao.

Ili kupata LCD ya vipande viwili, tutapata LCM ya denominators yao. Tunafuata utaratibu tuliotumia mapema ili kupata LCM ya namba mbili. Tunatumia tu denominators ya sehemu ndogo, sio nambari, wakati wa kutafuta LCD.

Mfano$\PageIndex{1}$: lcd

Kupata LCD kwa FRACTIONS$\dfrac{7}{12}$ na$\dfrac{5}{18}$.

Suluhisho

Factor kila denominator katika primes yake.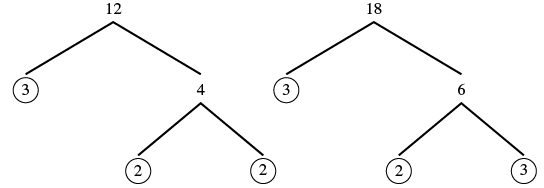
Orodha ya primes ya 12 na primes ya 18 kuifunga yao katika nguzo iwezekanavyo.
Kuleta chini nguzo.
Kuzidisha mambo. Bidhaa ni LCM.	LCM = 36
LCM ya 12 na 18 ni 36, hivyo LCD ya$\dfrac{7}{12}$ na$\dfrac{5}{18}$ ni 36.	LCD ya$\dfrac{7}{12}$ na$\dfrac{5}{18}$ ni 36.

Zoezi$\PageIndex{1}$

Kupata denominator angalau kawaida kwa FRACTIONS:$\dfrac{7}{12}$ na$\dfrac{11}{15}$.

Jibu: $60$

Zoezi$\PageIndex{2}$

Kupata denominator angalau kawaida kwa FRACTIONS:$\dfrac{13}{15}$ na$\dfrac{17}{5}$.

Jibu: $15$

Ili kupata LCD ya vipande viwili, pata LCM ya madhehebu yao. Angalia jinsi hatua zilizoonyeshwa hapa chini zinafanana na hatua tulizochukua ili kupata LCM.

JINSI YA: KUPATA DENOMINATOR ANGALAU YA KAWAIDA (LCD) YA SEHEMU MBILI

Hatua ya 1. Factor kila denominator katika primes yake.

Hatua ya 2. Orodha primes, vinavyolingana primes katika nguzo wakati iwezekanavyo.

Hatua ya 3. Kuleta chini nguzo.

Hatua ya 4. Kuzidisha mambo. Bidhaa hiyo ni LCM ya denominators.

Hatua ya 5. LCM ya denominators ni LCD ya sehemu ndogo.

Mfano$\PageIndex{2}$:

Kupata denominator angalau kawaida kwa FRACTIONS$\dfrac{8}{15}$ na$\dfrac{11}{24}$.

Suluhisho

Ili kupata LCD, tunapata LCM ya denominators. Kupata LCM ya$15$ na$24$.

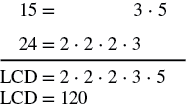
$Mstari wa juu unaonyesha 15 sawa mara 3 5. Mstari unaofuata unaonyesha 24 sawa mara 2 mara 2 mara 3. Ya 3s imefungwa kwa wima. Mstari unaofuata unaonyesha LCM sawa mara 2 mara 2 mara 3 mara 5. Mstari wa mwisho unaonyesha LCM sawa 120.$

LCM ya$15$ na$24$ ni$120$. Hivyo, LCD ya$\dfrac{8}{15}$ na$\dfrac{11}{24}$ ni$120$.

Zoezi$\PageIndex{3}$

Kupata denominator angalau kawaida kwa FRACTIONS:$\dfrac{13}{24}$ na$\dfrac{17}{32}$.

Jibu: $96$

Zoezi$\PageIndex{4}$

Kupata denominator angalau kawaida kwa FRACTIONS:$\dfrac{9}{28}$ na$\dfrac{21}{32}$.

Jibu: $224$

Badilisha FRACTIONS kwa FRACTIONS sawa na LCD

Mapema, tulitumia sehemu tiles kuona kwamba LCD ya$\dfrac{1}{4}$ na$\dfrac{1}{6}$ ni$12$. Tuliona kwamba$\dfrac{1}{12}$ vipande vitatu hasa kufunikwa$\dfrac{1}{4}$ na$\dfrac{1}{12}$ vipande viwili hasa kufunikwa$\dfrac{1}{6}$, hivyo

\[\dfrac{1}{4} = \dfrac{3}{12} \quad and \quad \dfrac{1}{6} = \dfrac{2}{12} \ldotp \nonumber \]

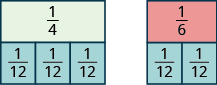
$Kwenye upande wa kushoto ni mstatili unaoitwa 1 nne. Chini ni mstatili unaofanana umegawanyika kwa wima katika vipande 3 sawa, kila kinachoitwa 1 kumi na mbili. Kwenye haki ni mstatili unaoitwa 1 sita. Chini ni mstatili unaofanana umegawanyika kwa wima katika vipande 2 sawa, kila kinachoitwa 1 kumi na mbili.$

Tunasema kwamba$\dfrac{1}{4}$ na$\dfrac{3}{12}$ ni sawa FRACTIONS na pia kwamba$\dfrac{1}{6}$ na$\dfrac{2}{12}$ ni sawa sehemu ndogo.

Tunaweza kutumia Mali sawa Fractions kwa algebraically kubadilisha sehemu kwa moja sawa. Kumbuka, sehemu mbili ni sawa ikiwa zina thamani sawa. Sawa Fractions Mali ni mara kwa mara chini kwa ajili ya kumbukumbu.

Ufafanuzi: Sawa Fractions Mali

Ikiwa$a, b, c$ ni namba nzima ambapo$b ≠ 0$$c ≠ 0$, basi

\[\dfrac{a}{b} = \dfrac{a \cdot c}{b \cdot c} \quad and \quad \dfrac{a \cdot c}{b \cdot c} = \dfrac{a}{b}\]

Ili kuongeza au kuondoa sehemu ndogo na denominators tofauti, tutahitaji kwanza kubadili kila sehemu kwa sehemu sawa na LCD. Hebu tuone jinsi ya$\dfrac{1}{6}$ kubadili$\dfrac{1}{4}$ na sehemu sawa na denominator$12$ bila kutumia mifano.

Mfano$\PageIndex{3}$: conversion

$\dfrac{1}{4}$$\dfrac{1}{6}$Kubadilisha na sehemu sawa na denominator$12$, LCD yao.

Suluhisho

Kupata LCD.	LCD ya$\dfrac{1}{4}$ na$\dfrac{1}{6}$ ni 12.
Kupata idadi ya kuzidisha 4 kupata 12.	$4 \cdot \textcolor{red}{3} = 12$
Kupata idadi ya kuzidisha 6 kupata 12.	$6 \cdot \textcolor{red}{2} = 12$
Tumia sehemu sawa za Mali ili kubadilisha kila sehemu kwa sehemu sawa na LCD, kuzidisha nambari zote na denominator ya kila sehemu kwa idadi sawa.	$\begin{split} \dfrac{1}{4} \qquad & \dfrac{1}{6} \\ \dfrac{1 \cdot \textcolor{red}{3}}{4 \cdot \textcolor{red}{3}} \qquad & \dfrac{1 \cdot \textcolor{red}{2}}{6 \cdot \textcolor{red}{2}} \end{split}$
Kurahisisha nambari na denominators.	$\dfrac{3}{12} \qquad \dfrac{2}{12}$

Hatuna kupunguza sehemu ndogo. Kama tulifanya, tunataka kupata nyuma sehemu yetu ya awali na kupoteza denominator ya kawaida.

Zoezi$\PageIndex{5}$

Badilisha kwa FRACTIONS sawa na LCD:$\dfrac{3}{4}$ na$\dfrac{5}{6}$,$LCD = 12$

Jibu: $\dfrac{9}{12}, \dfrac{10}{12}$

Zoezi$\PageIndex{6}$

Badilisha kwa FRACTIONS sawa na LCD:$- \dfrac{7}{12}$ na$\dfrac{11}{15}$,$LCD = 60$

Jibu: $-\dfrac{35}{60}, \dfrac{44}{60}$

JINSI YA: KUBADILISHA SEHEMU MBILI KWA SEHEMU SAWA NA LCD YAO KAMA DENOMINATOR YA KAWAIDA

Hatua ya 1. Kupata LCD.

Hatua ya 2. Kwa kila sehemu, tambua nambari inayohitajika kuzidisha denominator ili kupata LCD.

Hatua ya 3. Tumia Mali ya sehemu sawa ili kuzidisha nambari zote na denominator kwa nambari uliyopata katika Hatua ya 2.

Hatua ya 4. Kurahisisha nambari na denominator.

Mfano$\PageIndex{4}$: conversion

$\dfrac{8}{15}$$\dfrac{11}{24}$Kubadilisha na sehemu sawa na denominator$120$, LCD yao.

Kupata idadi ambayo lazima kuzidisha 15 kupata 120.	$15 \cdot \textcolor{red}{8} = 120$
Kupata idadi ambayo lazima kuzidisha 24 kupata 120.	$24 \cdot \textcolor{red}{5} = 120$
Matumizi sawa FRACTIONS Mali.	$\dfrac{8 \cdot \textcolor{red}{8}}{15 \cdot \textcolor{red}{8}} \qquad \dfrac{11 \cdot \textcolor{red}{5}}{24 \cdot \textcolor{red}{5}}$
Kurahisisha nambari na denominators.	$\dfrac{64}{120} \qquad \dfrac{55}{120}$

Zoezi$\PageIndex{7}$

Badilisha kwa FRACTIONS sawa na LCD:$\dfrac{13}{24}$ na$\dfrac{17}{32}$, LCD$96$

Jibu: $\dfrac{52}{96}, \dfrac{51}{96}$

Zoezi$\PageIndex{8}$

Badilisha kwa FRACTIONS sawa na LCD:$\dfrac{9}{28}$ na$\dfrac{27}{32}$, LCD$224$

Jibu: $\dfrac{72}{224}, \dfrac{189}{224}$

Kuongeza na Ondoa Fractions na Denominators tofauti

Mara tu tumebadilisha sehemu mbili kwa fomu sawa na denominators ya kawaida, tunaweza kuongeza au kuziondoa kwa kuongeza au kuondoa nambari.

JINSI YA: KUONGEZA AU KUONDOA SEHEMU NDOGO NA DENOMINATORS TOFAUTI

Hatua ya 1. Kupata LCD.

Hatua ya 2. Badilisha kila sehemu kwa fomu sawa na LCD kama denominator.

Hatua ya 3. Ongeza au uondoe sehemu ndogo.

Hatua ya 4. Andika matokeo kwa fomu rahisi.

Mfano$\PageIndex{5}$: add

Ongeza:$\dfrac{1}{2} + \dfrac{1}{3}$.

Suluhisho

Kupata LCD ya 2, 3.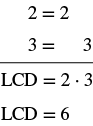
Badilisha katika sehemu ndogo sawa na LCD 6.	$\dfrac{1 \cdot \textcolor{red}{3}}{2 \cdot \textcolor{red}{3}} + \dfrac{1 \cdot \textcolor{red}{2}}{3 \cdot \textcolor{red}{2}}$
Kurahisisha nambari na denominators.	$\dfrac{3}{6} + \dfrac{2}{6}$
Ongeza.	$\dfrac{5}{6}$

Kumbuka, daima angalia ili uone kama jibu linaweza kuwa rahisi. Tangu$5$ na$6$ hawana sababu za kawaida, sehemu$\dfrac{5}{6}$ haiwezi kupunguzwa.

Zoezi$\PageIndex{9}$

Ongeza:$\dfrac{1}{4} + \dfrac{1}{3}$.

Jibu: $\dfrac{7}{12}$

Zoezi$\PageIndex{10}$

Ongeza:$\dfrac{1}{2} + \dfrac{1}{5}$.

Jibu: $\dfrac{7}{10}$

Mfano$\PageIndex{6}$: subtract

Ondoa:$\dfrac{1}{2} - \left(- \dfrac{1}{4}\right)$.

Suluhisho

Kupata LCD ya 2 na 4.
Andika upya kama sehemu sawa kwa kutumia LCD 4.	$\dfrac{1 \cdot \textcolor{red}{2}}{2 \cdot \textcolor{red}{2}} - \left(- \dfrac{1}{4}\right)$
Kurahisisha sehemu ya kwanza.	$\dfrac{2}{4} - \left(- \dfrac{1}{4}\right)$
Ondoa.	$\dfrac{2 - (-1)}{4}$
Kurahisisha.	$\dfrac{3}{4}$

Moja ya sehemu ndogo tayari ilikuwa na denominator ya kawaida, kwa hiyo tulipaswa tu kubadili sehemu nyingine.

Zoezi$\PageIndex{11}$

Ondoa:$\dfrac{1}{2} - \left(- \dfrac{1}{8}\right)$.

Jibu: $\dfrac{5}{8}$

Zoezi$\PageIndex{12}$

Ondoa:$\dfrac{1}{3} - \left(- \dfrac{1}{6}\right)$.

Jibu: $\dfrac{1}{2}$

Mfano$\PageIndex{7}$: add

Ongeza:$\dfrac{7}{12} + \dfrac{5}{18}$.

Suluhisho

Kupata LCD ya 12 na 18.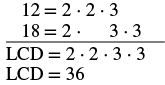
Andika upya kama sehemu ndogo sawa na LCD.	$\dfrac{7 \cdot \textcolor{red}{3}}{12 \cdot \textcolor{red}{3}} + \dfrac{5 \cdot \textcolor{red}{2}}{18 \cdot \textcolor{red}{2}}$
Kurahisisha nambari na denominators.	$\dfrac{21}{36} + \dfrac{10}{36}$
Ongeza.	$\dfrac{31}{36}$

Kwa sababu$31$ ni idadi mkuu, haina sababu sawa na$36$. Jibu ni rahisi.

Zoezi$\PageIndex{13}$

Ongeza:$\dfrac{7}{12} + \dfrac{11}{15}$.

Jibu: $\dfrac{79}{60}$

Zoezi$\PageIndex{14}$

Ongeza:$\dfrac{13}{15} + \dfrac{17}{20}$.

Jibu: $\dfrac{103}{60}$

Wakati sisi kutumia sawa Fractions Mali, kuna njia ya haraka ya kupata idadi unahitaji kuzidisha na kupata LCD. Andika mambo ya denominators na LCD kama ulivyofanya ili kupata LCD. Sababu “kukosa” za kila denominator ni namba unayohitaji.

$Mstari wa kwanza unasema 12 ni sawa na mara 2 mara 3. Kuna nafasi tupu karibu na 3. Mstari unaofuata unasema 18 sawa mara 2 mara 3. Kuna nafasi tupu kati ya 2 na ya kwanza 3. Kuna mistari nyekundu inayotokana na nafasi tupu. Hii ni kinachoitwa kama sababu kukosa. Kuna mstari usio na usawa. Chini ya mstari, inasema LCD ni sawa na mara 2 mara 3 mara 3. Chini ya hii, inasema LCD sawa 36.$

LCD,$36$, ina$2$ sababu za$2$ na$2$ sababu za$3$. Kumi na mbili ina sababu mbili za$2$, lakini moja tu ya$3$ -hivyo ni 'kukosa' moja$3$. Sisi kuzidisha nambari na denominator ya$\dfrac{7}{12}$ na$3$ kupata sehemu sawa na denominator$36$. Kumi na nane ni kukosa sababu moja ya$2$ - hivyo kuzidisha numerator$\dfrac{5}{18}$ na$2$ denominator na kupata sehemu sawa na denominator$36$. Tutatumia njia hii tunapoondoa sehemu ndogo katika mfano unaofuata.

Mfano$\PageIndex{8}$: subtract

Ondoa:$\dfrac{7}{15} − \dfrac{19}{24}$.

Suluhisho

Kupata LCD. 15 ni 'kukosa' mambo matatu ya 2 24 ni 'kukosa' sababu ya 5
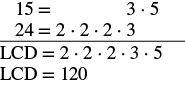Andika upya kama sehemu ndogo sawa na LCD.	$\dfrac{7 \cdot \textcolor{red}{8}}{15 \cdot \textcolor{red}{8}} - \dfrac{19 \cdot \textcolor{red}{5}}{24 \cdot \textcolor{red}{5}}$
Kurahisisha kila nambari na denominator.	$\dfrac{56}{120} - \dfrac{95}{120}$
Ondoa.	$- \dfrac{39}{120}$
Andika upya kuonyesha sababu ya kawaida ya 3.	$- \dfrac{13 \cdot 3}{40 \cdot 3}$
Ondoa jambo la kawaida ili kurahisisha.	$- \dfrac{13}{40}$

Zoezi$\PageIndex{15}$

Ondoa:$\dfrac{13}{24} − \dfrac{17}{32}$.

Jibu: $\dfrac{1}{96}$

Zoezi$\PageIndex{16}$

Ondoa:$\dfrac{21}{32} − \dfrac{9}{28}$.

Jibu: $\dfrac{75}{224}$

Mfano$\PageIndex{9}$: add

Ongeza:$- \dfrac{11}{30} + \dfrac{23}{42}$.

Suluhisho

Kupata LCD.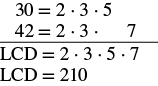
Andika upya kama sehemu ndogo sawa na LCD.	$- \dfrac{11 \cdot \textcolor{red}{7}}{30 \cdot \textcolor{red}{7}} + \dfrac{23 \cdot \textcolor{red}{5}}{42 \cdot \textcolor{red}{5}}$
Kurahisisha kila nambari na denominator.	$- \dfrac{77}{210} + \dfrac{115}{210}$
Ongeza.	$\dfrac{38}{210}$
Andika upya kuonyesha sababu ya kawaida ya 2.	$\dfrac{19 \cdot 2}{105 \cdot 2}$
Ondoa jambo la kawaida ili kurahisisha.	$\dfrac{19}{105}$

Zoezi$\PageIndex{17}$

Ongeza:$- \dfrac{13}{42} + \dfrac{17}{35}$.

Jibu: $\dfrac{37}{210}$

Zoezi$\PageIndex{18}$

Ongeza:$- \dfrac{19}{24} + \dfrac{17}{32}$.

Jibu: $-\dfrac{25}{96}$

Katika mfano unaofuata, moja ya sehemu ndogo ina variable katika nambari yake. Tunafuata hatua sawa na wakati nambari zote mbili ni namba.

Mfano$\PageIndex{10}$: add

Ongeza:$\dfrac{3}{5} + \dfrac{x}{8}$.

Suluhisho

Sehemu ndogo zina madhehebu tofauti.

Kupata LCD.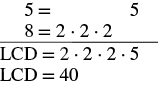
Andika upya kama sehemu ndogo sawa na LCD.	$\dfrac{3 \cdot \textcolor{red}{8}}{5 \cdot \textcolor{red}{8}} + \dfrac{x \cdot \textcolor{red}{5}}{8 \cdot \textcolor{red}{5}}$
Kurahisisha nambari na denominators.	$\dfrac{24}{40} + \dfrac{5x}{40}$
Ongeza.	$\dfrac{24 + 5x}{40}$

Hatuwezi kuongeza$24$ na kwa$5x$ kuwa si kama maneno, hivyo hatuwezi kurahisisha usemi wowote zaidi.

Zoezi$\PageIndex{19}$

Ongeza:$\dfrac{y}{6} + \dfrac{7}{9}$.

Jibu: $\dfrac{3y+14}{18}$

Zoezi$\PageIndex{20}$

Ongeza:$\dfrac{x}{6} + \dfrac{7}{15}$.

Jibu: $\dfrac{5x+14}{30}$

Wachangiaji na Majina

Template:ContribOpenStaxPreAlgebra

Ufafanuzi: Denominator ya kawaida

Mfano\(\PageIndex{1}\): lcd

Zoezi\(\PageIndex{1}\)

Zoezi\(\PageIndex{2}\)

JINSI YA: KUPATA DENOMINATOR ANGALAU YA KAWAIDA (LCD) YA SEHEMU MBILI

Mfano\(\PageIndex{2}\):

Zoezi\(\PageIndex{3}\)

Zoezi\(\PageIndex{4}\)

Ufafanuzi: Sawa Fractions Mali

Mfano\(\PageIndex{3}\): conversion

Zoezi\(\PageIndex{5}\)

Zoezi\(\PageIndex{6}\)

JINSI YA: KUBADILISHA SEHEMU MBILI KWA SEHEMU SAWA NA LCD YAO KAMA DENOMINATOR YA KAWAIDA

Mfano\(\PageIndex{4}\): conversion

Zoezi\(\PageIndex{7}\)

Zoezi\(\PageIndex{8}\)

JINSI YA: KUONGEZA AU KUONDOA SEHEMU NDOGO NA DENOMINATORS TOFAUTI

Mfano\(\PageIndex{5}\): add

Zoezi\(\PageIndex{9}\)

Zoezi\(\PageIndex{10}\)

Mfano\(\PageIndex{6}\): subtract

Zoezi\(\PageIndex{11}\)

Zoezi\(\PageIndex{12}\)

Mfano\(\PageIndex{7}\): add

Zoezi\(\PageIndex{13}\)

Zoezi\(\PageIndex{14}\)

Mfano\(\PageIndex{8}\): subtract

Zoezi\(\PageIndex{15}\)

Zoezi\(\PageIndex{16}\)

Mfano\(\PageIndex{9}\): add

Zoezi\(\PageIndex{17}\)

Zoezi\(\PageIndex{18}\)

Mfano\(\PageIndex{10}\): add

Zoezi\(\PageIndex{19}\)

Zoezi\(\PageIndex{20}\)

Kupata LCD.	LCD ya\(\dfrac{1}{4}\) na\(\dfrac{1}{6}\) ni 12.
Kupata idadi ya kuzidisha 4 kupata 12.	\(4 \cdot \textcolor{red}{3} = 12\)
Kupata idadi ya kuzidisha 6 kupata 12.	\(6 \cdot \textcolor{red}{2} = 12\)
Tumia sehemu sawa za Mali ili kubadilisha kila sehemu kwa sehemu sawa na LCD, kuzidisha nambari zote na denominator ya kila sehemu kwa idadi sawa.	\(\begin{split} \dfrac{1}{4} \qquad & \dfrac{1}{6} \\ \dfrac{1 \cdot \textcolor{red}{3}}{4 \cdot \textcolor{red}{3}} \qquad & \dfrac{1 \cdot \textcolor{red}{2}}{6 \cdot \textcolor{red}{2}} \end{split}\)
Kurahisisha nambari na denominators.	\(\dfrac{3}{12} \qquad \dfrac{2}{12}\)

Kupata idadi ambayo lazima kuzidisha 15 kupata 120.	\(15 \cdot \textcolor{red}{8} = 120\)
Kupata idadi ambayo lazima kuzidisha 24 kupata 120.	\(24 \cdot \textcolor{red}{5} = 120\)
Matumizi sawa FRACTIONS Mali.	\(\dfrac{8 \cdot \textcolor{red}{8}}{15 \cdot \textcolor{red}{8}} \qquad \dfrac{11 \cdot \textcolor{red}{5}}{24 \cdot \textcolor{red}{5}}\)
Kurahisisha nambari na denominators.	\(\dfrac{64}{120} \qquad \dfrac{55}{120}\)

Kupata LCD ya 2, 3.
Badilisha katika sehemu ndogo sawa na LCD 6.	\(\dfrac{1 \cdot \textcolor{red}{3}}{2 \cdot \textcolor{red}{3}} + \dfrac{1 \cdot \textcolor{red}{2}}{3 \cdot \textcolor{red}{2}}\)
Kurahisisha nambari na denominators.	\(\dfrac{3}{6} + \dfrac{2}{6}\)
Ongeza.	\(\dfrac{5}{6}\)

Kupata LCD ya 2 na 4.
Andika upya kama sehemu sawa kwa kutumia LCD 4.	\(\dfrac{1 \cdot \textcolor{red}{2}}{2 \cdot \textcolor{red}{2}} - \left(- \dfrac{1}{4}\right)\)
Kurahisisha sehemu ya kwanza.	\(\dfrac{2}{4} - \left(- \dfrac{1}{4}\right)\)
Ondoa.	\(\dfrac{2 - (-1)}{4}\)
Kurahisisha.	\(\dfrac{3}{4}\)

Kupata LCD ya 12 na 18.
Andika upya kama sehemu ndogo sawa na LCD.	\(\dfrac{7 \cdot \textcolor{red}{3}}{12 \cdot \textcolor{red}{3}} + \dfrac{5 \cdot \textcolor{red}{2}}{18 \cdot \textcolor{red}{2}}\)
Kurahisisha nambari na denominators.	\(\dfrac{21}{36} + \dfrac{10}{36}\)
Ongeza.	\(\dfrac{31}{36}\)

Kupata LCD. 15 ni 'kukosa' mambo matatu ya 2 24 ni 'kukosa' sababu ya 5
Andika upya kama sehemu ndogo sawa na LCD.	\(\dfrac{7 \cdot \textcolor{red}{8}}{15 \cdot \textcolor{red}{8}} - \dfrac{19 \cdot \textcolor{red}{5}}{24 \cdot \textcolor{red}{5}}\)
Kurahisisha kila nambari na denominator.	\(\dfrac{56}{120} - \dfrac{95}{120}\)
Ondoa.	\(- \dfrac{39}{120}\)
Andika upya kuonyesha sababu ya kawaida ya 3.	\(- \dfrac{13 \cdot 3}{40 \cdot 3}\)
Ondoa jambo la kawaida ili kurahisisha.	\(- \dfrac{13}{40}\)

Kupata LCD.
Andika upya kama sehemu ndogo sawa na LCD.	\(- \dfrac{11 \cdot \textcolor{red}{7}}{30 \cdot \textcolor{red}{7}} + \dfrac{23 \cdot \textcolor{red}{5}}{42 \cdot \textcolor{red}{5}}\)
Kurahisisha kila nambari na denominator.	\(- \dfrac{77}{210} + \dfrac{115}{210}\)
Ongeza.	\(\dfrac{38}{210}\)
Andika upya kuonyesha sababu ya kawaida ya 2.	\(\dfrac{19 \cdot 2}{105 \cdot 2}\)
Ondoa jambo la kawaida ili kurahisisha.	\(\dfrac{19}{105}\)

Kupata LCD.
Andika upya kama sehemu ndogo sawa na LCD.	\(\dfrac{3 \cdot \textcolor{red}{8}}{5 \cdot \textcolor{red}{8}} + \dfrac{x \cdot \textcolor{red}{5}}{8 \cdot \textcolor{red}{5}}\)
Kurahisisha nambari na denominators.	\(\dfrac{24}{40} + \dfrac{5x}{40}\)
Ongeza.	\(\dfrac{24 + 5x}{40}\)