Skip to main content
Global

4.7: Ongeza na Ondoa Fractions na Denominators ya kawaida

  1. Last updated
  2. Save as PDF
  • Page ID
    173401

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Mfano wa sehemu ya kuongeza
    • Ongeza sehemu ndogo na denominator ya kawaida
    • Uondoaji wa sehemu ya mfano
    • Ondoa sehemu ndogo na denominator ya kawaida
    kuwa tayari!

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kurahisisha:\(2x + 9 + 3x − 4\). Ikiwa umekosa tatizo hili, kagua Mfano 2.2.10.
    2. Chora mfano wa sehemu\(\dfrac{3}{4}\). Ikiwa umekosa tatizo hili, tathmini Mfano 4.1.2.
    3. Kurahisisha:\(\dfrac{3 + 2}{6}\). Kama amekosa tatizo hili, mapitio Mfano 4.3.12.

    Model Fraction Aidha

    Ni robo ngapi zinaonyeshwa? Robo moja pamoja na\(2\) robo sawa na\(3\) robo.

    Robo tatu za Marekani zinaonyeshwa. Moja inavyoonyeshwa upande wa kushoto, na mbili zinaonyeshwa upande wa kulia.

    Kielelezo\(\PageIndex{1}\)

    Kumbuka, robo ni kweli FRACTIONS ya dola. Quarters ni njia nyingine ya kusema nne. Hivyo picha ya sarafu inaonyesha kwamba

    \[\begin{split} \dfrac{1}{4} \qquad \qquad \qquad \dfrac{2}{4} \qquad & \qquad \qquad \dfrac{3}{4} \\ one \; quarter + two \; quarters &= three\; quarters \end{split} \nonumber \]

    Hebu tumia miduara ya sehemu ili mfano mfano huo,\(\dfrac{1}{4} + \dfrac{2}{4}\).

    Anza na\(\dfrac{1}{4}\) kipande kimoja. \(\dfrac{1}{4}\)
    Ongeza\(\dfrac{1}{4}\) vipande viwili zaidi. 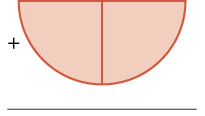\(+ \dfrac{2}{4}\)
    Matokeo yake ni\(\dfrac{3}{4}\). 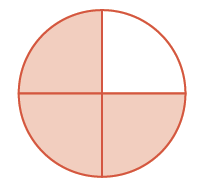\(\dfrac{3}{4}\)

    Hivyo tena, tunaona kwamba

    \[\dfrac{1}{4} + \dfrac{2}{4} = \dfrac{3}{4} \nonumber \]

    Mfano\(\PageIndex{1}\): addition

    Tumia mfano ili kupata jumla\(\dfrac{3}{8} + \dfrac{2}{8}\).

    Suluhisho

    Anza na\(\dfrac{1}{8}\) vipande vitatu. 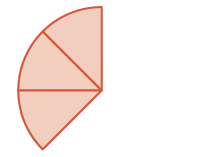\(\dfrac{3}{8}\)
    Ongeza\(\dfrac{1}{8}\) vipande viwili. 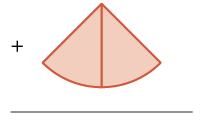\(+ \dfrac{2}{8}\)
    Kuna\(\dfrac{1}{8}\) vipande ngapi? 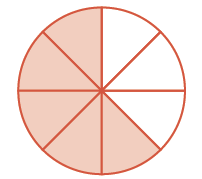\(\dfrac{5}{8}\)

    Kuna\(\dfrac{1}{8}\) vipande tano, au tano na nane. Mfano unaonyesha kwamba\(\dfrac{3}{8} + \dfrac{2}{8} = \dfrac{5}{8}\).

    Zoezi\(\PageIndex{1}\)

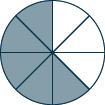
    Tumia mfano ili kupata kila jumla. Onyesha mchoro ili kuonyesha mfano wako. \[\dfrac{1}{8} + \dfrac{4}{8} \nonumber \]

    Jibu

    \(\dfrac{5}{8}\)

    CNX_BMath_Figure_04_04_004_img.jpg

    Zoezi\(\PageIndex{2}\)

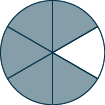
    Tumia mfano ili kupata kila jumla. Onyesha mchoro ili kuonyesha mfano wako. \[\dfrac{1}{6} + \dfrac{4}{6} \nonumber \]

    Jibu

    \(\dfrac{5}{6}\)

    CNX_BMath_Figure_04_04_005_img.jpg

    Ongeza sehemu ndogo na Denominator ya kawaida

    Mfano\(\PageIndex{1}\) unaonyesha kwamba kuongeza vipande sawa-size maana kwamba sehemu ndogo na denominator sawa-sisi tu kuongeza idadi ya vipande.

    Ufafanuzi: Sehemu ya kuongeza

    Ikiwa\(a\),\(b\), na\(c\) ni namba ambapo\(c ≠ 0\), basi

    \[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\]

    Ili kuongeza sehemu ndogo na denominator ya kawaida, ongeza nambari na uweke jumla juu ya denominator ya kawaida.

    Mfano\(\PageIndex{2}\): addition

    Pata jumla:\(\dfrac{3}{5} + \dfrac{1}{5}\).

    Suluhisho

    Ongeza nambari na uweke jumla juu ya denominator ya kawaida. \(\dfrac{3 + 1}{5}\)
    Kurahisisha. \(\dfrac{4}{5}\)
    Zoezi\(\PageIndex{3}\)

    Kupata kila jumla:\(\dfrac{3}{6} + \dfrac{2}{6}\).

    Jibu

    \(\dfrac{5}{6}\)

    Zoezi\(\PageIndex{4}\)

    Kupata kila jumla:\(\dfrac{3}{10} + \dfrac{7}{10}\).

    Jibu

    \(1\)

    Mfano\(\PageIndex{3}\): addition

    Pata jumla:\(\dfrac{x}{3} + \dfrac{2}{3}\).

    Suluhisho

    Ongeza nambari na uweke jumla juu ya denominator ya kawaida. \(\dfrac{x + 2}{3}\)

    Kumbuka kwamba hatuwezi kurahisisha sehemu hii tena. Kwa kuwa\(x\) na\(2\) si kama maneno, hatuwezi kuchanganya nao.

    Zoezi\(\PageIndex{5}\)

    Pata jumla:\(\dfrac{x}{4} + \dfrac{3}{4}\).

    Jibu

    \(\dfrac{x+3}{4}\)

    Zoezi\(\PageIndex{6}\)

    Pata jumla:\(\dfrac{y}{8} + \dfrac{5}{8}\).

    Jibu

    \(\dfrac{y+5}{8}\)

    Mfano\(\PageIndex{4}\): addition

    Pata jumla:\(− \dfrac{9}{d} + \dfrac{3}{d}\).

    Suluhisho

    Tutaanza kwa kuandika tena sehemu ya kwanza na ishara hasi katika nambari.

    \[− \dfrac{a}{b} = \dfrac{−a}{b} \nonumber \]

    Andika upya sehemu ya kwanza na hasi katika nambari. \(\dfrac{-9}{d} + \dfrac{3}{d}\)
    Ongeza nambari na uweke jumla juu ya denominator ya kawaida. \(\dfrac{-9 + 3}{d}\)
    Kurahisisha nambari. \(\dfrac{-6}{d}\)
    Andika upya na ishara hasi mbele ya sehemu. \(- \dfrac{6}{d}\)
    Zoezi\(\PageIndex{7}\)

    Pata jumla:\(− \dfrac{7}{d} + \dfrac{8}{d}\).

    Jibu

    \(\dfrac{1}{d}\)

    Zoezi\(\PageIndex{8}\)

    Pata jumla:\(− \dfrac{6}{m} + \dfrac{9}{m}\).

    Jibu

    \(\dfrac{3}{m}\)

    Mfano\(\PageIndex{5}\): addition

    Pata jumla:\(\dfrac{2n}{11} + \dfrac{5n}{11}\).

    Suluhisho

    Ongeza nambari na uweke jumla juu ya denominator ya kawaida. \(\dfrac{2n + 5n}{11}\)
    Kuchanganya kama maneno. \(\dfrac{7n}{11}\)
    Zoezi\(\PageIndex{9}\)

    Pata jumla:\(\dfrac{3p}{8} + \dfrac{6p}{8}\).

    Jibu

    \(\dfrac{9p}{8}\)

    Zoezi\(\PageIndex{10}\)

    Pata jumla:\(\dfrac{2q}{5} + \dfrac{7q}{5}\).

    Jibu

    \(\dfrac{9q}{5}\)

    Mfano\(\PageIndex{6}\): addition

    Pata jumla:\(− \dfrac{3}{12} + \left(− \dfrac{5}{12}\right)\).

    Suluhisho

    Ongeza nambari na uweke jumla juu ya denominator ya kawaida. \(\dfrac{-3 + (-5)}{12}\)
    Ongeza. \(\dfrac{-8}{12}\)
    Kurahisisha sehemu. \(-\dfrac{2}{3}\)
    Zoezi\(\PageIndex{11}\)

    Kupata kila jumla:\(− \dfrac{4}{15} + \left(− \dfrac{6}{15}\right)\).

    Jibu

    \(-\dfrac{2}{3}\)

    Zoezi\(\PageIndex{12}\)

    Kupata kila jumla:\(− \dfrac{5}{21} + \left(− \dfrac{9}{21}\right)\).

    Jibu

    \(-\dfrac{2}{3}\)

    Model sehemu Ondoa

    Kuondoa sehemu mbili na denominators ya kawaida ni kama kuongeza sehemu ndogo. Fikiria pizza iliyokatwa katika\(12\) vipande. Tuseme vipande tano huliwa kwa chakula cha jioni. Hii ina maana kwamba, baada ya chakula cha jioni, kuna vipande saba (au\(\dfrac{7}{12}\) vya pizza) vilivyoachwa katika sanduku. Ikiwa Leonardo anakula\(2\) vipande hivi vilivyobaki (au\(\dfrac{2}{12}\) pizza), ni kiasi gani kinachoachwa? Kutakuwa na\(5\) vipande vilivyoachwa (au\(\dfrac{5}{12}\) vya pizza).

    \[\dfrac{7}{12} - \dfrac{2}{12} = \dfrac{5}{12} \nonumber \]

    Hebu tumia miduara ya sehemu ili mfano mfano huo,\(\dfrac{7}{12} − \dfrac{2}{12}\). Anza na\(\dfrac{1}{12}\) vipande saba. Chukua\(\dfrac{1}{12}\) vipande viwili. Ni ngapi kumi na mbili wanaachwa?

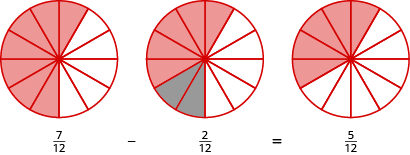
    Chini inasoma 7 kumi na mbili chini ya 2 kumi na mbili sawa na kumi na mbili. Zaidi ya kumi na mbili, kuna mduara umegawanywa katika vipande 12 sawa, na vipande 7 vimevuliwa machungwa. Zaidi ya 2 kumi na mbili, mduara huo unaonyeshwa, lakini 2 kati ya vipande 7 vimevuliwa kwa kijivu. Zaidi ya 5 kumi na mbili, vipande 2 vya kijivu havivuli tena, kwa hiyo kuna mduara umegawanyika katika vipande 12 na 5 vya vipande vilivyovuliwa machungwa.

    Kielelezo\(\PageIndex{2}\)

    Tena, tuna kumi na mbili tano,\(\dfrac{5}{12}\).

    Mfano\(\PageIndex{7}\): difference

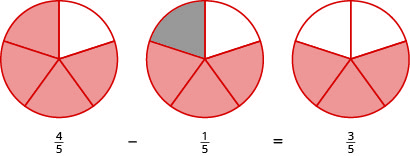
    Tumia miduara ya sehemu ili kupata tofauti:\(\dfrac{4}{5} − \dfrac{1}{5}\).

    Suluhisho

    Anza na\(\dfrac{1}{5}\) vipande vinne. Chukua\(\dfrac{1}{5}\) kipande kimoja. Hesabu ngapi tano zimeachwa. Kuna\(\dfrac{1}{5}\) vipande vitatu vilivyoachwa.

    Chini inasoma 4 tano chini ya 1 tano sawa na 3 tano. Zaidi ya 4 ya tano, kuna mduara umegawanywa katika vipande 5 sawa, na vipande 4 vimevuliwa katika machungwa. Zaidi ya 1 ya tano, mduara huo unaonyeshwa, lakini 1 kati ya vipande 4 vilivyovuliwa ni kivuli katika kijivu. Zaidi ya 3 ya tano, kipande cha kijivu cha 1 hakina kivuli tena, kwa hiyo kuna mduara umegawanyika katika vipande 5 na vipande 3 vilivyovuliwa machungwa.

    Zoezi\(\PageIndex{13}\)

    Tumia mfano ili kupata kila tofauti. Onyesha mchoro ili kuonyesha mfano wako. \(\dfrac{7}{8} − \dfrac{4}{8}\)

    Jibu

    \(\dfrac{3}{8}\), mifano inaweza kutofautiana.

    Zoezi\(\PageIndex{14}\)

    Tumia mfano ili kupata kila tofauti. Onyesha mchoro ili kuonyesha mfano wako. \(\dfrac{5}{6} − \dfrac{4}{6}\)

    Jibu

    \(\dfrac{1}{6}\), mifano inaweza kutofautiana.

    Ondoa FRACTIONS na Denominator ya kawaida

    Tunaondoa sehemu ndogo na denominator ya kawaida kwa njia sawa na sisi kuongeza sehemu ndogo na denominator ya kawaida.

    Ufafanuzi: Kuondoa sehemu

    Ikiwa\(a\),\(b\), na\(c\) ni namba ambapo\(c ≠ 0\), basi

    \[\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}\]

    Ili kuondoa sehemu ndogo na denominator ya kawaida, tunaondoa nambari na kuweka tofauti juu ya denominator ya kawaida.

    Mfano\(\PageIndex{8}\): difference

    Kupata tofauti:\(\dfrac{23}{24} − \dfrac{14}{24}\).

    Suluhisho

    Ondoa nambari na uweke tofauti juu ya denominator ya kawaida. \(\dfrac{23 - 14}{24}\)
    Kurahisisha nambari. \(\dfrac{9}{24}\)
    Kurahisisha sehemu kwa kuondoa mambo ya kawaida. \(\dfrac{3}{8}\)
    Zoezi\(\PageIndex{15}\)

    Kupata tofauti:\(\dfrac{19}{28} − \dfrac{7}{28}\).

    Jibu

    \(\dfrac{3}{7}\)

    Zoezi\(\PageIndex{16}\)

    Kupata tofauti:\(\dfrac{27}{32} − \dfrac{11}{32}\).

    Jibu

    \(\dfrac{1}{2}\)

    Mfano\(\PageIndex{9}\): difference

    Kupata tofauti:\(\dfrac{y}{6} − \dfrac{1}{6}\).

    Suluhisho

    Ondoa nambari na uweke tofauti juu ya denominator ya kawaida. \(\dfrac{y - 1}{6}\)

    Sehemu ni rahisi kwa sababu hatuwezi kuchanganya maneno katika nambari.

    Zoezi\(\PageIndex{17}\)

    Kupata tofauti:\(\dfrac{x}{7} − \dfrac{2}{7}\).

    Jibu

    \(\dfrac{x-2}{7}\)

    Zoezi\(\PageIndex{18}\)

    Kupata tofauti:\(\dfrac{y}{14} − \dfrac{13}{14}\).

    Jibu

    \(\dfrac{y-13}{14}\)

    Mfano\(\PageIndex{10}\): difference

    Kupata tofauti:\(− \dfrac{10}{x} − \dfrac{4}{x}\).

    Suluhisho

    Kumbuka, sehemu\(− \dfrac{10}{x}\) inaweza kuandikwa kama\(\dfrac{−10}{x}\).

    Ondoa nambari. \(\dfrac{-10 - 4}{x}\)
    Kurahisisha. \(\dfrac{-14}{x}\)
    Andika upya na ishara hasi mbele ya sehemu. \(- \dfrac{14}{x}\)
    Zoezi\(\PageIndex{19}\)

    Kupata tofauti:\(− \dfrac{9}{x} − \dfrac{7}{x}\).

    Jibu

    \(-\dfrac{16}{x}\)

    Zoezi\(\PageIndex{20}\)

    Kupata tofauti:\(− \dfrac{17}{a} − \dfrac{5}{a}\).

    Jibu

    \(-\dfrac{22}{a}\)

    Sasa hebu tufanye mfano unaohusisha wote kuongeza na kuondoa.

    Mfano\(\PageIndex{11}\): simplify

    Kurahisisha:\(\dfrac{3}{8} + \left(- \dfrac{5}{8}\right) − \dfrac{1}{8}\).

    Suluhisho

    Kuchanganya nambari juu ya denominator ya kawaida. \(\dfrac{3 + (-5) - 1}{8}\)
    Kurahisisha namba, kufanya kazi kushoto kwenda kulia. \(\dfrac{-2 - 1}{8}\)
    Ondoa maneno katika namba. \(\dfrac{-3}{8}\)
    Andika upya na ishara hasi mbele ya sehemu. \(- \dfrac{3}{8}\)
    Zoezi\(\PageIndex{21}\)

    Kurahisisha:\(\dfrac{2}{5} + \left(− \dfrac{4}{5}\right) − \dfrac{3}{5}\).

    Jibu

    \(-1\)

    Zoezi\(\PageIndex{22}\)

    Kurahisisha:\(\dfrac{5}{9} + \left(− \dfrac{4}{9}\right) − \dfrac{7}{9}\).

    Jibu

    \(-\dfrac{2}{3}\)

    Dhana muhimu

    • Sehemu ya kuongeza
      • Kama\(a,b,\),na\(c\) ni idadi ambapo\(c\neq 0\), basi\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\)
      • Ili kuongeza sehemu ndogo, ongeza nambari na uweke jumla juu ya denominator ya kawaida.
    • Kuondoa sehemu
      • Kama\(a,b,\),na\(c\) ni idadi ambapo\(c\neq 0\), basi\(\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}\)
      • Ili kuondoa sehemu ndogo, toa nambari na uweke tofauti juu ya denominator ya kawaida.

    Mazoezi hufanya kamili

    Model sehemu Aidha

    Katika mazoezi yafuatayo, tumia mfano ili kuongeza sehemu ndogo. Onyesha mchoro ili kuonyesha mfano wako.

    1. \(\dfrac{2}{5} + \dfrac{1}{5}\)
    2. \(\dfrac{3}{10} + \dfrac{4}{10}\)
    3. \(\dfrac{1}{6} + \dfrac{3}{6}\)
    4. \(\dfrac{3}{8} + \dfrac{3}{8}\)

    Ongeza sehemu ndogo na Denominator ya kawaida

    Katika mazoezi yafuatayo, tafuta kila jumla.

    1. \(\dfrac{4}{9} + \dfrac{1}{9}\)
    2. \(\dfrac{2}{9} + \dfrac{5}{9}\)
    3. \(\dfrac{6}{13} + \dfrac{7}{13}\)
    4. \(\dfrac{9}{15} + \dfrac{7}{15}\)
    5. \(\dfrac{x}{4} + \dfrac{3}{4}\)
    6. \(\dfrac{y}{3} + \dfrac{2}{3}\)
    7. \(\dfrac{7}{p} + \dfrac{9}{p}\)
    8. \(\dfrac{8}{q} + \dfrac{6}{q}\)
    9. \(\dfrac{8b}{9} + \dfrac{3b}{9}\)
    10. \(\dfrac{5a}{7} + \dfrac{4a}{7}\)
    11. \(\dfrac{-12y}{8} + \dfrac{3y}{8}\)
    12. \(\dfrac{-11x}{5} + \dfrac{7x}{5}\)
    13. \(− \dfrac{1}{8} + \left(− \dfrac{3}{8}\right)\)
    14. \(− \dfrac{1}{8} + \left(− \dfrac{5}{8}\right)\)
    15. \(− \dfrac{3}{16} + \left(− \dfrac{7}{16}\right)\)
    16. \(− \dfrac{5}{16} + \left(− \dfrac{9}{16}\right)\)
    17. \(− \dfrac{8}{17} + \dfrac{15}{17}\)
    18. \(− \dfrac{9}{19} + \dfrac{17}{19}\)
    19. \(− \dfrac{6}{13} + \left(− \dfrac{10}{13}\right) + \left(- \dfrac{12}{13}\right)\)
    20. \(− \dfrac{5}{12} + \left(− \dfrac{7}{12}\right) + \left(- \dfrac{11}{12}\right)\)

    Model sehemu Ondoa

    Katika mazoezi yafuatayo, tumia mfano wa kuondoa sehemu ndogo. Onyesha mchoro ili kuonyesha mfano wako.

    1. \(\dfrac{5}{8} − \dfrac{2}{8}\)
    2. \(\dfrac{5}{6} − \dfrac{2}{6}\)

    Ondoa FRACTIONS na Denominator ya kawaida

    Katika mazoezi yafuatayo, tafuta tofauti.

    1. \(\dfrac{4}{5} − \dfrac{1}{5}\)
    2. \(\dfrac{4}{5} − \dfrac{3}{5}\)
    3. \(\dfrac{11}{15} − \dfrac{7}{15}\)
    4. \(\dfrac{9}{13} − \dfrac{4}{13}\)
    5. \(\dfrac{11}{12} − \dfrac{5}{12}\)
    6. \(\dfrac{7}{12} − \dfrac{5}{12}\)
    7. \(\dfrac{4}{21} − \dfrac{19}{21}\)
    8. \(- \dfrac{8}{9} − \dfrac{16}{9}\)
    9. \(\dfrac{y}{17} − \dfrac{9}{17}\)
    10. \(\dfrac{x}{19} − \dfrac{8}{19}\)
    11. \(\dfrac{5y}{8} − \dfrac{7}{8}\)
    12. \(\dfrac{11z}{13} − \dfrac{8}{13}\)
    13. \(- \dfrac{8}{d} − \dfrac{3}{d}\)
    14. \(- \dfrac{7}{c} − \dfrac{7}{c}\)
    15. \(- \dfrac{23}{u} − \dfrac{15}{u}\)
    16. \(- \dfrac{29}{v} − \dfrac{26}{v}\)
    17. \(- \dfrac{6c}{7} − \dfrac{5c}{7}\)
    18. \(- \dfrac{12d}{11} − \dfrac{9d}{11}\)
    19. \(\dfrac{-4r}{13} − \dfrac{5r}{13}\)
    20. \(\dfrac{-7s}{3} − \dfrac{7s}{3}\)
    21. \(- \dfrac{3}{5} − \left(- \dfrac{4}{5}\right)\)
    22. \(- \dfrac{3}{7} − \left(- \dfrac{5}{7}\right)\)
    23. \(- \dfrac{7}{9} − \left(- \dfrac{5}{9}\right)\)
    24. \(- \dfrac{8}{11} − \left(- \dfrac{5}{11}\right)\)

    Mazoezi ya mchanganyiko

    Katika mazoezi yafuatayo, fanya operesheni iliyoonyeshwa na uandike majibu yako kwa fomu rahisi.

    1. \(− \dfrac{5}{18} \cdot \dfrac{9}{10}\)
    2. \(− \dfrac{3}{14} \cdot \dfrac{7}{12}\)
    3. \(\dfrac{n}{5} − \dfrac{4}{5}\)
    4. \(\dfrac{6}{11} − \dfrac{s}{11}\)
    5. \(- \dfrac{7}{24} − \dfrac{2}{24}\)
    6. \(- \dfrac{5}{18} − \dfrac{1}{18}\)
    7. \(\dfrac{8}{15} \div \dfrac{12}{5}\)
    8. \(\dfrac{7}{12} \div \dfrac{9}{28}\)

    kila siku Math

    1. Trail Mix Jacob ni kuchanganya pamoja karanga na zabibu kufanya uchaguzi mchanganyiko. Ana chupa\(\dfrac{6}{10}\) ya karanga na\(\dfrac{3}{10}\) ya chupa ya zabibu. Kiasi gani cha uchaguzi anaweza kufanya?
    2. Baking Janet mahitaji\(\dfrac{5}{8}\) ya kikombe cha unga kwa mapishi yeye ni kufanya. Ana kikombe\(\dfrac{3}{8}\) cha unga tu na ataomba kukopa wengine kutoka kwa jirani yake ya karibu. Ni kiasi gani cha unga anapaswa kukopa?

    Mazoezi ya kuandika

    1. Greg imeshuka kesi yake ya bits drill na tatu ya bits akaanguka nje. Kesi hiyo ina mipaka ya bits za kuchimba, na mipaka hupangwa ili kutoka ndogo hadi kubwa. Greg mahitaji ya kuweka bits kwamba akaanguka nyuma katika kesi katika inafaa tupu. Je, bits tatu huenda wapi? Eleza jinsi unavyojua.

    Bits katika kesi:\(\dfrac{1}{16}, \dfrac{1}{8}\), ___, ___\(\dfrac{5}{16}, \dfrac{3}{8}\), ___,\(\dfrac{1}{2}, \dfrac{9}{16}, \dfrac{5}{8}\).

    Bits kwamba akaanguka nje:\(\dfrac{7}{16}, \dfrac{3}{16}, \dfrac{1}{4}\).

    1. Baada ya chama, Lupe ina\(\dfrac{5}{12}\) ya jibini pizza,\(\dfrac{4}{12}\) ya pepperoni pizza, na\(\dfrac{4}{12}\) ya veggie pizza kushoto. Je! Vipande vyote vinafaa katika sanduku la pizza 1? Eleza hoja zako.

    Self Check

    (a) Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

    (b) Kwa kiwango cha 1—10, ungewezaje kupima ujuzi wako wa sehemu hii kwa kuzingatia majibu yako kwenye orodha? Unawezaje kuboresha hii?

    Wachangiaji na Majina