Skip to main content
Global

3.1: Utangulizi wa Integers (Sehemu ya 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    173364

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Pata nambari nzuri na hasi kwenye mstari wa nambari
    • Amri idadi nzuri na hasi
    • Kupata kupinga
    • Kurahisisha maneno na thamani kamili
    • Tafsiri misemo ya neno kwa maneno na integers
    kuwa tayari!

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Plot\(0\)\(1\),, na\(3\) kwenye mstari wa nambari. Ikiwa umekosa tatizo hili, kagua Mfano 1.1.1.
    2. Jaza ishara sahihi: (\(=\),\(<\), au\(>\)):\(2\) ___\(4\) Ikiwa umekosa tatizo hili, kagua Mfano 2.1.2.

    Pata Hesabu nzuri na Hasi kwenye Nambari ya Nambari

    Je! Unaishi mahali ambapo ina baridi kali sana? Je! Umewahi kupata joto chini ya sifuri? Ikiwa ndivyo, tayari umejifunza namba hasi. Nambari hasi ni namba ambayo ni chini ya\(0\). Joto la baridi sana hupimwa kwa digrii chini ya sifuri na inaweza kuelezewa na namba hasi. Kwa mfano,\(-1^{\circ}\) F (kusoma kama “hasi shahada moja Fahrenheit”) ni\(1\) shahada chini\(0\). Ishara ndogo inavyoonyeshwa kabla ya nambari ili kuonyesha kuwa ni hasi. Kielelezo\(\PageIndex{1}\)\(-20^{\circ}\) kinaonyesha F, ambayo ni\(20\) digrii chini\(0\).

    Takwimu hii ni thermometer iliyoongezwa kwa digrii Fahrenheit. Thermometer ina kusoma kwa digrii 20.

    Kielelezo\(\PageIndex{1}\): Joto chini ya sifuri ni ilivyoelezwa na idadi hasi.

    Joto sio tu namba hasi. Overdraft ya benki ni mfano mwingine wa idadi hasi. Ikiwa mtu anaandika hundi kwa zaidi kuliko alivyo katika akaunti yake, usawa wake utakuwa hasi.

    Uinuko unaweza pia kuwakilishwa na idadi hasi. Mwinuko kwenye usawa wa bahari ni\(0\) miguu. Uinuko juu ya usawa wa bahari ni chanya na miinuko chini ya usawa wa bahari ni hasi. Mwinuko wa Bahari ya Chumvi, unaopakana na Israeli na Yordani, ni karibu\(1,302\) miguu chini ya usawa wa bahari, hivyo mwinuko wa Bahari ya Chumvi unaweza kuwakilishwa kama\(−1,302\) miguu. Angalia Kielelezo\(\PageIndex{2}\).

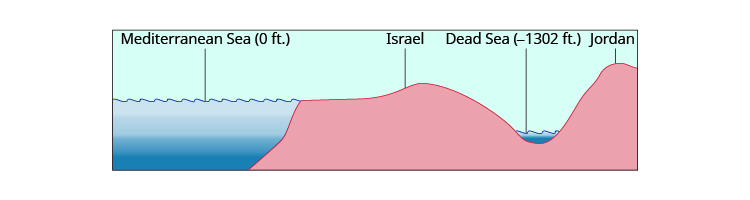
    Takwimu hii ni kuchora kwa mtazamo wa upande wa pwani ya Israeli, kuonyesha mwinuko tofauti. Bahari ya Mediterranean inaitwa 0 miguu mwinuko na Bahari ya Chumvi ni kinachoitwa hasi 1302 miguu mwinuko. Nchi ya Yordani pia imeandikwa katika takwimu.

    Kielelezo\(\PageIndex{2}\): Upeo wa Bahari ya Mediterane una mwinuko wa ft 0. Mchoro unaonyesha kwamba milima ya jirani ina miinuko ya juu (chanya) ilhali Bahari ya Chumvi ina mwinuko wa chini (hasi).

    Kina chini ya uso wa bahari pia kinaelezewa na idadi hasi. Manowari, kwa mfano, inaweza kushuka kwa kina cha\(500\) miguu. Msimamo wake ingekuwa\(−500\) miguu kama kinachoitwa katika Kielelezo\(\PageIndex{3}\).

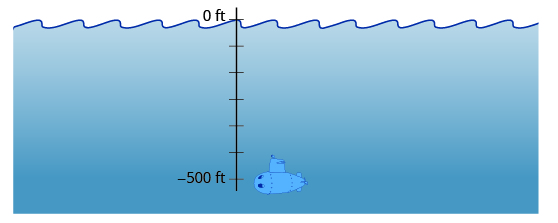
    Takwimu hii ni kuchora kwa manowari chini ya maji. Katika maji pia ni mstari wa nambari ya wima, uliowekwa kwa miguu. Mstari wa namba una futi 0 usoni na hasi futi 500 chini ya maji ambako manowari iko.

    Kielelezo\(\PageIndex{3}\): Kina chini ya usawa wa bahari ni ilivyoelezwa na idadi hasi. Manowari 500 ft chini ya usawa wa bahari ni futi -500.

    Nambari zote nzuri na hasi zinaweza kuwakilishwa kwenye mstari wa nambari. Kumbuka kwamba idadi line kuundwa katika Kuongeza Hesabu nzima ilianza saa\(0\) na ilionyesha idadi kuhesabu kuongezeka kwa haki kama inavyoonekana katika Kielelezo\(\PageIndex{4}\). Nambari za kuhesabu (\(1, 2, 3, …\)) kwenye mstari wa nambari zote ni chanya. Tunaweza kuandika ishara ya pamoja\(+\), kabla ya idadi nzuri kama vile\(+2\) au\(+3\), lakini ni desturi ya kuacha ishara ya pamoja na kuandika namba tu. Ikiwa hakuna ishara, nambari hiyo inadhaniwa kuwa chanya.

    Takwimu hii ni mstari wa nambari uliowekwa kutoka 0 hadi 6.

    Kielelezo\(\PageIndex{4}\)

    Sasa tunahitaji kupanua mstari wa nambari ili kuingiza namba hasi. Tunaweka vitengo kadhaa upande wa kushoto wa sifuri, kuweka vipindi upana sawa na wale walio upande mzuri. Tunaweka alama na namba hasi, kuanzia na alama ya\(-1\) kwanza upande wa kushoto wa\(0, -2\) alama inayofuata, na kadhalika. Angalia Kielelezo\(\PageIndex{5}\).

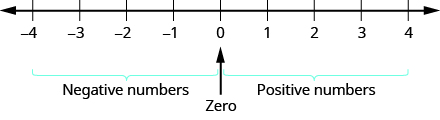
    Takwimu hii ni mstari wa namba na 0 katikati. Kisha, kuongeza ina idadi nzuri 1 hadi 4 kwa haki ya 0 na namba hasi, hasi 1 hadi hasi 4 upande wa kushoto wa 0.

    Kielelezo\(\PageIndex{5}\): Katika mstari wa nambari, namba nzuri ni haki ya sifuri. Nambari mbaya ni upande wa kushoto wa sifuri. Nini kuhusu sifuri? Zero sio chanya wala hasi.

    Mishale kwenye mwisho wowote wa mstari inaonyesha kwamba mstari wa nambari unaendelea milele katika kila mwelekeo. Hakuna idadi kubwa zaidi na hakuna nambari ndogo zaidi.

    Mfano\(\PageIndex{1}\): plot on the number line

    Plot namba kwenye mstari wa nambari:

    1. \(3\)
    2. \(-3\)
    3. \(-2\)

    Suluhisho

    Chora mstari wa nambari. Mark\(0\) katika kituo na studio vitengo kadhaa kwa upande wa kushoto na kulia.

    1. Ili kupanga njama\(3\), kuanza\(0\) na kuhesabu vitengo vitatu kwa haki. Weka hatua kama inavyoonekana kwenye Kielelezo\(\PageIndex{6}\).

    Takwimu hii ni mstari wa nambari uliowekwa kutoka hasi 4 hadi 4, na hatua ya 3 iliyoandikwa na dot.

    Kielelezo\(\PageIndex{6}\)

    1. Ili kupanga njama\(-3\), kuanza\(0\) na kuhesabu vitengo vitatu upande wa kushoto. Weka hatua kama inavyoonekana kwenye Kielelezo\(\PageIndex{7}\).

    Takwimu hii ni mstari wa nambari uliowekwa kutoka hasi 4 hadi 4, na hatua hasi 3 iliyoandikwa na dot.

    Kielelezo\(\PageIndex{7}\)

    1. Ili kupanga njama\(-2\), kuanza\(0\) na kuhesabu vitengo viwili upande wa kushoto. Weka hatua kama inavyoonekana kwenye Kielelezo\(\PageIndex{8}\).

    Takwimu hii ni mstari wa nambari ulioongezwa kutoka hasi 4 hadi 4, na hatua hasi 2 iliyoandikwa na dot.

    Kielelezo\(\PageIndex{8}\)

    Zoezi\(\PageIndex{1}\)

    Plot namba kwenye mstari namba.

    \(1\),\(-1\),\(-4\)

    Jibu

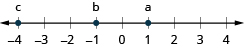
    CNX_BMath_Figure_03_01_010_img.jpg

    Zoezi\(\PageIndex{2}\)

    Plot namba kwenye mstari namba.

    \(-4\),\(4\),\(-1\)

    Jibu

    CNX_BMath_Figure_03_01_011_img.jpg

    Order Chanya na Hasi Hesabu

    Tunaweza kutumia mstari wa nambari kulinganisha na kuagiza namba nzuri na hasi. Kwenda kutoka kushoto kwenda kulia, idadi huongezeka kwa thamani. Kwenda kutoka kulia kwenda kushoto, namba hupungua kwa thamani. Angalia Kielelezo\(\PageIndex{9}\).

    Takwimu hii ni mstari wa nambari. Juu ya mstari wa nambari kuna mshale unaoelezea kuongezeka kwa haki inayoitwa. Chini ya mstari wa nambari kuna mshale unaoelekeza kwenye kichwa cha kushoto kinachopungua.

    Kielelezo\(\PageIndex{9}\)

    Kama tulivyofanya kwa idadi nzuri, tunaweza kutumia alama za kutofautiana ili kuonyesha utaratibu wa idadi nzuri na hasi. Kumbuka kwamba tunatumia nukuu\(a < b\) (kusoma\(a\) ni chini ya\(b\)) wakati\(a\) ni upande wa kushoto wa\(b\) kwenye mstari wa namba. Tunaandika\(a > b\) (kusoma\(a\) ni kubwa kuliko\(b\)) wakati\(a\) ni haki ya\(b\) kwenye mstari wa namba. Hii inavyoonekana kwa idadi\(3\) na\(5\) katika Kielelezo\(\PageIndex{10}\).

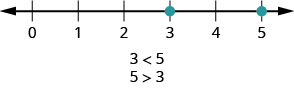
    Takwimu hii ni mstari wa namba na pointi 3 na 5 zilizoandikwa na dots. Chini ya mstari wa nambari ni kauli 3 ni chini ya 5 na 5 ni kubwa kuliko 3.

    Kielelezo\(\PageIndex{10}\): Nambari 3 ni upande wa kushoto wa 5 kwenye mstari wa nambari. Hivyo 3 ni chini ya 5, na 5 ni kubwa kuliko 3.

    Nambari za namba zinazofuata zinaonyesha mifano michache zaidi.

    1. Takwimu hii ni mstari wa namba na pointi 1 na 4 zilizoandikwa na dots.

    \(4\)ni na haki ya\(1\) juu ya mstari idadi, hivyo\(4 > 1\). \(1\)ni upande wa kushoto wa\(4\) kwenye mstari wa simu, hivyo\(1 < 4\).

    1. Takwimu hii ni mstari wa namba na pointi hasi 2 na 1 iliyoandikwa na dots.

    \(-2\)ni upande wa kushoto wa\(1\) kwenye mstari wa simu, hivyo\(−2 < 1\). \(1\)ni na haki ya\(−2\) juu ya mstari idadi, hivyo\(1 > −2\).

    1. Takwimu hii ni mstari wa namba na pointi hasi 3 na hasi 1 iliyoandikwa na dots.

    \(−1\)ni na haki ya\(−3\) juu ya mstari idadi, hivyo\(−1 > −3\). \(−3\)ni upande wa kushoto wa\(−1\) kwenye mstari wa simu, hivyo\(−3 < − 1\).

    Mfano\(\PageIndex{2}\): order the pairs

    Agizo kila moja ya jozi zifuatazo za namba kwa kutumia\(<\) au\(>\):

    1. \(14\)___\(6\)
    2. \(−1\)___\(9\)
    3. \(−1\)___\(−4\)
    4. \(2\)___\(−20\)

    Suluhisho

    Anza kwa kupanga njama namba kwenye mstari wa nambari kama inavyoonekana kwenye Kielelezo\(\PageIndex{11}\).

    Takwimu hii ni mstari wa namba na pointi hasi 20, hasi 4, hasi 1, 2, 6, 9, na 14 iliyoandikwa na dots.

    Kielelezo\(\PageIndex{11}\)

    Linganisha 14 na 6. 14___6
    14 ni haki ya 6 kwenye mstari wa namba. 14> 6
    Linganisha -1 na 9. -1___9
    -1 ni upande wa kushoto wa 9 kwenye mstari wa namba. -1 <9
    Linganisha -1 na -4. -1___-4
    -1 ni upande wa kulia wa -4 kwenye mstari wa namba. -1 > -4
    Linganisha 2 na -20. 2___-20
    2 ni haki ya -20 kwenye mstari wa namba. 2> -20
    Zoezi\(\PageIndex{3}\)

    Agizo kila moja ya jozi zifuatazo za namba kwa kutumia\(<\) au\(>\).

    1. \(15\)___\(7\)
    2. \(−2\)___\(5\)
    3. \(−3\)___\(−7\)
    4. \(5\)___\(−17\)
    Jibu

    \(>\)

    Jibu b

    \(<\)

    Jibu c

    \(>\)

    Jibu d

    \(>\)

    Zoezi\(\PageIndex{4}\)

    Agizo kila moja ya jozi zifuatazo za namba kwa kutumia\(<\) au\(>\).

    1. \(8\)___\(13\)
    2. \(3\)___\(−4\)
    3. \(−5\)___\(−2\)
    4. \(9\)___\(−21\)
    Jibu

    \(<\)

    Jibu b

    \(>\)

    Jibu c

    \(<\)

    Jibu d

    \(>\)

    Kupata Kupinga

    Kwenye mstari wa nambari, namba hasi ni picha ya kioo ya namba nzuri na sifuri katikati. Kwa sababu idadi\(2\) na\(−2\) ni umbali sawa kutoka sifuri, wao ni kuitwa kupinga. Kinyume cha\(2\) ni\(−2\), na kinyume cha\(−2\) ni\(2\) kama inavyoonekana katika Kielelezo\(\PageIndex{12 a}\). Vile vile,\(3\) na\(−3\) ni kinyume kama inavyoonekana katika Kielelezo\(\PageIndex{12 b}\).

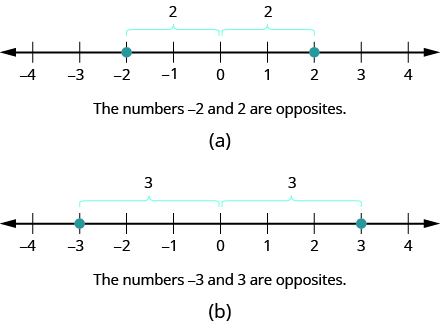
    Takwimu hii inaonyesha mistari miwili ya namba. Ya kwanza ina pointi hasi 2 na chanya 2 kinachoitwa. Chini ya mstari wa kwanza taarifa ni namba hasi 2 na 2 ni kinyume. Nambari ya pili ya nambari ina pointi hasi 3 na 3 zilizoandikwa. Chini ya mstari wa nambari ni taarifa hasi 3 na 3 ni kinyume.

    Kielelezo\(\PageIndex{12}\)

    Ufafanuzi: kinyume

    Kinyume cha namba ni namba ambayo ni umbali sawa kutoka sifuri kwenye mstari wa namba, lakini upande wa pili wa sifuri.

    Mfano\(\PageIndex{3}\):

    Pata kinyume cha kila nambari:

    1. \(7\)
    2. \(−10\)

    Suluhisho

    1. Idadi\(−7\) ni umbali sawa na\(0\) kama\(7\), lakini upande wa pili wa\(0\). Hivyo\(−7\) ni kinyume cha\(7\) kama inavyoonekana katika Kielelezo\(\PageIndex{13}\).

    Takwimu hii ni mstari wa nambari. Pointi hasi 7 na 7 zimeandikwa. Juu ya mstari inavyoonyeshwa umbali kutoka 0 hadi hasi 7 na umbali kutoka 0 hadi 7 ni wote 7.

    Kielelezo\(\PageIndex{13}\)

    1. Idadi\(10\) ni umbali sawa na\(0\) kama\(−10\), lakini upande wa pili wa\(0\). Hivyo\(10\) ni kinyume cha\(−10\) kama inavyoonekana katika Kielelezo\(\PageIndex{14}\).

    Takwimu hii ni mstari wa nambari. Pointi hasi 10 na 10 zimeandikwa. Juu ya mstari inavyoonyeshwa umbali kutoka 0 hadi hasi 10 na umbali kutoka 0 hadi 10 ni wote 10.

    Kielelezo\(\PageIndex{14}\)

    Zoezi\(\PageIndex{5}\)

    Pata kinyume cha kila nambari:

    1. \(4\)
    2. \(−3\)
    Jibu

    \(-4\)

    Jibu b

    \(3\)

    Zoezi\(\PageIndex{6}\)

    Pata kinyume cha kila nambari:

    1. \(8\)
    2. \(−5\)
    Jibu

    \(-8\)

    Jibu b

    \(5\)

    Kinyume Nukuu

    Kama vile neno moja katika Kiingereza linaweza kuwa na maana tofauti, alama sawa katika algebra inaweza kuwa na maana tofauti.

    Maana maalum huwa wazi kwa kuangalia jinsi inavyotumiwa. Umeona ishara “\(−\)”, kwa njia tatu tofauti.

    10 - 4

    Kati ya namba mbili, ishara inaonyesha uendeshaji wa kuondoa.

    Tunasoma 10 - 4 kama 10 minus 4.
    -8

    Mbele ya nambari, ishara inaonyesha namba hasi.

    Tunasoma -8 kama hasi nane.
    -x

    Mbele ya kutofautiana au nambari, inaonyesha kinyume.

    Tunasoma -x kama kinyume cha x.
    - (—2)

    Hapa tuna ishara mbili. Ishara katika mabano inaonyesha kwamba idadi ni hasi 2. Ishara nje ya mabano inaonyesha kinyume.

    Tunasoma - (-2) kama kinyume cha -1.
    Ufafanuzi: Nukuu kinyume

    \(−a\)ina maana kinyume cha idadi\(a\).

    Uthibitisho\(−a\) unasoma kinyume cha\(a\).

    Mfano\(\PageIndex{4}\): simplify

    Kurahisisha:\(−(−6)\).

    Suluhisho

      - (-6)
    Kinyume cha -6 ni 6. 6
    Zoezi\(\PageIndex{7}\)

    Kurahisisha:\(−(−1)\)

    Jibu

    \(1\)

    Zoezi\(\PageIndex{8}\)

    Kurahisisha:\(−(−5)\)

    Jibu

    \(5\)

    Nambari kamili

    Seti ya namba za kuhesabu, kinyume chao, na\(0\) ni seti ya integers.

    Ufafanuzi: integers

    Integers ni kuhesabu idadi, kinyume yao, na sifuri.

    \[\ldots −3, −2, −1, 0, 1, 2, 3 \ldots \nonumber \]

    Lazima tuwe makini sana na ishara wakati wa kutathmini kinyume cha kutofautiana.

    Mfano\(\PageIndex{5}\): evaluate

    Tathmini\(−x\):

    1. lini\(x = 8\)
    2. lini\(x = −8\)

    Suluhisho

    Kutathmini -x wakati x = 8, mbadala 8 kwa x. \(-x\)
    Mbadala\(\textcolor{red}{8}\) kwa ajili ya x. \(-(\textcolor{red}{8})\)
    Kurahisisha. \(-8\)
    Kutathmini -x wakati x = -8, mbadala 8 kwa x. \(-x\)
    Mbadala\(\textcolor{red}{-8}\) kwa ajili ya x. \(-(\textcolor{red}{-8})\)
    Kurahisisha. \(-8\)
    Zoezi\(\PageIndex{9}\)

    Tathmini\(−n\):

    1. lini\(n = 4\)
    2. lini\(n = −4\)
    Jibu

    \(-4\)

    Jibu b

    \(4\)

    Zoezi\(\PageIndex{10}\)

    Tathmini\(−m\):

    1. lini\(m = 11\)
    2. lini\(m = −11\)
    Jibu

    \(-11\)

    Jibu b

    \(11\)

    Kurahisisha Maneno na Thamani kamili

    Tuliona kwamba idadi kama vile\(5\) na\(−5\) ni kinyume kwa sababu wao ni umbali sawa kutoka\(0\) kwenye mstari namba. Wote wawili ni vitengo tano kutoka\(0\). Umbali kati\(0\) na namba yoyote kwenye mstari wa namba inaitwa thamani kamili ya namba hiyo. Kwa sababu umbali hauwezi hasi, thamani kamili ya nambari yoyote haijawahi hasi. Ishara kwa thamani kamili ni mistari miwili ya wima upande wowote wa namba. Hivyo thamani kamili ya\(5\) imeandikwa kama\(|5|\), na thamani kamili ya imeandikwa kama\(|−5|\) inavyoonekana katika Kielelezo\(\PageIndex{15}\).\(−5\)

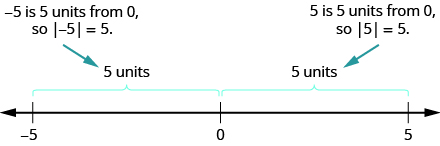
    Takwimu hii ni mstari wa nambari. Pointi hasi 5 na 5 zimeandikwa. Juu ya mstari wa nambari umbali kutoka hasi 5 hadi 0 umeandikwa kama vitengo 5. Pia juu ya mstari wa nambari umbali kutoka 0 hadi 5 umeandikwa kama vitengo 5.

    Kielelezo\(\PageIndex{15}\)

    Ufafanuzi: Thamani kamili

    Thamani kamili ya namba ni umbali wake kutoka\(0\) kwenye mstari wa nambari.

    Thamani kamili ya namba\(n\) imeandikwa kama\(|n|\).

    \[|n| \geq 0\; for\; all\; numbers \nonumber \]

    Mfano 3.6:

    Kurahisisha:

    1. \(|3|\)
    2. \(|−44|\)
    3. \(|0|\)

    Suluhisho

      |3|
    3 ni vitengo 3 kutoka sifuri. 3
      |-44|
    -44 ni 44 vitengo kutoka sifuri. 44
      |0|
    0 tayari iko kwenye sifuri. 0
    Zoezi\(\PageIndex{11}\)

    Kurahisisha:

    1. \(|12|\)
    2. \(− |−28|\)
    Jibu

    \(12\)

    Jibu b

    \(-28\)

    Zoezi 3.12:

    Kurahisisha:

    1. \(|9|\)
    2. \(− |37|\)
    Jibu

    \(9\)

    Jibu b

    \(-37\)