9.1: Punguza na Tumia Mizizi ya Mraba
- Page ID
- 177439
Mwishoni mwa sehemu hii, utaweza:
- Punguza maneno na mizizi ya mraba
- Tathmini mizizi ya mraba
- Mizizi ya mraba takriban
- Punguza maneno ya kutofautiana na mizizi ya mraba
Kabla ya kuanza, fanya jaribio hili la utayari.
- Kurahisisha: ⓐ\(9^2\) ⓑ\((−9)^2\) ⓒ\(−9^2\).
Ikiwa umekosa tatizo hili, tathmini [kiungo]. - Pande zote 3.846 kwa karibu mia moja.
Ikiwa umekosa tatizo hili, tathmini [kiungo]. - Kwa kila namba, kutambua kama ni namba halisi au si namba halisi:
ⓐ\(−\sqrt{100}\) ⓑ\(\sqrt{−100}\).
Ikiwa umekosa tatizo hili, tathmini [kiungo].
Rahisisha maneno na Mizizi ya Mraba
Kumbuka kwamba wakati namba n imeongezeka kwa yenyewe, tunaandika\(n^2\) na kuisoma “n squared.” Kwa mfano,\(15^2\) inasoma kama “mraba 15,” na 225 inaitwa mraba wa 15, tangu\(15^2=225\).
Ikiwa\(n^2=m\), basi m ni mraba wa n.
Wakati mwingine tutahitaji kuangalia uhusiano kati ya namba na mraba wao kwa reverse. Kwa sababu 225 ni mraba wa 15, tunaweza pia kusema kwamba 15 ni mizizi ya mraba ya 225. Nambari ambayo mraba ni m inaitwa mizizi ya mraba ya m.
Ikiwa\(n^2=m\), basi n ni mizizi ya mraba ya m.
Taarifa\((−15)^2=225\) also, so −15 is also a square root of 225. Therefore, both 15 and −15 are square roots of 225.
Kwa hiyo, kila idadi nzuri ina mizizi miwili ya mraba-moja chanya na moja hasi. Nini kama sisi tu alitaka chanya mraba mizizi ya idadi chanya? Ishara kubwa\(\sqrt{m}\), inaashiria mizizi nzuri ya mraba. Mzizi mzuri wa mraba pia huitwa mizizi kuu ya mraba.
Tunatumia pia ishara kubwa kwa mizizi ya mraba ya sifuri. Kwa sababu\(0^2=0\),\(\sqrt{0}=0\). Angalia kwamba sifuri ina mizizi moja tu ya mraba.
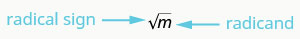
\(\sqrt{m}\)inasoma kama “mizizi ya mraba ya m.”
Ikiwa\(m=n^2\), basi\(\sqrt{m}=n\), kwa\(n \ge 0\).
Mzizi wa mraba wa m\(\sqrt{m}\),, ni idadi nzuri ambayo mraba ni m.
Tangu 15 ni mizizi nzuri ya mraba ya 225, tunaandika\(\sqrt{225}=15\). Fill in Kielelezo kufanya meza ya mizizi ya mraba unaweza kutaja kama unafanya kazi sura hii.

Tunajua kwamba kila nambari nzuri ina mizizi miwili ya mraba na ishara kubwa inaonyesha moja nzuri. Tunaandika\(\sqrt{225}=15\). Ikiwa tunataka kupata mizizi ya mraba hasi ya nambari, tunaweka hasi mbele ya ishara kubwa. Kwa mfano,\(−\sqrt{225}=−15\).
Kurahisisha:
- \(\sqrt{36}\)
- \(\sqrt{196}\)
- \(−\sqrt{81}\)
- \(−\sqrt{289}\).
- Jibu
-
1.
\[\begin{array}{ll} {}&{\sqrt{36}}\\ {\text{Since} 6^2=36}&{6}\\ \end{array}\]
2.
\[\begin{array}{ll} {}&{\sqrt{196}}\\ {\text{Since} 14^2=196}&{14}\\ \end{array}\]
3.
\[\begin{array}{ll} {}&{−\sqrt{81}}\\ {\text{The negative is in front of the radical sign}}&{−9}\\ \end{array}\]
4.
\[\begin{array}{ll} {}&{−\sqrt{289}}\\ {\text{The negative is in front of the radical sign}}&{−17}\\ \end{array}\]
Kurahisisha:
- \(−\sqrt{49}\)
- \(\sqrt{225}\).
- Jibu
-
- -7
- 15
kurahisisha:
- \(\sqrt{64}\)
- \(−\sqrt{121}\).
- Jibu
-
- 8
- -11
Kurahisisha:
- \(\sqrt{−169}\)
- \( −\sqrt{64}\)
- Jibu
-
1.
\[\begin{array}{ll} {}&{\sqrt{−169}}\\ {\text{There is no real number whose square is} s−169}&{\sqrt{−169} \text{is not a real number.}}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{−\sqrt{64}}\\ {\text{The negative is in front of the radical sign}}&{−8}\\ \end{array}\]
Kurahisisha:
- \(\sqrt{−196}\)
- \(−\sqrt{81}\).
- Jibu
-
- si idadi halisi
- —9
Kurahisisha:
- \(−\sqrt{49}\)
- \(\sqrt{ −121}\).
- Jibu
-
- -7
- si idadi halisi
Wakati wa kutumia utaratibu wa shughuli ili kurahisisha maneno ambayo ina mizizi ya mraba, tunachukua radical kama ishara ya kikundi.
Kurahisisha:
- \(\sqrt{25} +\sqrt{144}\)
- \(\sqrt{25+144}\).
- Jibu
-
1.
\[\begin{array}{ll} {}&{\sqrt{25} +\sqrt{144}}\\ {\text{Use the order of operations}}&{5+12}\\ {\text{Simplify.}}&{17}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{\sqrt{25+144}}\\ {\text{Simplify under the radical sign.}}&{\sqrt{169}}\\ {\text{Simplify.}}&{13}\\ \end{array}\]
Angalia majibu tofauti katika sehemu 1 na 2!
Kurahisisha:
- \(\sqrt{9}+\sqrt{16}\)
- \(\sqrt{9+16}\).
- Jibu
-
- 7
- 5
Kurahisisha:
- \(\sqrt{64+225}\)
- \(\sqrt{64}+\sqrt{225}\).
- Jibu
-
- 17
- 23
Tathmini Mizizi ya Mraba
Hadi sasa tumezingatia mizizi ya mraba ya namba kamili za mraba. Mizizi ya mraba ya namba nyingine sio namba nzima. Angalia Jedwali hapa chini.
| Idadi | Mizizi ya mraba |
|---|---|
| 4 | \(\sqrt{4}=2\) |
| 5 | \(\sqrt{5}\) |
| 6 | \(\sqrt{6}\) |
| 7 | \(\sqrt{7}\) |
| 8 | \(\sqrt{8}\) |
| 9 | \(\sqrt{9}=3\) |
Mizizi ya mraba ya namba kati ya 4 na 9 lazima iwe kati ya namba mbili za mfululizo 2 na 3, na sio namba nzima. Kulingana na muundo katika meza hapo juu, tunaweza kusema kwamba\(\sqrt{5}\) lazima iwe kati ya 2 na 3. Kutumia alama za usawa, tunaandika:
\(2<\sqrt{5}<3\)
Tathmini\(\sqrt{60}\) kati ya namba mbili za mfululizo.
- Jibu
-
Fikiria namba kamili za mraba karibu na 60. Fanya meza ndogo ya mraba huu kamili na mizizi yao ya mraba.
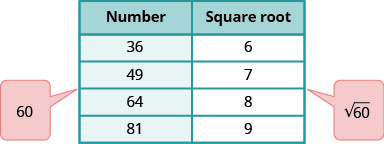
Machapisho 60 kati ya mraba mbili mfululizo kamili. 
\(\sqrt{60}\)ni kati ya mizizi yao ya mraba. 
Tathmini mizizi ya mraba\(\sqrt{38}\) kati ya namba mbili za mfululizo.
- Jibu
-
\(6<\sqrt{38}<7\)
Tathmini mizizi ya mraba\(\sqrt{84}\) kati ya namba mbili za mfululizo.
- Jibu
-
\(9<\sqrt{84}<10\)
Mizizi ya Mraba
Kuna mbinu za hisabati kwa takriban mizizi ya mraba, lakini siku hizi watu wengi hutumia kikokotoo ili kuzipata. Pata\(\sqrt{x}\) ufunguo kwenye calculator yako. Utatumia ufunguo huu kwa mizizi ya mraba takriban.
Unapotumia calculator yako ili kupata mizizi ya mraba ya namba ambayo si mraba kamili, jibu unayoona sio mzizi wa mraba halisi. Ni makadirio, sahihi na idadi ya tarakimu inavyoonekana kwenye kuonyesha calculator yako ya. ishara kwa makadirio ni\(\approx\) na ni kusoma 'takriban.'
Tuseme calculator yako ina kuonyesha tarakimu 10. Ungependa kuona kwamba
\(\sqrt{5} \approx 2.236067978\)
Kama tulitaka pande zote\(\sqrt{5}\) kwa maeneo mawili decimal, tunaweza kusema
\(\sqrt{5} \approx 2.24\)
Je, tunajua maadili haya ni makadirio na si maadili halisi? Angalia nini kinatokea wakati sisi mraba yao:
\[\begin{array}{c} {(2.236067978)^2=5.000000002}\\ {(2.24)^2=5.0176}\\ \end{array}\]
Mraba yao ni karibu na 5, lakini si sawa sawa na 5.
Kutumia ufunguo wa mizizi ya mraba kwenye calculator na kisha kuzunguka kwenye sehemu mbili za decimal, tunaweza kupata:
\[\begin{array}{c} {\sqrt{4}=2}\\ {\sqrt{5} \approx 2.24}\\ {\sqrt{6} \approx 2.45}\\ {\sqrt{7} \approx 2.65}\\ {\sqrt{8} \approx 2.83}\\ {\sqrt{9}=3}\\ \end{array}\]
Pande zote\(\sqrt{17}\) kwa maeneo mawili ya decimal.
- Jibu
-
\[\begin{array}{ll} {}&{\sqrt{17}}\\ {\text{Use the calculator square root key.}}&{4.123105626...}\\ {\text{Round to two decimal places.}}&{4.12}\\ {}&{\sqrt{17} \approx 4.12} \end{array}\]
Pande zote\(\sqrt{11}\) kwa maeneo mawili ya decimal.
- Jibu
-
\(\approx 3.32\)
Pande zote\(\sqrt{13}\) kwa maeneo mawili ya decimal.
- Jibu
-
\(\approx 3.61\)
Punguza maneno ya kutofautiana na Mizizi ya Mraba
Nini kama tuna kupata mizizi mraba wa kujieleza na variable? Fikiria\(\sqrt{9x^2}\). Je, unaweza kufikiria maneno ambayo mraba ni\(9x^2\)?
\[\begin{array}{cc} {(?)^2=9x^2}&{}\\ {(3x)^2=9x^2}&{\text{so} \sqrt{9x^2}=3x}\\ \end{array}\]
Tunapotumia ishara kali kuchukua mizizi ya mraba ya kujieleza kutofautiana, tunapaswa kutaja kwamba x≥ 0x≥ 0 ili kuhakikisha tunapata mizizi ya mraba kuu.
Hata hivyo, katika sura hii sisi kudhani kwamba kila variable katika kujieleza mraba-mizizi inawakilisha idadi zisizo hasi na hivyo hatuwezi kuandika\(x \ge 0\) karibu na kila radical.
Nini kuhusu mizizi ya mraba ya mamlaka ya juu ya vigezo? Fikiria juu ya Power Mali ya Exponents sisi kutumika katika Sura ya 6.
\((a^m)^n=a^{m·n}\)
Kama sisi mraba\(a^m\), exponent itakuwa 2m.
\((a^m)^2=a^{2m}\)
Hii inatusaidia kuchukua mizizi ya mraba? Hebu tuangalie wachache:
\[\begin{array}{cc} {\sqrt{25u^8}=5u^4}&{\text{Because} (5u^4)^2=25u^8}\\ {\sqrt{16r^{20}}=4r^{10}}&{\text{Because} (4r^{10})^2=16r^{20}}\\ {\sqrt{196q^{36}}=14q^{18}}&{\text{Because} (14r^{18})^2=196q^{36}}\\ \end{array}\]
Kurahisisha:
- \(\sqrt{x^6}\)
- \(\sqrt{y^{16}}\)
- Jibu
-
1.
\[\begin{array}{ll} {}&{\sqrt{x^6}}\\ {\text{Since} (x^3)^2=x^6}&{x^3}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{\sqrt{y^{16}}}\\ {\text{Since} (y^8)^2=y^{16}}&{y^8}\\ \end{array}\]
Kurahisisha:
- \(\sqrt{y^8}\)
- \(\sqrt{z^{12}}\).
- Jibu
-
- \(y^4\)
- \(z^6\)
Kurahisisha:
- \(\sqrt{m^4}\)
- \(\sqrt{b^{10}}\).
- Jibu
-
- \(m^2\)
- \(b^5\)
Kurahisisha:\(\sqrt{16n^2}\)
- Jibu
-
\[\begin{array}{ll} {}&{\sqrt{16n^2}}\\ {\text{Since} (4n)^2=16n^2}&{4n}\\ \end{array}\]
Kurahisisha:\(\sqrt{64x^2}\).
- Jibu
-
\(8x\)
Kurahisisha:\(\sqrt{169y^2}\).
- Jibu
-
\(13y\)
Kurahisisha:\(−\sqrt{81c^2}\).
- Jibu
-
\[\begin{array}{ll} {}&{−\sqrt{81c^2}}\\ {\text{Since} (9c)^2=81c^2}&{−9c}\\ \end{array}\]
Kurahisisha:\(−\sqrt{121y^2}\).
- Jibu
-
\(−11y\)
Kurahisisha:\(−\sqrt{100p^2}\).
- Jibu
-
\(−10p\)
Kurahisisha:\(\sqrt{36x^{2}y^{2}}\).
- Jibu
-
\[\begin{array}{ll} {}&{\sqrt{36x^{2}y^{2}}}\\ {\text{Since} (6xy)^2=\sqrt{36x^{2}y^{2}}}&{6xy}\\ \end{array}\]
Kurahisisha:\(\sqrt{100a^{2}b^{2}}\).
- Jibu
-
10ab
Kurahisisha:\(\sqrt{225m^{2}n^{2}}\).
- Jibu
-
15mn
Kurahisisha:\(\sqrt{64p^{64}}\).
- Jibu
-
\[\begin{array}{ll} {}&{\sqrt{64p^{64}}}\\ {\text{Since} (8p^8)^2=\sqrt{64p^{64}}}&{8p^8}\\ \end{array}\]
Kurahisisha:\(\sqrt{49x^{30}}\).
- Jibu
-
\(7x^{15}\)
Kurahisisha:\(\sqrt{81w^{36}}\)
- Jibu
-
\(9w^{18}\)
Kurahisisha:\(\sqrt{121a^{6}b^{8}}\)
- Jibu
-
\[\begin{array}{ll} {}&{\sqrt{121a^{6}b^{8}}}\\ {\text{Since} (11a^{3}b^{4})^2=\sqrt{121a^{6}b^{8}}}&{11a^{3}b^{4}}\\ \end{array}\]
Kurahisisha:\(\sqrt{169x^{10}y^{14}}\)
- Jibu
-
\(13x^{5}y^{7}\)
Kurahisisha:\(\sqrt{144p^{12}q^{20}}\)
- Jibu
-
\(\sqrt{12p^{6}q^{10}}\)
Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi na mizizi ya mraba.
- Mizizi ya mraba
Dhana muhimu
- Kumbuka kwamba mizizi ya mraba ya nambari hasi sio namba halisi.
- Kila nambari nzuri ina mizizi miwili ya mraba, moja chanya na moja hasi. Mzizi mzuri wa mraba wa idadi nzuri ni mizizi kuu ya mraba.
- Tunaweza kukadiria mizizi ya mraba kwa kutumia viwanja vilivyo karibu.
- Tunaweza takriban mizizi ya mraba kwa kutumia calculator.
- Tunapotumia ishara kali kuchukua mizizi ya mraba ya kujieleza kutofautiana, tunapaswa kutaja kwamba\(x \ge 0\) ili kuhakikisha tunapata mizizi kuu ya mraba.
faharasa
- mraba wa idadi
-
- Ikiwa\(n^2=m\), basi m ni mraba wa n
- mizizi ya mraba ya idadi
-
- Ikiwa\(n^2=m\), basi n ni mizizi ya mraba ya m
- nukuu ya mizizi ya mraba
-
- Ikiwa\(m=n^2\), basi\(\sqrt{m}=n\). Tunasoma\(\sqrt{m}\) kama 'mizizi ya mraba ya m. '


