Skip to main content
Global

1.7: Ongeza na Ondoa sehemu

  1. Last updated
  2. Save as PDF
  • Page ID
    178075

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Ongeza au uondoe sehemu ndogo na denominator ya kawaida
    • Ongeza au uondoe sehemu ndogo na madhehebu tofauti
    • Tumia utaratibu wa shughuli ili kurahisisha sehemu ndogo
    • Tathmini maneno ya kutofautiana na sehemu ndogo
    Kumbuka

    Utangulizi wa kina zaidi wa mada yaliyofunikwa katika sehemu hii inaweza kupatikana katika sura ya Prealgebra, Sehemu ndogo.

    Ongeza au Ondoa sehemu ndogo na Denominator ya kawaida

    Wakati sisi kuzidisha sehemu, sisi tu kuzidisha numerators na kuzidisha denominators haki moja kwa moja hela. Ili kuongeza au kuondoa sehemu ndogo, lazima iwe na denominator ya kawaida.

    SEHEMU YA KUONGEZA NA KUONDOA

    Kama\(a,b\), na\(c\) ni idadi ambapo\(c\neq 0\), basi

    \[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c} \quad \text{and} \quad \dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a - b}{c}\]

    Ili kuongeza au kuondoa sehemu ndogo, ongeza au uondoe nambari na uweke matokeo juu ya denominator ya kawaida.

    Manipulative Hisabati

    Kufanya shughuli za Hisabati za Manipulative “Uongeze wa Fraction Model” na “Model Fraction Ondoa” itasaidia kuendeleza uelewa bora wa kuongeza na kuondoa sehemu ndogo.

    Zoezi\(\PageIndex{1}\)

    Pata jumla:\(\dfrac{x}{3} + \dfrac{2}{3}\).

    Jibu

    \[\begin{array} {ll} {} &{\dfrac{x}{3} + \dfrac{2}{3}} \\ {\text{Add the numerators and place the sum over the common denominator}} &{\dfrac{x + 2}{3}} \end{array}\]

    Zoezi\(\PageIndex{2}\)

    Pata jumla:\(\dfrac{x}{4} + \dfrac{3}{4}\).

    Jibu

    \(\dfrac{x + 3}{4}\)

    Zoezi\(\PageIndex{3}\)

    Pata jumla:\(\dfrac{y}{8} + \dfrac{5}{8}\).

    Jibu

    \(\dfrac{y + 5}{8}\)

    Zoezi\(\PageIndex{4}\)

    Pata tofauti:\(-\dfrac{23}{24} - \dfrac{13}{24}\)

    Jibu

    \[\begin{array} {ll} {} &{-\dfrac{23}{24} - \dfrac{13}{24}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-23 - 13}{24}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Simplify.}} &{\dfrac{-36}{24}} \\ {\text{Simplify. Remember, }-\dfrac{a}{b} = \dfrac{-a}{b}} &{-\dfrac{3}{2}} \end{array}\]

    Zoezi\(\PageIndex{5}\)

    Pata tofauti:\(-\dfrac{19}{28} - \dfrac{7}{28}\)

    Jibu

    \(-\dfrac{26}{28}\)

    Zoezi\(\PageIndex{6}\)

    Pata tofauti:\(-\dfrac{27}{32} - \dfrac{1}{32}\)

    Jibu

    \(-\dfrac{7}{8}\)

    Zoezi\(\PageIndex{7}\)

    Pata tofauti:\(-\dfrac{10}{x} - \dfrac{4}{x}\)

    Jibu

    \[\begin{array} {ll} {} &{-\dfrac{10}{x} - \dfrac{4}{x}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-14}{x}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Rewrite with the sign in front of the fraction.}} &{-\dfrac{14}{x}} \end{array}\]

    Zoezi\(\PageIndex{8}\)

    Pata tofauti:\(-\dfrac{9}{x} - \dfrac{7}{x}\)

    Jibu

    \(-\dfrac{16}{x}\)

    Zoezi\(\PageIndex{9}\)

    Pata tofauti:\(-\dfrac{17}{a} - \dfrac{5}{a}\)

    Jibu

    \(-\dfrac{22}{a}\)

    Sasa tutafanya mfano ambao una kuongeza na kuondoa.
    Zoezi\(\PageIndex{10}\)

    Kurahisisha:\(\dfrac{3}{8} + (-\dfrac{5}{8}) - \dfrac{1}{8}\)

    Jibu

    \[\begin{array} {ll} {\text{Add and Subtract fractions — do they have a }} &{\frac{3}{8} + (-\frac{5}{8}) - \frac{1}{8}} \\ {\text{common denominator? Yes.}} &{} \\ {\text{Add and subtract the numerators and place }} &{\frac{3 + (-5) - 1}{8}} \\ {\text{the result over the common denominator.}} &{} \\ {\text{Simplify left to right.}} &{\frac{-2 - 1}{8}} \\ {\text{Simplify.}} &{-\frac{3}{8}} \end{array}\]

    Zoezi\(\PageIndex{11}\)

    Kurahisisha:\(\dfrac{2}{9} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)

    Jibu

    \(-1\)

    Zoezi\(\PageIndex{12}\)

    Kurahisisha:\(\dfrac{2}{5} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)

    Jibu

    \(-\dfrac{2}{3}\)

    Ongeza au Ondoa sehemu na Denominators tofauti

    Kama tulivyoona, kuongeza au kuondoa sehemu ndogo, denominators yao lazima iwe sawa. Denominator ya kawaida (LCD) ya sehemu mbili ni idadi ndogo ambayo inaweza kutumika kama denominator ya kawaida ya sehemu ndogo. LCD ya sehemu mbili ni ndogo zaidi ya kawaida (LCM) ya denominators yao.

    DENOMINATOR ISIYO YA KAWAIDA

    Denominator ya kawaida (LCD) ya sehemu mbili ni ndogo zaidi ya kawaida (LCM) ya denominators yao.

    Kumbuka

    Kufanya shughuli za Hisabati za Manipulative “Kutafuta Denominator ya kawaida” itakusaidia kuendeleza uelewa bora wa LCD.

    Baada ya kupata denominator ya kawaida ya sehemu mbili, tunabadilisha sehemu ndogo kwa sehemu sawa na LCD. Kuweka hatua hizi pamoja inatuwezesha kuongeza na kuondoa sehemu kwa sababu madhehebu yao yatakuwa sawa!

    Zoezi\(\PageIndex{13}\)

    Ongeza:\(\dfrac{7}{12} + \dfrac{5}{18}\)

    Jibu

    Katika takwimu hii, tuna meza na maelekezo upande wa kushoto, vidokezo au maelezo katikati, na taarifa za hisabati upande wa kulia. Kwenye mstari wa kwanza, tuna “Hatua ya 1. Je, wana denominator ya kawaida? Hapana — Andika upya kila sehemu na LCD (denominator angalau kawaida).” Kwa haki ya hili, tuna taarifa “Hapana. Kupata LCD 12, 18.” Kwa haki ya hii, tuna 12 sawa mara 2 mara 3 na 18 sawa mara 2 mara 3. LCD ni hivyo mara 2 mara 2 mara 3, ambayo ni sawa na 36. Kama ladha nyingine, tuna “Badilisha katika sehemu sawa na LCD,. Je, si kurahisisha sehemu sawa! Kama wewe, itabidi kupata nyuma sehemu ya awali na kupoteza denominator kawaida!” Kwa haki ya hili, tuna 7/12 pamoja na 5/18, ambayo inakuwa wingi (mara 7 mara 3) juu ya wingi (mara 12 3) pamoja na wingi (mara 5 2) juu ya wingi (mara 18 2), ambayo inakuwa 21/36 pamoja na 10/36.Hatua inayofuata inasoma “Hatua ya 2. Ongeza au uondoe sehemu ndogo.” Hint inasoma “Ongeza.” Na tuna 31/36.Hatua ya mwisho inasoma “Hatua ya 3. Kurahisisha, kama inawezekana.” maelezo inasoma “Kwa sababu 31 ni idadi mkuu, haina sababu sawa na 36. Jibu ni rahisi.”

    Zoezi\(\PageIndex{14}\)

    Ongeza:\(\dfrac{7}{12} + \dfrac{11}{15}\)

    Jibu

    \(\dfrac{79}{60}\)

    Zoezi\(\PageIndex{15}\)

    Ongeza:\(\dfrac{7}{12} + \dfrac{11}{15}\)

    Jibu

    \(\dfrac{103}{60}\)

    ONGEZA AU ONDOA SEHEMU NDOGO.
    1. Je, wana denominator ya kawaida?
      • Ndiyo-nenda hatua ya 2.
      • Hapana-Andika upya kila sehemu na LCD (denominator angalau ya kawaida). Kupata LCD. Badilisha kila sehemu katika sehemu sawa na LCD kama denominator yake.
    2. Ongeza au uondoe sehemu ndogo.
    3. Kurahisisha, ikiwa inawezekana.

    Wakati wa kutafuta sehemu sawa zinazohitajika ili kuunda denominators ya kawaida, kuna njia ya haraka ya kupata nambari tunayohitaji kuzidisha nambari zote na denominator. Njia hii kazi kama sisi kupatikana LCD kwa factoring katika primes.

    Angalia mambo ya LCD na kisha kila safu juu ya mambo hayo. Sababu za “kukosa” za kila denominator ni namba tunayohitaji.

    idadi 12 ni factored katika 2 mara 2 mara 3 na nafasi ya ziada baada ya 3, na idadi 18 ni factored katika 2 mara 3 mara 3 na nafasi ya ziada kati ya 2 na 3 kwanza. Kuna mishale inayoelezea nafasi hizi za ziada ambazo zimewekwa alama “sababu zisizopotea.” LCD ni alama kama mara 2 mara 3 mara 3, ambayo ni sawa na 36. Nambari zinazounda LCD ni sababu kutoka 12 na 18, na mambo ya kawaida yanahesabiwa mara moja tu (yaani, 2 ya kwanza na ya kwanza 3).
    Kielelezo:\(\PageIndex{1}\)

    Katika Zoezi\(\PageIndex{13}\), LCD, 36, ina mambo mawili ya 2 na mambo mawili ya 3.

    Nambari 12 ina mambo mawili ya 2 lakini moja tu ya 3—hivyo ni “kukosa” moja 3—tunazidisha namba na denominator kwa 3.

    Nambari 18 inakosa sababu moja ya 2—hivyo tunazidisha nambari na denominator kwa 2.

    Tutatumia njia hii tunapoondoa sehemu ndogo katika Zoezi\(\PageIndex{16}\).

    Zoezi\(\PageIndex{16}\)

    Ondoa:\(\dfrac{7}{15} - \dfrac{19}{24}\)

    Jibu

    Je, sehemu ndogo zina denominator ya kawaida? Hapana, kwa hiyo tunahitaji kupata LCD.

    Kupata LCD. .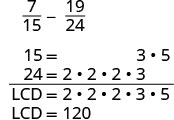  
    Kumbuka, 15 ni “kukosa” mambo matatu ya 2 na 24 ni “kukosa” 5 kutokana na sababu za LCD. Kwa hiyo tunazidisha 8 katika sehemu ya kwanza na 5 katika sehemu ya pili ili kupata LCD.  
    Andika upya kama sehemu ndogo sawa na LCD. .
    Kurahisisha. .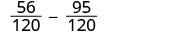
    Ondoa. \(-\dfrac{39}{120}\)
    Angalia ili uone kama jibu linaweza kuwa rahisi. \(-\dfrac{13\cdot3}{40\cdot3}\)
    Wote 39 na 120 wana sababu ya 3.  
    Kurahisisha. \(-\dfrac{13}{40}\)

    Je, si kurahisisha sehemu sawa! Kama wewe, itabidi kupata nyuma sehemu ya awali na kupoteza denominator kawaida!

    Zoezi\(\PageIndex{17}\)

    Ondoa:\(\dfrac{13}{24} - \dfrac{17}{32}\)

    Jibu

    \(\dfrac{1}{96}\)

    Zoezi\(\PageIndex{18}\)

    Ondoa:\(\dfrac{7}{15} - \dfrac{19}{24}\)

    Jibu

    \(\dfrac{75}{224}\)

    Katika mfano unaofuata, moja ya sehemu ndogo ina variable katika nambari yake. Kumbuka kwamba tunafanya hatua sawa na wakati nambari zote mbili ni namba.

    Zoezi\(\PageIndex{19}\)

    Ongeza:\(\dfrac{3}{5} + \dfrac{x}{8}\)

    Jibu

    Sehemu ndogo zina madhehebu tofauti.

      .
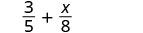
    Kupata LCD. .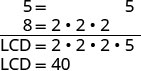  
    Andika upya kama sehemu ndogo sawa na LCD. .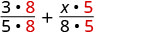
    Kurahisisha. .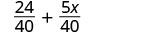
    Ongeza. .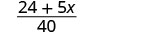

    Kumbuka, tunaweza tu kuongeza kama maneno:\(24\) na\(5x\) si kama maneno.

    Zoezi\(\PageIndex{20}\)

    Ongeza:\(\dfrac{y}{6} + \dfrac{7}{9}\)

    Jibu

    \(\dfrac{3y + 14}{18}\)

    Zoezi\(\PageIndex{21}\)

    Ongeza:\(\dfrac{x}{6} + \dfrac{7}{15}\)

    Jibu

    \(\dfrac{15x + 42}{153}\)

    Sasa tuna shughuli zote nne kwa sehemu ndogo. Jedwali\(\PageIndex{1}\) linafupisha shughuli za sehemu.

    Kuzidisha sehemu Sehemu ya Idara
    \(\dfrac{a}{b}\cdot \dfrac{c}{d} = \dfrac{ac}{bd}\)
    Kuzidisha nambari na kuzidisha denominators    		 \(\dfrac{a}{b}\div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\)
    Panua sehemu ya kwanza kwa usawa wa pili.
    Sehemu ya kuongeza Fraction Ondoa
    \(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\)
    Ongeza nambari na uweke jumla juu ya denominator ya kawaida.    		 \(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\)
    Ondoa nambari na uweke tofauti juu ya denominator ya kawaida.
    Ili kuzidisha au kugawanya sehemu ndogo, na LCD haihitajiki. Ili kuongeza au kuondoa sehemu ndogo, LCD inahitajika.
    Jedwali\(\PageIndex{1}\)
    Zoezi\(\PageIndex{22}\)

    Kurahisisha:

    1. \(\dfrac{5x}{6} - \dfrac{3}{10}\)
    2. \(\dfrac{5x}{6}\cdot \dfrac{3}{10}\).
    Jibu

    Kwanza uulize, “Kazi ni nini?” Mara baada ya kutambua operesheni ambayo itaamua kama tunahitaji denominator ya kawaida. Kumbuka, tunahitaji denominator ya kawaida ili kuongeza au kuondoa, lakini si kuzidisha au kugawanya.

    1. Operesheni ni nini? Uendeshaji ni kuondoa.

    \[\begin{array} {ll} {\text{Do the fractions have a common denominator? No.}} &{\frac{5x}{6} - \frac{3}{10}} \\ {\text{Rewrite each fractions as an equivalent fraction with the LCD.}} &{\frac{5x\cdot 5}{6\cdot 5} - \frac{3\cdot3}{10\cdot3}} \\ {} &{\frac{25x}{30} - \frac{9}{30}} \\{\text{Subtract the numerators and place the difference over the}} &{\frac{25x - 9}{30}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify, if possible. There are no common factors.}} &{} \\ {\text{The fraction is simplified.}} &{} \end{array}\]

    2. Operesheni ni nini? Kuzidisha.

    \[\begin{array} {ll} {} &{\frac{5x}{6}\cdot \frac{3}{10}} \\ {\text{To multiply fractions, multiply the numerators and multiply}} &{\frac{5x\cdot 3}{6\cdot 10}} \\ {\text{the denominators}} &{} \\{\text{Rewrite, showing common factors.}} &{\frac{\not 5 x\cdot\not3}{2\cdot\not3\cdot2\cdot\not5}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify.}} &{\frac{x}{4}} \end{array}\]

    Zoezi\(\PageIndex{23}\)

    Kurahisisha:

    1. \(\dfrac{3a}{4} - \dfrac{8}{9}\)
    2. \(\dfrac{3a}{4}\cdot\dfrac{8}{9}\)
    Jibu
    1. \(\dfrac{27a - 32}{36}\)
    2. \(\dfrac{2a}{3}\)
    Zoezi\(\PageIndex{24}\)

    Kurahisisha:

    1. \(\dfrac{4k}{5} - \dfrac{1}{6}\)
    2. \(\dfrac{4k}{5}\cdot\dfrac{1}{6}\)
    Jibu
    1. \(\dfrac{24k - 5}{30}\)
    2. \(\dfrac{2k}{15}\)

    Tumia Utaratibu wa Uendeshaji ili kurahisisha Fractions Complex

    Tumeona kwamba sehemu tata ni sehemu ambayo nambari au denominator ina sehemu. Bar ya sehemu inaonyesha mgawanyiko. Sisi kilichorahisisha sehemu tata\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) kwa kugawa\(\dfrac{3}{4}\) na\(\dfrac{5}{8}\).

    Sasa tutaangalia sehemu ndogo ambapo namba au denominator ina maneno ambayo yanaweza kuwa rahisi. Kwa hiyo sisi kwanza tunapaswa kurahisisha kabisa nambari na denominator tofauti kwa kutumia utaratibu wa shughuli. Kisha tunagawanya nambari na denominator.

    Zoezi\(\PageIndex{25}\): How to simplify complex fractions

    Kurahisisha:\(\dfrac{(\frac{1}{2})^{2}}{4 + 3^{2}}\)

    Jibu

    Katika takwimu hii, tuna meza na maelekezo kwenye kauli za kushoto na za hisabati upande wa kulia. Kwenye mstari wa kwanza, tuna “Hatua ya 1. Kurahisisha nambari. Kumbuka nusu moja ya mraba inamaanisha mara nusu moja.” Kwa haki ya hili, tuna kiasi (1/2) kilichopangwa kila kiasi (4 pamoja na 3 mraba). Kisha, tuna 1/4 juu ya wingi (4 pamoja na 3 squared).
    Hatua ya 2.
    Hatua ya mwisho ni “Hatua ya 3. Gawanya nambari kwa denominator. Kurahisisha kama inawezekana. Kumbuka, kumi na tatu sawa kumi na tatu juu ya 1.” Kwa haki tuna 1/4 imegawanywa na 13. Kisha tuna 1/4 mara 1/13, ambayo ni sawa 1/52.

    Zoezi\(\PageIndex{26}\)

    Kurahisisha:\(\dfrac{(\frac{1}{3})^{2}}{2^{3} + 2}\)

    Jibu

    \(\dfrac{1}{90}\)

    Zoezi\(\PageIndex{27}\)

    Kurahisisha:\(\dfrac{1 + 4^{2}}{(\frac{1}{4})^{2}}\)

    Jibu

    \(272\)

    KURAHISISHA SEHEMU NDOGO.
    1. Kurahisisha nambari.
    2. Kurahisisha denominator.
    3. Gawanya nambari kwa denominator. Kurahisisha kama inawezekana.
    Zoezi\(\PageIndex{28}\)

    Kurahisisha:\(\dfrac{\frac{1}{2} + \frac{2}{3}}{\frac{3}{4} - \frac{1}{6}}\)

    Jibu

    \[\begin{array} {ll} {} &{\frac{(\frac{1}{2} + \frac{2}{3})}{(\frac{3}{4} - \frac{1}{6})}} \\ {\text{Simplify the numerator (LCD = 6) and simplify the denominator (LCD = 12).}} &{\frac{(\frac{3}{6} + \frac{4}{6})}{(\frac{9}{12} - \frac{2}{12})}} \\ {\text{Simplify.}} &{\frac{(\frac{7}{6})}{(\frac{7}{12})}} \\{\text{Divide the numerator by the denominator.}} &{\frac{7}{6}\div\frac{7}{12}} \\ {\text{Simplify.}} &{\frac{7}{6}\cdot\frac{12}{7}} \\ {\text{Divide out common factors.}} &{\frac{7\cdot6\cdot2}{6\cdot7}} \\ {\text{Simplify.}} &{2} \end{array}\]

    Zoezi\(\PageIndex{29}\)

    Kurahisisha:\(\dfrac{\frac{1}{3} + \frac{1}{2}}{\frac{3}{4} - \frac{1}{3}}\)

    Jibu

    \(2\)

    Zoezi\(\PageIndex{30}\)

    Kurahisisha:\(\dfrac{\frac{2}{3} - \frac{1}{2}}{\frac{1}{4} + \frac{1}{3}}\)

    Jibu

    \(\dfrac{2}{7}\)

    Tathmini Maneno ya kutofautiana na FRACTIONS

    Tumepima maneno kabla, lakini sasa tunaweza kutathmini maneno na sehemu ndogo. Kumbuka, kutathmini maneno, sisi badala ya thamani ya kutofautiana katika kujieleza na kisha kurahisisha.

    Zoezi\(\PageIndex{31}\)

    Tathmini\(x + \dfrac{1}{3}\) wakati

    1. \(x = -\dfrac{1}{3}\)
    2. \(x = -\dfrac{3}{4}\)
    Jibu

    1. Kutathmini\(x + \dfrac{1}{3}\) wakati\(x = -\dfrac{1}{3}\), badala\(-\dfrac{1}{3}\) ya\(x\) katika kujieleza.

      .
    . .
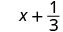
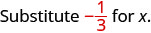
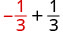
    Kurahisisha. \(0\)


    2. Kutathmini\(x + \dfrac{1}{3}\) wakati\(x = -\dfrac{3}{4}\), badala\(-\dfrac{3}{4}\) ya\(x\) katika kujieleza.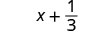
      .
    . .
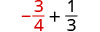
    Andika upya kama sehemu ndogo sawa na LCD, 12. .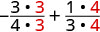
    Kurahisisha. .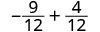
    Ongeza. \(-\dfrac{5}{12}\)
    Zoezi\(\PageIndex{32}\)

    Tathmini\(x + \dfrac{3}{4}\) wakati

    1. \(x = -\dfrac{7}{4}\)
    2. \(x = -\dfrac{5}{4}\)
    Jibu
    1. \(-1\)
    2. \(-\dfrac{1}{2}\)
    Zoezi\(\PageIndex{33}\)

    Tathmini\(y + \dfrac{1}{2}\) wakati

    1. \(y = \dfrac{2}{3}\)
    2. \(y = -\dfrac{3}{4}\)
    Jibu
    1. \(\dfrac{7}{6}\)
    2. \(-\dfrac{1}{12}\)
    Zoezi\(\PageIndex{34}\)

    Tathmini\(-\dfrac{5}{6} - y\) wakati\(y = -\dfrac{2}{3}\)

    Jibu
      .
    . .
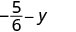
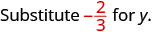
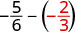
    Andika upya kama sehemu ndogo sawa na LCD,\(6\). .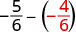
    Ondoa. .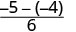
    Kurahisisha. \(-\dfrac{1}{6}\)
    Zoezi\(\PageIndex{35}\)

    Tathmini\(y + \dfrac{1}{2}\) wakati\(y = \dfrac{2}{3}\)

    Jibu

    \(-\dfrac{1}{4}\)

    Zoezi\(\PageIndex{36}\)

    Tathmini\(y + \dfrac{1}{2}\) wakati\(y = \dfrac{2}{3}\)

    Jibu

    \(-\dfrac{17}{8}\)

    Zoezi\(\PageIndex{37}\)

    Tathmini\(2x^{2}y\)\(x = \dfrac{1}{4}\) lini na\(y = -\dfrac{2}{3}\).

    Jibu

    Badilisha maadili katika maneno.

      \(2x^{2}y\)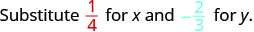
    . .
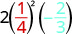
    Kurahisisha watetezi kwanza. \(2(\frac{1}{16})(-\frac{2}{3})\)
    Kuzidisha. Gawanya mambo ya kawaida. Angalia tunaandika\(16\) kama\(2\cdot2\cdot4\) ili iwe rahisi kuondoa \(-\frac{\not2\cdot1\cdot\not2}{\not2\cdot\not2\cdot4\cdot3}\)
    Kurahisisha. \(-\frac{1}{12}\)
    Zoezi\(\PageIndex{38}\)

    Tathmini\(3ab^{2}\)\(a = -\dfrac{2}{3}\) lini na\(b = -\dfrac{1}{2}\).

    Jibu

    \(-\dfrac{1}{2}\)

    Zoezi\(\PageIndex{39}\)

    Tathmini\(4c^{3}d\)\(c = -\dfrac{1}{2}\) lini na\(d = -\dfrac{4}{3}\).

    Jibu

    \(\dfrac{2}{3}\)

    Mfano unaofuata utakuwa na vigezo tu, hakuna mara kwa mara.

    Zoezi\(\PageIndex{40}\)

    Tathmini\(\dfrac{p + q}{r}\) wakati\(p = -4, q = -2\), na\(r = 8\).

    Jibu

    Kutathmini\(\dfrac{p + q}{r}\) wakati\(p = -4, q = -2\), na\(r = 8\), sisi badala ya maadili katika kujieleza.

      \(\dfrac{p + q}{r}\)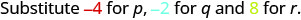
    . .
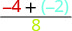
    Ongeza kwenye nambari ya kwanza. \(\dfrac{-6}{8}\)
    Kurahisisha. \(-\dfrac{3}{4}\)
    Zoezi\(\PageIndex{41}\)

    Tathmini\(\dfrac{a+b}{c}\) wakati\(a = -8, b = -7\), na\(c = 6\).

    Jibu

    \(-\dfrac{5}{2}\)

    Zoezi\(\PageIndex{42}\)

    Tathmini\(\dfrac{x+y}{z}\) wakati\(x = 9, y = -18\), na\(z = -6\).

    Jibu

    \(\dfrac{3}{2}\)

    Dhana muhimu

    • Sehemu Aidha na Ondoa: Kama\(a, b\), na\(c\) ni idadi ambapo\(c\neq 0\), kisha
      \(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\) na\(\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}\)
      Kuongeza au Ondoa sehemu, kuongeza au Ondoa nambari na mahali matokeo juu ya denominator ya kawaida.
    • Mkakati wa Kuongeza au Kuondoa FRACTIONS
      1. Je, wana denominator ya kawaida?
        Ndiyo-nenda hatua ya 2.
        Hapana—Andika upya kila sehemu na LCD (Denominator isiyo ya kawaida). Kupata LCD. Badilisha kila sehemu katika sehemu sawa na LCD kama denominator yake.
      2. Ongeza au uondoe sehemu ndogo.
      3. Kurahisisha, ikiwa inawezekana. Ili kuzidisha au kugawanya sehemu ndogo, LCD haihitajiki. Ili kuongeza au kuondoa sehemu ndogo, LCD inahitajika.
    • Kurahisisha Fractions Complex
      1. Kurahisisha nambari.
      2. Kurahisisha denominator.
      3. Gawanya nambari kwa denominator. Kurahisisha kama inawezekana.