8.6: Migongano ya Misa ya Point katika Vipimo viwili

Last updated
Save as PDF

Page ID: 183200

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Jadili migongano miwili ya mwelekeo kama ugani wa uchambuzi mmoja wa mwelekeo.
Kufafanua raia uhakika.
Kupata kujieleza kwa ajili ya uhifadhi wa kasi pamoja x -axis na y -axis.
Eleza migongano ya elastic ya vitu viwili na molekuli sawa.
Kuamua ukubwa na mwelekeo wa kasi ya mwisho kutokana kasi ya awali, na kueneza angle.

Katika sehemu mbili zilizopita, tulizingatia migongano moja-dimensional tu; wakati wa migongano kama hiyo, kasi zinazoingia na zinazotoka ziko kwenye mstari huo. Lakini vipi kuhusu migongano, kama vile wale kati ya mipira ya billiard, ambayo vitu vinaenea upande? Hizi ni migongano mbili-dimensional, na tutaona kwamba utafiti wao ni ugani wa uchambuzi moja-dimensional tayari kuwasilishwa. Njia iliyochukuliwa (sawa na mbinu katika kujadili kinematics mbili-dimensional na mienendo) ni kuchagua mfumo rahisi wa kuratibu na kutatua mwendo katika vipengele pamoja na axes perpendicular. Kutatua mwendo huzaa matatizo mawili ya mwelekeo mmoja ili kutatuliwa wakati huo huo.

Matatizo moja yanayotokana na migongano mbili-dimensional ni kwamba vitu vinaweza kugeuka kabla au baada ya mgongano wao. Kwa mfano, kama skaters mbili barafu ndoano silaha kama wao kupita kwa kila mmoja, wao spin katika miduara. Hatuwezi kuzingatia mzunguko huo mpaka baadaye, na kwa sasa tunapanga mambo ili hakuna mzunguko unaowezekana. Ili kuepuka mzunguko, tunazingatia tu kueneza kwa raia wa uhakika - yaani, chembe zisizo na muundo ambazo haziwezi kuzunguka au kuzunguka.

Tunaanza kwa kudhani kwamba\(F_{net} = 0,\) ili kasi\(p\) ihifadhiwe. Mgongano rahisi ni moja ambayo moja ya chembe hupumzika. (Angalia Kielelezo.) Chaguo bora kwa ajili ya mfumo wa kuratibu ni moja na mhimili sambamba na kasi ya chembe zinazoingia, kama inavyoonekana katika Kielelezo. Kwa sababu kasi imehifadhiwa, vipengele vya kasi pamoja\(x-\) na\(y-\) shoka (\(p_x \)na\(p_y\)) pia zitahifadhiwa, lakini kwa mfumo wa kuratibu uliochaguliwa,\(p_y\) ni awali sifuri na\(p_x\) ni kasi ya chembe inayoingia. Wote ukweli kurahisisha uchambuzi. (Hata kwa mawazo ya kurahisisha ya raia wa uhakika, chembe moja awali katika mapumziko, na mfumo rahisi wa kuratibu, bado tunapata ufahamu mpya katika asili kutokana na uchambuzi wa migongano mbili-dimensional.)

Mpira wa rangi ya zambarau wa molekuli m1 huenda kwa kasi V 1 kuelekea upande wa kulia pamoja na mwelekeo wa X. Mpira wa machungwa wa molekuli m 2 ni awali wakati wa kupumzika. kasi jumla ni kasi inayomilikiwa na mpira wa rangi ya zambarau tu. Baada ya mgongano zambarau mpira hatua kwa kasi v 1prime katika chanya X Y ndege kufanya angle theta 1 na x mhimili na mpira machungwa hatua katika X Y ndege chini x mhimili kufanya angle theta 2 na x mhimili. kasi jumla itakuwa jumla ya kasi ya zambarau mpira P1 mkuu na machungwa mpira p 2 mkuu. Katika mgongano mbili-dimensional pia kasi kabla na baada ya mgongano bado ni sawa. — Kielelezo\(\PageIndex{1}\): Mgongano wa pande mbili na mfumo wa kuratibu uliochaguliwa ili\(m_2\) uwe awali unapumzika na\(v_1\) unafanana na\(x\) -axis. Mfumo huu wa kuratibu wakati mwingine huitwa mfumo wa kuratibu maabara, kwa sababu majaribio mengi ya kutawanya yana shabaha ambayo ni stationary katika maabara, huku chembe zinatawanyika kutoka humo ili kuamua chembe zinazofanya shabaha na jinsi zinavyofungwa pamoja. Chembe haziwezi kuzingatiwa moja kwa moja, lakini kasi yao ya awali na ya mwisho ni.

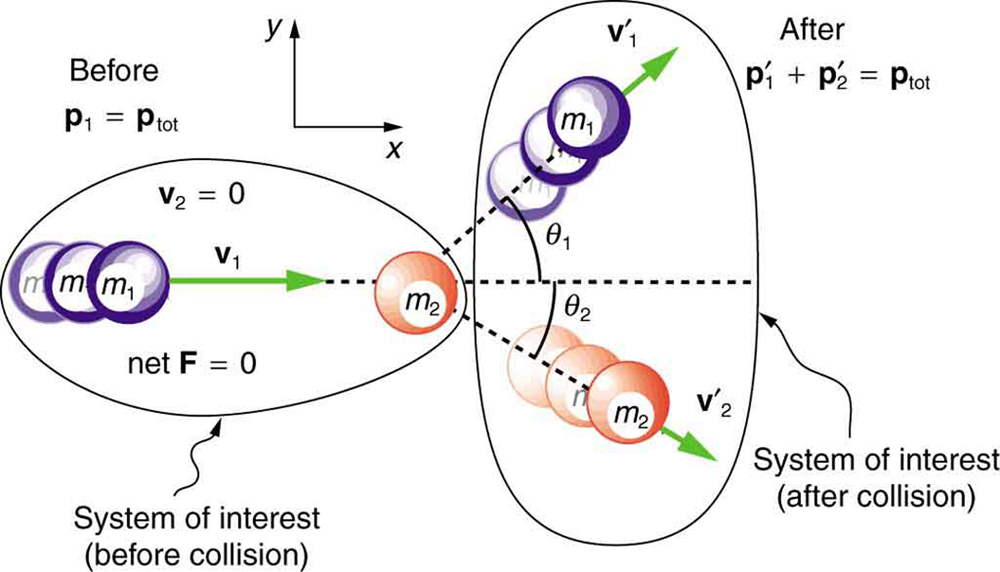
Pamoja\(x\) -axis, equation kwa ajili ya uhifadhi wa kasi ni\[p_{1x} + p_{2x} = p'_{1x} + p'_{2x} .\]

Ambapo scripts zinaashiria chembe na axes na primes zinaashiria hali baada ya mgongano. Kwa upande wa raia na kasi, equation hii ni\[m_1v_1 + m_2v_{2x} = m_1v'_{1x} + m_2v'_{2x}.\]

Lakini kwa sababu chembe 2 ni awali katika mapumziko, equation hii inakuwa\[m_1v_1 = m_1v'_{1x} + m_2v'_{2x}.\]

Vipengele vya kasi kando ya\(x\) -axis vina fomu\(v \, cos \, \theta\). Kwa sababu chembe 1 awali hatua pamoja\(x\) -axis, tunaona\(v_{1x} = v_1\).

Hifadhi ya kasi pamoja\(x\) -mhimili anatoa equation zifuatazo\[ m_1v_1 = m_1v'_1 \, cos \, \theta_1 + m_2v'_2 \, cos \, \theta_2,\] ambapo\(\theta_1\) na\(\theta_2\) ni kama inavyoonekana katika Kielelezo.

Uhifadhi wa kasi Pamoja na x-axis

\[ m_1v_1 = m_1v'_1 \, cos \, \theta_1 + m_2v'_2 \, cos \, \theta_2\]

Pamoja na\(y\) -axis, equation kwa ajili ya uhifadhi wa kasi ni\[p_{1y} + p_{2y} = p'_{1y} + p'_{2y},\] au\[m_1v_1 + m_2v_{2y} = m_1v'_{1y} + m_2v'_{2y}.\]

Lakini\(v_{1y} \) ni sifuri, kwa sababu chembe 1 awali hatua pamoja\(x\) -axis. Kwa sababu chembe 2 ni awali katika mapumziko, pia\(v_{2y}\) ni sifuri. Equation kwa ajili ya uhifadhi wa kasi kando ya\(y\) mhimili inakuwa\[0 = m_1v'_{1y} + m_2v'_{2y}.\]

Vipengele vya kasi kando ya\(y\) -axis vina fomu\(v \, sin \, \theta\).

Hivyo, uhifadhi wa kasi kando ya\(y\) mhimili hutoa equation ifuatayo:\[0 = m_1v'_{1y} \, sin \, \theta_1 + m_2v'_{2y} \, sin \, \theta_2.\]

Uhifadhi wa kasi Pamoja na y-axis

\[0 = m_1v'_{1y} \, sin \, \theta_1 + m_2v'_{2y} \, sin \, \theta_2.\]

Equations ya uhifadhi wa kasi pamoja\(x\) -axis na\(y\) -axis ni muhimu sana katika kuchunguza migongano mbili-dimensional ya chembe, ambapo moja ya awali ni stationary (hali ya kawaida ya maabara). Lakini equations mbili zinaweza kutumika tu kupata haijulikani mbili, na hivyo data nyingine inaweza kuwa muhimu wakati majaribio ya mgongano yanatumiwa kuchunguza asili katika ngazi ya subatomic.

Mfano\(\PageIndex{1}\): Determining the Final Velocity of an Unseen Object from the

Kusambaza Kitu Kingine

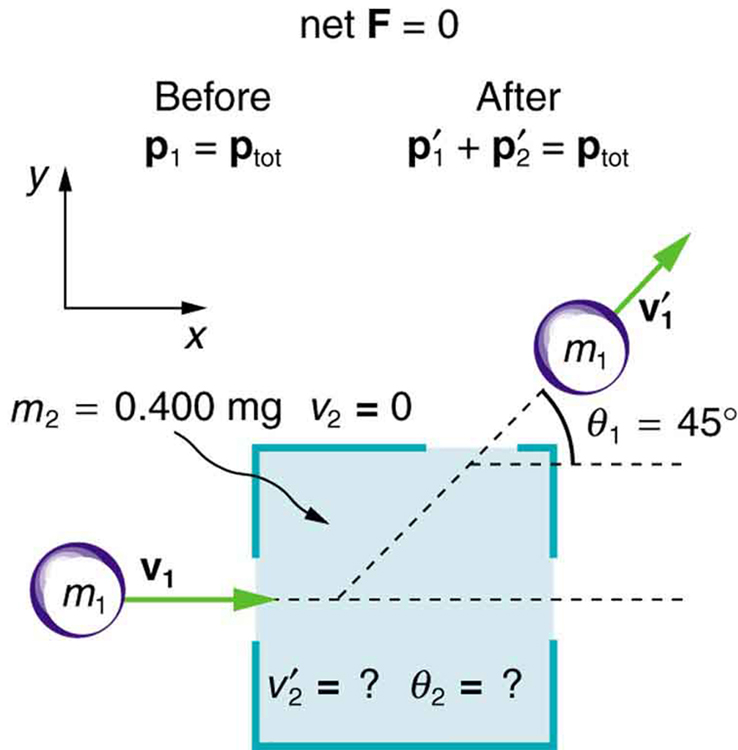
Tuseme jaribio linalofuata linafanyika. Kitu cha kilo 0.250\((m_1)\) kinawekwa kwenye uso usio na msuguano ndani ya chumba cha giza, ambako hupiga kitu cha awali kilichowekwa na uzito wa kilo 0.400\((m_2)\). Kitu cha kilo 0.250 kinatokea kutoka kwenye chumba kwa pembe ya\(45^o\) mwelekeo wake unaoingia.Kasi ya kitu cha kilo 0.250 ni awali 2.00 m/s na ni 1.50 m/s baada ya mgongano. Tumia ukubwa na mwelekeo wa kasi\((v'_2\) na kitu\(\theta_2)\) cha kilo 0.400-baada ya mgongano.

Mkakati

Kasi huhifadhiwa kwa sababu uso hauwezi msuguano. Mfumo wa kuratibu unaoonyeshwa kwenye Kielelezo ni moja ambayo\(m_2\) ni ya awali ya kupumzika na kasi ya awali ni sawa na\(x\) -axis, ili uhifadhi wa kasi kando ya\(x\) - na\(y\) -axes inatumika. Kila kitu kinajulikana katika equations hizi isipokuwa\(v'_2\) na\(\theta_2\), ambayo ni kiasi ambacho tunataka kupata. Tunaweza kupata unknowns mbili kwa sababu tuna milinganyo mbili huru: equations kuelezea uhifadhi wa kasi katika\(x\) - na\(y\) -maelekezo.

Suluhisho

Kutatua\(m_1v_1 = m_1v'_1 \, cos \, \theta_1 + m_2v'_2 \, cos \, \theta_2\) kwa\(v'_2 \, cos \, \theta_2\) na\(0 = m_1v'_{1y} \, sin \, \theta_1 + m_2v'_{2y} \, sin \, \theta_2\) kwa\(v'_2 \, sin \, \theta_2\) na kuchukua uwiano mavuno equation (ambayo\(\theta_2\) ni kiasi tu haijulikani). Kutumia utambulisho\(\left(tan \, \theta = \frac{sin \, \theta}{cos \, \theta} \right) \), tunapata

\[tan \, \theta_2 = \dfrac{v'_1 \, sin \, \theta_1}{v'_1 \, cos \, \theta_1 - v_1}.\]

Kuingia maadili inayojulikana katika equation uliopita inatoa

\[tan \, \theta_2 = \dfrac{(1.50 \, m/s)(0.7071)}{(1.50 \, m/s)(0.7071) - 2.00 \, m/s} = -1.129.\]

Hivyo,\[\theta_2 = tan^{-1}9-1.129) = 311.5^o \approx 312^o.\]

Angles hufafanuliwa kama chanya katika mwelekeo wa saa moja kwa moja, hivyo angle hii inaonyesha kwamba\(m_2\) ni kutawanyika kwa haki katika Kielelezo, kama inavyotarajiwa (angle hii iko katika roboduara ya nne). Aidha equation kwa\(x\) - au\(y\) -axis sasa inaweza kutumika kutatua kwa\(v_2\), lakini equation mwisho ni rahisi kwa sababu ina masharti machache.

\[v'_2 = - \left( \dfrac{0.250 \, kg}{0.400 \, kg} \right) (1.50 \, m/s) \left(\dfrac{0.7071}{-0.7485} \right).\]

Hivyo,\[v'_2 = 0.886 \, m/s.\]

Majadiliano

Ni muhimu kuhesabu nishati ya ndani ya kinetic ya mfumo huu wa kitu mbili kabla na baada ya mgongano. (Hesabu hii imesalia kama tatizo la mwisho wa sura.) Ikiwa unafanya hesabu hii, utapata kwamba nishati ya ndani ya kinetic ni ndogo baada ya mgongano, na hivyo mgongano hauna inelastic. Aina hii ya matokeo hufanya mwanafizikia kutaka kuchunguza mfumo zaidi.

mpira zambarau ya molekuli m1 na kasi v hatua moja katika mwelekeo sahihi katika chumba giza. Ni collides na kitu ya molekuli m mbili ya thamani sifuri uhakika nne zero milligrams ambayo awali ilikuwa katika mapumziko na kisha majani chumba giza kutoka upande wa juu wa kulia na kufanya angle ya digrii arobaini na tano na usawa na kwa kasi v mkuu mmoja. Nguvu ya nje ya nje kwenye mfumo ni sifuri. Kasi kabla na baada ya mgongano bado ni sawa. kasi v mbili mkuu wa molekuli m mbili na angle theta mbili ingekuwa kufanya na usawa baada ya mgongano si kupewa. — Kielelezo\(\PageIndex{2}\): Mgongano unaofanyika katika chumba giza unachunguzwa katika Mfano. Kitu kinachoingia\(m_1\) kinatawanyika na kitu cha awali kilichowekwa. Masi tu ya kitu cha stationary\(m_2\) inajulikana. Kwa kupima angle na kasi ambayo\(m_1\) inatoka kwenye chumba, inawezekana kuhesabu ukubwa na mwelekeo wa kasi ya kitu cha awali cha kituo baada ya mgongano.

Migongano ya elastic ya vitu viwili na Misa sawa

Baadhi ya hali ya kuvutia hutokea wakati vitu viwili vinavyogongana vina wingi sawa na mgongano ni elastic. Hali hii ni karibu na kesi na mipira ya billiard iliyopigana, na hasa kesi na migongano ya chembe ya subatomic. Hivyo tunaweza kupata picha ya akili ya mgongano wa chembe subatomic kwa kufikiri juu ya billiards (au bwawa). (Rejea Kielelezo kwa raia na pembe.) Kwanza, mgongano wa elastic huhifadhi nishati ya ndani ya kinetic. Tena, hebu kudhani kitu 2\(m_2\) ni awali katika mapumziko. Kisha, nishati ya ndani ya kinetic kabla na baada ya mgongano wa vitu viwili ambavyo vina raia sawa ni

\[\dfrac{1}{2}mv_1^2 = \dfrac{1}{2}mv_1^{'2} + \dfrac{1}{2}mv_2^{'2}.\]

Kwa sababu raia ni sawa,\(m_1 = m_2 = m\). Algebraic kudanganywa (kushoto kwa msomaji) ya uhifadhi wa kasi katika\(x\) - na\(y\) -maelekezo inaweza kuonyesha kwamba

\[\dfrac{1}{2}mv_1^2 = \dfrac{1}{2}mv_1^{'2} + \dfrac{1}{2}mv_2^{'2} + mv'_1 v'_2 \, cos (\theta_1 - \theta_2).\]

(Kumbuka kwamba\(\theta_2\) ni hasi hapa.) Milinganyo miwili iliyotangulia inaweza kuwa ya kweli tu ikiwa\[mv'_1 v'_2 \, cos (\theta_1 - \theta_2) = 0.\]

Kuna njia tatu ambazo neno hili linaweza kuwa sifuri. Wao ni

\(v'_1 = 0\): mgongano wa kichwa-juu; mpira unaoingia unaacha;

\(v'_2 = 0\): hakuna mgongano; mpira unaoingia unaendelea bila kuathiriwa

Yote tatu ya njia hizi ni matukio ya kawaida katika billiards na bwawa, ingawa wengi wetu kujaribu kuepuka pili. Ikiwa unacheza pool ya kutosha, utaona kwamba pembe kati ya mipira iko karibu sana na 90º baada ya mgongano, ingawa itatofautiana na thamani hii ikiwa mpango mkubwa wa spin umewekwa kwenye mpira. (Spin kubwa hubeba nishati ya ziada na kiasi kinachoitwa kasi ya angular, ambayo lazima pia ihifadhiwe.) Dhana kwamba kueneza kwa mipira ya billiard ni elastic ni busara kulingana na usahihi wa matokeo matatu ambayo hutoa. Dhana hii pia ina maana kwamba, kwa makadirio nzuri, kasi ni kuhifadhiwa kwa mfumo mbili mpira katika billiards na pool. Matatizo hapa chini ya kuchunguza sifa hizi na nyingine za migongano mbili-dimensional.

UHUSIANO NA FIZIKIA YA NYUKLIA

Mbili-dimensional mgongano majaribio umebaini mengi ya kile tunachokijua kuhusu chembe subatomic, kama tutaona katika Matumizi ya Matibabu ya Fizikia ya nyuklia na Fizikia Ernest Rutherford, kwa mfano, aligundua asili ya kiini cha atomiki kutokana na majaribio hayo.

Muhtasari

Njia ya migongano mbili-dimensional ni kuchagua mfumo rahisi wa kuratibu na kuvunja mwendo ndani ya vipengele pamoja na axes perpendicular. Chagua mfumo wa kuratibu na x-axis sambamba na kasi ya chembe inayoingia.
Mbili-dimensional migongano ya raia uhakika ambapo molekuli 2 awali katika mapumziko kuhifadhi kasi pamoja mwelekeo wa awali wa wingi 1 (x-axis), alisema\(m_1v_1=m_1v′_1cosθ_1+m_2v′_2cosθ_2\) na kando ya mwelekeo perpendicular mwelekeo wa awali (y-mhimili) alisema na\(0=m_1v′_1y+m_2v′2_y\).
Kinetic ya ndani kabla na baada ya mgongano wa vitu viwili ambavyo vina raia sawa ni
\(\frac{1}{2}mv_1^2=\frac{1}{2}mv′_1^2+\frac{1}{2}mv′_2^2+mv′_1v′_2cos(θ_1−θ_2)\).
Misa ya uhakika ni chembe zisizo na muundo ambazo haziwezi kuzunguka.

faharasa

kumweka raia: chembe structureless na hakuna mzunguko au spin