3.4: Mwendo wa Projectile
- Page ID
- 183392
Malengo ya kujifunza
Mwishoni mwa sehemu hii, utaweza:
- Tambua na kuelezea mali ya projectile, kama vile kuongeza kasi kutokana na mvuto, upeo, urefu wa juu, na trajectory.
- Kuamua eneo na kasi ya projectile kwa pointi tofauti katika trajectory yake.
- Tumia kanuni ya uhuru wa mwendo ili kutatua matatizo ya mwendo wa projectile.
Mwendo wa projectile ni mwendo wa kitu kilichoponywa au kilichopangwa ndani ya hewa, chini ya kuongeza kasi ya mvuto. Kitu kinachoitwa projectile, na njia yake inaitwa trajectory yake. Mwendo wa vitu vya kuanguka, kama kufunikwa katika Misingi ya kutatua matatizo kwa Kinematiki ya One-Dimensional, ni aina rahisi ya mwelekeo wa projectile ambayo hakuna harakati ya usawa. Katika sehemu hii, tunazingatia mwendo wa projectile mbili-dimensional, kama ile ya soka au kitu kingine ambacho upinzani wa hewa hauna maana.
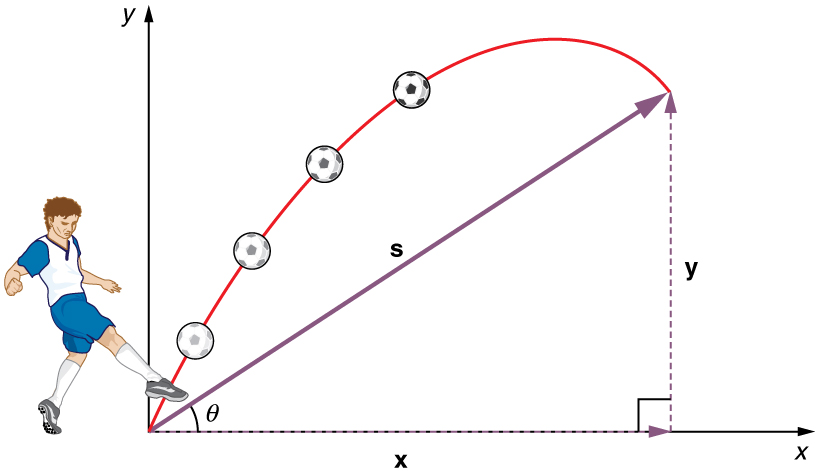
Ukweli muhimu zaidi kukumbuka hapa ni kwamba mwendo pamoja na axes perpendicular ni huru na hivyo inaweza kuchambuliwa tofauti. Ukweli huu ulijadiliwa katika Kinematics katika Vipimo viwili: Utangulizi, ambapo mwendo wa wima na usawa ulionekana kuwa huru. Funguo la kuchunguza mwendo wa projectile mbili-dimensional ni kuivunja katika mwendo mbili, moja pamoja na mhimili usawa na nyingine pamoja na wima. (Uchaguzi huu wa axes ni busara zaidi, kwa sababu kuongeza kasi kutokana na mvuto ni wima - hivyo, hakutakuwa na kasi kwenye mhimili usio na usawa wakati upinzani wa hewa hauna maana.) Kama ilivyo desturi, tunaita mhimili usio na usawa x -axis na mhimili wima y -axis. Kielelezo unaeleza nukuu kwa ajili ya makazi yao, ambapo\(\displaystyle s\) ni defined kuwa makazi ya jumla\(\displaystyle x\) na na\(\displaystyle y\) ni sehemu yake pamoja shoka usawa na wima, kwa mtiririko huo. Ukubwa wa wadudu hawa ni s, x, na y. (Kumbuka kuwa katika sehemu ya mwisho tulitumia notation\(\displaystyle A\) kuwakilisha vector na vipengele\(\displaystyle A_x\) na\(\displaystyle A_y\). Kama sisi kuendelea format hii, tutakuwa wito makazi yao\(\displaystyle s\) na vipengele\(\displaystyle s_x\) na\(\displaystyle s_y\). Hata hivyo, ili kurahisisha notation, sisi tu kuwakilisha vectors sehemu kama\(\displaystyle x\) na\(\displaystyle y\).)
Bila shaka, kuelezea mwendo tunapaswa kukabiliana na kasi na kuongeza kasi, pamoja na uhamisho. Lazima tupate vipengele vyao pamoja na x- na y -axes, pia. Tutadhani nguvu zote isipokuwa mvuto (kama vile upinzani wa hewa na msuguano, kwa mfano) ni duni. Vipengele vya kuongeza kasi ni rahisi sana:\(\displaystyle a_y=–g=–9.80 m/s^2\) (. (Kumbuka kuwa ufafanuzi huu unafikiri kwamba mwelekeo wa juu hufafanuliwa kama mwelekeo mzuri. Ikiwa unapanga mfumo wa kuratibu badala ya kuwa mwelekeo wa chini ni chanya, kisha kuongeza kasi kutokana na mvuto inachukua thamani nzuri.) Kwa sababu mvuto ni wima,\(\displaystyle a_x=0\). Kasi zote mbili ni mara kwa mara, hivyo equations kinematic inaweza kutumika.
MAPITIO YA EQUATIONS KINEMATIC (MARA KWA MARA)
\(\displaystyle x=x_0+\bar{v}t\)
\(\displaystyle \bar{v}=\frac{v_0+v}{2}\)
\(\displaystyle v=v_0+at\)
\(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\)
\(\displaystyle v^2=v^2_0+2a(x−x_0)\).
Kutokana na mawazo haya, hatua zifuatazo zinatumiwa kuchambua mwendo wa projectile:
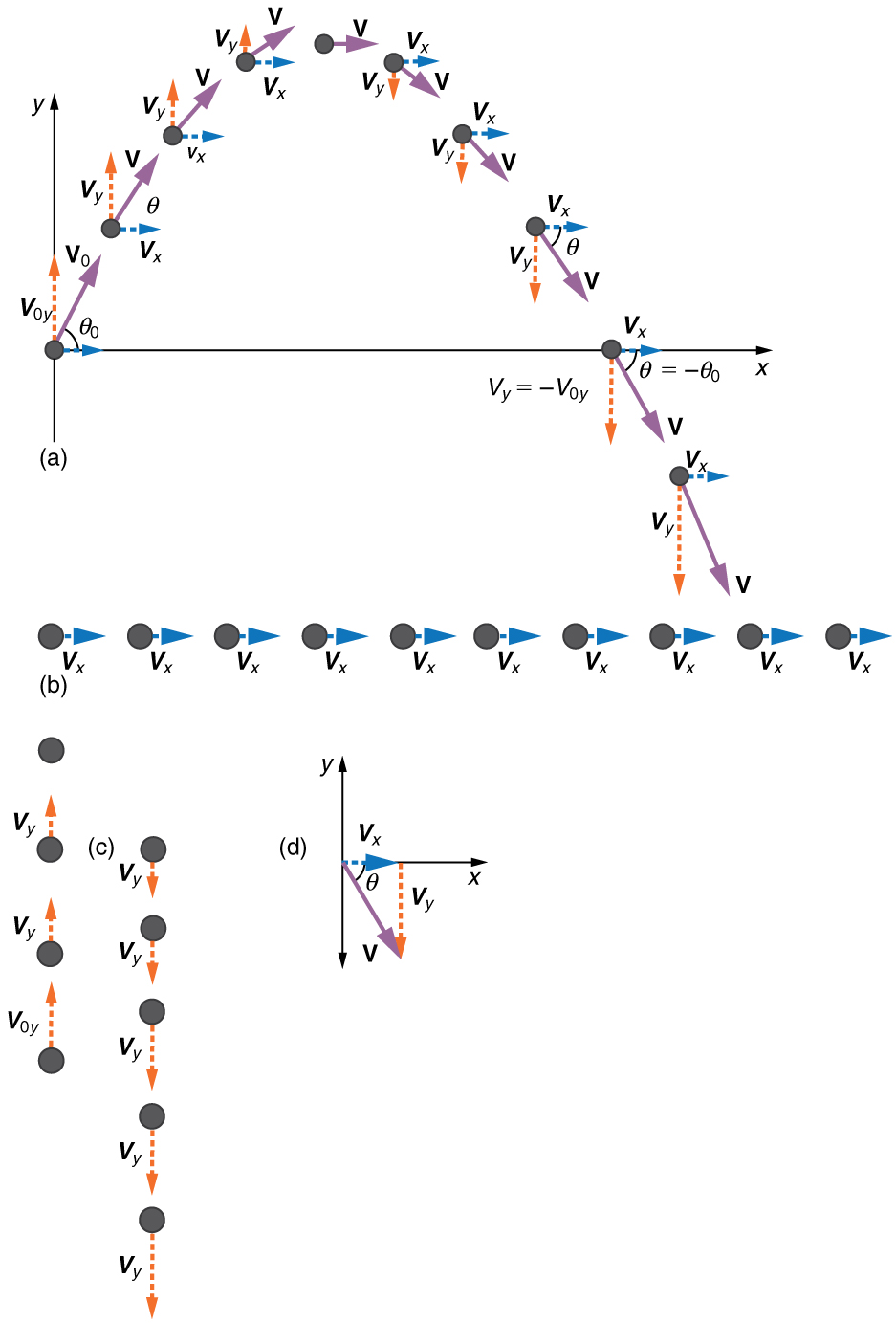
Hatua ya 1. Tatua au kuvunja mwendo ndani ya vipengele vya usawa na wima pamoja na x- na y-axes. Axes hizi ni perpendicular, hivyo\(\displaystyle A_x=Acosθ\) na\(\displaystyle A_y=Asinθ\) hutumiwa. Ukubwa wa vipengele vya uhamisho\(\displaystyle s\) pamoja na axes hizi ni\(\displaystyle x\) na\(\displaystyle y\). Ukubwa wa vipengele vya kasi\(\displaystyle v\) ni\(\displaystyle v_x=vcosθ\) na\(\displaystyle v_y=vsinθ\), wapi ukubwa wa kasi na η\(\displaystyle v\) ni mwelekeo wake, kama inavyoonekana kwenye Mchoro. Maadili ya awali yanatajwa na usajili 0, kama kawaida.
Hatua ya 2. Tumia mwendo kama mwendo wa kujitegemea wa mwelekeo mmoja, moja ya usawa na wima mwingine. Ulinganisho wa kinematic kwa mwendo usio na usawa na wima huchukua fomu zifuatazo:
\(\displaystyle \text{Horizontal Motion}(a_x=0)\)
\(\displaystyle x=x_0+v_xt\)
\(\displaystyle v_x=v_{0x}=v_x=\text{velocity is a constant}\).
\(\displaystyle \text{Vertical Motion(assuming positive is up}a_y=−g=−9.80m/s^2)\)
\(\displaystyle y=y_0+\frac{1}{2}(v_{0y}+v_y)t\)
\(\displaystyle v_y=v_{0y}−gt\)
\(\displaystyle y=y_0+v_{0y}t−\frac{1}{2}gt^2\)
\(\displaystyle v^2_y=v^2_{0y}−2g(y−y_0)\).
Hatua ya 3. Kutatua kwa unknowns katika mwendo mbili tofauti-moja usawa na moja wima. Kumbuka kuwa variable tu ya kawaida kati ya mwendo ni wakati t. Taratibu za kutatua tatizo hapa ni sawa na kinematics moja-dimensional na zinaonyeshwa katika mifano ya kutatuliwa hapa chini.
Hatua ya 4. Rejesha tena mwendo mbili ili kupata uhamisho wa jumla\(\displaystyle s\) na kasi\(\displaystyle v\). Kwa sababu x - na y - mwendo ni perpendicular, sisi kuamua wadudu hawa kwa kutumia mbinu ilivyoainishwa katika Vector Aidha na Ondoa: Analytical Mbinu\(\displaystyle A=\sqrt{A^2_x+A^2_y}\) na kuajiri na\(\displaystyle θ=tan^{−1}(A_y/A_x)\) katika fomu ifuatayo, ambapo\(\displaystyle θ\) ni mwelekeo wa uhamisho\(\displaystyle s\) na\(\displaystyle θ_v\) ni mwelekeo wa kasi\(\displaystyle v\):
Jumla ya makazi na kasi
\(\displaystyle s=\sqrt{x^2+y^2}\)
\(\displaystyle θ=tan^{−1}(y/x)\)
\(\displaystyle v=\sqrt{v^2_x+v^2_y}\)
\(\displaystyle θ_v=tan^{−1}(v_y/v_x)\).
Mfano\(\displaystyle \PageIndex{1}\): A Fireworks Projectile Explodes High and Away
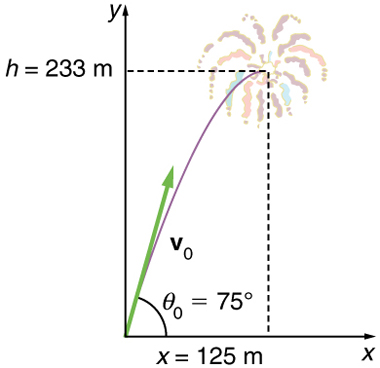
Wakati wa maonyesho ya fireworks, shell hupigwa ndani ya hewa na kasi ya awali ya 70.0 m/s kwa angle ya 75.0º juu ya usawa, kama ilivyoonyeshwa kwenye Mchoro. Fyuzi ni wakati muafaka wa kuwaka shell kama inavyofikia kiwango chake cha juu juu juu ya ardhi.
- Tumia urefu ambao shell hupuka.
- Ni muda gani uliopita kati ya uzinduzi wa shell na mlipuko?
- Je! Uhamisho wa usawa wa shell unapopuka?
Mkakati
Kwa sababu upinzani wa hewa hauna maana kwa shell isiyopatikana, njia ya uchambuzi iliyoelezwa hapo juu inaweza kutumika. Mwendo unaweza kuvunjwa katika mwendo usio na usawa na wima ambao\(\displaystyle a_x=0\) na\(\displaystyle a_y=–g\). Tunaweza kisha kufafanua\(\displaystyle x_0\) na\(\displaystyle y_0\) kuwa sifuri na kutatua kwa kiasi taka.
Suluhisho kwa (a)
Kwa “urefu” tunamaanisha urefu au nafasi ya wima y juu ya hatua ya mwanzo. Sehemu ya juu katika trajectory yoyote, inayoitwa kilele, inafikiwa wakati\(\displaystyle v_y=0\). Kwa kuwa tunajua kasi ya awali na ya mwisho pamoja na nafasi ya awali, tunatumia equation ifuatayo ili kupata\(\displaystyle y\):
\(\displaystyle v^2_y=v^2_{0y}−2g(y−y_0)\).
Kwa sababu\(\displaystyle y_0\) na wote\(\displaystyle v_y\) ni sifuri, equation simplifies kwa
\(\displaystyle 0=v^2_{0y}−2gy.\)
Kutatua kwa\(\displaystyle y\) anatoa
\(\displaystyle y=\frac{v^2_{0y}}{2g}\).
Sasa tunapaswa kupata\(\displaystyle v_{0y}\), sehemu ya kasi ya awali katika y- mwelekeo. Inatolewa na\(\displaystyle v_{0y}=v_0sinθ\), wapi\(\displaystyle v_{0y}\) kasi ya awali ya 70.0 m/s, na\(\displaystyle θ_0=75.0º\) ni angle ya awali. Hivyo,
\(\displaystyle v_{0y}=v_0sinθ_0=(70.0 m/s)(sin 75º)=67.6 m/s.\)
na\(\displaystyle y\) ni
\(\displaystyle y=\frac{(67.6 m/s)^2}{2(9.80 m/s^2)}\),
ili
\(\displaystyle y=233m.\)
Majadiliano kwa (a)
Kumbuka kwamba kwa sababu up ni chanya, kasi ya awali ni chanya, kama urefu wa juu, lakini kasi kutokana na mvuto ni hasi. Kumbuka pia kwamba urefu wa juu unategemea tu sehemu ya wima ya kasi ya awali, ili projectile yoyote yenye sehemu ya wima ya awali ya 67.6 m/s kufikia urefu wa juu wa 233 m (kupuuza upinzani wa hewa). Nambari katika mfano huu ni busara kwa maonyesho makubwa ya moto, maganda ambayo yanafikia urefu huo kabla ya kulipuka. Katika mazoezi, upinzani wa hewa sio duni kabisa, na hivyo kasi ya awali ingekuwa kubwa zaidi kuliko ile iliyotolewa kufikia urefu sawa.
Suluhisho kwa (b)
Kama ilivyo katika matatizo mengi ya fizikia, kuna njia zaidi ya moja ya kutatua kwa muda hadi hatua ya juu. Katika kesi hii, njia rahisi ni kutumia\(\displaystyle y=y_0+\frac{1}{2}(v_{0y}+v_y)t\). Kwa sababu y0 ni sifuri, equation hii inapunguza tu
\(\displaystyle y=\frac{1}{2}(v_{0y}+v_y)t\).
Kumbuka kuwa kasi ya mwisho ya wima,\(\displaystyle v_y\), kwa kiwango cha juu ni sifuri. Hivyo,
\(\displaystyle t=\frac{2y}{(v_{0y}+v_y)}=\frac{2(233 m)}{(67.6 m/s)}=6.90 s.\)
Majadiliano kwa (b)
Wakati huu pia ni busara kwa fireworks kubwa. Unapoweza kuona uzinduzi wa fireworks, utaona sekunde kadhaa kupita kabla ya shell kulipuka. (Njia nyingine ya kutafuta muda ni kwa kutumia\(\displaystyle y=y_0+v_{0y}t−\frac{1}{2}gt^2\), na kutatua equation quadratic kwa\(\displaystyle t\).)
Suluhisho kwa (c)
Kwa sababu upinzani wa hewa ni mdogo,\(\displaystyle a_x=0\) na kasi ya usawa ni mara kwa mara, kama ilivyojadiliwa hapo juu. Uhamisho wa usawa ni kasi ya usawa inayoongezeka kwa wakati kama iliyotolewa na\(\displaystyle x=x_0+v_xt\), ambapo\(\displaystyle x_0\) ni sawa na sifuri:
\(\displaystyle x=v_xt,\)
\(\displaystyle v_x\)wapi x- sehemu ya kasi, ambayo hutolewa na\(\displaystyle v_x=v_0cosθ_0\). Sasa,
\(\displaystyle v_x=v_0cosθ_0=(70.0 m/s)(cos 75.0º)=18.1 m/s.\)
Wakati\(\displaystyle t\) wa mwendo wote ni sawa, na ndivyo\(\displaystyle x\) ilivyo
\(\displaystyle x=(18.1 m/s)(6.90 s)=125 m.\)
Majadiliano kwa (c)
Mwendo usio na usawa ni kasi ya mara kwa mara kwa kutokuwepo kwa upinzani wa hewa. Uhamisho usio na usawa unaopatikana hapa unaweza kuwa na manufaa katika kuweka vipande vya fireworks kutoka kuanguka kwa watazamaji. Mara baada ya shell kulipuka, upinzani wa hewa una athari kubwa, na vipande vingi vitashuka moja kwa moja chini.
Katika kutatua sehemu (a) ya mfano uliotangulia, maneno tuliyopata kwa y ni halali kwa mwendo wowote wa projectile ambapo upinzani wa hewa hauna maana. Piga urefu wa juu\(\displaystyle y=h\); basi,
\(\displaystyle h=\frac{v^2_{0y}}{2g}\).
Equation hii inafafanua urefu wa juu wa projectile na inategemea tu sehemu ya wima ya kasi ya awali.
KUFAFANUA MFUMO KURATIBU
Ni muhimu kuanzisha mfumo wa kuratibu wakati wa kuchunguza mwendo wa projectile. Sehemu moja ya kufafanua mfumo wa kuratibu ni kufafanua asili ya\(\displaystyle x\) na\(\displaystyle y\) nafasi. Mara nyingi, ni rahisi kuchagua nafasi ya awali ya kitu kama asili kama hiyo\(\displaystyle x_0=0\) na\(\displaystyle y_0=0\). Pia ni muhimu kufafanua maelekezo mazuri na mabaya katika maelekezo\(\displaystyle x\) na\(\displaystyle y\) maelekezo. Kwa kawaida, tunafafanua mwelekeo mzuri wa wima kama juu, na mwelekeo mzuri wa usawa ni kawaida mwelekeo wa mwendo wa kitu. Wakati hii ni kesi, kuongeza kasi ya wima\(\displaystyle g\), inachukua thamani hasi (kwa kuwa inaelekezwa chini kuelekea Dunia). Hata hivyo, mara kwa mara ni muhimu kufafanua kuratibu tofauti. Kwa mfano, kama wewe ni kuchambua mwendo wa mpira kutupwa chini kutoka juu ya mwamba, inaweza kuwa na maana ya kufafanua mwelekeo chanya chini tangu mwendo wa mpira ni tu katika mwelekeo wa chini. Ikiwa ndio kesi, g inachukua thamani nzuri.
Mfano\(\displaystyle \PageIndex{2}\): Calculating Projectile Motion: Hot Rock Projectile
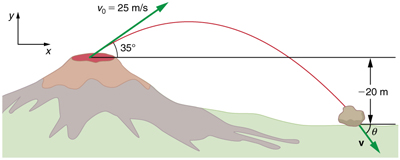
Kilauea katika Hawaii ni volkano duniani ya kuendelea kazi. Volkano yenye nguvu sana hutoa miamba nyekundu-moto na lava badala ya moshi na majivu. Tuseme mwamba mkubwa umeondolewa kutoka volkano kwa kasi ya 25.0 m/s na kwa pembe juu ya usawa, kama inavyoonekana kwenye Mchoro. Mwamba hupiga upande wa volkano kwenye urefu wa 20.0 m chini kuliko hatua yake ya kuanzia. (a) Kuhesabu muda unachukua mwamba kufuata njia hii. (b) Ukubwa na mwelekeo wa kasi ya mwamba katika athari ni nini?
Mkakati
Tena, kutatua mwendo huu mbili-dimensional katika harakati mbili za kujitegemea moja-dimensional itatuwezesha kutatua kwa kiasi kinachohitajika. Wakati projectile iko hewani inasimamiwa na mwendo wake wa wima pekee. Tutatatua kwa\(\displaystyle t\) kwanza. Wakati mwamba unapoongezeka na kuanguka kwa wima, mwendo wa usawa unaendelea kwa kasi ya mara kwa mara. Mfano huu unauliza kasi ya mwisho. Hivyo, matokeo ya wima na ya usawa yatarejeshwa ili kupata\(\displaystyle v\) na\(\displaystyle θ_v\) wakati wa mwisho kuamua katika sehemu ya kwanza ya mfano.
Suluhisho kwa (a)
Wakati mwamba uko hewani, huinuka na kisha huanguka kwenye nafasi ya mwisho 20.0 m chini kuliko urefu wake wa kuanzia. Tunaweza kupata muda kwa ajili ya hii kwa kutumia
\(\displaystyle y=y_0+v_{0y}t−\frac{1}{2}gt^2\).
Ikiwa tunachukua nafasi ya kwanza\(\displaystyle y_0\) kuwa sifuri, basi nafasi ya mwisho ni\(\displaystyle y=−20.0 m\). Sasa kasi ya wima ya awali ni sehemu ya wima ya kasi ya awali, iliyopatikana kutoka\(\displaystyle v_{0y}=v_0sinθ_0 = (25.0 m/s)(sin 35.0º) = 14.3 m/s.\) Kubadilisha maadili inayojulikana mavuno
\(\displaystyle −20.0 m=(14.3 m/s)t−(4.90 m/s^2)t^2\).
Kurekebisha maneno hutoa equation quadratic katika\(\displaystyle t\):
\(\displaystyle (4.90 m/s^2)t^2−(14.3 m/s)t−(20.0 m)=0.\)
Maneno haya ni equation ya quadratic ya fomu\(\displaystyle at^2+bt+c=0\), ambapo mara kwa mara ni\(\displaystyle a=4.90, b=–14.3\), na ufumbuzi\(\displaystyle c=–20.0.\) wake hutolewa na formula ya quadratic:
\(\displaystyle t=\frac{−b±\sqrt{b^2−4ac}}{2a}\).
Equation hii mavuno ufumbuzi mbili:\(\displaystyle t=3.96\) na\(\displaystyle t=–1.03\). (Imeachwa kama zoezi kwa msomaji kuthibitisha ufumbuzi huu.) Wakati ni\(\displaystyle t=3.96s\) au\(\displaystyle –1.03s\). Thamani mbaya ya wakati inamaanisha tukio kabla ya kuanza kwa mwendo, na hivyo tunaiondoa. Hivyo,
\(\displaystyle t=3.96 s.\)
Majadiliano kwa (a)
Wakati wa mwendo wa projectile umeamua kabisa na mwendo wa wima. Hivyo projectile yoyote ambayo ina kasi ya awali ya wima ya 14.3 m/s na ardhi 20.0 m chini ya urefu wake wa kuanzia itatumia 3.96 s katika hewa.
Suluhisho kwa (b)
Kutoka kwa habari sasa kwa mkono, tunaweza kupata kasi ya mwisho ya usawa\(\displaystyle v_x\) na wima\(\displaystyle v_y\) na kuchanganya yao ili kupata kasi ya jumla v na angle\(\displaystyle θ_0\) inafanya kwa usawa. Bila shaka,\(\displaystyle v_x\) ni mara kwa mara ili tuweze kutatua kwa ajili yake katika eneo lolote usawa. Katika kesi hii, tulichagua hatua ya mwanzo tangu tunajua kasi ya awali na angle ya awali. Kwa hiyo:
\(\displaystyle v_x=v_0cosθ_0=(25.0 m/s)(cos 35º)=20.5 m/s.\)
Kasi ya mwisho ya wima hutolewa na equation ifuatayo:
\(\displaystyle v_y=v_{0y}−gt\),
ambapo\(\displaystyle v_{0y}\) ilipatikana katika sehemu (a) kuwa 14.3 m/s. Hivyo,
\(\displaystyle v_y=14.3 m/s−(9.80 m/s^2)(3.96 s)\)
ili
\(\displaystyle v_y=−24.5 m/s.\)
Ili kupata ukubwa wa kasi ya mwisho v tunachanganya vipengele vyake vya perpendicular, kwa kutumia equation ifuatayo:
\(\displaystyle v=\sqrt{v^2_x+v^2_y}=\sqrt{(20.5 m/s)^2+(−24.5 m/s)^2}\),
ambayo inatoa
\(\displaystyle v=31.9 m/s.\)
Mwelekeo v hupatikana kutoka kwa equation:
\(\displaystyle θ_v=tan^{−1}(v_y/v_x)\)
ili
\(\displaystyle θ_v=tan^{−1}(−24.5/20.5)=tan^{−1}(−1.19).\)
Hivyo,
\(\displaystyle θ_v=−50.1º.\)
Majadiliano kwa (b)
Pembe hasi ina maana kwamba kasi ni 50.1º chini ya usawa. Matokeo haya ni sawa na ukweli kwamba mwisho wima kasi ni hasi na hivyo chini-kama ungependa kutarajia kwa sababu urefu wa mwisho ni 20.0 m chini kuliko urefu wa awali. (Angalia Kielelezo.)
Moja ya mambo muhimu zaidi yaliyoonyeshwa na mwendo wa projectile ni kwamba mwendo wa wima na usawa ni huru kwa kila mmoja. Galileo alikuwa mtu wa kwanza kuelewa kikamilifu tabia hii. Aliitumia kutabiri aina mbalimbali za projectile. Kwenye kiwango cha chini, tunafafanua mbalimbali kuwa umbali usio na usawa uliosafiri na projectile. Galileo na wengine wengi walivutiwa na aina mbalimbali za projectiles hasa kwa madhumuni ya kijeshi-kama vile kulenga mizinga. Hata hivyo, kuchunguza aina mbalimbali za projectiles kunaweza kutoa mwanga juu ya matukio mengine ya kuvutia, kama vile njia za satelaiti duniani kote. Hebu fikiria projectile mbalimbali zaidi.
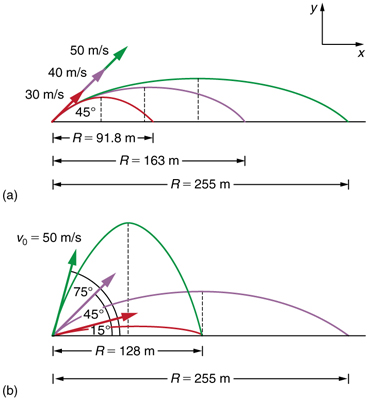
Je! Kasi ya awali ya projectile inaathirije aina yake? Kwa wazi, kasi kubwa ya awali\(\displaystyle v_0\), pana zaidi, kama inavyoonekana kwenye Mchoro (a). Pembe ya awali\(\displaystyle θ_0\) pia ina athari kubwa juu ya upeo, kama ilivyoonyeshwa kwenye Kielelezo (b). Kwa fasta kasi ya awali, kama vile inaweza kuwa zinazozalishwa na kanuni, mbalimbali upeo ni kupatikana kwa\(\displaystyle θ_0=45º\). Hii ni kweli tu kwa hali ya kupuuza upinzani wa hewa. Ikiwa upinzani wa hewa unazingatiwa, angle ya juu ni takriban\(\displaystyle 38º\). Kushangaza, kwa kila angle ya awali isipokuwa\(\displaystyle 45º\), kuna pembe mbili kwamba kutoa mbalimbali sawa-jumla ya pembe wale ni\(\displaystyle 90º\). Aina hiyo pia inategemea thamani ya kuongeza kasi ya mvuto\(\displaystyle g\). Mwanaanga wa mwezi Alan Shepherd aliweza kuendesha mpira wa golf umbali mkubwa juu ya Mwezi kwa sababu mvuto ni dhaifu huko. Aina mbalimbali\(\displaystyle R\) za projectile kwenye ardhi ya ngazi ambayo upinzani wa hewa ni duni hutolewa na
\(\displaystyle R=\frac{v^2_0sin2θ_0}{g}\),
wapi\(\displaystyle v_0\) kasi ya awali na\(\displaystyle θ_0\) ni angle ya awali kuhusiana na usawa. ushahidi wa equation hii ni wa kushoto kama tatizo mwisho sura (mwanga ni kutolewa), lakini haina fit sifa kuu ya projectile mbalimbali kama ilivyoelezwa.
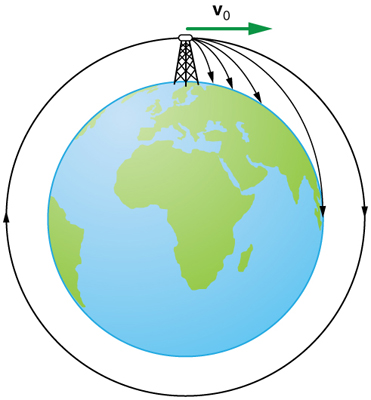
Tunaposema juu ya aina mbalimbali za projectile kwenye ardhi ya ngazi, tunadhani kuwa\(\displaystyle R\) ni ndogo sana ikilinganishwa na mzunguko wa Dunia. Kama, hata hivyo, mbalimbali ni kubwa, Dunia curves mbali chini ya projectile na kuongeza kasi ya mvuto mabadiliko mwelekeo njiani. Mbalimbali ni kubwa kuliko ilivyotabiriwa na equation mbalimbali iliyotolewa hapo juu kwa sababu projectile ina mbali zaidi kuanguka kuliko ingekuwa juu ya ardhi ya ngazi. (Angalia Kielelezo.) Ikiwa kasi ya awali ni ya kutosha, projectile inakwenda kwenye obiti. Hii inaitwa exit kasi. Uwezekano huu ulitambuliwa karne kabla ya kukamilika. Wakati kitu kiko katika obiti, Dunia inazunguka mbali na chini ya kitu kwa kiwango sawa na kinachoanguka. Kitu hivyo huanguka kwa kuendelea lakini kamwe hupiga uso. Mambo haya na mengine ya mwendo wa orbital, kama vile mzunguko wa Dunia, yatafunikwa kwa uchambuzi na kwa kina zaidi baadaye katika maandishi haya.
Mara nyingine tena tunaona kwamba kufikiri juu ya mada moja, kama vile upeo wa projectile, inaweza kutuongoza kwa wengine, kama vile mizunguko ya Dunia. Aidha ya Velocities, sisi kuchunguza nyongeza ya kasi, ambayo ni kipengele kingine muhimu ya kinematics mbili-dimensional na pia kutoa ufahamu zaidi ya mada ya haraka.
PHET EXPLORATIONS: PROJECTILE MWENDO
Mlipuko Buick nje ya kanuni! Jifunze kuhusu mwendo wa projectile kwa kurusha vitu mbalimbali. Weka angle, kasi ya awali, na wingi. Ongeza upinzani wa hewa. Kufanya mchezo nje ya simulation hii kwa kujaribu hit lengo.

Muhtasari
- Mwendo wa projectile ni mwendo wa kitu kupitia hewa ambayo ni chini ya kuongeza kasi ya mvuto tu.
- Ili kutatua matatizo ya mwendo wa projectile, fanya hatua zifuatazo:
- Kuamua mfumo wa kuratibu. Kisha, tatua msimamo na/au kasi ya kitu katika vipengele vya usawa na vya wima. Vipengele vya msimamo s vinatolewa kwa kiasi x na y, na vipengele vya kasi v vinatolewa na vx=vcosη na vy=vsin, ambapo v ni ukubwa wa kasi na η ni mwelekeo wake.
2. Kuchambua mwendo wa projectile katika mwelekeo usawa kwa kutumia equations zifuatazo:
\(\displaystyle \text{Horizontal motion}(a_x=0)\)
\(\displaystyle x=x_0+v_xt\)
\(\displaystyle v_x=v_{0x}=v_x=\text{velocity is a constant}\).
3. Kuchambua mwendo wa projectile katika mwelekeo wima kwa kutumia equations zifuatazo:
\(\displaystyle \text{Vertical motion(Assuming positive direction is up;}a_y=−g=−9.80 m/s^2)\)
\(\displaystyle y=y_0+\frac{1}{2}(v_{0y}+v_y)t\)
\(\displaystyle v_y=v_{0y}−gt\)
\(\displaystyle y=y_0+v_{0y}t−\frac{1}{2}gt^2\)
\(\displaystyle v^2_y=v^2_{0y}−2g(y−y_0)\).
4. Rejesha vipengele vya usawa na wima vya eneo na/au kasi kwa kutumia milinganyo ifuatayo:
\(\displaystyle s=\sqrt{x^2+y^2}\)
\(\displaystyle θ=tan^{−1}(y/x)\)
\(\displaystyle v=\sqrt{v^2_x+v^2_y}\)
\(\displaystyle θ_v=tan^{−1}(v_y/v_x)\).
- Urefu\(\displaystyle h\) wa juu wa projectile iliyozinduliwa na kasi ya awali ya wima\(\displaystyle v_{0y}\) hutolewa na
\(\displaystyle h=\frac{v^2_{0y}}{2g}\).
- Umbali wa juu wa usawa uliosafiri na projectile huitwa upeo. Aina mbalimbali\(\displaystyle R\) za projectile kwenye ardhi ya ngazi ilizinduliwa kwa pembe\(\displaystyle θ_0\) juu ya usawa na kasi\(\displaystyle v_0\) ya awali hutolewa na
\(\displaystyle R=\frac{v^2_0sin2θ_0}{g}\).
faharasa
- upinzani wa hewa
- nguvu ya msuguano ambayo hupunguza mwendo wa vitu wakati wa kusafiri kupitia hewa; wakati wa kutatua matatizo ya msingi ya fizikia, upinzani wa hewa unadhaniwa kuwa sifuri
- kinematiki
- utafiti wa mwendo bila kujali molekuli au nguvu
- mwendo
- uhamisho wa kitu kama kazi ya wakati
- ya kutupa
- kitu kwamba safari kwa njia ya hewa na uzoefu tu kuongeza kasi kutokana na mvuto
- mwendo wa kusokotoa
- mwendo wa kitu kwamba ni chini tu kwa kuongeza kasi ya mvuto
- anuwai
- umbali wa juu wa usawa ambao projectile husafiri
- mtupo wa angani
- njia ya projectile kupitia hewa


