2.3: Muda, kasi, na Kasi

Last updated
Save as PDF

Page ID: 183195

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Eleza uhusiano kati ya kasi ya papo hapo, kasi ya wastani, kasi ya haraka, kasi ya wastani, uhamisho, na wakati.
Tumia kasi na kasi iliyotolewa nafasi ya awali, wakati wa awali, nafasi ya mwisho, na wakati wa mwisho.
Kupata grafu ya kasi vs wakati kupewa grafu ya nafasi vs wakati.
Tafsiri grafu ya kasi vs wakati.

Kuna zaidi ya mwendo kuliko umbali na uhamisho. Maswali kama vile, “Mbio ya mguu inachukua muda gani?” na “Kasi ya mkimbiaji ilikuwa nini?” haiwezi kujibiwa bila ufahamu wa dhana nyingine. Katika sehemu hii tunaongeza ufafanuzi wa muda, kasi, na kasi ya kupanua maelezo yetu ya mwendo.

Konokono kuacha trails kinamasi kama wao mbio kila mmoja pamoja uso gorofa. — Kielelezo\(\PageIndex{1}\): Mwendo wa konokono hizi za racing zinaweza kuelezewa na kasi zao na kasi zao. (mikopo: tobitas flickr, Flickr)

Muda

Kama ilivyojadiliwa katika Kiasi cha Kimwili na Units, wingi wa kimsingi wa kimwili hufafanuliwa na jinsi wanavyopimwa. Hii ndio kesi kwa wakati. Kila kipimo cha muda kinahusisha kupima mabadiliko katika kiasi fulani cha kimwili. Inaweza kuwa namba kwenye saa ya digital, mapigo ya moyo, au nafasi ya Jua mbinguni. Katika fizikia, ufafanuzi wa muda ni rahisi— wakati ni mabadiliko, au muda juu ya mabadiliko ambayo hutokea. Haiwezekani kujua wakati huo umepita isipokuwa kitu kinabadilika.

Kiasi cha muda au mabadiliko ni sanifu kwa kulinganisha na kiwango. Kitengo cha SI kwa muda ni cha pili, kinachofupishwa s. tunaweza, kwa mfano, kuona kwamba pendulum fulani hufanya swing moja kamili kila 0.75 s Kisha tunaweza kutumia pendulum kupima muda kwa kuhesabu swings yake au, bila shaka, kwa kuunganisha pendulum kwa utaratibu wa saa ambayo inasajili wakati kwenye piga. Hii inaruhusu sisi si tu kupima kiasi cha muda, lakini pia kuamua mlolongo wa matukio.

Muda unahusianaje na mwendo? Kwa kawaida tunavutiwa na muda uliopita kwa mwendo fulani, kama vile inachukua muda gani abiria wa ndege kupata kutoka kiti chake hadi nyuma ya ndege. Ili kupata muda uliopita, tunaona wakati mwanzoni na mwisho wa mwendo na uondoe mbili. Kwa mfano, hotuba inaweza kuanza saa 11:00 A.M. na kumalizika saa 11:50 A.M., ili muda uliopita utakuwa dakika 50. Wakati uliopita\(Δt\) ni tofauti kati ya wakati wa kumalizia na wakati wa mwanzo,

\(Δt=t_f−t_0\),

wapi\(Δt\) mabadiliko katika wakati au wakati uliopita,\(t_f\) ni wakati mwishoni mwa mwendo, na\(t_0\) ni wakati mwanzoni mwa mwendo. (Kama kawaida, ishara ya delta\(Δ\), inamaanisha mabadiliko katika kiasi kinachofuata.)

Maisha ni rahisi kama wakati wa mwanzo\(t_0\) unachukuliwa kuwa sifuri, kama tunapotumia stopwatch. Ikiwa tulikuwa tunatumia stopwatch, ingekuwa tu kusoma sifuri mwanzoni mwa hotuba na dakika 50 mwishoni. Ikiwa\(t_0=0\), basi

\[Δt=t_f≡t.\]

Katika maandishi haya, kwa ajili ya unyenyekevu,

mwendo huanza wakati sawa na sifuri (\(t_0=0\))
ishara\(t\) ni kutumika kwa muda uliopita isipokuwa vinginevyo maalum (\(Δt=t_f≡t\))

Velocity

Dhana yako ya kasi pengine ni sawa na ufafanuzi wake wa kisayansi. Unajua kwamba kama una makazi yao kubwa katika kiasi kidogo cha muda una kasi kubwa, na kwamba kasi ina vitengo vya umbali kugawanywa na wakati, kama vile maili kwa saa au kilomita kwa saa.

Ufafanuzi: WASTANI WA kasi

Wastani kasi ni makazi yao (mabadiliko katika nafasi) kugawanywa na wakati wa kusafiri,

\[\bar{v}=\frac{Δx}{Δt}=\frac{x_f−x_0}{t_f−t_0}.\]

wapi\(\bar{v}\) wastani (unahitajika kwa bar juu ya\(v\)) kasi,\(Δx\) ni mabadiliko katika nafasi (au makazi yao),\(x_f\) na\(x_0\) ni nafasi ya mwisho na mwanzo wakati mwingine\(t_f\) na\(t_0\), kwa mtiririko huo. Ikiwa wakati wa kuanza\(t_0\) unachukuliwa kuwa sifuri, basi kasi ya wastani ni tu

\[\bar{v}=\frac{Δx}{t}.\]

Kumbuka kwamba ufafanuzi huu unaonyesha kwamba kasi ni vector kwa sababu makazi yao ni vector. Ina ukubwa wote na mwelekeo. Kitengo cha SI kwa kasi ni mita kwa sekunde au m/s, lakini vitengo vingine vingi, kama vile km/h, mi/h (pia imeandikwa kama mph), na cm/s, vinatumiwa kwa kawaida. Tuseme, kwa mfano, abiria wa ndege alichukua sekunde 5 kuhamia -4 m (ishara hasi inaonyesha kuwa uhamisho ni kuelekea nyuma ya ndege). Kasi yake wastani itakuwa

\[\bar{v}=\frac{Δx}{t}=\frac{−4\,m}{5\,s}=−0.8 \,m/s.\]

Ishara ndogo inaonyesha kasi ya wastani pia inaelekea nyuma ya ndege.

Kasi ya wastani ya kitu haituambii chochote kuhusu kinachotokea kati ya hatua ya mwanzo na hatua ya mwisho, hata hivyo. Kwa mfano, hatuwezi kujua kutoka kwa kasi ya wastani kama abiria wa ndege ataacha kwa muda mfupi au anarudi kabla hajaenda nyuma ya ndege. Ili kupata maelezo zaidi, ni lazima tuangalie makundi madogo ya safari kwa vipindi vidogo vya muda mfupi.

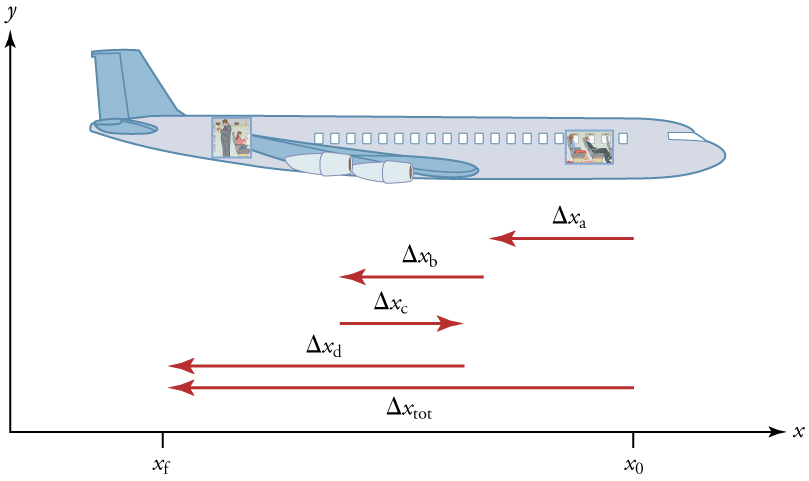
Ndege inavyoonekana kutoka nje. Mishale ya vector inaonyesha njia za kila sehemu ya mtu binafsi ya safari ya abiria nyuma ya ndege. — Kielelezo\(\PageIndex{2}\): rekodi ya kina zaidi ya abiria ndege kuelekea nyuma ya ndege, kuonyesha makundi madogo ya safari yake.

Vipindi vidogo vya muda vinavyozingatiwa katika mwendo, maelezo zaidi. Tunapobeba mchakato huu kwa hitimisho lake la mantiki, tunasalia na muda mdogo mdogo. Zaidi ya muda huo, kasi ya wastani inakuwa kasi ya papo hapo au kasi kwa papo fulani. Speedometer ya gari, kwa mfano, inaonyesha ukubwa (lakini sio mwelekeo) wa kasi ya haraka ya gari. (Polisi hutoa tiketi kulingana na kasi ya haraka, lakini wakati wa kuhesabu muda gani utachukua kupata kutoka sehemu moja hadi nyingine kwenye safari ya barabara, unahitaji kutumia kasi ya wastani.) Kasi ya haraka\(v\) ni kasi ya wastani kwa papo maalum kwa wakati (au juu ya muda mdogo wa muda mfupi).

Kihisabati, kutafuta kasi instantaneous\(v\),, kwa papo sahihi\(t\) inaweza kuhusisha kuchukua kikomo, operesheni calculus zaidi ya upeo wa maandishi haya. Hata hivyo, chini ya hali nyingi, tunaweza kupata maadili sahihi kwa kasi ya papo hapo bila calculus.

Kasi

Katika lugha ya kila siku, watu wengi hutumia maneno “kasi” na “kasi” kwa kubadilishana. Katika fizikia, hata hivyo, hawana maana sawa na ni dhana tofauti. Tofauti moja kubwa ni kwamba kasi haina mwelekeo. Hivyo kasi ni scalar. Kama vile tunahitaji kutofautisha kati ya kasi ya haraka na kasi ya wastani, tunahitaji pia kutofautisha kati ya kasi ya haraka na kasi ya wastani.

Kasi ya haraka ni ukubwa wa kasi ya papo hapo. Kwa mfano, tuseme abiria wa ndege kwa papo moja alikuwa na kasi ya instantaneous ya -3.0 m/s (maana ya chini kuelekea nyuma ya ndege). Wakati huo huo kasi yake instantaneous ilikuwa 3.0 m/s Au tuseme kwamba wakati mmoja wakati wa safari ya ununuzi kasi yako instantaneous ni 40 km/h kutokana kaskazini. Kasi yako instantaneous katika papo kwamba itakuwa 40 km/h-ukubwa sawa lakini bila mwelekeo. Wastani wa kasi, hata hivyo, ni tofauti sana na kasi ya wastani. Wastani wa kasi ni umbali uliosafiri umegawanyika na muda uliopita.

Tumebainisha kuwa umbali uliosafiri unaweza kuwa mkubwa zaidi kuliko uhamisho. Hivyo kasi ya wastani inaweza kuwa kubwa kuliko kasi ya wastani, ambayo ni makazi yao kugawanywa na wakati. Kwa mfano, kama wewe gari kwa duka na kurudi nyumbani katika nusu saa, na odometer gari yako inaonyesha umbali jumla alisafiri ilikuwa 6 km, basi kasi yako wastani ilikuwa 12 km/h. kasi yako wastani, hata hivyo, ilikuwa sifuri, kwa sababu makazi yako kwa ajili ya safari ya pande zote ni sifuri. (Uhamisho ni mabadiliko katika nafasi na, hivyo, ni sifuri kwa safari ya pande zote.) Hivyo kasi ya wastani sio tu ukubwa wa kasi ya wastani.

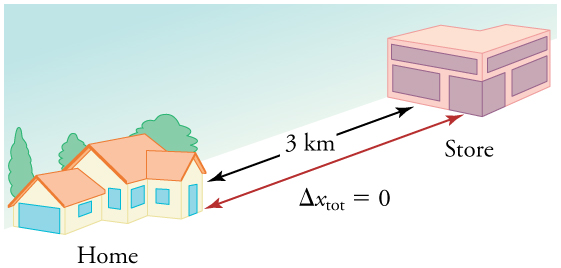
Nyumba na duka, na seti ya mishale kati ya kuonyesha kwamba umbali kati yao ni 3 kumweka 0 kilomita na umbali jumla alisafiri, delta x jumla, sawa 0 kilomita. — Kielelezo\(\PageIndex{3}\): Wakati wa safari ya dakika 30 kwenye duka, umbali wa jumla uliosafiri ni kilomita 6. Kasi ya wastani ni 12 km/h. makazi yao kwa ajili ya safari ya pande zote ni sifuri, kwa kuwa hakuna mabadiliko halisi katika nafasi. Hivyo kasi ya wastani ni sifuri.

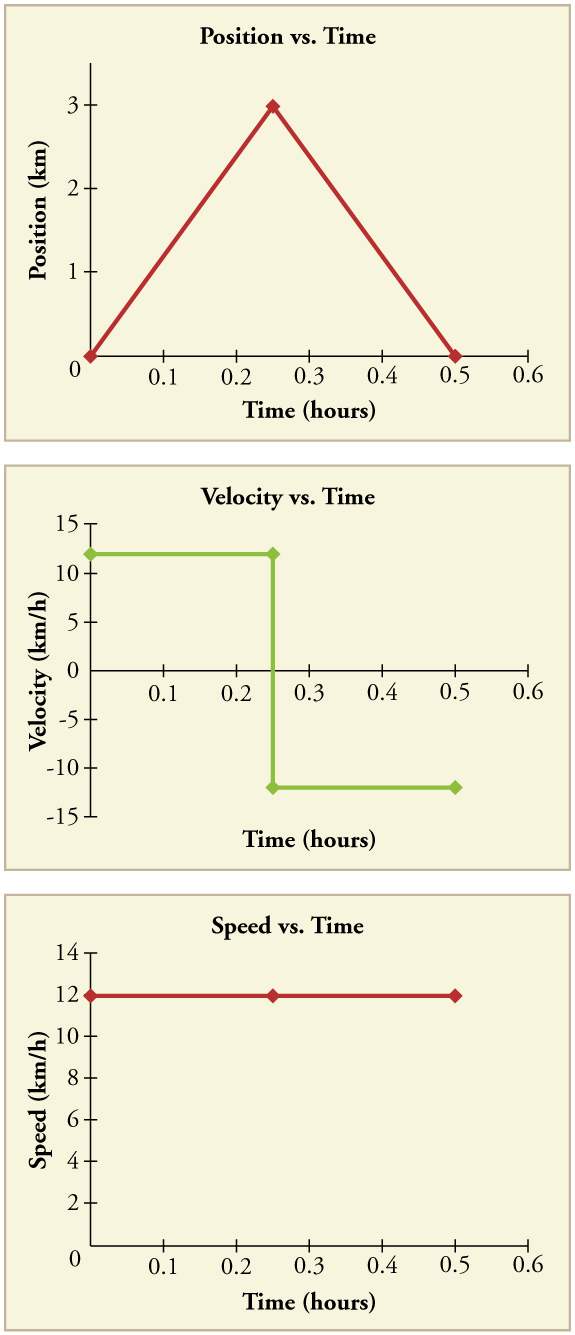
Njia nyingine ya kutazama mwendo wa kitu ni kutumia grafu. Mpango wa nafasi au kasi kama kazi ya muda inaweza kuwa muhimu sana. Kwa mfano, kwa safari hii ya duka, nafasi, kasi, na kasi-vs. grafu za wakati zinaonyeshwa kwenye Kielelezo\(\PageIndex{4}\). (Kumbuka kwamba grafu hizi zinaonyesha mfano rahisi sana wa safari. Sisi ni kudhani kwamba kasi ni mara kwa mara wakati wa safari, ambayo ni unrealistic kutokana na kwamba tutaweza pengine kuacha katika duka. Lakini kwa ajili ya unyenyekevu, tutaifanya mfano bila kuacha au mabadiliko kwa kasi. Pia tunadhani kwamba njia kati ya duka na nyumba ni mstari wa moja kwa moja kabisa.)

Grafu tatu za mstari. Kwanza line grafu ni ya nafasi katika kilomita dhidi ya muda katika masaa. Mstari huongezeka kwa mstari kutoka kilomita 0 hadi kilomita 6 katika hatua ya kwanza ya 0 masaa 25. Halafu hupungua kwa mstari kutoka kilomita 6 hadi kilomita 0 kati ya 0 kumweka 25 na 0 kumweka masaa 5. Mstari wa pili grafu inaonyesha kasi katika kilomita kwa saa dhidi ya muda katika masaa. Mstari ni gorofa saa kilomita 12 kwa saa kutoka wakati 0 hadi wakati 0 uhakika 25. Ni wima wakati wa 0 uhakika wa 25, kuacha kutoka kilomita 12 kwa saa hadi kilomita 12 hasi kwa saa. Ni gorofa tena katika hasi 12 kilomita kwa saa kutoka 0 uhakika 25 masaa 0 uhakika 5 masaa. Tatu line grafu inaonyesha kasi katika kilomita kwa saa dhidi ya muda katika masaa. Mstari ni gorofa kwa kilomita 12 kwa saa kutoka wakati sawa na 0 hadi wakati sawa na 0 kumweka masaa 5. — Kielelezo\(\PageIndex{4}\): Nafasi vs wakati, kasi vs wakati, na kasi vs. wakati katika safari. Kumbuka kuwa kasi ya safari ya kurudi ni hasi.

KUFANYA UHUSIANO: KUCHUKUA-NYUMBANI UCHUNGUZI - KUPATA HISIA YA KASI

Ikiwa umetumia muda mwingi kuendesha gari, labda una hisia nzuri ya kasi kati ya maili 10 na 70 kwa saa. Lakini ni nini katika mita kwa pili? Tuna maana gani tunaposema kuwa kitu kinachohamia saa 10 m/s? Ili kupata hisia bora ya nini maadili haya yanamaanisha kweli, fanya uchunguzi na mahesabu peke yako:

tumia kasi ya gari ya kawaida kwa mita kwa pili
makadirio ya kutembea na kutembea kasi kwa muda mwenyewe; kubadilisha vipimo katika wote m/s na mi/h
kuamua kasi ya ant, konokono, au jani la kuanguka

Zoezi\(\PageIndex{1}\)

Treni ya abiria inasafiri kutoka Baltimore hadi Washington, DC, na kurudi katika saa 1 na dakika 45. Umbali kati ya vituo hivyo viwili ni takriban maili 40. Ni nini

kasi ya wastani ya treni, na
kasi ya treni katika m/s?

Jibu

(a) Kasi ya wastani ya treni ni sifuri kwa sababu\(x_f=x_0\); treni inaishia mahali pale inapoanza.

(b) Kasi ya wastani ya treni imehesabiwa chini. Kumbuka kuwa treni husafiri maili 40 kwa njia moja na maili 40 nyuma, kwa umbali wa jumla wa maili 80.

\(\frac{distance}{time}=\frac{80 miles}{105 minutes}\)

\(\frac{80 miles}{105 minutes}×\frac{5280 feet}{1 mile}×\frac{1 meter}{3.28 feet}×\frac{1 minute}{60 seconds}=20 m/s\)

Muhtasari

Muda hupimwa kwa suala la mabadiliko, na kitengo chake cha SI ni cha pili (s). Ilipita muda kwa ajili ya tukio\(t_f\) ni\[Δt=t_f−t_0 \nonumber,\] wapi wakati wa mwisho na\(t_0\) ni mara ya awali. Wakati wa awali mara nyingi huchukuliwa kuwa sifuri, kama kupimwa na stopwatch; muda uliopita ni basi tu\(t\).
Wastani kasi\(\bar{v}\) hufafanuliwa kama makazi yao kugawanywa na wakati wa kusafiri. Katika alama, kasi ya wastani ni\[\bar{v}=\frac{Δx}{Δt}=\frac{x_f−x_0}{t_f−t_0} \nonumber.\]
Kitengo cha SI cha kasi ni m/s.
Velocity ni vector na hivyo ina mwelekeo.
Kasi ya papo hapo\(v\) ni kasi kwa papo maalum au kasi ya wastani kwa muda usio na kipimo.
Kasi ya haraka ni ukubwa wa kasi ya papo hapo.
Kasi ya haraka ni kiasi cha scalar, kwa kuwa haina mwelekeo maalum.
Wastani wa kasi ni umbali wa jumla uliosafiri umegawanyika na muda uliopita. (Wastani wa kasi sio ukubwa wa kasi ya wastani.) Kasi ni kiasi cha scalar; haina mwelekeo unaohusishwa nayo.

faharasa

kasi ya wastani: umbali alisafiri kugawanywa na wakati ambapo mwendo hutokea

kasi ya wastani: uhamisho umegawanyika na wakati juu ya uhamisho ambao hutokea

kasi ya papo hapo: kasi kwa papo maalum, au kasi ya wastani juu ya muda infinitesimal wakati

kasi ya papo hapo: ukubwa wa kasi ya papo hapo

wakati: mabadiliko, au muda juu ya mabadiliko ambayo hutokea

mfano: maelezo rahisi ambayo ina mambo hayo tu muhimu kuelezea fizikia ya hali ya kimwili

muda uliopita: tofauti kati ya wakati wa kumalizia na wakati wa mwanzo