16.2: Mstari wa Mstari

Malengo ya kujifunza

• Tumia mstari wa scalar muhimu pamoja na pembe.
• Tumia mstari wa vector muhimu pamoja na Curve iliyoelekezwa katika nafasi.
• Matumizi line muhimu kukokotoa kazi kufanyika katika kusonga kitu pamoja Curve katika uwanja vector.
• Eleza mzunguko na mzunguko wa shamba la vector.

Tunajua na integrals moja-variable ya fomu\(\displaystyle \int_{a}^{b}f(x)\,dx\), ambapo uwanja wa ushirikiano ni muda\([a,b]\). Muda huo unaweza kufikiriwa kama safu katika\(xy\) -ndege, tangu muda unafafanua sehemu ya mstari na mwisho\((a,0)\) na\((b,0)\) - kwa maneno mengine, sehemu ya mstari iko kwenye\(x\) -axis. Tuseme tunataka kuunganisha juu ya Curve yoyote katika ndege, si tu juu ya sehemu line juu ya\(x\) -axis. Kazi hiyo inahitaji aina mpya ya muhimu, inayoitwa mstari muhimu.

Line integrals na maombi mengi ya uhandisi na fizikia. Pia hutuwezesha kufanya generalizations kadhaa muhimu ya Theorem ya Msingi ya Calculus. na, wao ni karibu kushikamana na mali ya mashamba vector, kama tutaona.

Scalar line Integrals

Muhimu wa mstari unatupa uwezo wa kuunganisha kazi nyingi na mashamba ya vector juu ya curves ya kiholela katika ndege au katika nafasi. Kuna aina mbili za integrals line: scalar line integrals na vector line integrals. Scalar line integrals ni integrals ya kazi scalar juu ya Curve katika ndege au katika nafasi. Vector line integrals ni integrals ya uwanja vector juu Curve katika ndege au katika nafasi. Hebu tuangalie integrals mstari wa scalar kwanza.

line scalar muhimu hufafanuliwa kama muhimu single-variable inavyoelezwa, isipokuwa kwamba kwa mstari scalar muhimu, integrand ni kazi ya variable zaidi ya moja na uwanja wa ushirikiano ni Curve katika ndege au katika nafasi, kinyume na Curve juu ya\(x\) -axis.

Kwa scalar line muhimu, sisi basi\(C\) kuwa Curve laini katika ndege au katika nafasi na basi ff kuwa kazi na uwanja kuwa ni pamoja na\(C\). Sisi kukata curve katika vipande vidogo. Kwa kila kipande, sisi kuchagua uhakika\(P\) katika kipande kwamba na kutathmini\(f\) katika\(P\). (Tunaweza kufanya hivyo kwa sababu pointi zote katika Curve ni katika uwanja wa\(f\).) Tunazidisha\(f(P)\) kwa urefu wa arc wa kipande\(\Delta s\), kuongeza bidhaa\(f(P)\Delta s\) juu ya vipande vyote, na kisha basi urefu wa arc wa vipande hupungua hadi sifuri kwa kuchukua kikomo. Matokeo yake ni mstari wa scalar muhimu wa kazi juu ya pembe.

Kwa maelezo rasmi ya mstari scalar muhimu, basi\(C\) kuwa Curve laini katika nafasi iliyotolewa na parameterization\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). Hebu\(f(x,y,z)\) kuwa kazi na uwanja kuwa ni pamoja na Curve\(C\). Ili kufafanua mstari muhimu wa kazi\(f\) juu\(C\), tunaanza kama ufafanuzi zaidi wa kuanza muhimu: sisi kukata curve katika vipande vidogo. Kugawanya muda wa parameter\([a,b]\) katika\(n\) sehemu ndogo\([t_{i−l},t_i]\) za upana sawa\(1≤i≤n\), wapi\(t_0=a\) na\(t_n=b\) (Kielelezo\(\PageIndex{1}\)). Hebu\(t_{i}^*\) kuwa thamani katika\(i^{th}\) kipindi\([t_{i−l},t_i]\). Eleza mwisho wa\(\vecs r(t_0)\),\(\vecs r(t_1)\),...,\(\vecs r(t_n)\) na\(P_0\),...,\(P_n\). Pointi P _i kugawanya curve\(C\)\(n\) vipande vipande\(C_1\)\(C_2\),,...\(C_n\),, na urefu\(\Delta s_1\),\(\Delta s_2\),...,\(\Delta s_n\), kwa mtiririko huo. Hebu\(P_{i}^*\) kuashiria mwisho wa\(\vecs r(t_{i}^*)\) kwa\(1≤i≤n\). Sasa, sisi kutathmini kazi\(f\) katika hatua\(P_{i}^*\) kwa\(1≤i≤n\). Kumbuka kwamba\(P_{i}^*\) ni katika kipande\(C_1\), na kwa hiyo\(P_{i}^*\) ni katika uwanja wa\(f\). Kuzidisha\(f(P_{i}^*)\) kwa urefu\(\Delta s_1\) wa\(C_1\), ambayo inatoa eneo la “karatasi” na msingi\(C_1\), na urefu\(f(P_{i}^{*})\). Hii ni sawa na kutumia rectangles kwa eneo takriban katika moja ya kutofautiana muhimu. Sasa, tunaunda jumla\(\displaystyle \sum_{i=1}^{n} f(P_{i}^{*})\,\Delta s_i\).

Kielelezo\(\PageIndex{1}\): Curve\(C\) imegawanywa katika vipande n, na hatua ndani ya kila kipande amechaguliwa.

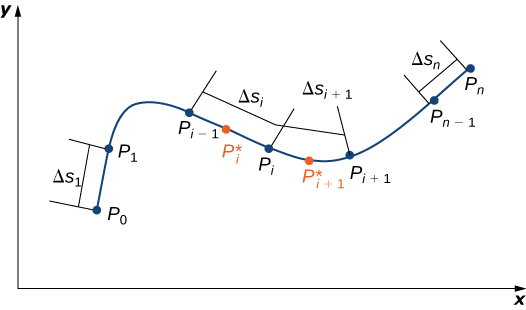
Kumbuka kufanana kwa jumla hii dhidi Riemann jumla; kwa kweli, ufafanuzi huu ni generalization ya jumla Riemann kwa curves holela katika nafasi. Kama vile kwa kiasi Riemann na integrals ya fomu\(\displaystyle \int_{a}^{b}g(x)\,dx\), sisi kufafanua muhimu kwa kuruhusu upana wa vipande vya Curve shrink kwa sifuri kwa kuchukua kikomo. Matokeo yake ni mstari wa scalar muhimu wa\(f\) pamoja\(C\).

Huenda umeona tofauti kati ya ufafanuzi huu wa mstari wa scalar muhimu na moja-variable muhimu. Katika ufafanuzi huu, urefu wa arc\(\Delta s_1\)\(\Delta s_2\),,...,\(\Delta s_n\) si lazima sawa; katika ufafanuzi wa moja-variable muhimu, Curve\(x\) katika-axis ni partitioned katika vipande vya urefu sawa. Tofauti hii haina athari yoyote katika kikomo. Tunapopunguza urefu wa arc hadi sifuri, maadili yao yanakaribia kutosha kwamba tofauti yoyote ndogo inakuwa haina maana.

Ufafanuzi: Scalar Line Integral

Hebu\(f\) kuwa kazi na uwanja kuwa ni pamoja na Curve laini\(C\) kwamba ni parameterized na\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). Mstari wa scalar muhimu wa\(f\) pamoja\(C\) ni

\[\int_C f(x,y,z) \,ds=\lim_{n\to\infty}\sum_{i=1}^{n}f(P_{i}^{*})\,\Delta s_i \label{eq12a} \]

kama kikomo hiki ipo (\(t_i ^{*}\)na\(\Delta s_i\) hufafanuliwa kama katika aya zilizopita). Ikiwa\(C\) ni safu ya mipango, basi\(C\) inaweza kuwakilishwa na equations parametric\(x=x(t)\),\(y=y(t)\), na\(a≤t≤b\). Ikiwa\(C\) ni laini na\(f(x,y)\) ni kazi ya vigezo viwili, basi mstari wa scalar muhimu wa\(f\) pamoja\(C\) hufafanuliwa sawa na

\[\int_C f(x,y) \,ds=\lim_{n\to\infty}\sum_{i=1}^{n} f(P_{i}^{*})\,\Delta s_i, \label{eq13} \]

kama kikomo hii ipo.

Ikiwa\(f\) ni kazi inayoendelea kwenye safu ya laini\(C\), basi\(\displaystyle \int_C f \,ds\) daima ipo. Tangu\(\displaystyle \int_C f \,ds\) hufafanuliwa kama kikomo cha Riemann kiasi, mwendelezo wa\(f\) ni wa kutosha ili kuhakikisha kuwepo kwa kikomo, kama muhimu\(\displaystyle \int_{a}^{b}g(x)\,dx\) ipo kama\(g\) ni kuendelea juu ya\([a,b]\).

Kabla ya kuangalia jinsi ya kukokotoa mstari muhimu, tunahitaji kuchunguza jiometri iliyochukuliwa na integrals hizi. Tuseme kwamba\(f(x,y)≥0\) kwa pointi zote\((x,y)\) kwenye curve laini planar\(C\). Fikiria kuchukua Curve\(C\) na projecting ni “juu” kwa uso inavyoelezwa na\(f(x,y)\), na hivyo kujenga Curve mpya\(C′\) ambayo iko katika grafu ya\(f(x,y)\) (Kielelezo\(\PageIndex{2}\)). Sasa tunaacha “karatasi” kutoka\(C′\) chini hadi\(xy\) ndege. Eneo la karatasi hii ni\(\displaystyle \int_C f(x,y)ds\). Ikiwa\(f(x,y)≤0\) kwa pointi fulani\(C\), basi thamani ya\(\displaystyle \int_C f(x,y)\,ds\) ni eneo la juu\(xy\) -ndege chini ya eneo chini ya\(xy\) -ndege. (Kumbuka kufanana na integrals ya fomu\(\displaystyle \int_{a}^{b}g(x)\,dx\).)

Kielelezo\(\PageIndex{2}\): Eneo la karatasi ya bluu ni\(\displaystyle \int_C f(x,y)\,ds\).

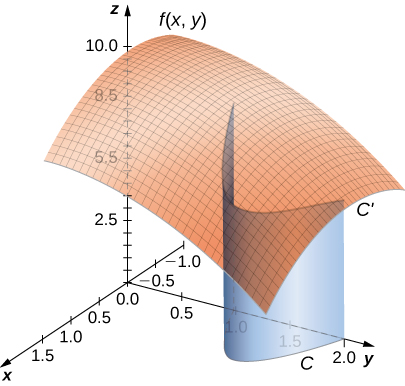
Kutoka jiometri hii, tunaweza kuona kwamba mstari muhimu\(\displaystyle \int_C f(x,y)\,ds\) hautegemei parameterization\(\vecs r(t)\) ya\(C\). Kwa muda mrefu kama curve inapita mara moja na parameterization, eneo la karatasi lililoundwa na kazi na curve ni sawa. Aina hii ya hoja ya kijiometri inaweza kupanuliwa ili kuonyesha kwamba mstari muhimu wa kazi tatu-variable juu ya Curve katika nafasi hautegemei parameterization ya Curve.

Mfano\(\PageIndex{1}\): ​​​​​​Finding the Value of a Line Integral

Pata thamani ya muhimu\(\displaystyle \int_C 2\,ds\), wapi nusu\(C\) ya juu ya mduara wa kitengo.

Suluhisho

Jumuiya ni\(f(x,y)=2\). Kielelezo\(\PageIndex{3}\) inaonyesha grafu ya\(f(x,y)=2\), Curve C, na karatasi sumu na wao. Angalia kwamba karatasi hii ina eneo sawa na mstatili na upana\(\pi\) na urefu\(2\). Kwa hiyo,\(\displaystyle \int_C 2 \,ds=2\pi\,\text{units}^2\).

Kielelezo\(\PageIndex{3}\): Karatasi ambayo hutengenezwa na nusu ya juu ya mduara wa kitengo katika ndege na grafu ya\(f(x,y)=2\).

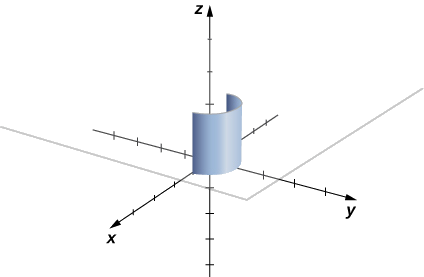
Kuona kwamba\(\displaystyle \int_C 2 \,ds=2\pi\) kwa kutumia ufafanuzi wa mstari muhimu, sisi basi\(\vecs r(t)\) kuwa parameterization ya\(C\). Kisha,\(f(\vecs r(t_i))=2\) kwa idadi yoyote\(t_i\) katika uwanja wa\(\vecs r\). Kwa hiyo,

\[\begin{align*} \int_C f \,ds &=\lim_{n\to\infty}\sum_{i=1}^{n} f(\vecs r(t_{i}^{*}))\,\Delta s_i \\[4pt] &=\lim_{n\to\infty}\sum_{i=1}^{n}2\,\Delta s_i \\[4pt] &=2\lim_{n\to\infty}\sum_{i=1}^{n}\,\Delta s_i \\[4pt] &=2(\text{length}\space \text{of}\space C) \\[4pt] &=2\pi \,\text{units}^2. \end{align*}\]

Zoezi\(\PageIndex{1}\)

Kupata thamani ya\(\displaystyle \int_C(x+y)\,ds\), ambapo\(C\) ni Curve parameterized na\(x=t\),\(y=t\),\(0≤t≤1\).

Kidokezo

Kupata sura sumu\(C\) na grafu ya kazi\(f(x,y)=x+y\).

Jibu

\(\sqrt{2}\)

Kumbuka kuwa katika mstari wa scalar muhimu, ushirikiano unafanywa kwa heshima na urefu wa arc\(s\), ambayo inaweza kufanya mstari wa scalar vigumu kuhesabu. Kufanya mahesabu rahisi, tunaweza kutafsiri\(\displaystyle \int_C f\,ds\) kwa muhimu na kutofautiana ya ushirikiano yaani\(t\).

Hebu\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\) kwa\(a≤t≤b\) kuwa parameterization ya\(C\). Kwa kuwa sisi ni kuchukua kwamba\(C\) ni laini,\(\vecs r′(t)=⟨x′(t),y′(t),z′(t)⟩\) ni kuendelea kwa wote\(t\) katika\([a,b]\). Hasa,,\(x′(t)\)\(y′(t)\), na\(z′(t)\) kuwepo kwa wote\(t\) katika\([a,b]\). Kwa mujibu wa formula ya urefu wa arc, tuna

\[\text{length}(C_i)=\Delta s_i=\int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt. \nonumber \]

Ikiwa upana\(\Delta t_i=t_i−t_{i−1}\) ni mdogo, basi kazi\(\displaystyle \int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt\,≈\,‖\vecs r′(t_i^*)‖\,\Delta t_i\),\(‖\vecs r′(t)‖\) ni karibu mara kwa mara juu ya muda\([t_{i−1},t_i]\) .Kwa hiyo,

\[\int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt\,≈\,‖\vecs r′(t_{i}^{*})‖\,\Delta t_i, \label{approxLineIntEq1} \]

na tuna

\[\sum_{i=1}^{n} f(\vecs r(t_i^*))\,\Delta s_i\approx\sum_{i=1}^{n} f(\vecs r(t_{i}^{*})) ‖\vecs r′(t_{i}^{*})‖\,\Delta t_i. \nonumber \]

Angalia Kielelezo\(\PageIndex{4}\).

Kielelezo\(\PageIndex{4}\): Kama sisi kuvuta juu ya Curve kutosha kwa kufanya ndogo\(\Delta t_i\) sana, basi kipande sambamba ya Curve ni takriban linear.

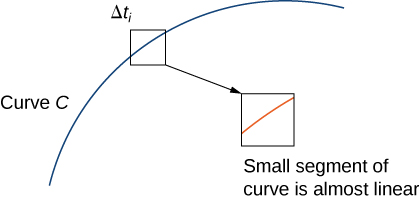
Kumbuka kwamba

\[\lim_{n\to\infty}\sum_{i=1}^{n} f(\vecs r(t_i^*))‖\vecs r′(t_{i}^{*})‖\,\Delta t_i=\int_a^b f(\vecs r(t))‖\vecs r′(t)‖\,dt. \nonumber \]

Kwa maneno mengine, kama upana wa vipindi\([t_{i−1},t_i]\) hupungua hadi sifuri, jumla\(\displaystyle \sum_{i=1}^{n} f(\vecs r(t_i^{*}))‖\vecs r′(t_{i}^{*})‖\,\Delta t_i\) hujiunga na muhimu\(\displaystyle \int_{a}^{b}f(\vecs r(t))‖\vecs r′(t)‖\,dt\). Kwa hiyo, tuna theorem ifuatayo.

Theorem: Kutathmini Mstari wa Scalar Integral

Hebu\(f\) kuwa kazi inayoendelea na uwanja unaojumuisha safu ya laini\(C\) na parameterization\(\vecs r(t)\),\(a≤t≤b\). Kisha

\[\int_C f \,ds=\int_{a}^{b} f(\vecs r(t))‖\vecs r′(t)‖\,dt.\label{scalerLineInt1} \]

Ingawa tuna kinachoitwa Equation\ ref {AproxLineIntEQ1} kama equation, ni usahihi zaidi kuchukuliwa makadirio kwa sababu tunaweza kuonyesha kwamba upande wa kushoto wa Equation\ ref {AproxLineIntEQ1} mbinu upande wa kulia kama\(n\to\infty\). Kwa maneno mengine, kuruhusu upana wa vipande kupungua hadi sifuri hufanya jumla ya mkono wa kulia karibu na jumla ya mkono wa kushoto. Tangu

\[‖\vecs r′(t)‖=\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2}, \nonumber \]

sisi kupata theorem zifuatazo, ambayo sisi kutumia kukokotoa scalar line integrals.

Theorem: Scalar Line Integral Hesabu

Hebu\(f\) kuwa kazi inayoendelea na uwanja unaojumuisha safu ya laini\(C\) na parameterization\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). Kisha

\[\int_C f(x,y,z) \,ds=\int_{a}^{b} f(\vecs r(t))\sqrt{({x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} \,dt. \nonumber \]

Vile vile,

\[\int_C f(x,y) \,ds=\int_{a}^{b}f(\vecs r(t))\sqrt{{(x′(t))}^2+{(y′(t))}^2} \,dt \nonumber \]

ikiwa\(C\) ni Curve planar na\(f\) ni kazi ya vigezo viwili.

Kumbuka kuwa matokeo ya theorem hii ni equation\(ds=‖\vecs r′(t)‖ \,dt\). Kwa maneno mengine, mabadiliko katika urefu wa arc yanaweza kutazamwa kama mabadiliko\(t\) katika-domain, yaliyowekwa na ukubwa wa vector\(\vecs r′(t)\).

Mfano\(\PageIndex{2}\): Evaluating a Line Integral

Kupata thamani ya muhimu\(\displaystyle \int_C(x^2+y^2+z) \,ds\), ambapo\(C\) ni sehemu ya helix parameterized na\(\vecs r(t)=⟨\cos t,\sin t,t⟩\),\(0≤t≤2\pi\).

Suluhisho

Kukokotoa scalar line muhimu, sisi kuanza kwa kuwabadili variable ya ushirikiano kutoka urefu safu\(s\) kwa\(t\). Kisha, tunaweza kutumia Equation\ ref {eq12a} kukokotoa muhimu kwa heshima na\(t\). Kumbuka kwamba

\[f(\vecs r(t))={\cos}^2 t+{\sin}^2 t+t=1+t \nonumber \]

na

\[\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} =\sqrt{{(−\sin(t))}^2+{\cos}^2(t)+1} =\sqrt{2}.\nonumber \]

Kwa hiyo,

\[\int_C(x^2+y^2+z) \,ds=\int_{0}^{2\pi} (1+t)\sqrt{2} \,dt. \nonumber \]

Kumbuka kwamba Equation\ ref {eq12a} kutafsiriwa awali ngumu line muhimu katika kusimamiwa moja-variable muhimu. Tangu

\ [kuanza {align*}\ int_ {0} ^ {2\ pi} (1+t)\ sqrt {2}\, dt &= {\ kushoto [\ sqrt {2} t+\ dfrac {\ sqrt {2} t^2} {2}\ haki]} _ {0} ^ {2\ pi}\ [4pt]
&=2\ sqrt 2 {}\ pi+2\ sqrt {2} {\ pi} ^2,\ mwisho {align*}\]

tuna

\[\int_C(x^2+y^2+z) \,ds=2\sqrt{2}\pi+2\sqrt{2}{\pi}^2. \nonumber \]

Zoezi\(\PageIndex{2}\)

Tathmini\(\displaystyle \int_C(x^2+y^2+z)ds\), ambapo C ni safu na parameterization\(\vecs r(t)=⟨\sin(3t),\cos(3t)⟩\),\(0≤t≤\dfrac{\pi}{4}\).

Kidokezo

Tumia toleo la kutofautiana la ufafanuzi muhimu wa mstari wa scalar (Equation\ ref {eq13}).

Jibu

\[\dfrac{1}{3}+\dfrac{\sqrt{2}}{6}+\dfrac{3\pi}{4} \nonumber \]

Mfano\(\PageIndex{3}\): Independence of Parameterization

Kupata thamani ya muhimu\(\displaystyle \int_C(x^2+y^2+z) \,ds\), ambapo\(C\) ni sehemu ya helix parameterized na\(\vecs r(t)=⟨\cos(2t),\sin(2t),2t⟩\),\(0≤t≤π\). Kumbuka kwamba kazi hii na Curve ni sawa na katika mfano uliopita; tofauti tu ni kwamba Curve imekuwa reparameterized ili wakati anaendesha mara mbili kwa haraka.

Suluhisho

Kama ilivyo kwa mfano uliopita, tunatumia Equation\ ref {eq12a} kukokotoa muhimu kwa heshima na\(t\). Kumbuka kuwa\(f(\vecs r(t))={\cos}^2(2t)+{\sin}^2(2t)+2t=2t+1\) na

\ [kuanza {align*}\ sqrt {{(x( t)))} ^2+ {(y( t))} ^2+ {(z( t))} ^2} &=\ sqrt {(-\ dhambi t+\ cos t+4)}\\ [4pt] &=22
\ mwisho {align*}\]

hivyo tuna

\[\begin{align*} \int_C(x^2+y^2+z)ds &=2\sqrt{2}\int_{0}^{\pi}(1+2t)dt\\[4pt] &=2\sqrt{2}\Big[t+t^2\Big]_0^{\pi} \\[4pt] &=2\sqrt{2}(\pi+{\pi}^2). \end{align*}\]

Kumbuka kwamba hii inakubaliana na jibu katika mfano uliopita. Kubadilisha parameterization haikubadilisha thamani ya mstari muhimu. Scalar line integrals ni huru ya parameterization, kwa muda mrefu kama Curve ni kupita hasa mara moja na parameterization.

Zoezi\(\PageIndex{3}\)

Tathmini mstari muhimu\(\displaystyle \int_C(x^2+yz) \,ds\),\(C\) wapi mstari na parameterization\(\vecs r(t)=⟨2t,5t,−t⟩\),\(0≤t≤10\). Repameterize C na parameterization\(s(t)=⟨4t,10t,−2t⟩\)\(0≤t≤5\), recalculate line muhimu\(\displaystyle \int_C(x^2+yz) \,ds\), na taarifa kwamba mabadiliko ya parameterization hakuwa na athari juu ya thamani ya muhimu.

Kidokezo

Tumia Equation\ ref {eq12a}.

Jibu

Wote line integrals sawa\(−\dfrac{1000\sqrt{30}}{3}\).

Sasa kwa kuwa tunaweza kutathmini integrals line, tunaweza kutumia yao kwa mahesabu ya urefu arc. Ikiwa\(f(x,y,z)=1\), basi

\[\begin{align*} \int_C f(x,y,z) \,ds &=\lim_{n\to\infty} \sum_{i=1}^{n} f(t_{i}^{*}) \,\Delta s_i \\[4pt] &=\lim_{n\to\infty} \sum_{i=1}^{n} \,\Delta s_i \\[4pt] &=\lim_{n\to\infty} \text{length} (C)\\[4pt] &=\text{length} (C). \end{align*}\]

Kwa hiyo,\(\displaystyle \int_C 1 \,ds\) ni urefu wa arc\(C\).

Mfano\(\PageIndex{4}\): Calculating Arc Length

Waya ina sura ambayo inaweza kuonyeshwa na parameterization\(\vecs r(t)=⟨\cos t,\sin t,\frac{2}{3} t^{3/2}⟩\),\(0≤t≤4\pi\). Pata urefu wa waya.

Suluhisho

Urefu wa waya hutolewa na\(\displaystyle \int_C 1 \,ds\), wapi\(C\) safu na parameterization\(\vecs r\). Kwa hiyo,

\[\begin{align*} \text{The length of the wire} &=\int_C 1 \,ds \\[4pt] &=\int_{0}^{4\pi} ||\vecs r′(t)||\,dt \\[4pt] &=\int_{0}^{4\pi} \sqrt{(−\sin t)^2+\cos^2 t+t}dt \\[4pt] &=\int_{0}^{4\pi} \sqrt{1+t} dt \\[4pt] &=\left.\dfrac{2{(1+t)}^{\frac{3}{2}}}{3} \right|_{0}^{4\pi} \\[4pt] &=\frac{2}{3}\left((1+4\pi)^{3/2}−1\right). \end{align*}\]

Zoezi\(\PageIndex{4}\)

Pata urefu wa waya na parameterization\(\vecs r(t)=⟨3t+1,4−2t,5+2t⟩\),\(0≤t≤4\).

Kidokezo

Kupata line muhimu ya moja juu ya Curve sambamba.

Jibu

\(4\sqrt{17}\)

vector line Integrals

Aina ya pili ya integrals line ni vector line integrals, ambayo sisi kuunganisha pamoja Curve kupitia shamba vector. Kwa mfano, basi

\[\vecs F(x,y,z)=P(x,y,z)\,\hat{\mathbf i}+Q(x,y,z)\,\hat{\mathbf j}+R(x,y,z)\,\hat{\mathbf k} \nonumber \]

kuwa kuendelea vector shamba kwa\(ℝ^3\) kuwa inawakilisha nguvu juu ya chembe, na basi\(C\) kuwa Curve laini katika\(ℝ^3\) zilizomo katika uwanja wa\(\vecs F\). Tunawezaje kukokotoa kazi iliyofanywa na\(\vecs F\) katika kusonga chembe pamoja\(C\)?

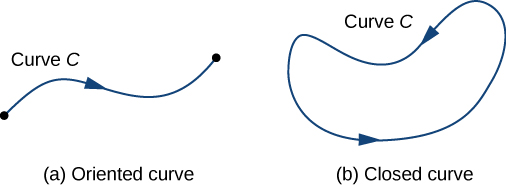
Ili kujibu swali hili, kwanza kumbuka kwamba chembe inaweza kusafiri kwa njia mbili kando ya pembe: mwelekeo wa mbele na mwelekeo wa nyuma. Kazi iliyofanywa na shamba la vector inategemea mwelekeo ambao chembe inahamia. Kwa hiyo, ni lazima tufafanue mwelekeo kando ya pembe\(C\); mwelekeo huo maalum huitwa mwelekeo wa curve. Mwelekeo maalum ni mwelekeo mzuri pamoja\(C\); mwelekeo kinyume ni mwelekeo hasi pamoja\(C\). Wakati\(C\) imepewa mwelekeo,\(C\) inaitwa Curve oriented (Kielelezo\(\PageIndex{5}\)). Kazi iliyofanywa kwenye chembe inategemea mwelekeo kando ya pembe ambayo chembe inahamia.

Curve imefungwa ni moja ambayo kuna parameterization\(\vecs r(t)\),\(a≤t≤b\), kama kwamba\(\vecs r(a)=\vecs r(b)\), na Curve ni kupita hasa mara moja. Kwa maneno mengine, parameterization ni moja kwa moja kwenye uwanja\((a,b)\).

Kielelezo\(\PageIndex{5}\): (a) Curve oriented kati ya pointi mbili. (b) Curve iliyofungwa iliyofungwa.

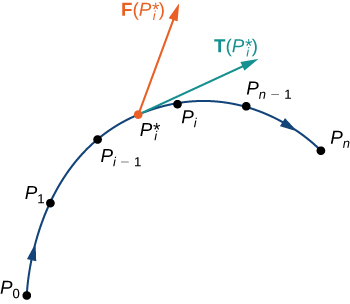
Hebu\(\vecs r(t)\) kuwa parameterization ya\(C\) kwa\(a≤t≤b\) vile kwamba Curve ni kupita hasa mara moja na chembe na hatua chembe katika mwelekeo chanya pamoja\(C\). Gawanya muda wa parameter\([a,b]\) ndani ya n\(0≤i≤n\) subinternations\([t_{i−1},t_i]\),, ya upana sawa. Eleza mwisho wa\(r(t_0)\),\(r(t_1)\),...,\(r(t_n)\) na\(P_0\),...,\(P_n\). Pointi\(P_i\)\(C\) hugawanywa katika vipande n. Eleza urefu wa kipande kutoka\(P_{i−1}\)\(P_i\) kwa\(\Delta s_i\). Kwa kila mmoja\(i\), chagua thamani\(t_i^*\) katika subinterval\([t_{i−1},t_i]\). Kisha, mwisho wa\(\vecs r(t_i^*)\) ni hatua katika kipande cha\(C\) kati\(P_{i−1}\) na\(P_i\) (Kielelezo\(\PageIndex{6}\)). Kama\(\Delta s_i\) ni ndogo, basi kama chembe hatua kutoka\(P_{i−1}\) kwa\(P_i\) pamoja\(C\), hatua takriban katika mwelekeo wa\(\vecs T(P_i)\), kitengo tangent vector katika mwisho wa\(\vecs r(t_i^*)\). Hebu\(P_i^*\) kuashiria mwisho wa\(\vecs r(t_i^*)\). Kisha, kazi iliyofanywa na uwanja wa vector nguvu katika kusonga chembe kutoka\(P_{i−1}\) kwa\(P_i\) ni\(\vecs F(P_i^*)·(\Delta s_i \vecs T(P_i^*))\), hivyo kazi ya jumla iliyofanywa pamoja\(C\) ni

\[\sum_{i=1}^n \vecs F(P_i^*)·(\Delta s_i \vecs T(P_i^*))=\sum_{i=1}^n \vecs F(P_i^*)·\vecs T(P_i^*)\,\Delta s_i. \nonumber \]

Kielelezo\(\PageIndex{6}\): Curve\(C\) imegawanywa katika vipande n, na hatua ndani ya kila kipande imechaguliwa. Bidhaa ya dot ya vector yoyote ya tangent katika kipande cha with na vector sambamba\(\vecs{F}\) inakadiriwa na\(\vecs{F}(P_i^*) \cdot \vecs{T}(P_i^*)\).

Kuruhusu urefu wa safu ya vipande vya\(C\) kupata kiholela ndogo kwa kuchukua kikomo kama\(n\rightarrow \infty\) inatupa kazi iliyofanywa na shamba katika kusonga chembe pamoja\(C\). Kwa hiyo, kazi iliyofanywa na\(\vecs{F}\) kusonga chembe katika mwelekeo mzuri pamoja\(C\) inaelezwa kama

\[W=\int_C \vecs{F} \cdot \vecs{T}\,ds, \nonumber \]

ambayo inatupa dhana ya mstari vector muhimu.

Ufafanuzi: Mstari Muhimu wa uwanja wa Vector

line vector muhimu ya uwanja vector\(\vecs{F}\) pamoja oriented laini Curve\(C\) ni

\[\int_C \vecs{F} \cdot \vecs{T}\, ds=\lim_{n\to\infty} \sum_{i=1}^{n} \vecs{F}(P_i^*) \cdot \vecs{T}(P_i^*)\Delta s_i \nonumber \]

kama kikomo kwamba ipo.

Kwa integrals mstari scalar, wala mwelekeo wala parameterization ya mambo Curve. Kwa muda mrefu kama curve inapita mara moja na parameterization, thamani ya mstari muhimu haibadilika. Pamoja na integrals line vector, mwelekeo wa Curve haina maana. Ikiwa tunafikiri juu ya mstari muhimu kama kazi ya kompyuta, basi hii ina maana: ikiwa unasimama juu ya mlima, basi nguvu ya mvuto ya Dunia inafanya kazi mbaya kwako. Ikiwa unatembea chini ya mlima kwa njia sawa, basi nguvu ya mvuto wa Dunia inafanya kazi nzuri kwako. Kwa maneno mengine, kugeuza njia hubadilisha thamani ya kazi kutoka hasi hadi chanya katika kesi hii. Kumbuka kwamba ikiwa\(C\) ni curve oriented, basi sisi basi\(−C\) kuwakilisha Curve sawa lakini kwa mwelekeo kinyume.

Kama ilivyo kwa integrals ya mstari wa scalar, ni rahisi kukokotoa mstari wa vector muhimu ikiwa tunaielezea kwa suala la kazi ya parameterization\(\vecs{r}\) na kutofautiana\(t\). Kutafsiri muhimu\(\displaystyle \int_C \vecs{F} \cdot \vecs{T}ds\) katika suala la\(t\), kumbuka kuwa kitengo tangent vector\(\vecs{T}\) pamoja\(C\) hutolewa na\(\vecs{T}=\dfrac{\vecs{r}′(t)}{‖\vecs{r}′(t)‖}\) (kuchukua\(‖\vecs{r}′(t)‖≠0\)). Kwa kuwa\(ds=‖\vecs r′(t)‖\,dt\), kama tulivyoona wakati wa kujadili integrals line scalar, tuna

\[\vecs F·\vecs T\,ds=\vecs F(\vecs r(t))·\dfrac{\vecs r′(t)}{‖\vecs r′(t)‖}‖\vecs r′(t)‖dt=\vecs F(\vecs r(t))·\vecs r′(t)\,dt. \nonumber \]

Hivyo, tuna formula zifuatazo kwa ajili ya kompyuta vector line integrals:

\[\int_C\vecs F·\vecs T\,ds=\int_a^b \vecs F(\vecs r(t))·\vecs r′(t)\,dt.\label{lineintformula} \]

Kwa sababu ya Equation\ ref {lineintformula}, sisi mara nyingi kutumia nukuu\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\) kwa mstari muhimu\(\displaystyle \int_C \vecs F·\vecs T\,ds\).

Ikiwa\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\), basi\(\dfrac{d\vecs{r}}{dt}\) inaashiria vector\(⟨x′(t),y′(t),z′(t)⟩\), na\(d\vecs{r} = \vecs r'(t)\,dt\).

Mfano\(\PageIndex{5}\): Evaluating a Vector Line Integral

Pata thamani ya muhimu\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), wapi\(C\) semicircle parameterized na\(\vecs{r}(t)=⟨\cos t,\sin t⟩\),\(0≤t≤\pi\) na\(\vecs F=⟨−y,x⟩\).

Suluhisho

Tunaweza kutumia Equation\ ref {lineintformula} kubadili kutofautiana ya ushirikiano kutoka\(s\) kwa\(t\). Sisi basi

\[\vecs F(\vecs r(t))=⟨−\sin t,\cos t⟩ \; \text{and} \; \vecs r′(t)=⟨−\sin t,\cos t⟩ . \nonumber \]

Kwa hiyo,

\[\begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &=\int_0^{\pi}⟨−\sin t,\cos t⟩·⟨−\sin t,\cos t⟩ \,dt \\[4pt] &=\int_0^{\pi} {\sin}^2 t+{\cos}^2 t \,dt \\[4pt] &=\int_0^{\pi}1 \,dt=\pi.\end{align*}\]

Angalia Kielelezo\(\PageIndex{7}\).

Kielelezo\(\PageIndex{7}\): Takwimu hii inaonyesha Curve\(\vecs r(t)=⟨\cos t,\,\sin t⟩\),\(0≤t≤\pi\) katika uwanja vector\(\vecs F=⟨−y,\,x⟩\).

Mfano\(\PageIndex{6}\): Reversing Orientation

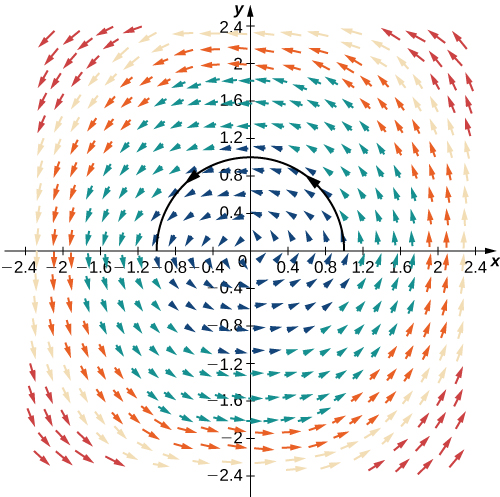
Pata thamani ya muhimu\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), wapi\(C\) semicircle parameterized na\(\vecs r(t)=⟨\cos (t+π),\sin t⟩\),\(0≤t≤\pi\) na\(\vecs F=⟨−y,x⟩\).

Suluhisho

Kumbuka kwamba hii ni tatizo sawa na Mfano\(\PageIndex{5}\), ila mwelekeo wa Curve imekuwa traversed. Katika mfano huu, parameterization huanza saa\(\vecs r(0)=⟨-1,0⟩\) na kuishia saa\(\vecs r(\pi)=⟨1,0⟩\). Kwa Equation\ ref {lineintformula},

\[\begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &=\int_0^{\pi} ⟨−\sin t,\cos (t+\pi)⟩·⟨−\sin (t+\pi), \cos t⟩dt\\[4pt] &=\int_0^{\pi}⟨−\sin t,−\cos t⟩·⟨\sin t,\cos t⟩dt\\[4pt] &=\int_{0}^{π}(−{\sin}^2 t−{\cos}^2 t)dt \\[4pt] &=\int_{0}^{\pi}−1dt\\[4pt] &=−\pi. \end{align*}\]

Kumbuka kwamba hii ni hasi ya jibu katika Mfano\(\PageIndex{5}\). Inafaa kuwa jibu hili ni hasi kwa sababu mwelekeo wa curve huenda kinyume na “mtiririko” wa shamba la vector.

Hebu\(C\) kuwa Curve oriented na basi\(-C\) kuashiria Curve huo lakini kwa mwelekeo kuachwa. Kisha, mifano miwili iliyopita inaonyesha ukweli wafuatayo:

\[\int_{-C} \vecs{F} \cdot d\vecs{r}=−\int_C\vecs{F} \cdot d\vecs{r}. \nonumber \]

Hiyo ni, kugeuza mwelekeo wa curve hubadilisha ishara ya mstari muhimu.

Zoezi\(\PageIndex{6}\)

Hebu\(\vecs F=x\,\hat{\mathbf i}+y \,\hat{\mathbf j}\) kuwa uwanja vector na basi\(C\) kuwa Curve na parameterization\(⟨t,t^2⟩\) kwa\(0≤t≤2\). Ambayo ni kubwa zaidi:\(\displaystyle \int_C\vecs F·\vecs T\,ds\) au\(\displaystyle \int_{−C} \vecs F·\vecs T\,ds\)?

Kidokezo

Fikiria kusonga njiani na kompyuta bidhaa dot\(\vecs F·\vecs T\) kama wewe kwenda.

Jibu

\[\int_C \vecs F·\vecs T \,ds \nonumber \]

Mwingine notation kiwango kwa ajili ya muhimu\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\) ni\(\displaystyle \int_C P\,dx+Q\,dy+R \,dz\). Katika nukuu hii,\(P,\, Q\), na\(R\) ni kazi, na tunadhani\(d\vecs{r}\) kama vector\(⟨dx,dy,dz⟩\). Ili kuhalalisha mkataba huu, kumbuka hilo\(d\vecs{r}=\vecs T\,ds=\vecs r′(t) \,dt=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\,dt\). Kwa hiyo,

\[\vecs{F} \cdot d\vecs{r}=⟨P,Q,R⟩·⟨dx,dy,dz⟩=P\,dx+Q\,dy+R\,dz. \nonumber \]

Ikiwa\(d\vecs{r}=⟨dx,dy,dz⟩\), basi\(\dfrac{dr}{dt}=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\), ambayo ina maana kwamba\(d\vecs{r}=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\,dt\). Kwa hiyo

\[\begin{align} \int_C \vecs{F} \cdot d\vecs{r} &=\int_C P\,dx+Q\,dy+R\,dz \\[4pt] &=\int_a^b\left(P\big(\vecs r(t)\big)\dfrac{dx}{dt}+Q\big(\vecs r(t)\big)\dfrac{dy}{dt}+R\big(\vecs r(t)\big)\dfrac{dz}{dt}\right)\,dt. \label{eq14}\end{align} \]

Mfano\(\PageIndex{7}\): Finding the Value of an Integral of the Form \(\displaystyle \int_C P\,dx+Q\,dy+R\,dz\)

Kupata thamani ya muhimu\(\displaystyle \int_C z\,dx+x\,dy+y\,dz\), ambapo\(C\) ni Curve parameterized na\(\vecs r(t)=⟨t^2,\sqrt{t},t⟩\),\(1≤t≤4\).

Suluhisho

Kama ilivyo kwa mifano yetu ya awali, kukokotoa mstari huu muhimu tunapaswa kufanya mabadiliko ya vigezo kuandika kila kitu katika suala la\(t\). Katika kesi hii, Equation\ ref {eq14} inatuwezesha kufanya mabadiliko haya:

\[\begin{align*} \int_C z\,dx+x\,dy+y\,dz &=\int_1^4 \left(t(2t)+t^2\left(\frac{1}{2\sqrt{t}}\right)+\sqrt{t}\right)\,dt \\[4pt] &=\int_1^4\left(2t^2+\frac{t^{3/2}}{2}+\sqrt{t}\right)\,dt \\[4pt] &={\left[\dfrac{2t^3}{3}+\dfrac{t^{5/2}}{5}+\dfrac{2t^{3/2}}{3} \right]}_{t=1}^{t=4} \\[4pt] &=\dfrac{793}{15}.\end{align*}\]

Zoezi\(\PageIndex{7}\)

Kupata thamani ya\(\displaystyle \int_C 4x\,dx+z\,dy+4y^2\,dz\), ambapo\(C\) ni Curve parameterized na\(\vecs r(t)=⟨4\cos(2t),2\sin(2t),3⟩\),\(0≤t≤\dfrac{\pi}{4}\).

Kidokezo

Andika muhimu katika suala la\(t\) kutumia Equation\ ref {eq14}.

Jibu

\(−26\)

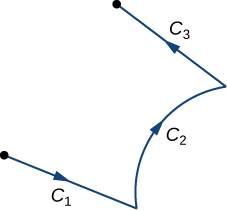
Tumejifunza jinsi ya kuunganisha curves laini oriented. Sasa, tuseme kwamba\(C\) ni Curve oriented kwamba si laini, lakini inaweza kuandikwa kama muungano wa finitely curves wengi laini. Katika kesi hii, tunasema kwamba\(C\) ni piecewise laini Curve. Kuwa sahihi, Curve\(C\) ni piecewise laini kama\(C\) inaweza kuandikwa kama muungano wa n curves\(C_1\) laini,,...,\(C_n\) kama kwamba endpoint ya\(C_i\) ni mwanzo wa\(C_{i+1}\) (Kielelezo\(\PageIndex{8}\)).\(C_2\) Wakati curves\(C_i\) kukidhi hali ya kuwa endpoint ya\(C_i\) ni mwanzo wa\(C_{i+1}\), tunaandika muungano wao kama\(C_1+C_2+⋯+C_n\).

Kielelezo\(\PageIndex{8}\): muungano wa\(C_1\),\(C_2\),\(C_3\) ni piecewise laini Curve.

Theorem inayofuata inafupisha mali kadhaa muhimu za integrals ya mstari wa vector.

Theorem: Mali ya Vector Line Integrals

Hebu\(\vecs F\) na\(\vecs G\) uwe na mashamba ya vector yanayoendelea na vikoa ambavyo vinajumuisha safu ya laini iliyoelekezwa\(C\). Kisha

1. \(\displaystyle \int_C(\vecs F+\vecs G)·d\vecs{r}=\int_C \vecs{F} \cdot d\vecs{r}+\int_C \vecs G·d\vecs{r}\)
2. \(\displaystyle \int_C k\vecs{F} \cdot d\vecs{r}=k\int_C \vecs{F} \cdot d\vecs{r}\), wapi\(k\) mara kwa mara
3. \(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}=\int_{−C}\vecs{F} \cdot d\vecs{r}\)
4. Tuseme badala kwamba\(C\) ni piecewise laini Curve katika nyanja ya\(\vecs F\)\(C=C_1+C_2+⋯+C_n\) na\(\vecs G\), ambapo na\(C_1,C_2,…,C_n\) ni laini curves vile kwamba endpoint ya\(C_i\) ni mwanzo wa\(C_{i+1}\). Kisha

   \[\int_C \vecs F·d\vecs{r}=\int_{C_1} \vecs F·d\vecs{r}+\int_{C_2} \vecs F·d\vecs{r}+⋯+\int_{C_n} \vecs F·d\vecs{r}. \nonumber \]

Angalia kufanana kati ya vitu hivi na mali ya integrals moja-variable. Mali i. na ii. kusema kwamba mstari integrals ni linear, ambayo ni kweli ya integrals single-variable pia. Mali ii. anasema kuwa kugeuza mwelekeo wa curve hubadilisha ishara ya muhimu. Ikiwa tunadhani muhimu kama kompyuta kazi iliyofanywa kwenye chembe inayosafiri pamoja\(C\), basi hii inafanya maana. Ikiwa chembe inakwenda nyuma badala ya mbele, basi thamani ya kazi iliyofanywa ina ishara tofauti. Hii ni sawa na equation\(\displaystyle \int_a^b f(x)\,dx=−\int_b^af(x)\,dx\). Hatimaye, ikiwa\([a_1,a_2]\)\([a_2,a_3]\),...,\([a_{n−1},a_n]\) ni vipindi, basi

\[\int_{a_1}^{a_n}f(x) \,dx=\int_{a_1}^{a_2}f(x)\,dx+\int_{a_1}^{a_3}f(x)\,dx+⋯+\int_{a_{n−1}}^{a_n} f(x)\,dx, \nonumber \]

ambayo ni sawa na mali iv.

Mfano\(\PageIndex{8}\): Using Properties to Compute a Vector Line Integral

Pata thamani ya muhimu\(\displaystyle \int_C \vecs F·\vecs T \,ds\), wapi\(C\) mstatili (unaoelekezwa kinyume chake) katika ndege yenye vipeo,\((0,0)\)\((2,0)\), na\((2,1)\)\((0,1)\), na wapi\(\vecs F=⟨x−2y,y−x⟩\) (Kielelezo\(\PageIndex{9}\)).

Kielelezo\(\PageIndex{9}\): Mstatili na vector shamba kwa Mfano\(\PageIndex{8}\).

Suluhisho

Kumbuka kuwa Curve\(C\) ni muungano wa pande zake nne, na kila upande ni laini. Kwa hiyo\(C\) ni laini ya kipande. Hebu\(C_1\) kuwakilisha upande kutoka\((0,0)\) kwa\((2,0)\), hebu\(C_2\) kuwakilisha upande kutoka\((2,0)\) kwa\((2,1)\), basi\(C_3\) kuwakilisha upande kutoka\((2,1)\) kwa\((0,1)\), na basi\(C_4\) kuwakilisha upande kutoka\((0,1)\) kwa\((0,0)\) (Kielelezo\(\PageIndex{9}\)). Kisha,

\[\int_C \vecs F·\vecs T \,dr=\int_{C_1} \vecs F·\vecs T \,dr+\int_{C_2} \vecs F·\vecs T \,dr+\int_{C_3} \vecs F·\vecs T \,dr+\int_{C_4} \vecs F·\vecs T \,dr. \nonumber \]

Tunataka kukokotoa kila moja ya integrals nne upande wa kulia kwa kutumia Equation\ ref {eq12a}. Kabla ya kufanya hivyo, tunahitaji parameterization ya kila upande wa mstatili. Hapa ni parameterizations nne (kumbuka kwamba wao hupitia\(C\) kinyume chake):

\[\begin{align*} C_1&: ⟨t,0⟩,0≤t≤2\\[4pt] C_2&: ⟨2,t⟩, 0≤t≤1 \\[4pt] C_3&: ⟨2−t,1⟩, 0≤t≤2\\[4pt] C_4&: ⟨0,1−t⟩, 0≤t≤1. \end{align*}\]

Kwa hiyo,

\[\begin{align*} \int_{C_1} \vecs F·\vecs T \,dr &=\int_0^2 \vecs F(\vecs r(t))·\vecs r′(t) \,dt \\[4pt] &=\int_0^2 ⟨t−2(0),0−t⟩·⟨1,0⟩ \,dt=\int_0^2 t \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}\Big]_0^2=2. \end{align*}\]

Angalia kwamba thamani ya muhimu hii ni chanya, ambayo haipaswi kushangaza. Tunapohamia kando ya pembe\(C_1\) kutoka kushoto kwenda kulia, harakati zetu inapita katika mwelekeo wa jumla wa shamba la vector yenyewe. Katika hatua yoyote pamoja\(C_1\), vector tangent kwa Curve na vector sambamba katika shamba kuunda angle ambayo ni chini ya 90°. Kwa hiyo, vector tangent na vector nguvu na chanya dot bidhaa zote pamoja\(C_1\), na mstari muhimu itakuwa na thamani chanya.

Mahesabu ya integrals nyingine tatu za mstari hufanyika sawa:

\[\begin{align*} \int_{C_2} \vecs{F} \cdot d\vecs{r} &=\int_{0}^{1}⟨2−2t,t−2⟩·⟨0,1⟩ \,dt \\[4pt] &=\int_{0}^{1} (t−2) \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}−2t\Big]_0^1=−\dfrac{3}{2}, \end{align*}\]

\[\begin{align*} \int_{C_3} \vecs F·\vecs T \,ds &=\int_0^2⟨(2−t)−2,1−(2−t)⟩·⟨−1,0⟩ \,dt \\[4pt] &=\int_0^2t \,dt=2, \end{align*}\]

na

\[\begin{align*} \int_{C_4} \vecs{F} \cdot d\vecs{r} &=\int_0^1⟨−2(1−t),1−t⟩·⟨0,−1⟩ \,dt \\[4pt] &=\int_0^1(t−1) \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}−t\Big]_0^1=−\dfrac{1}{2}. \end{align*}\]

Hivyo, tuna\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}=2\).

Zoezi\(\PageIndex{8}\)

Tumia mstari muhimu\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), wapi uwanja\(\vecs F\) wa vector\(⟨y^2,2xy+1⟩\) na\(C\) ni pembetatu na vipeo\((0,0)\),\((4,0)\), na\((0,5)\), inaelekezwa kinyume chake.

Kidokezo

Andika pembetatu kama muungano wa pande zake tatu, kisha uhesabu mahesabu ya mstari wa tatu tofauti.

Jibu

0

Matumizi ya Line Integrals

Scalar line integrals na maombi mengi. Wanaweza kutumika kuhesabu urefu au wingi wa waya, eneo la uso wa karatasi ya urefu uliopewa, au uwezo wa umeme wa waya iliyoshtakiwa kutokana na wiani wa malipo ya mstari. Vector line integrals ni muhimu sana katika fizikia. Zinaweza kutumika kuhesabu kazi iliyofanywa kwenye chembe inapotembea kupitia uwanja wa nguvu, au kiwango cha mtiririko wa maji kwenye pembe. Hapa, tunahesabu wingi wa waya kwa kutumia mstari wa scalar muhimu na kazi iliyofanywa na nguvu kwa kutumia mstari wa vector muhimu.

Tuseme kwamba kipande cha waya kinaelekezwa na Curve C katika nafasi. Uzito kwa urefu wa kitengo (wiani wa mstari) wa waya ni kazi inayoendelea\(\rho(x,y,z)\). Tunaweza kuhesabu wingi wa waya kwa kutumia mstari wa scalar muhimu\(\displaystyle \int_C \rho(x,y,z) \,ds\). Sababu ni kwamba wingi ni wiani unaoongezeka kwa urefu, na kwa hiyo wiani wa kipande kidogo cha waya unaweza kukadiriwa na\(\rho(x^*,y^*,z^*) \,\Delta s\) kwa hatua fulani\((x^*,y^*,z^*)\) katika kipande. Kuruhusu urefu wa vipande kupungua hadi sifuri na kikomo huzaa mstari muhimu\(\displaystyle \int_C \rho(x,y,z) \,ds\).

Mfano\(\PageIndex{9}\): Calculating the Mass of a Wire

Tumia wingi wa spring kwa sura ya curve iliyowekwa na\(⟨t,2\cos t,2\sin t⟩\),\(0≤t≤\dfrac{\pi}{2}\), na kazi ya wiani iliyotolewa na\(\rho(x,y,z)=e^x+yz\) kg/m (Kielelezo\(\PageIndex{10}\)).

Kielelezo\(\PageIndex{10}\): waya kutoka Mfano\(\PageIndex{9}\).

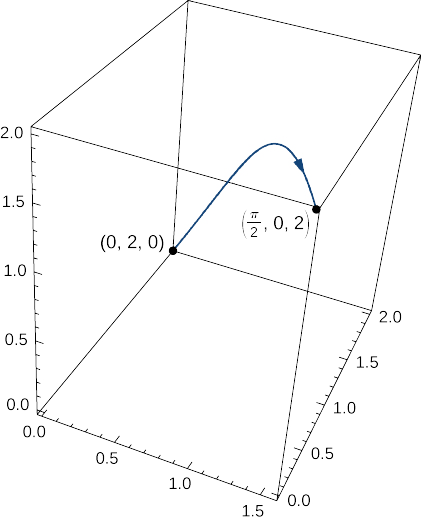
Suluhisho

Ili kuhesabu wingi wa chemchemi, tunapaswa kupata thamani ya mstari wa scalar muhimu\(\displaystyle \int_C(e^x+yz)\,ds\), wapi\(C\) helix iliyotolewa. Ili kuhesabu jambo hili muhimu, tunaandika kwa\(t\) kutumia Equation\ ref {eq12a}:

\[\begin{align*} \int_C \left(e^x+yz\right) \,ds &=\int_0^{\tfrac{\pi}{2}} \left((e^t+4\cos t\sin t)\sqrt{1+(−2\cos t)^2+(2\sin t)^2}\right)\,dt\\[4pt] &=\int_0^{\tfrac{\pi}{2}}\left((e^t+4\cos t\sin t)\sqrt{5}\right) \,dt \\[4pt] &=\sqrt{5}\Big[e^t+2\sin^2 t\Big]_{t=0}^{t=\pi/2}\\[4pt] &=\sqrt{5}(e^{\pi/2}+1). \end{align*}\]

Kwa hiyo, wingi ni\(\sqrt{5}(e^{\pi/2}+1)\) kilo.

Zoezi\(\PageIndex{9}\)

Tumia wingi wa spring kwa sura ya helix iliyowekwa na\(\vecs r(t)=⟨\cos t,\sin t,t⟩\),\(0≤t≤6\pi\), na kazi ya wiani iliyotolewa na\(\rho (x,y,z)=x+y+z\) kg/m.

Kidokezo

Tumia mstari muhimu wa\(\rho\) juu ya pembe na parameterization\(\vecs r\).

Jibu

\(18\sqrt{2}{\pi}^2\)kilo

Wakati sisi kwanza defined vector line integrals, tulitumia dhana ya kazi ya kuhamasisha ufafanuzi. Kwa hiyo, haishangazi kwamba kuhesabu kazi iliyofanywa na uwanja wa vector anayewakilisha nguvu ni matumizi ya kawaida ya integrals ya mstari wa vector. Kumbuka kwamba kama kitu hatua pamoja Curve\(C\) katika uwanja nguvu\(\vecs F\), basi kazi required kwa hoja kitu ni iliyotolewa na\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\).

Mfano\(\PageIndex{10}\): ​​​​​​Calculating Work

Kiasi gani kazi inahitajika kwa hoja kitu katika vector nguvu shamba\(\vecs F=⟨yz,xy,xz⟩\) njiani\(\vecs r(t)=⟨t^2,t,t^4⟩,\, 0≤t≤1?\) Angalia Kielelezo\(\PageIndex{11}\).

Suluhisho

Hebu\(C\) ueleze njia iliyotolewa. Tunahitaji kupata thamani ya\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\). Ili kufanya hivyo, tunatumia Equation\ ref {lineintformula}:

\[\begin{align*}\int_C \vecs{F} \cdot d\vecs{r} &=\int_0^1(⟨t^5,t^3,t^6⟩·⟨2t,1,4t^3⟩) \,dt \\[4pt] &=\int_0^1(2t^6+t^3+4t^9) \,dt \\[4pt] &={\Big[\dfrac{2t^7}{7}+\dfrac{t^4}{4}+\dfrac{2t^{10}}{5}\Big]}_{t=0}^{t=1}=\dfrac{131}{140}\;\text{units of work}. \end{align*}\]

Kielelezo\(\PageIndex{11}\): Curve na vector shamba kwa Mfano\(\PageIndex{10}\).

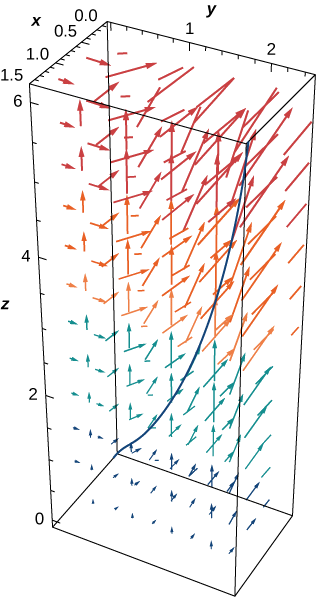
Flux

Sisi kufunga sehemu hii kwa kujadili dhana mbili muhimu kuhusiana na mstari integrals: flux katika Curve ndege na mzunguko pamoja Curve ndege. Flux hutumiwa katika maombi ya kuhesabu mtiririko wa maji katika pembe, na dhana ya mzunguko ni muhimu kwa kuashiria mashamba ya kihafidhina ya gradient kwa suala la mstari wa mstari. Dhana hizi zote mbili hutumiwa sana katika sura hii yote. Wazo la kuenea ni muhimu hasa kwa theorem ya Green, na kwa vipimo vya juu kwa theorem ya Stokes na theorem ya tofauti.

Hebu\(C\) kuwa Curve ndege na basi\(\vecs F\) kuwa uwanja vector katika ndege. Fikiria\(C\) ni membrane ambayo maji hutoka, lakini\(C\) haizuii mtiririko wa maji. Kwa maneno mengine,\(C\) ni membrane idealized asiyeonekana kwa maji. Tuseme\(\vecs F\) inawakilisha uwanja wa kasi wa maji. Tunawezaje kupima kiwango ambacho maji yanavuka\(C\)?

Kumbuka kwamba mstari muhimu wa\(\vecs F\) pamoja\(C\) ni\(\displaystyle \int_C \vecs F·\vecs T \,ds\) - kwa maneno mengine, mstari muhimu ni bidhaa ya dot ya shamba la vector na vector ya kitengo cha tangential kuhusiana na urefu wa arc. Kama sisi kuchukua nafasi ya kitengo tangential vector na kitengo kawaida vector\(\vecs N(t)\) na badala compute muhimu\(\int_C \vecs F·\vecs N \,ds\), sisi kuamua flux hela\(C\). Ili kuwa sahihi, ufafanuzi wa muhimu\(\displaystyle \int_C \vecs F·\vecs N \,ds\) ni sawa na muhimu\(\displaystyle \int_C \vecs F·\vecs T \,ds\), isipokuwa\(\vecs T\) katika jumla ya Riemann inabadilishwa na\(\vecs N\). Kwa hiyo, flux katika\(C\) hufafanuliwa kama

\[\int_C \vecs F·\vecs N \,ds=\lim_{n\to\infty}\sum_{i=1}^{n} \vecs F(P_i^*)·\vecs N(P_i^*)\,\Delta s_i, \nonumber \]

ambapo\(P_i^*\) na\(\Delta s_i\) hufafanuliwa kama walikuwa kwa ajili ya muhimu\(\displaystyle \int_C \vecs F·\vecs T \,ds\). Kwa hiyo, muhimu ya kutosha ni muhimu ambayo ni perpendicular kwa mstari wa vector muhimu, kwa sababu\(\vecs N\) na\(\vecs T\) ni vectors perpendicular.

Ikiwa\(\vecs F\) ni uwanja wa kasi wa maji na\(C\) ni pembe inayowakilisha utando, basi mtiririko wa\(\vecs F\) hela\(C\) ni wingi wa maji yanayotembea\(C\) kwa wakati wa kitengo, au kiwango cha mtiririko.

Zaidi rasmi, hebu\(C\) kuwa ndege Curve parameterized na\(\vecs r(t)=⟨x(t),\,y(t)⟩\),\(a≤t≤b\). Hebu\(\vecs n(t)=⟨y′(t),\,−x′(t)⟩\) kuwa vector ambayo ni ya kawaida kwa\(C\) mwisho wa\(\vecs r(t)\) na pointi ya haki kama sisi kupita\(C\) katika mwelekeo chanya (Kielelezo\(\PageIndex{12}\)). Kisha,\(\vecs N(t)=\dfrac{\vecs n(t)}{‖\vecs n(t)‖}\) ni kitengo kawaida vector kwa\(C\) saa endpoint ya\(\vecs r(t)\) kwamba pointi na haki kama sisi traverse\(C\).

Ufafanuzi: Flux

Flux ya\(\vecs F\) hela\(C\) ni mstari muhimu

\[\int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖} \,ds. \nonumber \]

Kielelezo\(\PageIndex{12}\): Flux ya uwanja vector\(\vecs F\) katika Curve\(C\) ni computed na muhimu sawa na mstari vector muhimu.

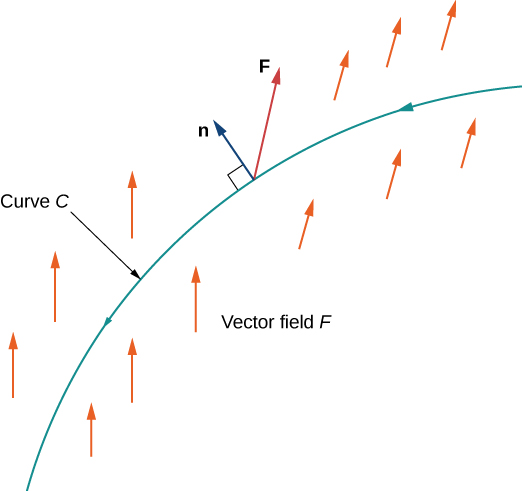
Sasa tunatoa formula ya kuhesabu mtiririko katika pembe. Fomula hii ni sawa na formula inayotumiwa kuhesabu mstari wa vector muhimu (angalia Equation\ ref {lineintformula}).

Theorem: Kuhesabu Flux Katika Curve

Hebu\(\vecs F\) kuwa uwanja vector na basi\(C\) kuwa Curve laini na parameterization\(r(t)=⟨x(t),y(t)⟩\),\(a≤t≤b\) .Let\(\vecs n(t)=⟨y′(t),−x′(t)⟩\). Flux ya\(\vecs F\) hela\(C\) ni

\[\int_C \vecs F·\vecs N\,ds=\int_a^b\vecs F(\vecs r(t))·\vecs n(t) \,dt. \label{eq84} \]

Ushahidi

Kabla ya kupata formula, kumbuka kuwa

\[‖\vecs n(t)‖=‖⟨y′(t),−x′(t)⟩‖=\sqrt{{(y′(t))}^2+{(x′(t))}^2}=‖\vecs r′(t)‖. \nonumber \]

Kwa hiyo,

\[\begin{align*}\int_C \vecs F·\vecs N \,ds &=\int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖} \,ds \\[4pt] &=\int_a^b \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖}‖\vecs r′(t)‖ \,dt \\[4pt] &=\int_a^b \vecs F(\vecs r(t))·\vecs n(t) \,dt. \end{align*}\]

\(\square\)

Mfano\(\PageIndex{11}\): Flux across a Curve

Tumia mzunguko wa mzunguko wa\(\vecs F=⟨2x,2y⟩\) kitengo kilichoelekezwa kinyume chake (Kielelezo\(\PageIndex{13}\)).

Kielelezo\(\PageIndex{13}\): mduara kitengo katika uwanja vector\(\vecs F=⟨2x,\,2y⟩\).

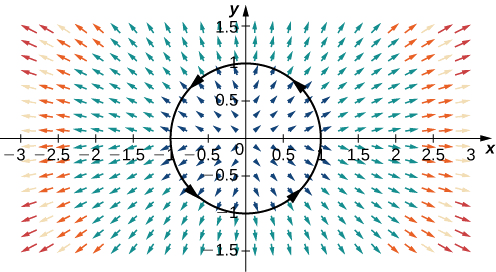
Suluhisho

Ili kuhesabu mtiririko, sisi kwanza tunahitaji parameterization ya mduara wa kitengo. Tunaweza kutumia parameterization kiwango\(\vecs r(t)=⟨\cos t,\sin t⟩\),\(0≤t≤2\pi\). Vector kawaida kwa mduara kitengo ni\(⟨\cos t,\sin t⟩\). Kwa hiyo, flux ni

\[\begin{align*} \int_C \vecs F·\vecs N \,ds &=\int_0^{2\pi}⟨2\cos t,2\sin t⟩·⟨\cos t,\sin t⟩ \,dt\\[4pt] &=\int_0^{2\pi}(2{\cos}^2t+2{\sin}^2t) \,dt \\[4pt] &=2\int_0^{2\pi}({\cos}^2t+{\sin}^2t) \,dt \\[4pt] &=2\int_0^{2\pi} \,dt=4\pi.\end{align*}\]

Zoezi\(\PageIndex{11}\)

Tumia mzunguko wa\(\vecs F=⟨x+y,2y⟩\) sehemu ya mstari kutoka\((0,0)\) kwa\((2,3)\), ambapo pembe inaelekezwa kutoka kushoto kwenda kulia.

Kidokezo

Tumia Equation\ ref {eq84}.

Jibu

\(3/2\)

Hebu\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩\) kuwa uwanja wa vector mbili-dimensional. Kumbuka kwamba muhimu wakati mwingine\(\displaystyle \int_C \vecs F·\vecs T \,ds\) imeandikwa kama\(\displaystyle \int_C P\,dx+Q\,dy\). Kwa mfano, flux wakati mwingine\(\displaystyle \int_C \vecs F·\vecs N \,ds\) imeandikwa katika notation\(\displaystyle \int_C −Q\,dx+P\,dy\), kwa sababu kitengo kawaida vector\(\vecs N\) ni perpendicular kwa kitengo tangent\(\vecs T\). Kupokezana vector\(d\vecs{r}=⟨dx,dy⟩\) na matokeo 90° katika vector\(⟨dy,−dx⟩\). Kwa hiyo, mstari muhimu katika Mfano\(\PageIndex{8}\) unaweza kuandikwa kama\(\displaystyle \int_C −2y\,dx+2x\,dy\).

Mzunguko

Sasa kwa kuwa tumeelezea kuenea, tunaweza kugeuka mawazo yetu kwa mzunguko. Mstari muhimu wa shamba la vector\(\vecs F\) pamoja na curve iliyofungwa imefungwa inaitwa mzunguko wa\(\vecs F\) pamoja\(C\). Mzunguko wa mstari wa mzunguko una nukuu yao wenyewe:\(\oint_C \vecs F·\vecs T \,ds\). Mduara juu ya ishara muhimu inaashiria kwamba\(C\) ni “mviringo” kwa kuwa haina mwisho. Mfano\(\PageIndex{5}\) unaonyesha hesabu ya mzunguko.

Ili kuona wapi mzunguko wa muda unatoka na kile kinachopima, hebu\(\vecs v\) kuwakilisha shamba la kasi la maji na uache\(C\) kuwa safu iliyofungwa iliyofungwa. Kwa hatua fulani\(P\), karibu na mwelekeo wa\(\vecs v(P)\) ni mwelekeo wa\(\vecs T(P)\), thamani kubwa ya bidhaa ya dot\(\vecs v(P)·\vecs T(P)\). thamani ya juu ya\(\vecs v(P)·\vecs T(P)\) hutokea wakati wadudu wawili ni akizungumzia katika halisi mwelekeo huo; thamani ya chini ya\(\vecs v(P)·\vecs T(P)\) hutokea wakati wadudu wawili ni akizungumzia katika mwelekeo kinyume. Hivyo, thamani ya mzunguko\(\oint_C \vecs v·\vecs T \,ds\) inachukua tabia ya maji kuhamia katika mwelekeo wa\(C\).

Mfano\(\PageIndex{12}\): Calculating Circulation

Hebu\(\vecs F=⟨−y,\,x⟩\) kuwa uwanja vector kutoka Mfano\(\PageIndex{3}\) na basi\(C\) kuwakilisha kitengo mduara oriented kinyume chake. Tumia mzunguko wa\(\vecs F\) pamoja\(C\).

Suluhisho

Tunatumia parameterization ya kawaida ya mduara wa kitengo:\(\vecs r(t)=⟨\cos t,\sin t⟩\),\(0≤t≤2\pi\). Kisha,\(\vecs F(\vecs r(t))=⟨−\sin t,\cos t⟩\) na\(\vecs r′(t)=⟨−\sin t,\cos t⟩\). Kwa hiyo, mzunguko wa\(\vecs F\) pamoja\(C\) ni

\[\begin{align*} \oint_C \vecs F·\vecs T \,ds &=\int_0^{2\pi}⟨−\sin t,\cos t⟩·⟨−\sin t,\cos t⟩ \,dt \\[4pt] &=\int_0^{2\pi} ({\sin}^2 t+{\cos}^2 t) \,dt \\[4pt] &=\int_0^{2\pi} \,dt=2\pi \;\text{units of work}. \end{align*}\]

Angalia kwamba mzunguko ni chanya. Sababu ya hii ni kwamba mwelekeo wa\(C\) “mtiririko” na mwelekeo wa\(\vecs F\). Wakati wowote kando ya mduara, vector tangent na vector kutoka\(\vecs F\) fomu angle ya chini ya 90°, na hivyo sambamba dot bidhaa ni chanya.

Katika Mfano\(\PageIndex{12}\), nini kama tulikuwa oriented kitengo mduara clockwise? Tunaashiria mduara wa kitengo unaoelekezwa saa moja kwa moja na\(−C\). Kisha

\[\oint_{−C} \vecs F·\vecs T \,ds=−\oint_C \vecs F·\vecs T \,ds=−2\pi \;\text{units of work}. \nonumber \]

Angalia kwamba mzunguko ni hasi katika kesi hii. Sababu ya hii ni kwamba mwelekeo wa Curve inapita dhidi ya mwelekeo wa\(\vecs F\).

Zoezi\(\PageIndex{12}\)

Tumia mzunguko wa\(\vecs F(x,y)=⟨−\dfrac{y}{x^2+y^2},\,\dfrac{x}{x^2+y^2}⟩\) kando ya mduara wa kitengo unaoelekezwa kinyume chake.

Kidokezo

Tumia Equation\ ref {eq84}.

Jibu

\(2\pi\)vitengo vya kazi

Mfano\(\PageIndex{13}\): Calculating Work

Tumia kazi iliyofanyika kwenye chembe inayovuka mduara\(C\) wa radius 2 unaozingatia asili, iliyoelekezwa kinyume chake, na shamba\(\vecs F(x,y)=⟨−2,\,y⟩\). Tuseme chembe kuanza harakati zake katika\((1,\,0)\).

Suluhisho

Kazi iliyofanywa na\(\vecs F\) chembe ni mzunguko wa\(\vecs F\) pamoja\(C\):\(\oint_C \vecs F·\vecs T \,ds\). Tunatumia parameterization\(\vecs r(t)=⟨2\cos t,\,2\sin t⟩\),\(0≤t≤2\pi\) kwa\(C\). Kisha,\(\vecs r′(t)=⟨−2\sin t,\,2\cos t⟩\) na\(\vecs F(\vecs r(t))=⟨−2,\,2\sin t⟩\). Kwa hiyo, mzunguko wa\(\vecs F\) pamoja\(C\) ni

\[\begin{align*} \oint_C \vecs F·\vecs T \,ds &=\int_0^{2\pi} ⟨−2,2\sin t⟩·⟨−2\sin t,2\cos t⟩ \,dt\\[4pt] &=\int_0^{2\pi} (4\sin t+4\sin t\cos t) \,dt\\[4pt] &={\Big[−4\cos t+4{\sin}^2 t\Big]}_0^{2\pi}\\[4pt] &=\left(−4\cos(2\pi)+2{\sin}^2(2\pi)\right)−\left(−4\cos(0)+4{\sin}^2(0)\right)\\[4pt] &=−4+4=0\;\text{units of work}.\end{align*}\]

Shamba la nguvu hufanya kazi ya sifuri kwenye chembe.

Angalia kwamba mzunguko wa\(\vecs F\) pamoja\(C\) ni sifuri. Zaidi ya hayo, taarifa kwamba tangu\(\vecs F\) ni gradient ya\(f(x,y)=−2x+\dfrac{y^2}{2}\),\(\vecs F\) ni kihafidhina. Tunathibitisha katika sehemu ya baadaye kwamba chini ya hali fulani pana, mzunguko wa shamba la vector la kihafidhina pamoja na safu iliyofungwa ni sifuri.

Zoezi\(\PageIndex{14}\)

Tumia kazi iliyofanywa na shamba\(\vecs F(x,y)=⟨2x,\,3y⟩\) kwenye chembe inayovuka mduara wa kitengo. Kudhani chembe huanza harakati zake katika\((−1,\,0)\).

Kidokezo

Tumia Equation\ ref {eq84}.

Jibu

\(0\)vitengo vya kazi

Dhana muhimu

• Mipangilio ya mstari huzalisha dhana ya moja-variable muhimu kwa vipimo vya juu. Uwanja wa ushirikiano katika sehemu moja ya kutofautiana ni sehemu ya mstari kando ya\(x\) -axis, lakini uwanja wa ushirikiano katika mstari muhimu ni safu katika ndege au katika nafasi.
• Ikiwa\(C\) ni safu, basi urefu wa\(C\) ni\(\displaystyle \int_C \,ds\).
• Kuna aina mbili za mstari muhimu: integrals line scalar na integrals line vector. Scalar line integrals inaweza kutumika kwa mahesabu ya wingi wa waya; vector line integrals inaweza kutumika kwa mahesabu ya kazi kufanyika kwenye chembe kusafiri kupitia shamba.
• Scalar line integrals inaweza kuhesabiwa kwa kutumia Equation\ ref {eq12a}; vector line integrals inaweza kuhesabiwa kwa kutumia Equation\ ref {lineintformula}.
• Dhana mbili muhimu zilizoelezwa kwa suala la mstari wa mstari ni flux na mzunguko. Flux hupima kiwango ambacho shamba linavuka mstari uliopewa; mzunguko hupima tabia ya shamba kuhamia katika mwelekeo sawa na curve iliyofungwa iliyotolewa.

Mlinganyo muhimu

• Kuhesabu mstari wa scalar muhimu
  \(\displaystyle \int_C f(x,y,z) \,ds=\int_a^bf(\vecs r(t))\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} \,dt\)
• Kuhesabu mstari wa vector muhimu
  \(\displaystyle \int_C \vecs F·d\vecs{r}=\int_C \vecs F·\vecs T \,ds=\int_a^b\vecs F(\vecs r(t))·\vecs r′(t)\,dt\)
  au
  \(\displaystyle \int_C P\,dx+Q\,dy+R\,dz=\int_a^b \left(P\big(\vecs r(t)\big)\dfrac{dx}{dt}+Q\big(\vecs r(t)\big)\dfrac{dy}{dt}+R\big(\vecs r(t)\big)\dfrac{dz}{dt}\right) \,dt\)
• Kuhesabu mtiririko
  \(\displaystyle \int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖}\,ds=\int_a^b \vecs F(\vecs r(t))·\vecs n(t) \,dt\)

faharasa

mzunguko

tabia ya maji ya kuhamia katika mwelekeo wa Curve\(C\). Ikiwa\(C\) ni safu iliyofungwa, basi mzunguko wa\(\vecs F\) pamoja\(C\) ni mstari muhimu\(∫_C \vecs F·\vecs T \,ds\), ambayo sisi pia inaashiria\(∮_C\vecs F·\vecs T \,ds\).

Curve imefungwa

Curve ambayo kuna parameterization\(\vecs r(t), a≤t≤b\), kama vile\(\vecs r(a)=\vecs r(b)\), na curve ni kupita hasa mara moja

flux

kiwango cha maji yanayotembea kwenye pembe katika uwanja wa vector; mtiririko wa shamba la vector\(\vecs F\) katika Curve ya ndege\(C\) ni mstari muhimu\(∫_C \vecs F·\frac{\vecs n(t)}{‖\vecs n(t)‖} \,ds\)

mstari muhimu

muhimu ya kazi pamoja Curve katika ndege au katika nafasi

mwelekeo wa curve

mwelekeo wa Curve\(C\) ni mwelekeo maalum wa\(C\)

kipande kimoja laini curve

Curve oriented ambayo si laini, lakini inaweza kuandikwa kama muungano wa curves finitely wengi laini

scalar line muhimu

mstari wa scalar muhimu wa kazi\(f\) pamoja\(C\) na curve kuhusiana na urefu wa arc ni muhimu\(\displaystyle \int_C f\,ds\), ni muhimu ya kazi ya scalar\(f\) pamoja na Curve katika ndege au katika nafasi; muhimu kama hiyo inaelezwa kwa suala la jumla ya Riemann, kama ni muhimu moja ya kutofautiana

vector line muhimu

mstari wa vector muhimu wa uwanja wa vector\(\vecs F\) pamoja na Curve\(C\) ni muhimu ya bidhaa ya dot ya\(\vecs F\) na kitengo tangent vector\(\vecs T\) ya kuhusiana\(C\) na urefu wa arc,\(∫_C \vecs F·\vecs T\, ds\); muhimu kama hiyo inaelezwa kwa suala la jumla ya Riemann, sawa na moja ya kutofautiana