15.7: Mabadiliko ya Vigezo katika Integrals nyingi
- Page ID
- 178789
- Kuamua picha ya kanda chini ya mabadiliko fulani ya vigezo.
- Compute Jacobian ya mabadiliko kutokana.
- Kutathmini muhimu mara mbili kwa kutumia mabadiliko ya vigezo.
- Kutathmini muhimu mara tatu kwa kutumia mabadiliko ya vigezo.
Kumbuka kutoka Utawala wa Kubadilisha njia ya ushirikiano na kubadilisha. Wakati wa kutathmini muhimu kama vile
\[\int_2^3 x(x^2 - 4)^5 dx, \nonumber \]
sisi badala\(u = g(x) = x^2 - 4\). Kisha\(du = 2x \, dx\) au\(x \, dx = \frac{1}{2} du\) mipaka inabadilika\(u = g(2) = 2^2 - 4 = 0\) na\(u = g(3) = 9 - 4 = 5\). Hivyo muhimu inakuwa
\[\int_0^5 \frac{1}{2}u^5 du \nonumber \]
na hii muhimu ni rahisi sana kutathmini. Kwa maneno mengine, wakati wa kutatua matatizo ya ushirikiano, tunafanya mbadala zinazofaa ili kupata muhimu ambayo inakuwa rahisi zaidi kuliko muhimu ya awali.
Sisi pia kutumika wazo hili wakati sisi kubadilishwa integrals mara mbili katika kuratibu mstatili kwa kuratibu polar na kubadilishwa integrals mara tatu katika kuratibu mstatili kwa cylindrical au spherical kuratibu kufanya hesabu rahisi. Kwa ujumla zaidi,
\[\int_a^b f(x) dx = \int_c^d f(g(u))g'(u) du, \nonumber \]
wapi\(x = g(u), \, dx = g'(u) du\), na\(u = c\) na\(u = d\) kukidhi\(c = g(a)\) na\(d = g(b)\).
Matokeo sawa hutokea katika integrals mara mbili wakati sisi mbadala
- \(x = f (r,\theta) = r \, \cos \, \theta\)
- \( y = g(r, \theta) = r \, \sin \, \theta\), na
- \(dA = dx \, dy = r \, dr \, d\theta\).
Kisha sisi kupata
\[\iint_R f(x,y) dA = \iint_S (r \, \cos \, \theta, \, r \, \sin \, \theta)r \, dr \, d\theta \nonumber \]
ambapo uwanja\(R\) ni kubadilishwa na uwanja\(S\) katika kuratibu polar. Kwa ujumla, kazi ambayo sisi kutumia mabadiliko ya vigezo kufanya ushirikiano rahisi inaitwa mabadiliko au ramani.
Mabadiliko ya Planar
Mabadiliko ya planar\(T\) ni kazi inayobadilisha kanda\(G\) katika ndege moja kuwa kanda\(R\) katika ndege nyingine kwa mabadiliko ya vigezo. Wote\(G\) na\(R\) ni subsets ya\(R^2\). Kwa mfano, Kielelezo\(\PageIndex{1}\) inaonyesha kanda\(G\) katika\(uv\) -ndege kubadilishwa katika kanda\(R\) katika\(xy\) -ndege na mabadiliko ya vigezo\(x = g(u,v)\) na\(y = h(u,v)\), au wakati mwingine sisi kuandika\(x = x(u,v)\) na\(y = y(u,v)\). Sisi kawaida kudhani kwamba kila moja ya kazi hizi ina kuendelea kwanza sehemu derivatives, ambayo ina maana\(g_u, \, g_v, \, h_u,\) na\(h_v\) kuwepo na pia ni kuendelea. Mahitaji ya mahitaji haya yatakuwa wazi hivi karibuni.
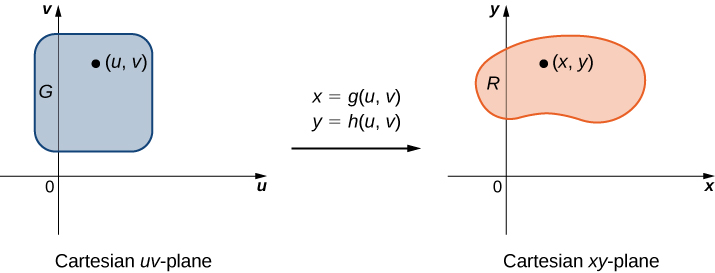
Mabadiliko\(T: \, G \rightarrow R\), hufafanuliwa kama\(T(u,v) = (x,y)\), inasemekana kuwa mabadiliko ya moja kwa moja ikiwa hakuna ramani ya pointi mbili kwenye hatua sawa ya picha.
Kuonyesha kwamba\(T\) s mabadiliko moja kwa moja, sisi kudhani\(T(u_1,v_1) = T(u_2, v_2)\) na kuonyesha kwamba kama matokeo sisi kupata\((u_1,v_1) = (u_2, v_2)\). Ikiwa mabadiliko\(T\) ni moja kwa moja katika kikoa\(G\), basi inverse\(T^{-1}\) ipo na kikoa\(R\) kama hicho\(T^{-1} \circ T\) na\(T \circ T^{-1}\) ni kazi za utambulisho.
Kielelezo\(\PageIndex{2}\) inaonyesha ramani\(T(u,v) = (x,y)\) wapi\(x\) na\(y\) ni kuhusiana\(u\) na na\(v\) kwa equations\(x = g(u,v)\) na\(y = h(u,v)\). Mkoa\(G\) ni uwanja wa\(T\) na kanda\(R\) ni mbalimbali ya\(T\), pia inajulikana kama picha ya\(G\) chini ya mabadiliko\(T\).
Tuseme mabadiliko\(T\) hufafanuliwa kama\(T(r,\theta) = (x,y)\) ambapo\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\). Pata picha ya mstatili wa polar\(G = \{(r,\theta) | 0 \leq r \leq 1, \, 0 \leq \theta \leq \pi/2\}\) katika\(r\theta\) -ndege hadi kanda\(R\) katika\(xy\) -ndege. Onyesha kwamba\(T\) ni mabadiliko moja kwa moja katika\(G\) na kupata\(T^{-1} (x,y)\).
Suluhisho
Kwa kuwa\(r\) inatofautiana kutoka 0 hadi 1 katika\(r\theta\) -ndege, tuna diski ya mviringo ya radius 0 kwa 1 katika\(xy\) -plane. Kwa sababu\(\theta\) inatofautiana kutoka 0 hadi\(\pi/2\) kwenye\(r\theta\) ndege, tunaishia kupata mduara wa robo ya radius\(1\) katika roboduara ya kwanza ya\(xy\) -plane (Kielelezo\(\PageIndex{2}\)). Hivyo\(R\) ni mduara wa robo umepakana na\(x^2 + y^2 = 1\) katika roboduara ya kwanza.
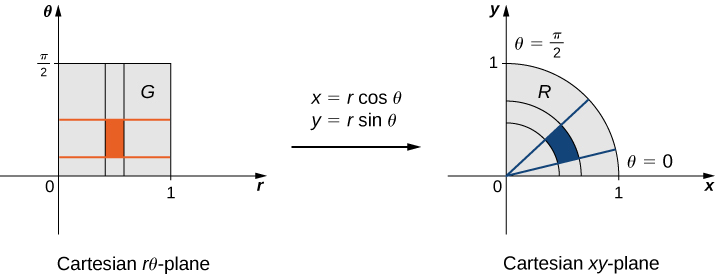
Ili kuonyesha kwamba\(T\) ni mabadiliko moja kwa moja, kudhani\(T(r_1,\theta_1) = T(r_2, \theta_2)\) na kuonyesha kama matokeo kwamba\((r_1,\theta_1) = (r_2, \theta_2)\). Katika kesi hiyo, tuna
\[T(r_1,\theta_1) = T(r_2, \theta_2), \nonumber \]
\[(x_1,y_1) = (x_1,y_1), \nonumber \]
\[(r_1 \cos \, \theta_1, r_1 \sin \, \theta_1) = (r_2 \cos \, \theta_2, r_2 \sin \, \theta_2), \nonumber \]
\[r_1 \cos \, \theta_1 = r_2 \cos \, \theta_2, \, r_1 \sin \, \theta_1 = r_2 \sin \, \theta_2. \nonumber \]
Kugawanya, tunapata
\[\frac{r_1 \cos \, \theta_1}{r_1 \sin \, \theta_1} = \frac{ r_2 \cos \, \theta_2}{ r_2 \sin \, \theta_2} \nonumber \]
\[\frac{\cos \, \theta_1}{\sin \, \theta_1} = \frac{\cos \, \theta_2}{\sin \, \theta_2} \nonumber \]
\[\tan \, \theta_1 = \tan \, \theta_2 \nonumber \]
\[\theta_1 = \theta_2 \nonumber \]
tangu kazi ya tangent ni kazi moja kwa moja katika kipindi\(0 \leq \theta \leq \pi/2\). Pia, tangu\(0 \leq r \leq 1\), tuna\(r_1 = r_2, \, \theta_1 = \theta_2\). Kwa hiyo,\((r_1,\theta_1) = (r_2, \theta_2)\) na\(T\) ni mabadiliko moja kwa moja kutoka\(G\) kwa\(R\).
Ili kupata\(T^{-1}(x,y)\) kutatua\(r,\theta\) kwa suala la\(x,y\). Tayari tunajua kwamba\(r^2 = x^2 + y^2\) na\(\tan \, \theta = \frac{y}{x}\). Hivyo\(T^{-1}(x,y) = (r,\theta)\) hufafanuliwa kama\(r = \sqrt{x^2 + y^2}\) na\(\tan^{-1} \left(\frac{y}{x}\right)\).
Hebu mabadiliko\(T\) yaelezwe na\(T(u,v) = (x,y)\) wapi\(x = u^2 - v^2\) na\(y = uv\). Pata picha ya pembetatu\(uv\) katika-ndege yenye vipeo\((0,0), \, (0,1)\), na\((1,1)\).
Suluhisho
Pembetatu na picha yake zinaonyeshwa kwenye Kielelezo\(\PageIndex{3}\). Ili kuelewa jinsi pande za pembetatu zinavyobadilika, piga upande unaojiunga\((0,0)\) na\((0,1)\) upande\(A\), upande unaojiunga\((0,0)\) na\((1,1)\) upande\(B\), na upande unaojiunga\((1,1)\) na\((0,1)\) upande\(C\).
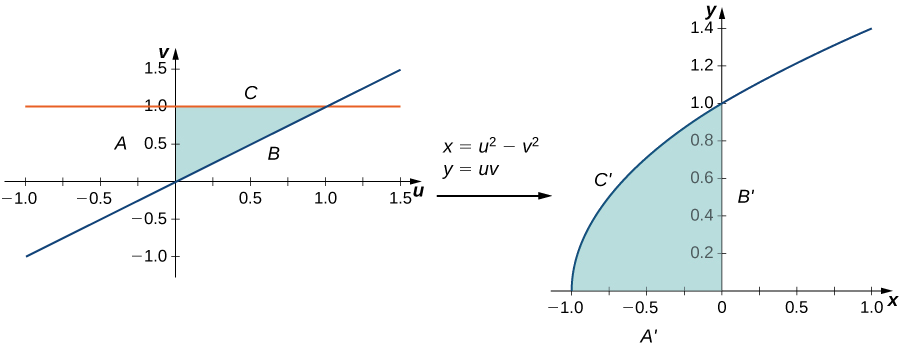
- Kwa upande\(A: \, u = 0, \, 0 \leq v \leq 1\) hubadilisha\(x = -v^2, \, y = 0\) hivyo hii ni upande\(A'\) unaojiunga\((-1,0)\) na\((0,0)\).
- Kwa upande\(B: \, u = v, \, 0 \leq u \leq 1\) hubadilisha\(x = 0, \, y = u^2\) hivyo hii ni upande\(B'\) unaojiunga\((0,0)\) na\((0,1)\).
- Kwa upande\(C: \, 0 \leq u \leq 1, \, v = 1\) inabadilisha\(x = u^2 - 1, \, y = u\) (hivyo\(x = y^2 - 1\) hivyo hii ni upande\(C'\) ambayo inafanya nusu ya juu ya safu parabolic kujiunga\((-1,0)\) na\((0,1)\).
Vipengele vyote katika kanda nzima ya pembetatu katika\(uv\) -ndege hupangwa ndani ya kanda ya parabolic katika\(xy\) -plane.
Hebu mabadiliko\(T\) kuelezwa kama\(T(u,v) = (x,y)\) ambapo\(x = u + v, \, y = 3v\). Pata picha ya mstatili\(G = \{(u,v) : \, 0 \leq u \leq 1, \, 0 \leq v \leq 2\}\) kutoka\(uv\) -ndege baada ya mabadiliko katika kanda\(R\) katika\(xy\) -ndege. Onyesha kwamba\(T\) ni mabadiliko moja kwa moja na kupata\(T^{-1} (x,y)\).
- Kidokezo
-
Fuata hatua za Mfano\(\PageIndex{1B}\).
- Jibu
-
\(T^{-1} (x,y) = (u,v)\)wapi\(u = \frac{3x-y}{3}\) na\(v = \frac{y}{3}\)
Kutumia ufafanuzi, tuna
\[\Delta A \approx J(u,v) \Delta u \Delta v = \left|\frac{\partial (x,y)}{\partial (u,v)}\right| \Delta u \Delta v. \nonumber \]
Kumbuka kuwa Jacobian mara nyingi inaashiria tu kwa
\[J(u,v) = \frac{\partial (x,y)}{\partial (u,v)}. \nonumber \]
Kumbuka pia kwamba
\[ \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \nonumber \\ \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \left( \frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\right) = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \nonumber \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} . \nonumber \]
Hivyo nukuu\(J(u,v) = \frac{\partial(x,y)}{\partial(u,v)}\) unaonyesha kwamba tunaweza kuandika uamuzi wa Jacobian na sehemu za\(x\) mstari wa kwanza na sehemu za\(y\) mstari wa pili.
Kupata Jacobian ya mabadiliko aliyopewa katika Mfano\(\PageIndex{1A}\).
Suluhisho
Mabadiliko katika mfano ni\(T(r,\theta) = ( r \, \cos \, \theta, \, r \, \sin \, \theta)\) wapi\(x = r \, \cos \, \theta\) na\(y = r \, \sin \, \theta\). Hivyo Jacobian ni
\[J(r, \theta) = \frac{\partial(x,y)}{\partial(r,\theta)} = \begin{vmatrix} \dfrac{\partial x}{\partial r} & \dfrac{\partial x}{\partial \theta} \\ \dfrac{\partial y}{\partial r} & \dfrac{\partial y}{\partial \theta} \end{vmatrix} = \begin{vmatrix} \cos \theta & -r\sin \theta \\ \sin \theta & r\cos\theta \end{vmatrix} = r \, \cos^2\theta + r \, \sin^2\theta = r ( \cos^2\theta + \sin^2\theta) = r. \nonumber \]
Kupata Jacobian ya mabadiliko aliyopewa katika Mfano\(\PageIndex{1B}\).
Suluhisho
Mabadiliko katika mfano ni\(T(u,v) = (u^2 - v^2, uv)\) wapi\(x = u^2 - v^2\) na\(y = uv\). Hivyo Jacobian ni
\[J(u,v) = \frac{\partial(x,y)}{\partial(u,v)} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} 2u & -2v \\ v & u \end{vmatrix} = 2u^2 + 2v^2. \nonumber \]
Kupata Jacobian ya mabadiliko aliyopewa katika checkpoint uliopita:\(T(u,v) = (u + v, 2v)\).
- Kidokezo
-
Fuata hatua katika mifano miwili iliyopita.
- Jibu
-
\[J(u,v) = \frac{\partial(x,y)}{\partial(u,v)} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \nonumber \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} 1 & 1 \nonumber \\ 0 & 2 \end{vmatrix} = 2 \nonumber \]
Mabadiliko ya Vigezo kwa Integrals Double
Tumeona kwamba, chini ya mabadiliko ya vigezo\(T(u,v) = (x,y)\) ambapo\(x = g(u,v)\) na\(y = h(u,v)\), kanda ndogo\(\Delta A\) katika\(xy\) -ndege ni kuhusiana na eneo lililoundwa na bidhaa\(\Delta u \Delta v\) katika\(uv\) -ndege na makadirio
\[\Delta A \approx J(u,v) \Delta u, \, \Delta v. \nonumber \]
Sasa hebu kurudi kwenye ufafanuzi wa mara mbili muhimu kwa dakika:
\[\iint_R f(x,y)fA = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}, y_{ij}) \Delta A. \nonumber \]
Akizungumzia Kielelezo\(\PageIndex{5}\), angalia kwamba tumegawanyika kanda\(S\) katika\(uv\) -plane ndani ya subrectangles ndogo\(S_{ij}\) na tunaruhusu subrectangles\(R_{ij}\) katika\(xy\) -plane kuwa picha za\(S_{ij}\) chini ya mabadiliko\(T(u,v) = (x,y)\).
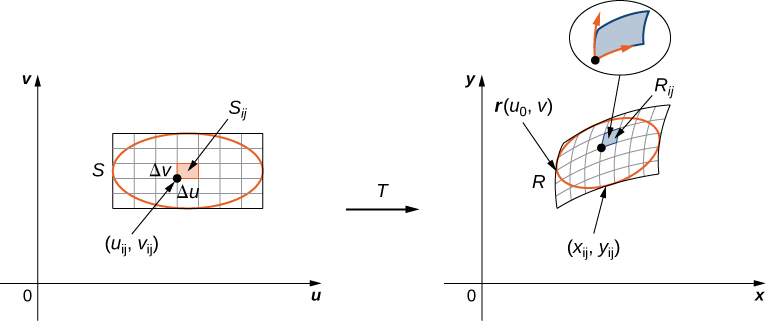
Kisha muhimu mara mbili inakuwa
\[\iint_R = f(x,y)dA = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}, y_{ij}) \Delta A = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(g(u_{ij}, v_{ij}), \, h(u_{ij}, v_{ij})) | J(u_{ij}, v_{ij})| \Delta u \Delta v. \nonumber \]
Taarifa hii ni hasa mara mbili Riemann jumla kwa muhimu
\[\iint_S f(g(u,v), \, h(u,v)) \left|\frac{\partial (x,y)}{\partial(u,v)}\right| du \, dv. \nonumber \]
Hebu\(T(u,v) = (x,y)\) wapi\(x = g(u,v)\) na\(y = h(u,v)\) kuwa\(C^1\) mabadiliko moja kwa moja, na Nonzero Jacobian juu ya mambo ya ndani ya kanda\(S\) katika\(uv\) -ndege ni ramani\(S\)\(R\) katika kanda katika\(xy\) -ndege. Ikiwa\(f\) ni kuendelea\(R\), basi
\[\iint_R f(x,y) dA = \iint_S f(g(u,v), \, h(u,v)) \left|\frac{\partial (x,y)}{\partial(u,v)}\right| du \, dv. \nonumber \]
Pamoja na theorem hii kwa integrals mara mbili, tunaweza kubadilisha vigezo kutoka\((x,y)\) kwa\((u,v)\) katika muhimu mara mbili tu kwa kuchukua nafasi
\[dA = dx \, dy = \left|\frac{\partial (x,y)}{\partial (u,v)} \right| du \, dv \nonumber \]
wakati sisi kutumia substitutions\(x = g(u,v)\)\(y = h(u,v)\) na kisha mabadiliko ya mipaka ya ushirikiano ipasavyo. Mabadiliko haya ya vigezo mara nyingi hufanya computations yoyote rahisi zaidi.
Fikiria muhimu
\[\int_0^2 \int_0^{\sqrt{2x-x^2}} \sqrt{x^2 + y^2} dy \, dx. \nonumber \]
Matumizi ya mabadiliko ya vigezo\(x = r \, \cos \, \theta\) na\(y = r \, \sin \, \theta\), na kupata muhimu kusababisha.
Suluhisho
Kwanza tunahitaji kupata eneo la ushirikiano. Mkoa huu umepakana chini\(y = 0\) na juu na\(y = \sqrt{2x - x^2}\) (Kielelezo\(\PageIndex{6}\)).
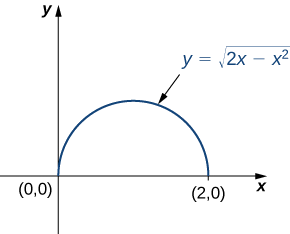
Kusambaza na kukusanya maneno, tunaona kwamba kanda ni nusu ya juu ya mduara\(x^2 + y^2 - 2x = 0\), yaani\(y^2 + ( x - 1)^2 = 1\). Katika kuratibu polar, mduara ni\(r = 2 \, cos \, \theta\) hivyo eneo la ushirikiano katika kuratibu polar imefungwa\(0 \leq r \leq \cos \, \theta\) na\(0 \leq \theta \leq \frac{\pi}{2}\).
Jacobian ni\(J(r, \theta) = r\), kama inavyoonekana katika Mfano\(\PageIndex{2A}\). tangu\(r \geq 0\), tuna\(|J(r,\theta)| = r\).
Integrand\(\sqrt{x^2 + y^2}\) mabadiliko\(r\) katika kuratibu polar, hivyo mara mbili iterated muhimu ni
\[\int_0^2 \int_0^{\sqrt{2x-x^2}} \sqrt{x^2 + y^2} dy \, dx = \int_0^{\pi/2} \int_0^{2 \, cos \, \theta} r | j(r, \theta)|dr \, d\theta = \int_0^{\pi/2} \int_0^{2 \, cos \, \theta} r^2 dr \, d\theta. \nonumber \]
Kuzingatia\(\int_0^1 \int_0^{\sqrt{1-x^2}} (x^2 + y^2) dy \, dx,\) matumizi muhimu mabadiliko ya vigezo\(x = r \, cos \, \theta\)\(y = r \, sin \, \theta\) na kupata matokeo muhimu.
- Kidokezo
-
Fuata hatua katika mfano uliopita.
- Jibu
-
\[\int_0^{\pi/2} \int_0^1 r^3 dr \, d\theta \nonumber \]
Angalia katika mfano unaofuata kwamba eneo ambalo tutaunganisha linaweza kupendekeza mabadiliko ya kufaa kwa ushirikiano. Hii ni hali ya kawaida na muhimu.
Fikiria muhimu\[\iint_R (x - y) dy \, dx, \nonumber \] ambapo\(R\) parallelogram inajiunga na pointi\((1,2), \, (3,4), \, (4,3)\), na\((6,5)\) (Kielelezo\(\PageIndex{7}\)). Kufanya mabadiliko sahihi ya vigezo, na kuandika muhimu kusababisha.
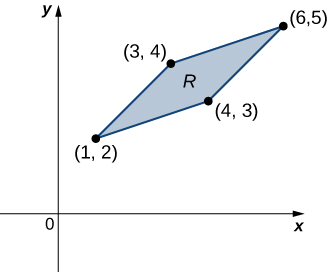
Suluhisho
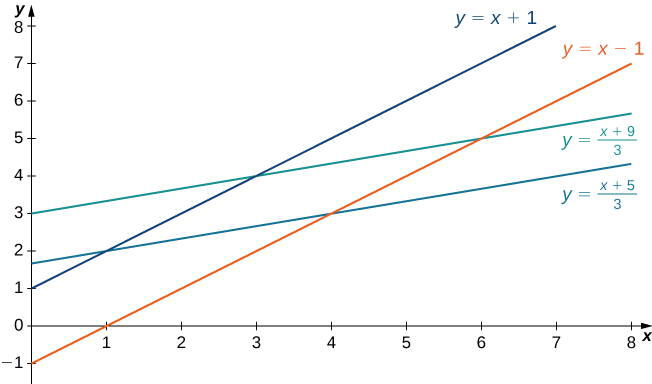
Kwanza, tunahitaji kuelewa eneo ambalo tunapaswa kuunganisha. Pande za parallelogram ni\(x - y + 1, \, x - y - 1 = 0, \, x - 3y + 5 = 0\) na\(x - 3y + 9 = 0\) (Kielelezo\(\PageIndex{8}\)). Njia nyingine ya kuwaangalia ni\(x - y = -1, \, x - y = 1, \, x - 3y = -5\), na\(x - 3y = 9\).
Wazi parallelogram imefungwa na mistari\(y = x + 1, \, y = x - 1, \, y = \frac{1}{3}(x + 5)\), na\(y = \frac{1}{3}(x + 9)\).
Kumbuka kwamba kama tungefanya\(u = x - y\) na\(v = x - 3y\), basi mipaka ya muhimu itakuwa\(-1 \leq u \leq 1\) na\(-9 \leq v \leq -5\).
Ili kutatua\(x\) na\(y\), sisi kuzidisha equation kwanza na\(3\) na Ondoa equation pili,\(3u - v = (3x - 3y) - (x - 3y) = 2x\). Kisha tuna\(x = \frac{3u-v}{2}\). Aidha, kama sisi tu Ondoa equation pili kutoka kwanza, sisi kupata\(u - v = (x - y) - (x - 3y) = 2y\) na\(y = \frac{u-v}{2}\).
Hivyo, tunaweza kuchagua mabadiliko
\[T(u,v) = \left( \frac{3u - v}{2}, \, \frac{u - v}{2} \right) \nonumber \]na kukokotoa Jacobian\(J(u,v)\). Tuna
\[J(u,v) = \frac{\partial(x,y)}{\partial(u,v)} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} 3/2 & -1/2 \nonumber \\ 1/2 & -1/2 \end{vmatrix} = -\frac{3}{4} + \frac{1}{4} = - \frac{1}{2} \nonumber \]
Kwa hiyo,\(|J(u,v)| = \frac{1}{2}\). Pia, integrand awali inakuwa
\[x - y = \frac{1}{2} [3u - v - u + v] = \frac{1}{2} [3u - u] = \frac{1}{2}[2u] = u. \nonumber \]
Kwa hiyo, kwa matumizi ya mabadiliko\(T\), mabadiliko muhimu
\[\iint_R (x - y) dy \, dx = \int_{-9}^{-5} \int_{-1}^1 J (u,v) u \, du \, dv = \int_{-9}^{-5} \int_{-1}^1\left(\frac{1}{2}\right) u \, du \, dv, \nonumber \]ambayo ni rahisi sana kukokotoa.
Kufanya mabadiliko sahihi ya vigezo katika muhimu\[\iint_R \frac{4}{(x - y)^2} dy \, dx, \nonumber \] ambapo\(R\) ni trapezoid imepakana na mistari\(x - y = 2, \, x - y = 4, \, x = 0\), na\(y = 0\). Andika muhimu inayosababisha.
- Kidokezo
-
Fuata hatua katika mfano uliopita.
- Jibu
-
\(x = \frac{1}{2}(v + u)\)na\(y = \frac{1}{2} (v - u)\)
na
\[\int_{2}^4 \int_{-u}^u \left(\frac{1}{2}\right)\cdot\frac{4}{u^2} \,dv \, du. \nonumber \]
Sisi ni tayari kutoa mkakati wa kutatua matatizo kwa ajili ya mabadiliko ya vigezo.
- Mchoro kanda iliyotolewa na tatizo katika\(xy\) ndege -na kisha kuandika milinganyo ya curves kwamba fomu ya mipaka.
- Kulingana na kanda au integrand, chagua mabadiliko\(x = g(u,v)\) na\(y = h(u,v)\).
- Kuamua mipaka mpya ya ushirikiano katika\(uv\) -ndege.
- Kupata Jacobian\(J (u,v)\).
- Katika integrand, kuchukua nafasi ya vigezo ili kupata integrand mpya.
- Badilisha nafasi\(dy \, dx\) au\(dx \, dy\), kwa namna yoyote hutokea, na\(J(u,v) du \, dv\).
Katika mfano unaofuata, tunapata badala ambayo inafanya integrand rahisi sana kukokotoa.
Kutumia mabadiliko ya vigezo\(u = x - y\) na\(v = x + y\), tathmini muhimu\[\iint_R (x - y)e^{x^2-y^2} dA, \nonumber \] ambapo\(R\) ni kanda imepakana\(x + y = 1\) na mistari na na curves\(x + y = 3\)\(x^2 - y^2 = -1\) na\(x^2 - y^2 = 1\) (tazama mkoa wa kwanza katika Kielelezo\(\PageIndex{9}\)).
Suluhisho
Kama hapo awali, kwanza kupata kanda\(R\) na picha ya mabadiliko hivyo inakuwa rahisi kupata mipaka ya ushirikiano baada ya mabadiliko kufanywa (Kielelezo\(\PageIndex{9}\)).
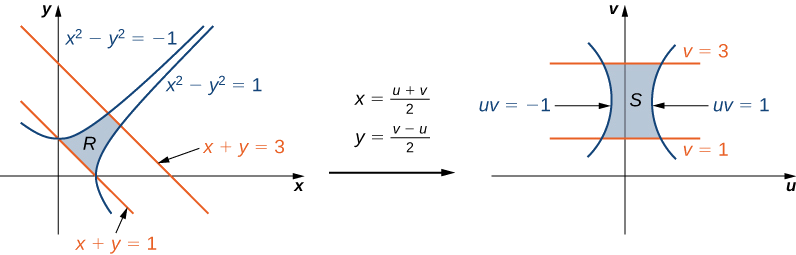
Kutokana\(u = x - y\) na\(v = x + y\), tuna\(x = \frac{u+v}{2}\)\(y = \frac{v-u}{2}\) na hivyo mabadiliko ya kutumia ni\(T(u,v) = \left(\frac{u+v}{2}, \, \frac{v-u}{2}\right)\). Mstari\(x + y = 1\) na\(x + y = 3\) kuwa\(v = 1\) na\(v = 3\), kwa mtiririko huo. Curves\(x^2 - y^2 = 1\) na\(x^2 - y^2 = -1\) kuwa\(uv = 1\) na\(uv = -1\), kwa mtiririko huo.
Hivyo tunaweza kuelezea kanda\(S\) (angalia mkoa wa pili Kielelezo\(\PageIndex{9}\)) kama
\[S = \left\{ (u,v) | 1 \leq v \leq 3, \, \frac{-1}{v} \leq u \leq \frac{1}{v}\right\}. \nonumber \]
Jacobian kwa mabadiliko haya ni
\[J(u,v) = \frac{\partial(x,y)}{\partial(u,v)} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} 1/2 & 1/2 \\ -1/2 & 1/2 \end{vmatrix} = \frac{1}{2}. \nonumber \]
Kwa hiyo, kwa kutumia mabadiliko\(T\), mabadiliko muhimu
\[\iint_R (x - y)e^{x^2-y^2} dA = \frac{1}{2} \int_1^3 \int_{-1/v}^{1/v} ue^{uv} du \, dv. \nonumber \]
Kufanya tathmini, tuna
\[\frac{1}{2} \int_1^3 \int_{-1/v}^{1/v} ue^{uv} du \, dv = \frac{2}{3e} \approx 0.245. \nonumber \]
Kutumia mbadala\(x = v\) na\(y = \sqrt{u + v}\), tathmini muhimu\(\displaystyle\iint_R y \, \sin (y^2 - x) \,dA,\) ambapo\(R\) eneo limepakana na mistari\(y = \sqrt{x}, \, x = 2\) na\(y = 0\).
- Kidokezo
-
Mchoro picha na kupata mipaka ya ushirikiano.
- Jibu
-
\(\frac{1}{2} (\sin 2 - 2)\)
Mabadiliko ya Vigezo kwa Integrals Triple
Kubadilisha vigezo katika integrals mara tatu hufanya kazi kwa njia sawa. Mbadala za kuratibu za cylindrical na spherical ni matukio maalum ya njia hii, ambayo tunaonyesha hapa.
Tuseme kwamba\(G\) ni kanda katika\(uvw\) -nafasi na ni mapped\(D\) katika\(xyz\) -nafasi (Kielelezo\(\PageIndex{10}\)) na\(C^1\) mabadiliko moja kwa moja\(T(u,v,w) = (x,y,z)\) ambapo\(x = g(u,v,w), \, y = h(u,v,w)\), na\(z = k(u,v,w)\).
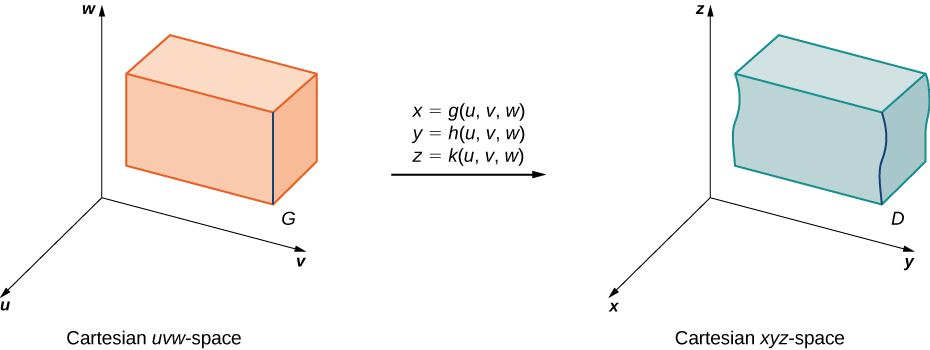
Kisha kazi yoyote\(F(x,y,z)\) defined juu\(D\) inaweza kuwa mawazo ya kama kazi nyingine\(H(u,v,w)\) ambayo hufafanuliwa juu ya\(G\):
\[F(x,y,z) = F(g(u,v,w), \, h(u,v,w), \, k(u,v,w)) = H (u,v,w). \nonumber \]
Sasa tunahitaji kufafanua Jacobian kwa vigezo vitatu.
Maamuzi ya Jacobian\(J(u,v,w)\) katika vigezo vitatu hufafanuliwa kama ifuatavyo:
\[J(u,v,w) = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} & \dfrac{\partial z}{\partial u} \\ \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} & \dfrac{\partial z}{\partial v} \\ \dfrac{\partial x}{\partial w} & \dfrac{\partial y}{\partial w} & \dfrac{\partial z}{\partial w} \end{vmatrix}. \nonumber \]
Hii pia ni sawa na
\[J(u,v,w) = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} & \dfrac{\partial x}{\partial w} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w} \\ \dfrac{\partial z}{\partial u} & \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w} \end{vmatrix}. \nonumber \]
Jacobian pia inaweza kutajwa tu kama\(\frac{\partial(x,y,z)}{\partial (u,v,w)}\).
Pamoja na mabadiliko na Jacobian kwa vigezo vitatu, tuko tayari kuanzisha theorem inayoelezea mabadiliko ya vigezo kwa integrals mara tatu.
Hebu\(T(u,v,w) = (x,y,z)\) wapi\(x = g(u,v,w), \, y = h(u,v,w)\), na\(z = k(u,v,w)\), kuwa\(C^1\) mabadiliko moja kwa moja, na Jacobian nonzero, kwamba ramani kanda\(G\) katika\(uvw\) -nafasi katika kanda\(D\) katika\(xyz\) -nafasi. Kama ilivyo katika kesi mbili-dimensional, ikiwa\(F\) inaendelea\(D\), basi
\[\begin{align} \iiint_D F(x,y,z) dV = \iiint_G f(g(u,v,w) \, h(u,v,w), \, k(u,v,w)) \left|\frac{\partial (x,y,z)}{\partial (u,v,w)}\right| du \, dv \, dw \\ = \iiint_G H(u,v,w) | J (u,v,w) | du \, dv \, dw. \end{align} \nonumber \]
Hebu sasa tuone jinsi mabadiliko katika integrals tatu kwa kuratibu cylindrical na spherical ni walioathirika na theorem hii. Tunatarajia kupata formula sawa na katika Integrals Triple katika Cylindrical na Spherical Kuratibu.
Kupata formula katika integrals mara tatu kwa
- cylindrical na
- kuratibu spherical.
Suluhisho
A.
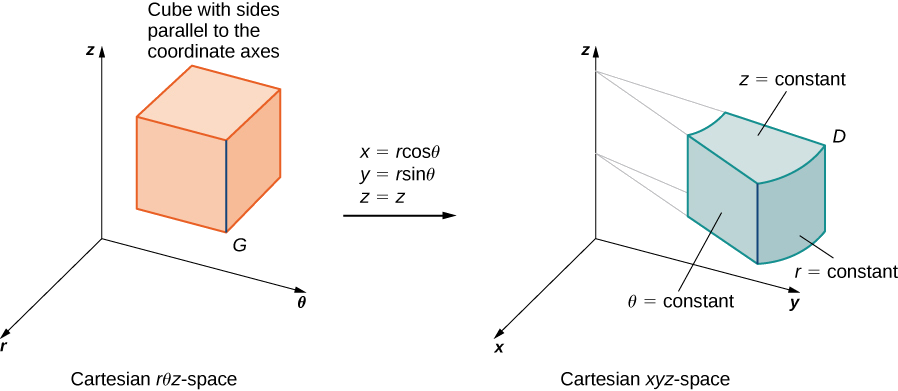
Kwa kuratibu za cylindrical, mabadiliko\(T (r, \theta, z) = (x,y,z)\) yanatoka kwenye\(r\theta z\) nafasi ya Cartesian hadi nafasi ya Cartesian\(xyz\) (Kielelezo\(\PageIndex{11}\)). Hapa\(x = r \, \cos \, \theta, \, y = r \, \sin \theta\) na\(z = z\). Jacobian kwa ajili ya mabadiliko ni
\[J(r,\theta,z) = \frac{\partial (x,y,z)}{\partial (r,\theta,z)} = \begin{vmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial z} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial z} \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial z} \end{vmatrix} \nonumber \]
\[ \begin{vmatrix} \cos \theta & -r\sin \theta & 0 \\ \sin \theta & r \cos \theta & 0 \\ 0 & 0 & 1 \end{vmatrix} = r \, \cos^2 \theta + r \, \sin^2 \theta = r. \nonumber \]
Tunajua kwamba\(r \geq 0\), hivyo\(|J(r,\theta,z)| = r\). Kisha muhimu mara tatu ni\[\iiint_D f(x,y,z)dV = \iiint_G f(r \, \cos \theta, \, r \, \sin \theta, \, z) r \, dr \, d\theta \, dz. \nonumber \]
B.
Kwa kuratibu za spherical, mabadiliko\(T(\rho,\theta,\varphi)\) yanatoka kwenye nafasi ya Cartesian hadi\(\rho\theta\varphi\) nafasi ya Cartesian\(xyz\) (Kielelezo\(\PageIndex{12}\)). Hapa\(x = \rho \, \sin \varphi \, \cos \theta, \, y = \rho \, \sin \varphi \, \sin \theta\), na\(z = \rho \, \cos \varphi\). Jacobian kwa ajili ya mabadiliko ni
\[J(\rho,\theta,\varphi) = \frac{\partial (x,y,z)}{\partial (\rho,\theta,\varphi)} = \begin{vmatrix} \frac{\partial x}{\partial \rho} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial \varphi} \\ \frac{\partial y}{\partial \rho} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial \varphi} \\ \frac{\partial z}{\partial \rho} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial \varphi} \end{vmatrix} = \begin{vmatrix} \sin \varphi \cos \theta & -\rho \sin \varphi \sin \theta & \rho \cos \varphi \cos \theta \\ \sin \varphi \sin \theta & \rho \sin \varphi \cos \theta & \rho \cos \varphi \sin \theta \\ \cos \varphi & 0 & -\rho \sin \varphi \end{vmatrix}. \nonumber \]
Kupanua uamuzi kwa heshima na mstari wa tatu:
\ [kuanza {align*} &=\ cos\ varphi\ kuanza {vMatrix} -\ rho\ dhambi\ varphi\ dhambi\ theta &\ rho\ cos\ varphi\ cos\ theta\\ rho\\ dhambi\ varphi\\ rho\ dhambi\ varphi\ kuanza {vmatrix}\ dhambi\ varphi\ cos\ theta & -\ rho\ dhambi\ varphi\ dhambi\\ dhambi\ varphi\ dhambi\ theta &\ rho\ dhambi\ varphi\ cos\ theta\ mwisho {vMatrix}\\ [4pt]
&=\ cos\ varphi (-\ rho ^ 2\ dhambi\ varphi\,\ cos\ varphi\,\ dhambi\ varphi\\,\ cos ^ 2\ theta)\\ &\ quad -\ rho\ dhambi\ varphi (\ rho\ dhambi ^ 2\ varphi\ cos ^ 2\ theta +\ rho\ dhambi ^ 2\ varphi\ dhambi ^ 2\ theta)\\ [4pt]
&=-\ rho ^ 2\ dhambi\ varphi\ cos ^ 2\ varphi (\ dhambi ^ 2\ theta +\ cos ^ 2\ theta) -\ rhos ^ 2\ dhambi\ varphi 2\ varphi (\ dhambi ^ 2\ theta +\ cos ^ 2\ theta)\\ [4pt]
&= -\ rho^2\ dhambi\ varphi\ cos^2\ varphi -\ rho ^ 2\ dhambi\ varphi\ dhambi ^ 2\ varphi\\ [4pt]
&= -\ rho \ dhambi\ varphi (\ cos ^ 2\ varphi +\ dhambi ^ 2\ varphi) = -\ rho ^ 2\ dhambi\ varphi. \ mwisho {align*}\]
Tangu\(0 \leq \varphi \leq \pi\), ni lazima tuwe na\(\sin \varphi \geq 0\). Hivyo\(|J(\rho,\theta, \varphi)| = |-\rho^2 \sin \varphi| = \rho^2 \sin \varphi.\)
.png)
Kisha muhimu mara tatu inakuwa
\[\iiint_D f(x,y,z) dV = \iiint_G f(\rho \, \sin \varphi \, \cos \theta, \, \rho \, \sin \varphi \, \sin \theta, \rho \, \cos \varphi) \rho^2 \sin \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
Hebu jaribu mfano mwingine na ubadilishaji tofauti.
Tathmini muhimu mara tatu
\[\int_0^3 \int_0^4 \int_{y/2}^{(y/2)+1} \left(x + \frac{z}{3}\right) dx \, dy \, dz \nonumber \]
Katika\(xyz\) -nafasi kwa kutumia mabadiliko
\(u = (2x - y) /2, \, v = y/2\), na\(w = z/3\).
Kisha kuunganisha juu ya mkoa sahihi katika\(uvw\) -nafasi.
Suluhisho
Kama hapo awali, aina fulani ya mchoro wa kanda\(G\) katika\(xyz\) -nafasi juu ya ambayo tunapaswa kufanya ushirikiano inaweza kusaidia kutambua kanda\(D\) katika\(uvw\) -space (Kielelezo\(\PageIndex{13}\)). Wazi\(G\) katika\(xyz\) -nafasi imepakana na ndege\(x = y/2, \, x = (y/2) + 1, \, y = 0, \, y = 4, \, z = 0\), na\(z = 4\). Tunajua pia kwamba tunapaswa kutumia\(u = (2x - y) /2, \, v = y/2\), na\(w = z/3\) kwa mabadiliko. Tunahitaji kutatua\(x,y\) na\(z\). Hapa tunaona kwamba\(x = u + v, \, y = 2v\), na\(z = 3w\).
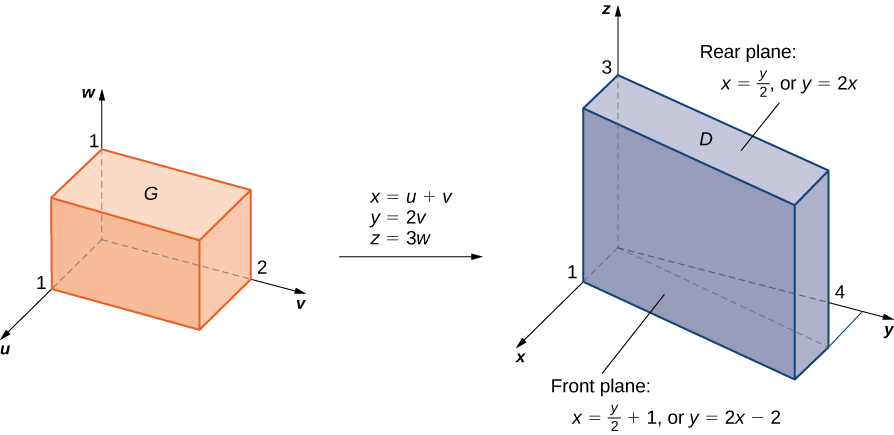
Kutumia algebra ya msingi, tunaweza kupata nyuso zinazofanana kwa kanda\(G\) na mipaka ya ushirikiano katika\(uvw\) -nafasi. Ni rahisi kuorodhesha equations hizi katika meza.
| Ulinganifu katika\(xyz\) kwa kanda\(D\) | Equations sambamba katika\(uvw\) kwa ajili ya kanda\(G\) | Mipaka kwa ajili ya ushirikiano katika\(uvw\) |
|---|---|---|
| \ (xyz\) kwa kanda\(D\) "style="wima align:katikati;" >\(x = y/2\) | \ (uvw\) kwa kanda\(G\) "style="vertical-align:katikati;" >\(u + v = 2v/2 = v\) | \ (uvw\)” style="wima align:katikati; ">\(u = 0\) |
| \ (xyz\) kwa kanda\(D\) "style="wima align:katikati;" >\(x = y/2\) | \ (uvw\) kwa kanda\(G\) "style="vertical-align:katikati;" >\(u + v = (2v/2) + 1 = v + 1\) | \ (uvw\)” style="wima align:katikati; ">\(u = 1\) |
| \ (xyz\) kwa kanda\(D\) "style="wima align:katikati;" >\(y = 0\) | \ (uvw\) kwa kanda\(G\) "style="vertical-align:katikati;" >\(2v = 0\) | \ (uvw\)” style="wima align:katikati; ">\(v = 0\) |
| \ (xyz\) kwa kanda\(D\) "style="wima align:katikati;" >\(y = 4\) | \ (uvw\) kwa kanda\(G\) "style="vertical-align:katikati;" >\(2v = 4\) | \ (uvw\)” style="wima align:katikati; ">\(v = 2\) |
| \ (xyz\) kwa kanda\(D\) "style="wima align:katikati;" >\(z = 0\) | \ (uvw\) kwa kanda\(G\) "style="vertical-align:katikati;" >\(3w = 0\) | \ (uvw\)” style="wima align:katikati; ">\(w = 0\) |
| \ (xyz\) kwa kanda\(D\) "style="wima align:katikati;" >\(z = 3\) | \ (uvw\) kwa kanda\(G\) "style="vertical-align:katikati;" >\(3w = 3\) | \ (uvw\)” style="wima align:katikati; ">\(w = 1\) |
Sasa tunaweza kuhesabu Jacobian kwa mabadiliko:
\[J(u,v,w) = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} & \dfrac{\partial x}{\partial w} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w} \\ \dfrac{\partial z}{\partial u} & \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w} \end{vmatrix} = \begin{vmatrix} 1 & 1 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{vmatrix} = 6. \nonumber \]
Kazi ya kuunganishwa inakuwa
\[f(x,y,z) = x + \frac{z}{3} = u + v + \frac{3w}{3} = u + v + w. \nonumber \]
Sasa tuko tayari kuweka kila kitu pamoja na kukamilisha tatizo.
\ [kuanza {align*}\ int_0 ^ 3\ int_0 ^ 4\ int_ {y/2} ^ {(y/2) +1}\ kushoto (x +\ frac {z} {3}\ haki) dx\, dy\, dz &=\ int_0 ^ 1\ int_0 ^ 2\ int_0 ^ 1 (u + v + w) |J (u, v, w) |du\, dv\, dw\\ [4pt]
&=\ int_0 ^ 1\ int_0 ^ 2\ int_0 ^ 1 (u + v + w) |6|du\, dv\\ [4pt]
&= 6\ int_0 ^ 1\ int_0 ^ 2\ int_ 0 ^ 1 (u + v + w)\, du\, dv\, dw\\ [4pt]
&= 6\ int_0 ^ 1\ int_0 ^ 2\ kushoto [\ frac {u ^ 2} {2} + vu + wu\ haki] _0 ^ 1\, dv\\, dw\\ [4pt]
&= 6\ int_0 ^ 1\ int_0_0 ^ 2\ kushoto (\ frac {1} {2} + v + u\ haki) dv\, dw\\ [4pt]
&= 6\ int_0 ^ 1\ kushoto [\ frac {1} {2} v +\ Frac {v ^ 2} {2} +\ frac {v ^ 2} + wv\ haki] _0 ^ 2 dw\\ [4pt]
&= 6\ int_0 ^ 1 (3 + 2w)\, dw = 6\ Big [3w + w ^ 2\ Big] _0 ^ 1 = 24. \ mwisho {align*}\]
Hebu\(D\) kuwa kanda katika\(xyz\) -nafasi inavyoelezwa na\(1 \leq x \leq 2, \, 0 \leq xy \leq 2\), na\(0 \leq z \leq 1\).
Tathmini\(\iiint_D (x^2 y + 3xyz) \, dx \, dy \, dz\) kwa kutumia mabadiliko\(u = x, \, v = xy\), na\(w = 3z\).
- Kidokezo
-
Fanya meza kwa kila uso wa mikoa na uamuzi juu ya mipaka, kama inavyoonekana katika mfano.
- Jibu
-
\[\int_0^3 \int_0^2 \int_1^2 \left(\frac{v}{3} + \frac{vw}{3u}\right) du \, dv \, dw = 2 + \ln 8 \nonumber \]
Dhana muhimu
- Mabadiliko\(T\) ni kazi inayobadilisha kanda\(G\) katika ndege moja (nafasi) kuwa\(R\) kanda. katika ndege nyingine (nafasi) kwa mabadiliko ya vigezo.
- Mabadiliko\(T: G \rightarrow R\) hufafanuliwa kama\(T(u,v) = (x,y)\) (au\(T(u,v,w) = (x,y,z))\) inasemekana kuwa mabadiliko ya moja kwa moja ikiwa hakuna ramani mbili kwenye ramani sawa ya picha.
- Ikiwa\(f\) ni kuendelea\(R\), basi\[\iint_R f(x,y) dA = \iint_S f(g(u,v), \, h(u,v)) \left|\frac{\partial(x,y)}{\partial (u,v)}\right| du \, dv. \nonumber \]
- Ikiwa\(F\) ni kuendelea\(R\), basi\[\begin{align*}\iiint_R F(x,y,z) \, dV &= \iiint_G F(g(u,v,w), \, h(u,v,w), \, k(u,v,w) \left|\frac{\partial(x,y,z)}{\partial (u,v,w)}\right| \,du \, dv \, dw \\[4pt] &= \iiint_G H(u,v,w) |J(u,v,w)| \, du \, dv \, dw. \end{align*}\]
[T] Lamé ovals (au superellipses) ni curves ndege ya\(\left(\frac{x}{a}\right)^n + \left( \frac{y}{b}\right)^n = 1\) milinganyo, ambapo a, b, na n ni chanya namba halisi.
Matumizi CAS kwa graph mikoa\(R\) imepakana na Lamé ovals kwa\(a = 1, \, b = 2, \, n = 4\)\(n = 6\) mtiririko huo.
pata mabadiliko ambayo ramani eneo\(R\) imepakana na mviringo Lamé\(x^4 + y^4 = 1\) pia inaitwa squircle na graphed katika takwimu zifuatazo, katika kitengo disk.
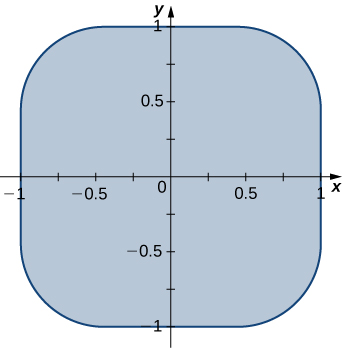
c Tumia CAS ili kupata makadirio ya eneo hilo\(A (R)\) of the region \(R\) bounded by \(x^4 + y^4 = 1\). Round your answer to two decimal places.
[T] Lamé ovals have been consistently used by designers and architects. For instance, Gerald Robinson, a Canadian architect, has designed a parking garage in a shopping center in Peterborough, Ontario, in the shape of a superellipse of the equation \(\left(\frac{x}{a}\right)^n + \left( \frac{y}{b}\right)^n = 1\) with \(\frac{a}{b} = \frac{9}{7}\) and \(n = e\). Use a CAS to find an approximation of the area of the parking garage in the case \(a = 900\) yards, \(b = 700\) yards, and \(n = 2.72\) yards.
[Hide Solution]
\(A(R) \simeq 83,999.2\)
Chapter Review Exercises
True or False? Justify your answer with a proof or a counterexample.
\[\int_a^b \int_c^d f(x,y) \, dy \, dx = \int_c^d \int_a^b f(x,y) \, dy \, dx \nonumber \]
Fubini’s theorem can be extended to three dimensions, as long as \(f\) is continuous in all variables.
[Hide solution]
True.
The integral \[\int_0^{2\pi} \int_0^1 \int_0^1 dz \, dr \, d\theta \nonumber \] represents the volume of a right cone.
The Jacobian of the transformation for \(x = u^2 - 2v, \, y = 3v - 2uv\) is given by \(-4u^2 + 6u + 4v\).
[Hide Solution]
False.
Evaluate the following integrals.
\[\iint_R (5x^3y^2 - y^2) \, dA, \, R = \{(x,y)|0 \leq x \leq 2, \, 1 \leq y \leq 4\} \nonumber \]
\[\iint_D \frac{y}{3x^2 + 1} dA, \, D = \{(x,y) |0 \leq x \leq 1, \, -x \leq y \leq x\} \nonumber \]
[Hide Solution]
\(0\)
\[\iint_D \sin (x^2 + y^2) dA \nonumber \] where \(D\) is a disk of radius \(2\) centered at the origin \[\int_0^1 \int_0^1 xye^{x^2} dx \, dy \nonumber \]
[Hide Solution]
\(\frac{1}{4}\)
\[\int_{-1}^1 \int_0^z \int_0^{x-z} 6dy \, dx \, dz \nonumber \]
\[\iiint_R 3y \, dV, \nonumber \] where \(R = \{(x,y,z) |0 \leq x \leq 1, \, 0 \leq y \leq x, \, 0 \leq z \leq \sqrt{9 - y^2}\}\)
[Hide Solution]
\(1.475\)
\[\int_0^2 \int_0^{2\pi} \int_r^1 r \, dz \, d\theta \, dr \nonumber \]
\[\int_0^{2\pi} \int_0^{\pi/2} \int_1^3 \rho^2 \, \sin(\varphi) d\rho \, d\varphi, \, d\theta \nonumber \]
[Hide Solution]
\(\frac{52}{3} \pi\)
\[\int_0^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \int_{-\sqrt{1-x^2-y^2}}^{\sqrt{1-x^2-y^2}} dz \, dy \, sx \nonumber \]
For the following problems, find the specified area or volume.
The area of region enclosed by one petal of \(r = \cos (4\theta)\).
[Hide Solution]
\(\frac{\pi}{16}\)
The volume of the solid that lies between the paraboloid \(z = 2x^2 + 2y^2\) and the plane \(z = 8\).
The volume of the solid bounded by the cylinder \(x^2 + y^2 = 16\) and from \(z = 1\) to \(z + x = 2\).
[Hide Solution]
\(93.291\)
The volume of the intersection between two spheres of radius 1, the top whose center is \((0,0,0.25)\) and the bottom, which is centered at \((0,0,0)\).
For the following problems, find the center of mass of the region.
\(\rho(x,y) = xy\) on the circle with radius \(1\) in the first quadrant only.
[Hide Solution]
\(\left(\frac{8}{15}, \frac{8}{15}\right)\)
\(\rho(x,y) = (y + 1) \sqrt{x}\) in the region bounded by \(y = e^x, \, y = 0\), and \(x = 1\).
\(\rho(x,y,z) = z\) on the inverted cone with radius \(2\) and height \(2\).
\(\left(0,0,\frac{8}{5}\right)\)
The volume an ice cream cone that is given by the solid above \(z = \sqrt{(x^2 + y^2)}\) and below \(z^2 + x^2 + y^2 = z\).
The following problems examine Mount Holly in the state of Michigan. Mount Holly is a landfill that was converted into a ski resort. The shape of Mount Holly can be approximated by a right circular cone of height \(1100\) ft and radius \(6000\) ft.
If the compacted trash used to build Mount Holly on average has a density \(400 \, lb/ft^3\), find the amount of work required to build the mountain.
[Hide Solution]
\(1.452 \pi \times 10^{15} \) ft-lb
In reality, it is very likely that the trash at the bottom of Mount Holly has become more compacted with all the weight of the above trash. Consider a density function with respect to height: the density at the top of the mountain is still density \(400 \, lb/ft^3\) and the density increases. Every \(100\) feet deeper, the density doubles. What is the total weight of Mount Holly?
The following problems consider the temperature and density of Earth’s layers.
[T] The temperature of Earth’s layers is exhibited in the table below. Use your calculator to fit a polynomial of degree \(3\) to the temperature along the radius of the Earth. Then find the average temperature of Earth. (Hint: begin at \(0\) in the inner core and increase outward toward the surface)
| Layer | Depth from center (km) | Temperature \(^oC\) |
| Rocky Crust | 0 to 40 | 0 |
| Upper Mantle | 40 to 150 | 870 |
| Mantle | 400 to 650 | 870 |
| Inner Mantel | 650 to 2700 | 870 |
| Molten Outer Core | 2890 to 5150 | 4300 |
| Inner Core | 5150 to 6378 | 7200 |
Source: http://www.enchantedlearning.com/sub...h/Inside.shtml
[Hide Solution]
\(y = -1.238 \times 10^{-7} x^3 + 0.001196 x^2 - 3.666x + 7208\); average temperature approximately \(2800 ^oC\)
[T] The density of Earth’s layers is displayed in the table below. Using your calculator or a computer program, find the best-fit quadratic equation to the density. Using this equation, find the total mass of Earth.
| Layer | Depth from center (km) | Density \((g/cm^3)\) |
| Inner Core | 0 | 12.95 |
| Outer Core | 1228 | 11.05 |
| Mantle | 3488 | 5.00 |
| Upper Mantle | 6338 | 3.90 |
| Crust | 6378 | 2.55 |
Source: http://hyperphysics.phy-astr.gsu.edu...rthstruct.html
The following problems concern the Theorem of Pappus (see Moments and Centers of Mass for a refresher), a method for calculating volume using centroids. Assuming a region \(R\), when you revolve around the \(x\)-axis the volume is given by \(V_x = 2\pi A \bar{y}\), and when you revolve around the \(y\)-axis the volume is given by \(V_y = 2\pi A \bar{x}\), where \(A\) is the area of \(R\). Consider the region bounded by \(x^2 + y^2 = 1\) and above \(y = x + 1\).
Find the volume when you revolve the region around the \(x\)-axis.
[Hide Solution]
\(\frac{\pi}{3}\)
Find the volume when you revolve the region around the \(y\)-axis.
Glossary
- Jacobian
-
the Jacobian \(J (u,v)\) in two variables is a \(2 \times 2\) determinant:
\[J(u,v) = \begin{vmatrix} \frac{\partial x}{\partial u} \frac{\partial y}{\partial u} \nonumber \\ \frac{\partial x}{\partial v} \frac{\partial y}{\partial v} \end{vmatrix}; \nonumber \]
the Jacobian \(J (u,v,w)\) in three variables is a \(3 \times 3\) determinant:
\[J(u,v,w) = \begin{vmatrix} \frac{\partial x}{\partial u} \frac{\partial y}{\partial u} \frac{\partial z}{\partial u} \nonumber \\ \frac{\partial x}{\partial v} \frac{\partial y}{\partial v} \frac{\partial z}{\partial v} \nonumber \\ \frac{\partial x}{\partial w} \frac{\partial y}{\partial w} \frac{\partial z}{\partial w}\end{vmatrix} \nonumber \]
- one-to-one transformation
- a transformation \(T : G \rightarrow R\) defined as \(T(u,v) = (x,y)\) is said to be one-to-one if no two points map to the same image point
- planar transformation
- a function \(T\) that transforms a region \(G\) in one plane into a region \(R\) in another plane by a change of variables
- transformation
- a function that transforms a region GG in one plane into a region RR in another plane by a change of variables



Wajacobia
Kumbuka kwamba tulielezea karibu na mwanzo wa sehemu hii kwamba kila kazi ya sehemu lazima iwe na derivatives ya kwanza ya sehemu, ambayo ina maana kwamba\(g_u, g_v, h_u\) na\(h_v\) kuwepo na pia inaendelea. Mabadiliko ambayo ina mali hii inaitwa\(C^1\) mabadiliko (hapa\(C\) inaashiria kuendelea). Hebu\(T(u,v) = (g(u,v), \, h(u,v))\), wapi\(x = g(u,v)\) na\(y = h(u,v)\) uwe\(C^1\) mabadiliko ya moja kwa moja. Tunataka kuona jinsi inabadilisha vitengo vidogo\(S, \, \Delta u\) vya mkoa wa mstatili na\(\Delta v\) vitengo, katika\(uv\) -ndege (Kielelezo\(\PageIndex{4}\)).
Tangu\(x = g(u,v)\) na\(y = h(u,v)\), tuna vector nafasi\(r(u,v) = g(u,v)i + h(u,v)j\) ya picha ya uhakika\((u,v)\). Tuseme kwamba\((u_0,v_0)\) ni kuratibu ya uhakika katika kona ya chini kushoto kwamba mapped kwa\((x_0,y_0) = T(u_0,v_0)\)\(v = v_0\) ramani line Curve picha na kazi vector\(r(u,v_0)\), na vector tangent katika\((x_0,y_0)\) Curve picha ni
\[r_u = g_u (u_0,v_0)i + h_v (u_0,v_0)j = \frac{\partial x}{\partial u}i + \frac{\partial y}{\partial u}j. \nonumber \]
Vile vile,\(u = u_0\) ramani za mstari kwenye safu ya picha na kazi ya vector\(r(u_0,v)\), na vector ya tangent\((x_0,y_0)\) kwenye pembe ya picha ni
\[r_v = g_v (u_0,v_0)i + h_u (u_0,v_0)j = \frac{\partial x}{\partial v}i + \frac{\partial y}{\partial v}j. \nonumber \]
Sasa, kumbuka kuwa
\[r_u = \lim_{\Delta u \rightarrow 0} \frac{r (u_0 + \Delta u, v_0) - r ( u_0,v_0)}{\Delta u}\, so \, r (u_0 + \Delta u,v_0) - r(u_0,v_0) \approx \Delta u r_u. \nonumber \]
Vile vile,
\[r_v = \lim_{\Delta v \rightarrow 0} \frac{r (u_0,v_0 + \Delta v) - r ( u_0,v_0)}{\Delta v}\, so \, r (u_0,v_0 + \Delta v) - r(u_0,v_0) \approx \Delta v r_v. \nonumber \]
Hii inaruhusu sisi kukadiria eneo\(\Delta A\) la picha\(R\) kwa kutafuta eneo la parallelogram iliyoundwa\(\Delta vr_v\) na pande na\(\Delta ur_u\). Kwa kutumia bidhaa msalaba wa wadudu hawa wawili kwa kuongeza k th sehemu kama\(0\), eneo\(\Delta A\) la picha\(R\) (rejea Msalaba Bidhaa) ni takriban\(|\Delta ur_u \times \Delta v r_v| = |r_u \times r_v|\Delta u \Delta v\). Katika fomu ya kuamua, bidhaa ya msalaba ni
\[r_u \times r_v = \begin{vmatrix} i & j & k \\ \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} & 0 \\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} & 0 \end{vmatrix} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \\ \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix} k = \left(\frac{\partial x}{\partial u} \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\right)k \nonumber \]
Tangu\(|k| = 1,\) tuna
\(\Delta A \approx |r_u \times r_v| \Delta u \Delta v = \left( \frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\right) \Delta u \Delta v.\)
ufafanuzi: Jacobian
Jacobian ya\(C^1\) mabadiliko\(T(u,v) = (g(u,v), \, h(u,v))\) inaashiria\(J(u,v)\) na inaelezwa na\(2 \times 2\) kuamua
\[J(u,v) = \left|\frac{\partial (x,y)}{\partial (u,v)} \right| = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \\ \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \left( \frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\right). \nonumber \]