15.4: Integrals Triple

Malengo ya kujifunza

• Kutambua wakati kazi ya vigezo tatu ni integrable juu ya sanduku mstatili.
• Tathmini muhimu mara tatu kwa kuelezea kama muhimu iterated.
• Kutambua wakati kazi ya vigezo tatu ni integrable juu ya kanda imefungwa na imepakana.
• Kurahisisha hesabu kwa kubadilisha utaratibu wa ushirikiano wa tatu muhimu.
• Tumia thamani ya wastani ya kazi ya vigezo vitatu.

Hapo awali, tulijadili muhimu mara mbili ya kazi$f(x,y)$ ya vigezo viwili juu ya mkoa wa mstatili katika ndege. Katika sehemu hii sisi kufafanua muhimu mara tatu ya kazi$f(x,y,z)$ ya vigezo tatu juu ya mstatili sanduku imara katika nafasi,$\mathbb{R}^3$. Baadaye katika sehemu hii tunapanua ufafanuzi kwa mikoa zaidi ya jumla$\mathbb{R}^3$.

Kazi Integrable ya Vigezo Tatu

Tunaweza kufafanua sanduku mstatili$B$ katika$\mathbb{R}^3$ kama

$$B = \big\{(x,y,z)\,|\,a \leq x \leq b, \, c \leq y \leq d, \, e \leq z \leq f \big\}. \nonumber$$

Tunafuata utaratibu sawa na kile tulichofanya hapo awali. Tunagawanya muda$[a,b]$ katika$l$ sehemu ndogo$[x_{i-1},x_i]$ za urefu sawa$\Delta x$ na

$$\Delta x = \dfrac{x_i - x_{i-1}}{l}, \nonumber$$

kugawanya muda$[c,d]$ katika$m$ sehemu ndogo$[y_{i-1}, y_i]$ za urefu sawa$\Delta y$ na

$$\Delta y = \dfrac{y_j - y_{j-1}}{m}, \nonumber$$

na ugawanye muda$[e,f]$ katika$n$ sehemu ndogo$[z_{i-1},z_i]$ za urefu sawa$\Delta z$ na

$$\Delta z = \dfrac{z_k - z_{k-1}}{n} \nonumber$$

Kisha sanduku la mstatili$B$ linagawanywa katika$lmn$ vifungu vidogo:

$$B_{ijk} = [x_{i-1}, x_i] \times [y_{i-1}, y_i] \times [z_{i-1},z_i], \nonumber$$

kama inavyoonekana katika Kielelezo$\PageIndex{1}$.

Kielelezo$\PageIndex{1}$: sanduku mstatili$\mathbb{R}^3$ imegawanywa katika subboxes na ndege sambamba na ndege kuratibu.

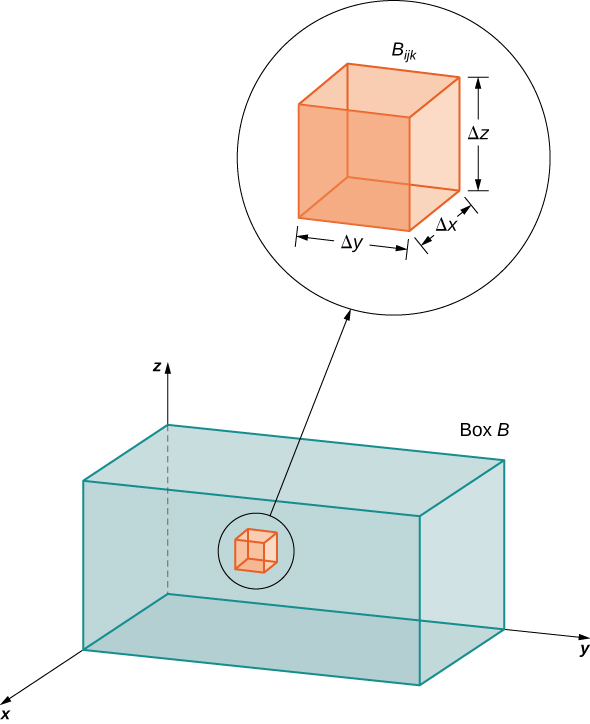
Kwa kila$i, \, j,$ na$k$, fikiria hatua ya sampuli$(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)$ katika kila sanduku ndogo$B_{ijk}$. Tunaona kwamba kiasi chake ni$\Delta V = \Delta x \Delta y \Delta z$. Fomu tatu Riemann jumla

$$\sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\,\Delta x \Delta y \Delta z. \nonumber$$

Sisi kufafanua muhimu mara tatu katika suala la kikomo cha mara tatu Riemann jumla, kama tulivyofanya kwa muhimu mara mbili katika suala la mara mbili Riemann jumla.

Ufafanuzi: muhimu mara tatu

Muhimu wa tatu wa kazi$f(x,y,z)$ juu ya sanduku la mstatili$B$ hufafanuliwa kama

$$\lim_{l,m,n\rightarrow\infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber$$ kama kikomo hii ipo.

Wakati muhimu mara tatu ipo$B$ kwenye kazi$f(x,y,z)$ inasemekana kuwa integrable juu ya$B$. Pia, muhimu mara tatu ipo ikiwa$f(x,y,z)$ inaendelea$B$. Kwa hiyo, tutatumia kazi zinazoendelea kwa mifano yetu. Hata hivyo, mwendelezo ni wa kutosha lakini si lazima; kwa maneno mengine,$f$ imepakana$B$ na kuendelea isipokuwa pengine kwenye mipaka ya$B$. Hatua ya sampuli$(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)$ inaweza kuwa hatua yoyote katika sanduku ndogo ya mstatili$B_{ijk}$ na mali zote za muhimu mbili zinatumika kwa sehemu tatu. Kama vile muhimu mara mbili ina maombi mengi ya vitendo, muhimu mara tatu pia ina maombi mengi, ambayo sisi kujadili katika sehemu ya baadaye.

Sasa kwa kuwa tumeanzisha dhana ya tatu muhimu, tunahitaji kujua jinsi ya kuihesabu. Kama vile katika kesi ya muhimu mara mbili, tunaweza kuwa na iterated mara tatu muhimu, na hivyo, toleo la theorem Fubini kwa integrals mara tatu ipo.

Theorem ya Fubini kwa Integrals Triple

Ikiwa$f(x,y,z)$ ni kuendelea kwenye sanduku la mstatili$B = [a,b] \times [c,d] \times [e,f]$, basi

$$\iint_B f(x,y,z) \,dV = \int_e^f \int_c^d \int_a^b f(x,y,z) \,dx \, dy \, dz. \nonumber$$

Hii muhimu pia ni sawa na yoyote ya nyingine tano orderings inawezekana kwa iterated mara tatu muhimu.

Kwa$a, b, c, d, e$ na idadi$f$ halisi, iterated tatu muhimu inaweza walionyesha katika amri sita tofauti:

$$\begin{align} \int_e^f \int_c^d \int_a^b f(x,y,z)\, dx \, dy \, dz = \int_e^f \left( \int_c^d \left( \int_a^b f(x,y,z) \,dx \right) dy \right) dz \\ = \int_c^d \left( \int_e^f \left( \int_a^b f(x,y,z) \,dx \right)dz \right) dy \\ = \int_a^b \left( \int_e^f \left( \int_c^d f(x,y,z) \,dy \right)dz \right) dx \\ = \int_e^f \left( \int_a^b \left( \int_c^d f(x,y,z) \,dy \right) dx \right) dz \\ = \int_c^d \left( \int_a^b \left( \int_c^d f(x,y,z) \,dz\right)dx \right) dy \\ = \int_a^b \left( \int_c^d \left( \int_e^f f(x,y,z) \,dz \right) dy \right) dx \end{align} \nonumber$$

Kwa sanduku la mstatili, utaratibu wa ushirikiano haufanyi tofauti yoyote muhimu katika kiwango cha ugumu katika hesabu. Sisi kukokotoa integrals mara tatu kwa kutumia Theorem Fubini badala ya kutumia Riemann jumla ufafanuzi. Tunafuata utaratibu wa ushirikiano kwa njia sawa na tulivyofanya kwa integrals mbili (yaani, kutoka ndani na nje).

Mfano$\PageIndex{1}$: Evaluating a Triple Integral

Tathmini muhimu mara tatu $$\int_{z=0}^{z=1} \int_{y=2}^{y=4} \int_{x=-1}^{x=5} (x + yz^2)\, dx \, dy \, dz. \nonumber$$

Suluhisho

Utaratibu wa ushirikiano umeelezwa katika tatizo, hivyo kuunganisha kwa heshima ya$x$ kwanza, kisha y, na kisha$z$.

$$\begin{align*}&\int_{z=0}^{z=1} \int_{y=2}^{y=4} \int_{x=-1}^{x=5} (x + yz^2) \,dx \,dy \,dz \\ &= \int_{z=0}^{z=1} \int_{y=2}^{y=4} \left. \left[ \dfrac{x^2}{2} + xyz^2\right|_{x=-1}^{x=5}\right]\,dy \,dz &&\text{Integrate with respect to $x$.}\\ &= \int_{z=0}^{z=1} \int_{y=2}^{y=4} \left[12+6yz^2\right] \,dy \,dz &&\text{Evaluate.}\\ &= \int_{z=0}^{z=1} \left[ \left.12y+6\dfrac{y^2}{2}z^2 \right|_{y=2}^{y=4} \right] dz &&\text{Integrate with respect to $y$.} \\ &= \int_{z=0}^{z=1} [24+36z^2] \, dz &&\text{Evaluate.} \\ &= \left[ 24z+36\dfrac{z^3}{3} \right]_{z=0}^{z=1} &&\text{Integrate with respect to $z$.}\\ &=36. &&\text{Evaluate.}\end{align*}$$

Mfano$\PageIndex{2}$: Evaluating a Triple Integral

Tathmini muhimu mara tatu

$$\iiint_B x^2 yz \,dV \nonumber$$

ambapo$B = \big\{(x,y,z)\,|\, - 2 \leq x \leq 1, \, 0 \leq y \leq 3, \, 1 \leq z \leq 5 \big\}$ kama inavyoonekana katika Kielelezo$\PageIndex{2}$.

Kielelezo$\PageIndex{2}$: Kutathmini muhimu mara tatu juu ya sanduku lililopewa mstatili.

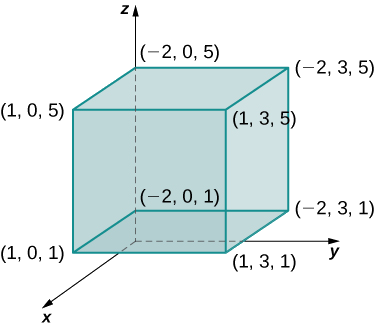
Suluhisho

Utaratibu haujainishwa, lakini tunaweza kutumia muhimu ya iterated kwa utaratibu wowote bila kubadilisha kiwango cha ugumu. Chagua, sema, kuunganisha$y$ kwanza, kisha$x$, na kisha$z$.

$$\begin{align*}\iiint\limits_{B} x^2 yz \,dV &= \int_1^5 \int_{-2}^1 \int_0^3 [x^2 yz] \,dy \, dx \, dz \\&= \int_1^5 \int_{-2}^1 \left[ \left. x^2 \dfrac{y^3}{3} z\right|_0^3 \right] dx \, dz \\&= \int_1^5 \int_{-2}^1 \dfrac{y}{2} x^2 z \,dx \, dz \\&= \int_1^5 \left[ \left. \dfrac{9}{2} \dfrac{x^3}{3} z \right|_{-2}^1 \right] dz \\&= \int_1^5 \dfrac{27}{2} z \, dz \\&= \left. \dfrac{27}{2} \dfrac{z^2}{2} \right|_1^5 = 162.\end{align*}$$

Sasa jaribu kuunganisha kwa utaratibu tofauti tu kuona kwamba tunapata jibu sawa. Chagua kuunganisha kwa heshima ya$x$ kwanza, basi$z$, basi$y$

$$\begin{align*}\iiint\limits_{B} x^2yz \,dV &= \int_0^3 \int_1^5 \int_{-2}^1 [x^2yz] \,dx\, dz\, dy \\&= \int_0^3 \int_1^5 \left[ \left. \dfrac{x^3}{3} yz \right|_{-2}^1 \right] dz \,dy \\&= \int_0^3 \int_1^5 3yz \; dz \,dy \\&= \int_0^3 \left.\left[ 3y\dfrac{z^2}{2} \right|_1^5 \right] \,dy \\&= \int_0^3 36y \; dy \\&= \left. 36\dfrac{y^2}{2} \right|_0^3 =18(9-0) =162.\end{align*}$$

Zoezi$\PageIndex{1}$

Tathmini muhimu mara tatu

$$\iiint_B z \, \sin \, x \, \cos \, y \, dV\nonumber$$

wapi$B = \big\{(x,y,z)\,|\,0 \leq x \leq \pi, \, \dfrac{3\pi}{2} \leq y \leq 2\pi, \, 1 \leq z \leq 3 \big\}$.

Kidokezo

Fuata hatua katika mfano uliopita.

Jibu

$$\iiint_B z \, \sin \, x \, \cos \, y \, dV = 8 \nonumber$$

Ushirikiano wa Triple juu ya Mkoa Mkuu Umepakana

Sisi sasa kupanua ufafanuzi wa muhimu mara tatu kukokotoa muhimu mara tatu juu ya zaidi ya jumla imepakana mkoa$E$ katika$\mathbb{R}^3$. Mikoa ya jumla iliyofungwa tutazingatia ni ya aina tatu. Kwanza, hebu$D$ kuwa kanda iliyopakana ambayo ni makadirio ya$E$ kwenye$xy$ -ndege. Tuseme kanda$E$ katika$\mathbb{R}^3$ ina fomu

$$E = \big\{(x,y,z)\,|\,(x,y) \in D, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber$$

Kwa kazi mbili$z = u_1(x,y)$ na$u_2(x,y)$, kama kwamba$u_1(x,y) \leq u_2(x,y)$ kwa wote$(x,y)$ katika$D$ kama inavyoonekana katika takwimu zifuatazo.

Kielelezo$\PageIndex{3}$: Tunaweza kuelezea kanda$E$ kama nafasi kati$u_1(x,y)$ na$u_2(x,y)$ juu ya makadirio$D$ ya$E$ kwenye$xy$ -ndege.

Triple Integral juu ya Mkoa Mkuu

Sehemu tatu ya kazi inayoendelea$f(x,y,z)$ juu ya mkoa wa jumla wa tatu-dimensional

$$E = \big\{(x,y,z)\,|\,(x,y) \in D, \, u_1(x,y) \leq z \leq u_2(x,y) \big\} \nonumber$$

katika$\mathbb{R}^3$, ambapo$D$ ni makadirio ya$E$ kwenye$xy$ ndege, ni

$$\iiint_E f(x,y,z) \,dV = \iint_D \left[\int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz \right] \, dA. \nonumber$$

Vile vile, tunaweza kufikiria jumla$D$ imepakana mkoa katika$xy$ -ndege na kazi mbili$y = u_1(x,z)$ na$y = u_2(x,z)$ vile kwamba$u_1(x,z) \leq u_2(x,z)$ kwa wote$(x,z)$ katika$D$. Basi tunaweza kuelezea kanda imara$E$ katika$\mathbb{R}^3$ kama

$$E = \big\{(x,y,z)\,|\,(x,z) \in D, \, u_1(x,z) \leq z \leq u_2(x,z) \big\} \nonumber$$ ambapo$D$ ni makadirio ya$E$ kwenye$xy$ ndege na muhimu mara tatu ni

$$\iiint_E f(x,y,z)\,dV = \iint_D \left[\int_{u_1(x,z)}^{u_2(x,z)} f(x,y,z) \,dy \right] \, dA. \nonumber$$

Hatimaye, ikiwa$D$ ni mkoa wa jumla umepakana katika$xy$ -ndege na tuna kazi mbili$x = u_1(y,z)$ na$x = u_2(y,z)$ vile kwamba$u_1(y,z) \leq u_2(y,z)$ kwa wote$(y,z)$ katika$D$, basi kanda imara$E$ katika$\mathbb{R}^3$ inaweza kuelezewa kama

$$E = \big\{(x,y,z)\,|\,(y,z) \in D, \, u_1(y,z) \leq z \leq u_2(y,z) \big\} \nonumber$$ ambapo$D$ ni makadirio ya$E$ kwenye$xy$ ndege na muhimu mara tatu ni

$$\iiint_E f(x,y,z)\,dV = \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} f(x,y,z) \, dx \right] \, dA. \nonumber$$

Kumbuka kuwa eneo$D$ katika ndege yoyote inaweza kuwa ya Aina I au Aina II kama ilivyoelezwa hapo awali. Ikiwa$D$ katika$xy$ ndege ya aina ya I (Kielelezo$\PageIndex{4}$), basi

$$E = \big\{(x,y,z)\,|\,a \leq x \leq b, \, g_1(x) \leq y \leq g_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber$$

Kielelezo$\PageIndex{4}$: sanduku$E$ ambapo makadirio$D$ katika$xy$ -ndege ni ya Aina I.

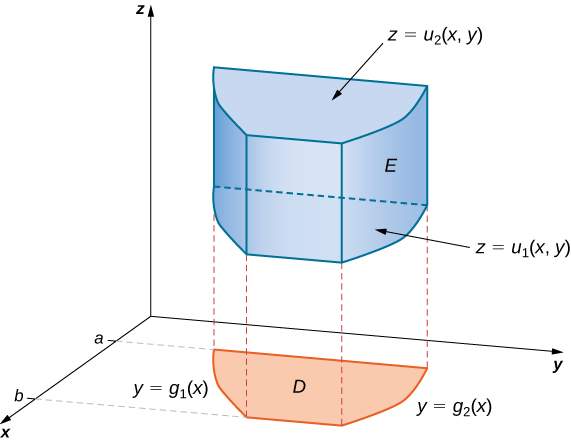
Kisha muhimu mara tatu inakuwa

$$\iiint_E f(x,y,z) \,dV = \int_a^b \int_{g_1(x)}^{g_2(x)} \int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz \, dy \, dx. \nonumber$$

Ikiwa$D$ katika$xy$ ndege ya aina ya II (Kielelezo$\PageIndex{5}$), basi

$$E = \big\{(x,y,z)\,|\,c \leq x \leq d, h_1(x) \leq y \leq h_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber$$

Kielelezo$\PageIndex{5}$: sanduku$E$ ambapo makadirio$D$ katika$xy$ -ndege ni ya Aina II.

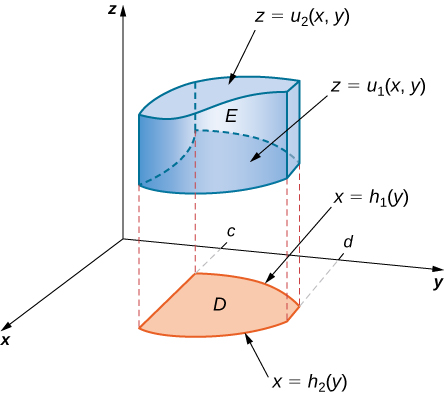
Kisha muhimu mara tatu inakuwa

$$\iiint_E f(x,y,z) \,dV = \int_{y=c}^{y=d} \int_{x=h_1(y)}^{x=h_2(y)} \int_{z=u_1(x,y)}^{z=u_2(x,y)} f(x,y,z)\,dz \, dx \, dy. \nonumber$$

Mfano$\PageIndex{3A}$: Evaluating a Triple Integral over a General Bounded Region

Tathmini muhimu mara tatu ya kazi$f(x,y,z) = 5x - 3y$ juu ya tetrahedron imara imepakana na ndege$x = 0, \, y = 0, \, z = 0$, na$x + y + z = 1$.

Suluhisho

Kielelezo$\PageIndex{6}$ kinaonyesha tetrahedron imara$E$ na makadirio yake$D$ juu ya$xy$ -ndege.

Kielelezo$\PageIndex{6}$: Imara$E$ ina makadirio$D$ juu ya$xy$ -ndege ya Aina I.

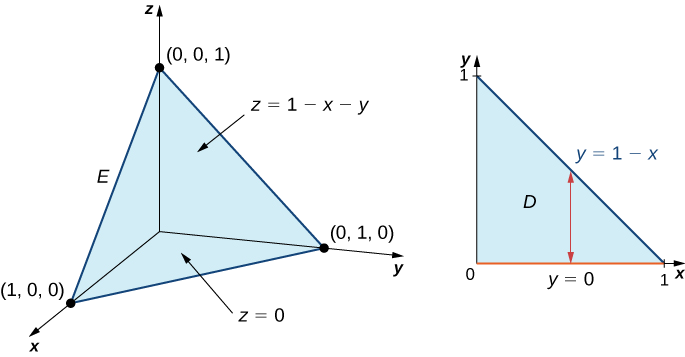
Tunaweza kuelezea tetrahedron imara kanda kama

$$E = \big\{(x,y,z)\,|\,0 \leq x \leq 1, \, 0 \leq y \leq 1 - x, \, 0 \leq z \leq 1 - x - y \big\}. \nonumber$$

Hivyo, muhimu mara tatu ni

$$\iiint_E f(x,y,z) \,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} (5x - 3y) \,dz \, dy \, dx. \nonumber$$

Ili kurahisisha hesabu, kwanza tathmini muhimu$\displaystyle \int_{z=0}^{z=1-x-y} (5x - 3y) \,dz$. Tuna

$$\int_{z=0}^{z=1-x-y} (5x - 3y) \,dz = (5x - 3y)z \bigg|_{z=0}^{z=1-x-y} = (5x - 3y)(1 - x - y).\nonumber$$

Sasa tathmini muhimu

$$\int_{y=0}^{y=1-x} (5x - 3y)(1 - x - y) \,dy, \nonumber$$

kupata

$$\int_{y=0}^{y=1-x} (5x - 3y)(1 - x - y)\,dy = \dfrac{1}{2}(x - 1)^2 (6x - 1).\nonumber$$

Hatimaye kutathmini

$$\int_{x=0}^{x=1} \dfrac{1}{2}(x - 1)^2 (6x - 1)\,dx = \dfrac{1}{12}.\nonumber$$

Kuweka yote pamoja, tuna

$$\iiint_E f(x,y,z)\,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y}(5x - 3y)\,dz \, dy \, dx = \dfrac{1}{12}.\nonumber$$

Kama vile tulivyotumia muhimu mara mbili $$\iint_D 1 \,dA \nonumber$$ ili kupata eneo la eneo la jumla$D$ lililopakana tunaweza kutumia $$\iiint_E 1\,dV \nonumber$$ ili kupata kiasi cha eneo la jumla lenye imara$E$. Mfano unaofuata unaonyesha njia.

Mfano$\PageIndex{3B}$: Finding a Volume by Evaluating a Triple Integral

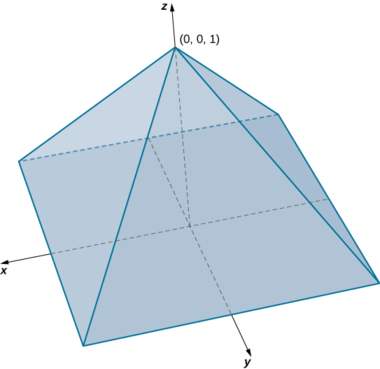
Kupata kiasi cha piramidi haki ambayo ina msingi mraba katika$xy$ -plane$[-1,1] \times [-1,1]$ na kipeo katika hatua$(0, 0, 1)$ kama inavyoonekana katika takwimu zifuatazo.

Kielelezo$\PageIndex{7}$: Kupata kiasi cha piramidi na msingi wa mraba.

Suluhisho

Katika piramidi hii thamani ya$z$ mabadiliko kutoka 0 hadi 1 na kwa kila urefu sehemu$z$ ya msalaba wa piramidi kwa thamani yoyote ya$z$ ni mraba

$$[-1 + z, \, 1 - z] \times [-1 + z, \, 1 - z].\nonumber$$

Hivyo, kiasi cha piramidi ni $$\iiint_E 1\,dV\nonumber$$ wapi

$$E = \big\{(x,y,z)\,|\,0 \leq z \leq 1, \, -1 + z \leq y \leq 1 - z, \, -1 + z \leq x \leq 1 - z \big\}.\nonumber$$

Hivyo, tuna

\ [kuanza {align*}\ IIINT_E 1\, dV &=\ int_ {z=0} ^ {z=1}\ int_ {y=-1+z} ^ {y=1-z}\ int_ {x=-1+z} ^ {x=1-z} 1\, dx\, dz\\ [5pt]
&=\ int_ {x=1-z} 1\, dx\, dz\\ [5pt] &=\ int_ z=0} ^ {z=1}\ int_ {y=-1+z} ^ {y=1-z} (2 - 2z)\, dy\\ [5pt]
&=\ int_ {z=0} ^ {z=1} (2 - 2z) ^2\, dz =\ dfrac {4} {3}. \ mwisho {align*}\]

Hivyo, kiasi cha piramidi ni vitengo vya$\dfrac{4}{3}$ ujazo.

Zoezi$\PageIndex{3}$

Fikiria nyanja imara$E = \big\{(x,y,z)\,|\,x^2 + y^2 + z^2 = 9 \big\}$. Andika muhimu mara tatu $$\iiint_E f(x,y,z) \,dV\nonumber$$ kwa ajili ya kazi ya kiholela$f$ kama muhimu iterated. Kisha tathmini hii muhimu mara tatu na$f(x,y,z) = 1$. Kumbuka kwamba hii inatoa kiasi cha nyanja kwa kutumia muhimu mara tatu.

Kidokezo

Fuata hatua katika mfano uliopita. Tumia ulinganifu.

Jibu

$$\begin{align*} \iiint_E 1\,dV = 8 \int_{x=-3}^{x=3} \int_{y=-\sqrt{9-z^2}}^{y=\sqrt{9-z^2}}\int_{z=-\sqrt{9-x^2-y^2}}^{z=\sqrt{9-x^2-y^2}} 1\,dz \, dy \, dx \\ = 36 \pi \,\text{cubic units}. \end{align*}$$

Kubadilisha Utaratibu wa Ushirikiano

Kama tumeona tayari katika integrals mara mbili juu ya mikoa ya jumla imepakana, kubadilisha utaratibu wa ushirikiano ni kufanyika mara nyingi kabisa ili kurahisisha hesabu. Kwa sehemu tatu juu ya sanduku la mstatili, utaratibu wa ushirikiano haubadili kiwango cha ugumu wa hesabu. Hata hivyo, pamoja na muhimu mara tatu juu ya eneo la jumla lililopakana, kuchagua utaratibu sahihi wa ushirikiano unaweza kurahisisha hesabu kidogo kabisa. Wakati mwingine kufanya mabadiliko kwa kuratibu polar pia inaweza kusaidia sana. Tunaonyesha mifano miwili hapa.

Mfano$\PageIndex{4}$: Changing the Order of Integration

Fikiria muhimu iterated

$$\int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=y} f(x,y,z)\,dz \, dy \, dx. \nonumber$$

Utaratibu wa ushirikiano hapa ni wa kwanza kwa heshima ya z, kisha y, na kisha x. Eleza jambo hili muhimu kwa kubadilisha utaratibu wa ushirikiano kuwa wa kwanza kwa heshima$x$, basi$z$, na kisha$y$. Thibitisha kwamba thamani ya muhimu ni sawa kama sisi basi$f (x,y,z) =xyz$.

Suluhisho

Njia bora ya kufanya hivyo ni kuchora kanda$E$ na makadirio yake kwenye kila ndege tatu za kuratibu. Hivyo, basi

$$E = \big\{(x,y,z)\,|\,0 \leq x \leq 1, \, 0 \leq y \leq x^2, \, 0 \leq z \leq y \big\}.\nonumber$$

na

$$\int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=x^2} f(x,y,z) \,dz \, dy \, dx = \iiint_E f(x,y,z)\,dV.\nonumber$$

Tunahitaji kueleza hii muhimu mara tatu kama

$$\int_{y=c}^{y=d} \int_{z=v_1(y)}^{z=v_2(y)} \int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)\,dx \, dz \, dy.\nonumber$$

Kujua kanda$E$ tunaweza kuteka makadirio yafuatayo (Kielelezo$\PageIndex{8}$):

juu ya$xy$ -ndege ni$D_1 = \big\{(x,y)\,|\, 0 \leq x \leq 1, \, 0 \leq y \leq x^2 \big\} = \{ (x,y) \,|\, 0 \leq y \leq 1, \, \sqrt{y} \leq x \leq 1 \big\},$

juu ya$yz$ -ndege ni$D_2 = \big\{(y,z) \,|\, 0 \leq y \leq 1, \, 0 \leq z \leq y^2 \big\}$, na

juu ya$xz$ -ndege ni$D_3 = \big\{(x,z) \,|\, 0 \leq x \leq 1, \, 0 \leq z \leq x^2 \big\}$.

Kielelezo$\PageIndex{8}$. Sehemu tatu za msalaba wa$E$ ndege tatu za kuratibu.

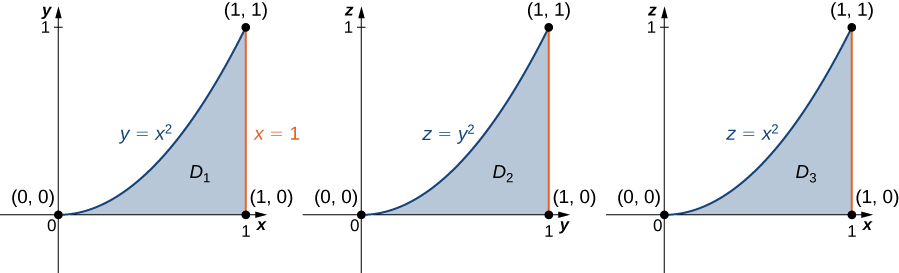
Sasa tunaweza kuelezea kanda moja$E$ kama$\big\{(x,y,z) \,|\, 0 \leq y \leq 1, \, 0 \leq z \leq y^2, \, \sqrt{y} \leq x \leq 1 \big\}$, na hivyo, muhimu mara tatu inakuwa

$$\int_{y=c}^{y=d} \int_{z=v_1(y)}^{z=v_2(y)} \int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)\,dx \, dz \, dy = \int_{y=0}^{y=1} \int_{z=0}^{z=x^2} \int_{x=\sqrt{y}}^{x=1} f(x,y,z)\,dx \, dz \, dy \nonumber$$

Sasa kudhani kwamba$f (x,y,z) = xyz$ katika kila moja ya integrals. Kisha tuna

\ [kuanza {align*}\ int_ {x=0} ^ {x=1}\ int_ {y=0} ^ {y=x^2}\ int_ {z=0} ^ {z=y ^2} xyz\, dz\, dx\, dx &=\ int_ {x=0} ^ {x=1}\ int_ {y=0}\ int_ {y=0} ^ {x = 1}\ int_ {y=0} =x^2}\ kushoto. \ kushoto [xy\ dfrac {z ^ 2} {2}\ haki|_ {z=0} ^ {z=y ^ 2}\ haki]\, dy\\, dx\\ [5pt]
&=\ int_ {x=0} ^ {x = 1}\ int_ {y=0} ^ {y=x ^ 2}\ kushoto (x\ dfrac {y ^ 5}} {2}\ kulia) dy\, dx\\ [5pt]
&=\ int_ {x=0} ^ {x=1}\ kushoto. \ kushoto [x\ dfrac {y ^ 6} {12}\ haki|_ {y=0} ^ {y=x^2}\ haki] dx\\ [5pt]
&=\ int_ {x=0} ^ {x=1}\ dfrac {x^ {13}} {12} dx =\ kushoto. \ dfrac {x^ {14}} {168}\ haki|_ {x=0} ^ {x=1}\\ [5pt]
&=\ dfrac {1} {168},\ mwisho {align*}\]

\ [kuanza {align*}\ int_ {y=0} ^ {y=1}\ int_ {z = 0} ^ {z=y ^2}\ int_ {x=\ sqrt {y}} ^ {x=1} xyz\, dx\, dz\, dy &=\ int_ {y=0} ^ {y=1}\ int_ {z=0} ^ {z=y ^ 2}\ kushoto. \ kushoto [yz\ dfrac {x^2} {2}\ haki|_ {\ sqrt {y}} ^ {1}\ haki] dz\, dy\\ [5pt]
&=\ int_ {y=0} ^ {y=1}\ int_ {z=0} ^ {z=y ^ 2}\ kushoto (\ dfrac} {yz} 2} - {2}\ dfrac {y ^ 2z} {2}\ haki) dz\, dy\\ [5pt]
&=\ int_ {y=0} ^ {y=1}\ kushoto. \ kushoto [\ dfrac {yz ^ 2} {4} -\ dfrac {y ^ 2z ^ 2} {4}\ haki|_ {z=0} ^ {z=y ^ 2}\ haki] dy\\ [5pt]
&=\ int_ {y=0} ^ {y=1}\ kushoto (\ dfrac {y ^ 5} {4} -\ dfrac c {y ^ 6} {4}\ kulia) dy\\ [5pt]
&=\ kushoto. \ kushoto (\ dfrac {y ^ 6} {24} -\ dfrac {y ^ 7} {28}\ haki)\ haki|_ {y=0} ^ {y=1}\\ [5pt]
&=\ dfrac {1} {168}. \ mwisho {align*}\ nonumber\]

majibu mechi.

Zoezi$\PageIndex{4}$

Andika tano integrals tofauti iterated sawa na muhimu kutokana

$$\int_{z=0}^{z=4} \int_{y=0}^{y=4-z} \int_{x=0}^{x=\sqrt{y}} f(x,y,z) \, dx \, dy \, dz.\nonumber$$

Kidokezo

Fuata hatua katika mfano uliopita, kwa kutumia kanda$E$ kama$\big\{(x,y,z) \,|\, 0 \leq z \leq 4, \, 0 \leq y \leq 4 - z, \, 0 \leq x \leq \sqrt{y} \big\}$, na kuelezea na mchoro makadirio kwenye kila ndege tatu, mara tano tofauti.

Jibu

$$(i) \, \int_{z=0}^{z=4} \int_{x=0}^{x=\sqrt{4-z}} \int_{y=x^2}^{y=4-z} f(x,y,z) \, dy \, dx \, dz, \, (ii) \, \int_{y=0}^{y=4} \int_{z=0}^{z=4-y} \int_{x=0}^{x=\sqrt{y}} f(x,y,z) \,dx \, dz \, dy, \,(iii) \, \int_{y=0}^{y=4} \int_{x=0}^{x=\sqrt{y}} \int_{z=0}^{Z=4-y} f(x,y,z) \,dz \, dx \, dy, \, \nonumber$$

$$(iv) \, \int_{x=0}^{x=2} \int_{y=x^2}^{y=4} \int_{z=0}^{z=4-y} f(x,y,z) \,dz \, dy \, dx, \, (v) \int_{x=0}^{x=2} \int_{z=0}^{z=4-x^2} \int_{y=x^2}^{y=4-z} f(x,y,z) \,dy \, dz \, dx \nonumber$$

Mfano$\PageIndex{5}$: Changing Integration Order and Coordinate Systems

Tathmini muhimu mara tatu

$$\iiint_{E} \sqrt{x^2 + z^2} \,dV, \nonumber$$

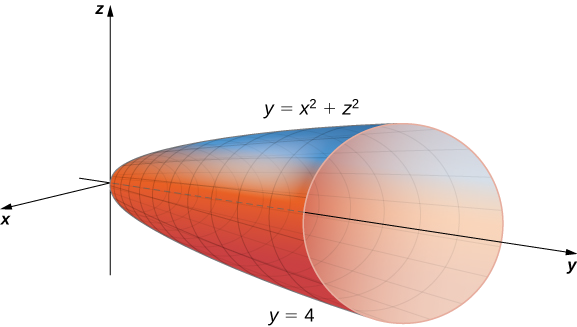
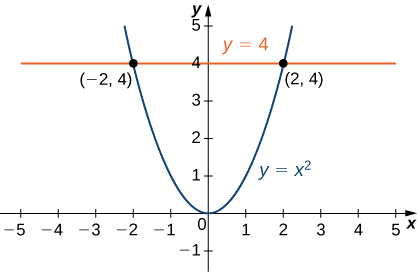
$E$wapi eneo lililopakana na paraboloid$y = x^2 + z^2$ (Kielelezo$\PageIndex{9}$) na ndege$y = 4$.

Kielelezo$\PageIndex{9}$. Kuunganisha muhimu mara tatu juu ya paraboloid.

Suluhisho

Makadirio ya kanda imara$E$ kwenye$xy$ -ndege ni eneo lililopakana hapo juu$y = 4$ na chini na parabola$y = x^2$ kama inavyoonekana.

Kielelezo$\PageIndex{10}$. Sehemu ya msalaba katika$xy$ -ndege ya paraboloid katika Kielelezo$\PageIndex{9}$.

Hivyo, tuna

$$E = \big\{(x,y,z) \,|\, -2 \leq x \leq 2, \, x^2 \leq y \leq 4, \, -\sqrt{y - x^2} \leq z \sqrt{y - x^2} \big\}.\nonumber$$

Muhimu wa tatu unakuwa

$$\iiint_E \sqrt{x^2 + z^2} \,dV = \int_{x=-2}^{x=2} \int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}} \sqrt{x^2 + z^2} \,dz \, dy \, dx.\nonumber$$

Maneno haya ni vigumu kukokotoa, hivyo fikiria makadirio ya$E$ kwenye$xz$ -plane. Hii ni disc ya mviringo$x^2 + z^2 \leq 4$. Hivyo sisi kupata

$$\iiint_E \sqrt{x^2 + z^2} \,dV = \int_{x=-2}^{x=2} \int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}} \sqrt{x^2 + z^2} \,dz \, dy \, dx = \int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2+z^2}^{y=4} \sqrt{x^2 + z^2} \,dy \, dz \, dx.\nonumber$$

Hapa utaratibu wa ushirikiano hubadilika kutoka kuwa wa kwanza$x$ kwa heshima$y$ na$z$ kisha kuwa wa kwanza kwa$y$ heshima$z$ na kisha kwenda$x$. Hivi karibuni itakuwa wazi jinsi mabadiliko haya yanaweza kuwa na manufaa kwa hesabu. Tuna

$$\int_{x=-2}^{x=2} \int_{z=\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2+z^2}^{y=4} \sqrt{x^2 + z^2} \,dy \, dz \, dx = \int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} (4 - x^2 - z^2) \sqrt{x^2 + z^2} \,dz \, dx.\nonumber$$

Sasa tumia badala ya polar$x = r \, \cos \, \theta, \, z = r \, \sin \, \theta$, na$dz \, dx = r \, dr \, d\theta$ katika$xz$ -ndege. Hii kimsingi ni kitu kimoja kama wakati sisi kutumika kuratibu Polar katika$xy$ -plane, isipokuwa sisi ni kuchukua nafasi$y$ kwa$z$. Kwa hiyo mipaka ya mabadiliko ya ushirikiano na tuna, kwa kutumia$r^2 = x^2 + z^2$,

$$\int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} (4 - x^2 - z^2) \sqrt{x^2 + z^2}\,dz \, dx = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=2} (4 - r^2) rr \, dr \, d\theta = \int_0^{2\pi} \left. \left[ \dfrac{4r^3}{3} - \dfrac{r^5}{5} \right|_0^2 \right] \, d\theta = \int_0^{2\pi} \dfrac{64}{15} \,d\theta = \dfrac{128\pi}{15}\nonumber$$

Wastani wa Thamani ya Kazi ya Vigezo Tatu

Kumbuka kwamba tuligundua thamani ya wastani ya kazi ya vigezo viwili kwa kutathmini muhimu mara mbili juu ya mkoa kwenye ndege na kisha kugawa kwa eneo la kanda. Vile vile, tunaweza kupata thamani ya wastani wa kazi katika vigezo tatu kwa kutathmini muhimu mara tatu juu ya mkoa imara na kisha kugawa kwa kiasi cha imara.

Wastani wa Thamani ya Kazi ya Vigezo Tatu

Ikiwa$f(x,y,z)$ ni integrable juu ya mkoa imara$E$ imepakana na kiasi chanya,$V \, (E),$ basi thamani ya wastani ya kazi ni

$$f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \, dV. \nonumber$$

Kumbuka kuwa kiasi ni

$$V \, (E) = \iiint_E 1 \,dV. \nonumber$$

Mfano$\PageIndex{6}$: Finding an Average Temperature

Joto katika hatua$(x,y,z)$ ya imara$E$ imefungwa na ndege kuratibu na ndege$x + y + z = 1$ ni$T(x,y,z) = (xy + 8z + 20) \, \text{°}\text{C}$. Pata joto la wastani juu ya imara.

Suluhisho

Tumia theorem iliyotolewa hapo juu na muhimu tatu ili kupata namba na denominator. Kisha fanya mgawanyiko. Kumbuka kwamba ndege$x + y + z = 1$ ina intercepts$(1,0,0), \, (0,1,0),$ na$(0,0,1)$. Kanda$E$ inaonekana kama

$$E = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq 1 - x, \, 0 \leq z \leq 1 - x - y \big\}.\nonumber$$

Hivyo muhimu mara tatu ya joto ni

$$\iiint_E f(x,y,z) \,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} (xy + 8z + 20) \, dz \, dy \, dx = \dfrac{147}{40}. \nonumber$$

Tathmini ya kiasi ni

$$V \, (E) = \iiint_E 1\,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} 1 \,dz \, dy \, dx = \dfrac{1}{6}. \nonumber$$

Hivyo thamani ya wastani ni

$$T_{ave} = \dfrac{147/40}{1/6} = \dfrac{6(147)}{40} = \dfrac{441}{20} \, \text{°}\text{C} \nonumber$$ .

Zoezi$\PageIndex{6}$

Pata thamani ya wastani ya kazi$f(x,y,z) = xyz$ juu ya mchemraba na pande za urefu wa vitengo 4 katika octant ya kwanza na vertex moja katika asili na kando sambamba na shoka za kuratibu.

Kidokezo

Fuata hatua katika mfano uliopita.

Jibu

$f_{ave} = 8$

Dhana muhimu

• Kukokotoa muhimu mara tatu tunatumia theorem Fubini ya, ambayo inasema kwamba kama$f(x,y,z)$ ni kuendelea juu ya sanduku mstatili$B = [a,b] \times [c,d] \times [e,f]$, basi $$\iiint_B f(x,y,z) \,dV = \int_e^f \int_c^d \int_a^b f(x,y,z) \, dx \, dy \, dz \nonumber$$ na pia ni sawa na yoyote ya nyingine tano orderings inawezekana kwa iterated tatu muhimu.
• Ili kukokotoa kiasi cha kanda ya jumla imara imepakana$E$ tunatumia muhimu mara tatu $$V \, (E) = \iiint_E 1 \,dV. \nonumber$$
• Kubadilishana utaratibu wa integrals iterated haina mabadiliko ya jibu. Kwa kweli, kubadilishana utaratibu wa ushirikiano kunaweza kusaidia kurahisisha hesabu.
• Ili kukokotoa thamani ya wastani ya kazi juu ya mkoa wa jumla wa tatu-dimensional, tunatumia $$f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \,dV. \nonumber$$

Mlinganyo muhimu

• Triple muhimu

$$\lim_{l,m,n \rightarrow \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*) \,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber$$

faharasa

mara tatu muhimu

muhimu mara tatu ya kazi ya kuendelea$f(x,y,z)$ juu ya mstatili sanduku imara$B$ ni kikomo cha Riemann jumla kwa kazi ya vigezo tatu, kama kikomo hii ipo