15.3: Integrals mara mbili katika Kuratibu Polar

Malengo ya kujifunza

• Tambua muundo wa muhimu mara mbili juu ya mkoa wa mstatili wa polar.
• Kutathmini muhimu mara mbili katika kuratibu polar kwa kutumia muhimu iterated.
• Tambua muundo wa muhimu mara mbili juu ya kanda ya polar ya jumla.
• Tumia integrals mara mbili katika kuratibu polar kuhesabu maeneo na kiasi.

Mara mbili integrals wakati mwingine ni rahisi sana kutathmini kama sisi kubadilisha kuratibu mstatili kwa kuratibu polar. Hata hivyo, kabla ya kuelezea jinsi ya kufanya mabadiliko haya, tunahitaji kuanzisha dhana ya mara mbili muhimu katika mkoa wa polar mstatili.

Mikoa ya mviringo ya Ushirikiano

Wakati sisi defined muhimu mara mbili kwa ajili ya kazi ya kuendelea katika kuratibu mstatili - kusema,$g$ juu ya kanda$R$ katika$xy$ -ndege-sisi$R$ kugawanywa katika subrectangles na pande sambamba na shoka kuratibu. Pande hizi zina ama mara kwa mara$x$ -maadili na/au mara kwa mara$y$ -maadili. Katika kuratibu polar, sura tunayofanya kazi nayo ni mstatili wa polar, ambao pande zake zina maadili ya mara kwa mara na/au$r$ maadili ya mara kwa mara$\theta$. Hii ina maana tunaweza kuelezea Mstatili Polar kama katika Kielelezo$\PageIndex{1a}$, kwa$R = \{(r,\theta)\,|\, a \leq r \leq b, \, \alpha \leq \theta \leq \beta\}$.

Kielelezo$\PageIndex{1}$: (a) Mstatili wa polar$R$ (b) umegawanywa katika subrectangles$R_{ij}$ (c) Karibu na subrectangles.

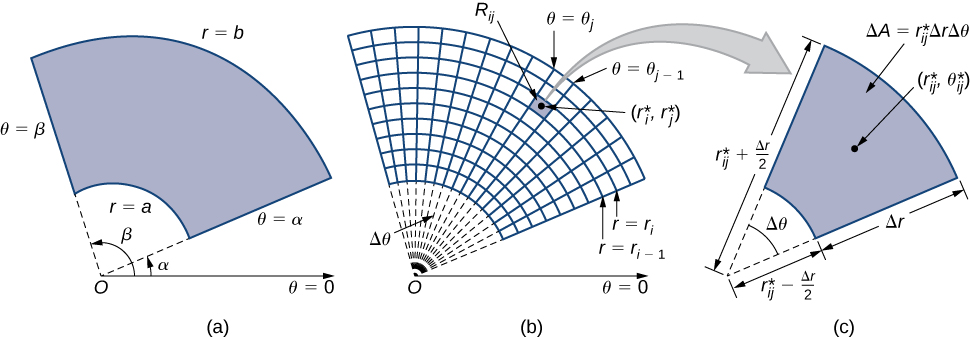
Katika sehemu hii, tunatafuta kuunganisha juu ya rectangles polar. Fikiria kazi$f(r,\theta)$ juu ya mstatili wa polar$R$. Tunagawanya muda$[a,b]$ katika$m$ sehemu ndogo$[r_{i-1}, r_i]$ za urefu$\Delta r = (b - a)/m$ na kugawanya muda$[\alpha, \beta]$ katika$n$ sehemu ndogo$[\theta_{i-1}, \theta_i]$ za upana$\Delta \theta = (\beta - \alpha)/n$. Hii ina maana kwamba miduara$r = r_i$ na mionzi$\theta = \theta_i$$1 \leq i \leq m$ na$1 \leq j \leq n$ kugawanya mstatili wa polar$R$ katika subrectangles ndogo ndogo$R_{ij}$ (Kielelezo$\PageIndex{1b}$).

Kama hapo awali, tunahitaji kupata eneo$\Delta A$ la subrectangle ya polar$R_{ij}$ na kiasi cha “polar” cha sanduku nyembamba hapo juu$R_{ij}$. Kumbuka kwamba, katika mduara wa radius urefu$r$$s$ wa arc subtended na angle ya kati ya$\theta$ radians ni$s = r\theta$. Angalia kwamba mstatili wa polar$R_{ij}$ inaonekana sana kama trapezoid na pande$r_{i-1}\Delta \theta$ zinazofanana$r_i\Delta \theta$ na na kwa upana$\Delta r$. Hivyo eneo la subrectangle polar$R_{ij}$ ni

$$\Delta A = \frac{1}{2} \Delta r (r_{i-1} \Delta \theta + r_i \Delta \theta ). \nonumber$$

Kurahisisha na kuruhusu

$$r_{ij}^* = \frac{1}{2}(r_{i-1}+r_i) \nonumber$$

tuna$\Delta A = r_{ij}^* \Delta r \Delta \theta$.

Kwa hiyo, kiasi cha polar cha sanduku nyembamba hapo juu$R_{ij}$ (Kielelezo$\PageIndex{2}$) ni

$$f(r_{ij}^*, \theta_{ij}^*) \Delta A = f(r_{ij}^*, \theta_{ij}^*)r_{ij}^* \Delta r \Delta \theta. \nonumber$$

Kielelezo$\PageIndex{2}$: Kutafuta kiasi cha sanduku nyembamba juu ya mstatili wa polar$R_{ij}$.

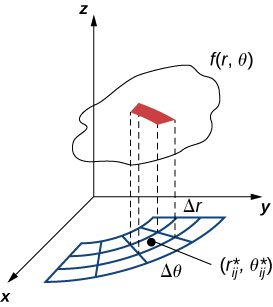
Kutumia wazo sawa kwa subrectangles zote na kuhesabu kiasi cha masanduku ya mstatili, tunapata jumla ya Riemann mara mbili kama

$$\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) r_{ij}^* \Delta r \Delta \theta. \nonumber$$

Kama tulivyoona kabla, sisi kupata makadirio bora kwa kiasi Polar ya imara juu ya kanda$R$ wakati sisi basi$m$ na$n$ kuwa kubwa. Kwa hiyo, tunafafanua kiasi cha polar kama kikomo cha jumla ya Riemann mara mbili,

$$V = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) r_{ij}^* \Delta r \Delta \theta. \nonumber$$

Hii inakuwa maneno kwa ajili ya muhimu mara mbili.

Ufafanuzi: muhimu mara mbili katika kuratibu polar

Muhimu wa mara mbili wa kazi$f(r, \theta)$ juu ya mkoa wa mstatili wa polar$R$ katika$r\theta$ -ndege hufafanuliwa kama

$$\begin{align} \iint_R f(r, \theta)dA &= \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) \Delta A \\[4pt] &= \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*,\theta_{ij}^*)r_{ij}^* \Delta r \Delta \theta. \end{align} \nonumber$$

Tena, kama katika sehemu ya Double Integrals juu ya Mikoa Rectangular, muhimu mara mbili juu ya mkoa polar mstatili inaweza kuwa walionyesha kama muhimu iterated katika kuratibu Polar. Hivyo,

$$\iint_R f(r, \theta)\,dA = \iint_R f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=a}^{r=b} f(r,\theta) \,r \, dr \, d\theta. \nonumber$$

Angalia kwamba maneno ya kubadilishwa$dA$ yanabadilishwa na$r \, dr \, d\theta$ wakati wa kufanya kazi katika kuratibu za polar. Njia nyingine ya kuangalia polar mara mbili muhimu ni kubadili mara mbili muhimu katika kuratibu mstatili na badala. Wakati kazi$f$ inapewa katika suala la$x$ na$y$ kutumia$x = r \, \cos \, \theta, \, y = r \, \sin \, \theta$, na$dA = r \, dr \, d\theta$ kuibadilisha

$$\iint_R f(x,y) \,dA = \iint_R f(r \, \cos \, \theta, \, r \, \sin \, \theta ) \,r \, dr \, d\theta. \nonumber$$

Kumbuka kuwa mali yote waliotajwa katika sehemu ya Double Integrals juu ya Mikoa Rectangular kwa muhimu mara mbili katika kuratibu mstatili kushikilia kweli kwa muhimu mara mbili katika kuratibu Polar pia, ili tuweze kuzitumia bila kusita.

Mfano$\PageIndex{1A}$: Sketching a Polar Rectangular Region

Mchoro mkoa wa mstatili wa polar

$$R = \{(r, \theta)\,|\,1 \leq r \leq 3, 0 \leq \theta \leq \pi \}. \nonumber$$

Suluhisho

Kama tunavyoona kutoka Kielelezo$\PageIndex{3}$,$r = 1$ na$r = 3$ ni duru ya Radius 1 na 3 na$0 \leq \theta \leq \pi$ inashughulikia nzima juu nusu ya ndege. Hivyo kanda$R$ inaonekana kama bendi ya semicircular.

Kielelezo$\PageIndex{3}$: Eneo la polar$R$ liko kati ya semicircles mbili.

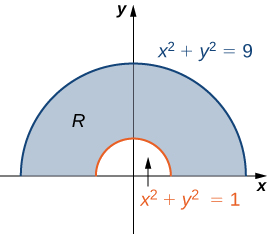
Sasa kwa kuwa tumeweka mkoa wa mstatili wa polar, hebu tuonyeshe jinsi ya kutathmini muhimu mara mbili juu ya mkoa huu kwa kutumia viwianishi vya polar.

Mfano$\PageIndex{1B}$: Evaluating a Double Integral over a Polar Rectangular Region

Kutathmini muhimu$\displaystyle \iint_R 3x \, dA$ juu ya kanda$R = \{(r, \theta)\,|\,1 \leq r \leq 2, \, 0 \leq \theta \leq \pi \}.$

Suluhisho

Kwanza tunachora takwimu sawa na Kielelezo$\PageIndex{3}$, lakini kwa radius ya nje$r=2$. Kutoka takwimu tunaweza kuona kwamba tuna

$$\begin{align*} \iint_R 3x \, dA &= \int_{\theta=0}^{\theta=\pi} \int_{r=1}^{r=2} 3r \, \cos \, \theta \,r \, dr \, d\theta \quad\text{Use an integral with correct limits of integration.} \\ &= \int_{\theta=0}^{\theta=\pi} \cos \, \theta \left[\left. r^3\right|_{r=1}^{r=2}\right] d\theta \quad\text{Integrate first with respect to $r$.} \\ &=\int_{\theta=0}^{\theta=\pi} 7 \, \cos \, \theta \, d\theta \\ &= 7 \, \sin \, \theta \bigg|_{\theta=0}^{\theta=\pi} = 0. \end{align*}$$

Zoezi$\PageIndex{1}$

Mchoro kanda$D = \{ (r,\theta) \vert 1\leq r \leq 2, \, -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2} \}$, na tathmini$\displaystyle \iint_R x \, dA$.

Kidokezo

Fuata hatua katika Mfano$\PageIndex{1A}$.

Jibu

$\frac{14}{3}$

Mfano$\PageIndex{2A}$: Evaluating a Double Integral by Converting from Rectangular Coordinates

Tathmini muhimu

$$\iint_R (1 - x^2 - y^2) \,dA \nonumber$$

$R$wapi mduara wa kitengo kwenye$xy$ -ndege.

Suluhisho

Mkoa$R$ ni mduara wa kitengo, hivyo tunaweza kuielezea kama$R = \{(r, \theta )\,|\,0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi \}$.

Kutumia uongofu$x = r \, \cos \, \theta, \, y = r \, \sin \, \theta$, na$dA = r \, dr \, d\theta$, tuna

$$\begin{align*} \iint_R (1 - x^2 - y^2) \,dA &= \int_0^{2\pi} \int_0^1 (1 - r^2) \,r \, dr \, d\theta \\[4pt] &= \int_0^{2\pi} \int_0^1 (r - r^3) \,dr \, d\theta \\ &= \int_0^{2\pi} \left[\frac{r^2}{2} - \frac{r^4}{4}\right]_0^1 \,d\theta \\&= \int_0^{2\pi} \frac{1}{4}\,d\theta = \frac{\pi}{2}. \end{align*}$$

Mfano$\PageIndex{2B}$: Evaluating a Double Integral by Converting from Rectangular Coordinates

Kutathmini muhimu $$\displaystyle \iint_R (x + y) \,dA \nonumber$$ ambapo$R = \big\{(x,y)\,|\,1 \leq x^2 + y^2 \leq 4, \, x \leq 0 \big\}.$

Suluhisho

Tunaweza kuona kwamba$R$ ni kanda annular ambayo inaweza kubadilishwa kwa kuratibu polar na ilivyoelezwa kama$R = \left\{(r, \theta)\,|\,1 \leq r \leq 2, \, \frac{\pi}{2} \leq \theta \leq \frac{3\pi}{2} \right\}$ (angalia grafu ifuatayo).

Kielelezo$\PageIndex{4}$: mkoa annular ya ushirikiano$R$.

Hivyo, kwa kutumia uongofu$x = r \, \cos \, \theta, \, y = r \, \sin \, \theta$, na$dA = r \, dr \, d\theta$, tuna

$$\begin{align*} \iint_R (x + y)\,dA &= \int_{\theta=\pi/2}^{\theta=3\pi/2} \int_{r=1}^{r=2} (r \, \cos \, \theta + r \, \sin \, \theta) r \, dr \, d\theta \\ &= \left(\int_{r=1}^{r=2} r^2 \, dr\right)\left(\int_{\pi/2}^{3\pi/2} (\cos \, \theta + \sin \, \theta)\,d\theta\right) \\ &= \left. \left[\frac{r^3}{3}\right]_1^2 [\sin \, \theta - \cos \, \theta] \right|_{\pi/2}^{3\pi/2} \\ &= - \frac{14}{3}. \end{align*}$$

Zoezi$\PageIndex{2}$

Tathmini muhimu $$\displaystyle \iint_R (4 - x^2 - y^2)\,dA \nonumber$$ ambapo$R$ ni mduara wa radius 2 kwenye$xy$ -ndege.

Kidokezo

Fuata hatua katika mfano uliopita.

Jibu

$8\pi$

Mkuu Polar Mikoa ya Ushirikiano

Kutathmini muhimu mara mbili ya kazi ya kuendelea na integrals iterated juu ya mikoa ya jumla Polar, tunaona aina mbili za mikoa, sawa na Aina ya I na Aina II kama kujadiliwa kwa kuratibu mstatili katika sehemu ya Integrals Double juu ya Mikoa Mkuu. Ni kawaida zaidi kuandika equations polar kama$r = f(\theta)$ kuliko$\theta = f(r)$, hivyo sisi kuelezea jumla polar eneo kama$R = \{(r, \theta)\,|\,\alpha \leq \theta \leq \beta, \, h_1 (\theta) \leq r \leq h_2(\theta)\}$ (Kielelezo$\PageIndex{5}$).

Kielelezo$\PageIndex{5}$: General polar mkoa kati$\alpha \leq \theta \leq \beta$ na$h_1(\theta) \leq r \leq h_2(\theta)$.

Theorem: Integrals mara mbili juu ya Mikoa Mkuu Polar

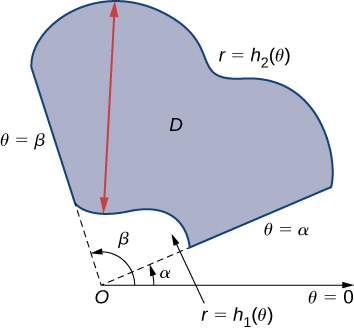
Kama$f(r, \theta)$ ni kuendelea katika eneo la jumla Polar$D$ kama ilivyoelezwa hapo juu, basi

$$\iint_D f(r, \theta ) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r=h_2(\theta)} f(r,\theta) \, r \, dr \, d\theta. \nonumber$$

Mfano$\PageIndex{3}$: Evaluating a Double Integral over a General Polar Region

Tathmini muhimu

$$\iint_D r^2 \sin \theta \, r \, dr \, d\theta \nonumber$$

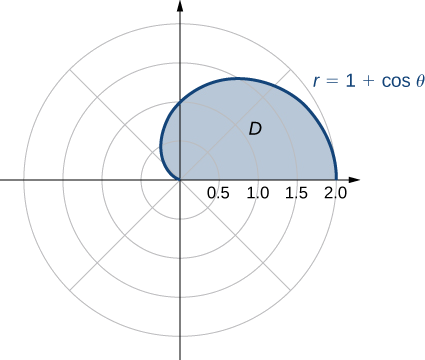
$D$wapi eneo lililofungwa na mhimili wa polar na nusu ya juu ya cardioid$r = 1 + \cos \, \theta$.

Suluhisho

Tunaweza kuelezea kanda$D$ kama$\{(r, \theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 1 + \cos \, \theta\}$ inavyoonekana katika Kielelezo$\PageIndex{6}$.

Kielelezo$\PageIndex{6}$: Kanda$D$ ni nusu ya juu ya cardioid.

Hivyo, tuna

$$\begin{align*} \iint_D r^2 \sin \, \theta \, r \, dr \, d\theta &= \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=1+\cos \theta} (r^2 \sin \, \theta) \,r \, dr \, d\theta \\ &= \frac{1}{4}\left.\int_{\theta=0}^{\theta=\pi}[r^4] \right|_{r=0}^{r=1+\cos \, \theta} \sin \, \theta \, d\theta \\ &= \frac{1}{4} \int_{\theta=0}^{\theta=\pi} (1 + \cos \, \theta )^4 \sin \, \theta \, d\theta \\ &= - \frac{1}{4} \left[ \frac{(1 + \cos \, \theta)^5}{5}\right]_0^{\pi} = \frac{8}{5}.\end{align*}$$

Zoezi$\PageIndex{3}$

Tathmini muhimu

$$\iint_D r^2 \sin^2 2\theta \,r \, dr \, d\theta \nonumber$$

wapi$D = \left\{ (r,\theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \sqrt{\cos \, 2\theta} \right\}$.

Kidokezo

Grafu kanda na ufuate hatua katika mfano uliopita.

Jibu

$\frac{\pi}{8}$

Maeneo ya Polar na Kiasi

Kama ilivyo katika kuratibu mstatili, ikiwa imara$S$ imefungwa na uso$z = f(r, \theta)$, pamoja na nyuso$r = a, \, r = b, \, \theta = \alpha$, na$\theta = \beta$, tunaweza kupata kiasi$V$ cha$S$ ushirikiano mara mbili, kama

$$V = \iint_R f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=a}^{r=b} f(r,\theta)\, r \, dr \, d\theta. \nonumber$$

Ikiwa msingi wa imara unaweza kuelezewa kama$D = \{(r, \theta)|\alpha \leq \theta \leq \beta, \, h_1 (\theta) \leq r \leq h_2(\theta)\}$, basi muhimu mara mbili kwa kiasi inakuwa

$$V = \iint_D f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r=h_2(\theta)} f(r,\theta) \,r \, dr \, d\theta. \nonumber$$

Sisi kuonyesha wazo hili na baadhi ya mifano.

Mfano$\PageIndex{4A}$: Finding a Volume Using a Double Integral

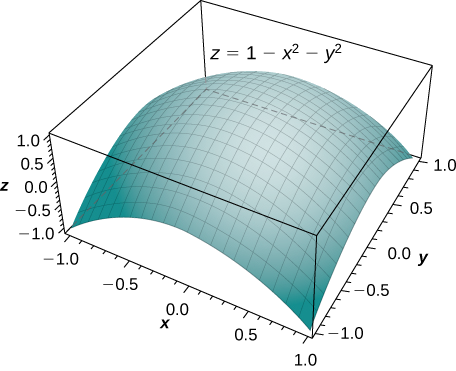
Pata kiasi cha imara iliyo chini ya paraboloid$z = 1 - x^2 - y^2$ na juu ya mduara wa kitengo kwenye$xy$ -ndege (Kielelezo$\PageIndex{7}$).

Kielelezo$\PageIndex{7}$: Kutafuta kiasi cha imara chini ya paraboloid na juu ya mduara wa kitengo.

Suluhisho

Kwa njia ya ushirikiano mara mbili, tunaweza kuona kwamba kiasi ni muhimu iterated ya fomu

$$\displaystyle \iint_R (1 - x^2 - y^2)\,dA \nonumber$$

wapi$R = \big\{(r, \theta)\,|\,0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi\big\}$.

Ushirikiano huu ulionyeshwa kabla katika Mfano$\PageIndex{2A}$, hivyo kiasi ni vitengo vya$\frac{\pi}{2}$ ujazo.

Mfano$\PageIndex{4B}$: Finding a Volume Using Double Integration

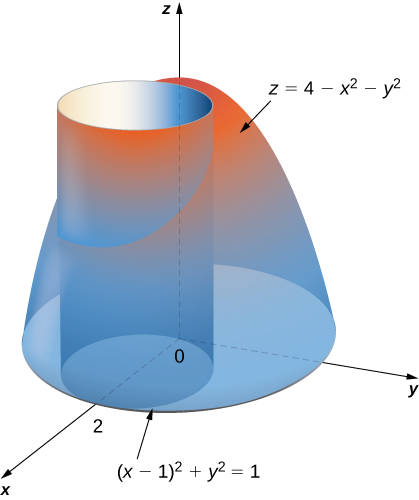
Pata kiasi cha imara iliyo chini ya paraboloid$z = 4 - x^2 - y^2$ na juu ya disk$(x - 1)^2 + y^2 = 1$ kwenye$xy$ -ndege. Angalia paraboloid katika Kielelezo$\PageIndex{8}$ intersecting silinda$(x - 1)^2 + y^2 = 1$ juu$xy$ -ndege.

Kielelezo$\PageIndex{8}$: Kutafuta kiasi cha imara na kofia ya paraboloid na msingi wa mviringo.

Suluhisho

Kwanza kubadilisha disk kwa$(x - 1)^2 + y^2 = 1$ kuratibu polar. Kupanua muda wa mraba, tuna$x^2 - 2x + 1 + y^2 = 1$. Kisha kurahisisha kupata$x^2 + y^2 = 2x$, ambayo katika kuratibu polar inakuwa$r^2 = 2r \, \cos \, \theta$ na kisha ama$r = 0$ au$r = 2 \, \cos \, \theta$. Vile vile, equation ya paraboloid inabadilika$z = 4 - r^2$. Kwa hiyo, tunaweza kuelezea disk$(x - 1)^2 + y^2 = 1$ juu ya$xy$ ndege kama kanda

$$D = \{(r,\theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \, \cos \theta\}. \nonumber$$

Hivyo kiasi cha imara imefungwa juu na paraboloid$z = 4 - x^2 - y^2$ na chini na$r = 2 \, \cos \theta$ ni

$$\begin{align*} V &= \iint_D f(r, \theta) \,r \, dr \, d\theta \\&= \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=2 \, \cos \, \theta} (4 - r^2) \,r \, dr \, d\theta\\ &= \int_{\theta=0}^{\theta=\pi}\left.\left[4\frac{r^2}{2} - \frac{r^4}{4}\right|_0^{2 \, \cos \, \theta}\right]d\theta \\ &= \int_0^{\pi} [8 \, \cos^2\theta - 4 \, \cos^4\theta]\,d\theta \\&= \left[\frac{5}{2}\theta + \frac{5}{2} \sin \, \theta \, \cos \, \theta - \sin \, \theta \cos^3\theta \right]_0^{\pi} = \frac{5}{2}\pi\; \text{units}^3. \end{align*}$$

Angalia katika mfano unaofuata kwamba ushirikiano si rahisi kila wakati na kuratibu polar. Ukamilifu wa ushirikiano unategemea kazi na pia kwenye eneo ambalo tunahitaji kufanya ushirikiano. Ikiwa kanda ina kujieleza zaidi ya asili katika kuratibu za polar au ikiwa$f$ ina antiderivative rahisi katika kuratibu polar, basi mabadiliko katika kuratibu polar ni sahihi; vinginevyo, tumia kuratibu mstatili.

Mfano$\PageIndex{5A}$: Finding a Volume Using a Double Integral

Pata kiasi cha kanda iliyo chini ya paraboloid$z = x^2 + y^2$ na juu ya pembetatu iliyofungwa na mistari$y = x, \, x = 0$, na$x + y = 2$ katika$xy$ -ndege.

Suluhisho

Kwanza kuchunguza kanda ambayo tunahitaji kuanzisha muhimu mara mbili na paraboloid kuandamana.

Kielelezo$\PageIndex{9}$: Kutafuta kiasi cha imara chini ya paraboloid na juu ya pembetatu iliyotolewa.

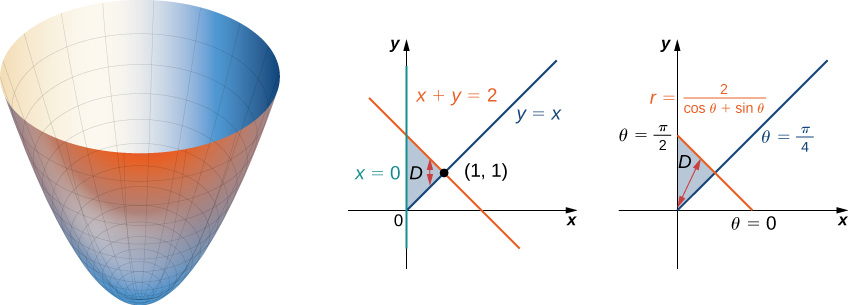
Mkoa$D$ ni$\{(x,y)\,|\,0 \leq x \leq 1, \, x \leq y \leq 2 - x\}$. Kubadili mistari$y = x, \, x = 0$, na$x + y = 2$ katika$xy$ -ndege kwa kazi ya$r$ na$\theta$ tuna$\theta = \pi/4, \, \theta = \pi/2$, na$r = 2 / (\cos \, \theta + \sin \, \theta)$, kwa mtiririko huo. Kuweka kanda kwenye$xy$ ndege, tunaona kwamba inaonekana kama$D = \{(r, \theta)\,|\,\pi/4 \leq \theta \leq \pi/2, \, 0 \leq r \leq 2/(\cos \, \theta + \sin \, \theta)\}$.

Sasa kubadilisha equation ya uso inatoa$z = x^2 + y^2 = r^2$. Kwa hiyo, kiasi cha imara kinatolewa na muhimu mara mbili

$$\begin{align*} V &= \iint_D f(r, \theta)\,r \, dr \, d\theta \\&= \int_{\theta=\pi/4}^{\theta=\pi/2} \int_{r=0}^{r=2/ (\cos \, \theta + \sin \, \theta)} r^2 r \, dr d\theta \\ &= \int_{\pi/4}^{\pi/2}\left[\frac{r^4}{4}\right]_0^{2/(\cos \, \theta + \sin \, \theta)} d\theta \\ &=\frac{1}{4}\int_{\pi/4}^{\pi/2} \left(\frac{2}{\cos \, \theta + \sin \, \theta}\right)^4 d\theta \\ &= \frac{16}{4} \int_{\pi/4}^{\pi/2} \left(\frac{1}{\cos \, \theta + \sin \, \theta} \right)^4 d\theta \\&= 4\int_{\pi/4}^{\pi/2} \left(\frac{1}{\cos \, \theta + \sin \, \theta}\right)^4 d\theta. \end{align*}$$

Kama unaweza kuona, hii muhimu ni ngumu sana. Hivyo, tunaweza badala kutathmini hii muhimu mara mbili katika kuratibu mstatili kama

$$V = \int_0^1 \int_x^{2-x} (x^2 + y^2) \,dy \, dx. \nonumber$$

Kutathmini anatoa

$$\begin{align*} V &= \int_0^1 \int_x^{2-x} (x^2 + y^2) \,dy \, dx \\&= \int_0^1 \left.\left[x^2y + \frac{y^3}{3}\right]\right|_x^{2-x} dx\\ &= \int_0^1 \frac{8}{3} - 4x + 4x^2 - \frac{8x^3}{3} \,dx \\ &= \left.\left[\frac{8x}{3} - 2x^2 + \frac{4x^3}{3} - \frac{2x^4}{3}\right]\right|_0^1 \\&= \frac{4}{3} \; \text{units}^3. \end{align*}$$

Ili kujibu swali la jinsi kanuni za kiasi cha viwango tofauti vya kawaida kama vile nyanja, koni, au silinda zinapatikana, tunataka kuonyesha mfano na kupata kiasi cha koni ya kiholela.

Mfano$\PageIndex{5B}$: Finding a Volume Using a Double Integral

Tumia viwianishi vya polar ili kupata kiasi ndani ya koni$z = 2 - \sqrt{x^2 + y^2}$ na juu ya$xy$ ndege.

Suluhisho

Mkoa$D$ wa ushirikiano ni msingi wa koni, ambayo inaonekana kuwa mduara kwenye$xy$ -ndege (Kielelezo$\PageIndex{10}$).

Kielelezo$\PageIndex{10}$: Kupata kiasi cha imara ndani ya koni na juu ya$xy$ -ndege.

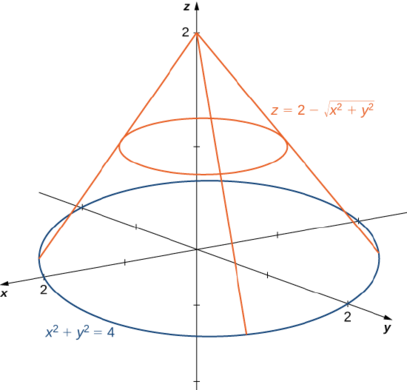
Tunapata equation ya mduara kwa kuweka$z = 0$:

$$\begin{align*} 0 &= 2 - \sqrt{x^2 + y^2} \\ 2 &= \sqrt{x^2 + y^2} \\ x^2 + y^2 &= 4. \end{align*}$$

Hii ina maana Radius ya mduara ni$2$ hivyo kwa ajili ya ushirikiano tuna$0 \leq \theta \leq 2\pi$ na$0 \leq r \leq 2$. Kubadilisha$x = r \, \cos \theta$ na$y = r \, \sin \, \theta$ katika equation$z = 2 - \sqrt{x^2 + y^2}$ tuliyo nayo$z = 2 - r$. Kwa hiyo, kiasi cha koni ni

$$\int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=2} (2 - r)\,r \, dr \, d\theta = 2 \pi \frac{4}{3} = \frac{8\pi}{3}\; \text{cubic units.} \nonumber$$

Uchambuzi

Kumbuka kwamba ikiwa tungepata kiasi cha koni ya kiholela na$\alpha$ vitengo vya radius na$h$ vitengo vya urefu, basi equation ya koni itakuwa$z = h - \frac{h}{a}\sqrt{x^2 + y^2}$.

Bado tunaweza kutumia Kielelezo$\PageIndex{10}$ na kuanzisha muhimu kama

$$\int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=a} \left(h - \frac{h}{a}r\right) r \, dr \, d\theta. \nonumber$$

Kutathmini muhimu, tunapata$\frac{1}{3} \pi a^2 h$.

Zoezi$\PageIndex{5}$

Matumizi kuratibu polar kupata muhimu iterated kwa ajili ya kutafuta kiasi cha imara iliyoambatanishwa na paraboloids$z = x^2 + y^2$ na$z = 16 - x^2 - y^2$.

Kidokezo

Sketching grafu inaweza kusaidia.

Jibu

$$V = \int_0^{2\pi} \int_0^{2\sqrt{2}} (16 - 2r^2) \,r \, dr \, d\theta = 64 \pi \; \text{cubic units.} \nonumber$$

Kama ilivyo na kuratibu mstatili, tunaweza pia kutumia viwianishi vya polar ili kupata maeneo ya mikoa fulani kwa kutumia mara mbili muhimu. Kama hapo awali, tunahitaji kuelewa eneo ambalo eneo tunataka kukokotoa. Kuchora grafu na kutambua kanda inaweza kusaidia kutambua mipaka ya ushirikiano. Kwa ujumla, formula ya eneo katika ushirikiano wa mara mbili itaonekana kama

$$\text{Area of} \, A = \int_{\alpha}^{\beta} \int_{h_1(\theta)}^{h_2(\theta)} 1 \,r \, dr \, d\theta. \nonumber$$

Mfano$\PageIndex{6A}$: Finding an Area Using a Double Integral in Polar Coordinates

Tathmini eneo lililofungwa na pembe$r = \cos \, 4\theta$.

Suluhisho

Kuchora grafu ya kazi$r = \cos \, 4\theta$ inaonyesha kuwa ni polar rose na petals nane (angalia takwimu zifuatazo).

Kielelezo$\PageIndex{11}$: Kutafuta eneo la polar rose na petals nane.

Kutumia ulinganifu, tunaweza kuona kwamba tunahitaji kupata eneo la petal moja na kisha kuzidisha kwa 8. Kumbuka kwamba maadili ambayo grafu hupita kupitia asili ni zero za kazi$\cos \, 4\theta$, na hizi ni nyingi isiyo ya kawaida ya$\pi/8$.$\theta$ Hivyo, moja ya petals inalingana na maadili$\theta$ ya wakati huo$[-\pi/8, \pi/8]$. Kwa hiyo, eneo imepakana na Curve$r = \cos \, 4\theta$ ni

$$\begin{align*} A &= 8 \int_{\theta=-\pi/8}^{\theta=\pi/8} \int_{r=0}^{r=\cos \, 4\theta} 1\,r \, dr \, d\theta \\ &= 8 \int_{\theta=-\pi/8}^{\theta=\pi/8}\left.\left[\frac{1}{2}r^2\right|_0^{\cos \, 4\theta}\right] d\theta \\ &= 8 \int_{-\pi/8}^{\pi/8} \frac{1}{2} \cos^24\theta \, d\theta \\&= 8\left. \left[\frac{1}{4} \theta + \frac{1}{16} \sin \, 4\theta \, \cos \, 4\theta \right|_{-\pi/8}^{\pi/8}\right] \\&= 8 \left[\frac{\pi}{16}\right] = \frac{\pi}{2}\; \text{units}^2. \end{align*}$$

Mfano$\PageIndex{6B}$: Finding Area Between Two Polar Curves

Pata eneo lililofungwa na mduara$r = 3 \, \cos \, \theta$ na cardioid$r = 1 + \cos \, \theta$.

Suluhisho

Kwanza kabisa, mchoro grafu za kanda (Kielelezo$\PageIndex{12}$).

Kielelezo$\PageIndex{12}$: Kutafuta eneo lililofungwa na mduara wote na cardioid.

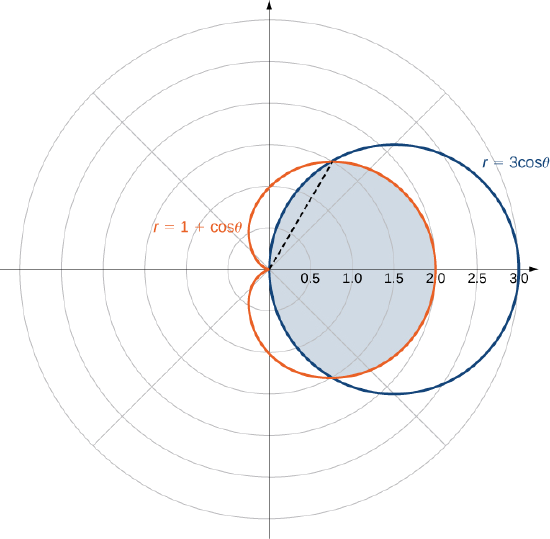
Tunaweza kuona ulinganifu wa grafu ambayo tunahitaji kupata pointi za makutano. Kuweka equations mbili sawa na kila mmoja anatoa

$$3 \, \cos \, \theta = 1 + \cos \, \theta. \nonumber$$

Moja ya pointi za makutano ni$\theta = \pi/3$. Eneo la juu ya mhimili wa polar lina sehemu mbili, na sehemu moja inavyoelezwa na cardioid kutoka$\theta = 0$ kwa$\theta = \pi/3$ na sehemu nyingine inayoelezwa na mduara kutoka$\theta = \pi/3$ kwa$\theta = \pi/2$. Kwa ulinganifu, eneo la jumla ni mara mbili eneo la juu ya mhimili wa polar. Hivyo, tuna

$$A = 2 \left[\int_{\theta=0}^{\theta=\pi/3} \int_{r=0}^{r=1+\cos \, \theta} 1 \,r \, dr \, d\theta + \int_{\theta=\pi/3}^{\theta=\pi/2} \int_{r=0}^{r=3 \, \cos \, \theta} 1\,r \, dr \, d\theta \right]. \nonumber$$

Kutathmini kila kipande tofauti, tunaona kwamba eneo hilo ni

$$A = 2 \left(\frac{1}{4}\pi + \frac{9}{16} \sqrt{3} + \frac{3}{8} \pi - \frac{9}{16} \sqrt{3} \right) = 2 \left(\frac{5}{8}\pi\right) = \frac{5}{4}\pi \, \text{square units.} \nonumber$$

Zoezi$\PageIndex{6}$

Pata eneo lililofungwa ndani ya cardioid$r = 3 - 3 \, \sin \theta$ na nje ya cardioid$r = 1 + \sin \theta$.

Kidokezo

Mchoro grafu, na usuluhishe kwa pointi za makutano.

Jibu

$$A = 2 \int_{-\pi/2}^{\pi/6} \int_{1+\sin \, \theta}^{3-3\sin \, \theta} \,r \, dr \, d\theta = \left(8 \pi + 9 \sqrt{3}\right) \; \text{units}^2 \nonumber$$

Mfano$\PageIndex{7}$: Evaluating an Improper Double Integral in Polar Coordinates

Tathmini muhimu

$$\iint_{R^2} e^{-10(x^2+y^2)} \,dx \, dy. \nonumber$$

Suluhisho

Hii ni muhimu yasiyofaa kwa sababu sisi ni kuunganisha juu ya mkoa unbounded$R^2$. Katika kuratibu polar, ndege nzima$R^2$ inaweza kuonekana kama$0 \leq \theta \leq 2\pi, \, 0 \leq r \leq \infty$.

Kutumia mabadiliko ya vigezo kutoka kuratibu mstatili kwa kuratibu polar, tuna

$$\begin{align*} \iint_{R^2} e^{-10(x^2+y^2)}\,dx \, dy &= \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=\infty} e^{-10r^2}\,r \, dr \, d\theta = \int_{\theta=0}^{\theta=2\pi} \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) d\theta \\ &=\left(\int_{\theta=0}^{\theta=2\pi}\right) d\theta \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) \\ &=2\pi \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) \\ &=2\pi \lim_{a\rightarrow\infty}\left(-\frac{1}{20}\right)\left(\left. e^{-10r^2}\right|_0^a\right) \\ &=2\pi \left(-\frac{1}{20}\right)\lim_{a\rightarrow\infty}\left(e^{-10a^2} - 1\right) \\ &= \frac{\pi}{10}. \end{align*}$$

Zoezi$\PageIndex{7}$

Tathmini muhimu

$$\iint_{R^2} e^{-4(x^2+y^2)}dx \, dy. \nonumber$$

Kidokezo

Badilisha kwenye mfumo wa kuratibu polar.

Jibu

$\frac{\pi}{4}$

Dhana muhimu

• Ili kuomba muhimu mara mbili kwa hali na ulinganifu wa mviringo, mara nyingi ni rahisi kutumia mara mbili muhimu katika kuratibu za polar. Tunaweza kutumia integrals hizi mbili juu ya mkoa polar mstatili au jumla eneo polar, kwa kutumia muhimu iterated sawa na wale kutumika kwa integrals mstatili mara mbili.
• Eneo$dA$ la kuratibu polar linakuwa$r \, dr \, d\theta$.
• Matumizi$x = r \, \cos \, \theta, \, y = r \, \sin \, \theta$, na$dA = r \, dr \, d\theta$ kubadili muhimu katika kuratibu mstatili kwa muhimu katika kuratibu polar.
• Tumia$r^2 = x^2 + y^2$ na$\theta = tan^{-1} \left(\frac{y}{x}\right)$ kubadili muhimu katika kuratibu za polar kwa muhimu katika kuratibu za mstatili, ikiwa inahitajika.
• Ili kupata kiasi katika viwianishi vya polar vilivyofungwa hapo juu na uso$z = f(r, \theta)$ juu ya kanda kwenye$xy$ -ndege, tumia sehemu mbili katika kuratibu za polar.

Mlinganyo muhimu

• Mara mbili muhimu juu ya mkoa wa mstatili wa polar$R$

$$\iint_R f(r, \theta) dA = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) \Delta A = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^nf(r_{ij}^*,\theta_{ij}^*)r_{ij}^*\Delta r \Delta \theta \nonumber$$

• Double muhimu juu ya mkoa wa jumla wa polar

$$\iint_D f(r, \theta)\,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r_2(\theta)} f (r,\theta) \,r \, dr \, d\theta \nonumber$$

faharasa

mstatili wa polar

kanda iliyoambatanishwa kati ya miduara$r = a$$r = b$ na pembe$\theta = \alpha$ na$\theta = \beta$; ni ilivyoelezwa kama$R = \{(r, \theta)\,|\,a \leq r \leq b, \, \alpha \leq \theta \leq \beta\}$