12.4: Bidhaa ya Msalaba
- Page ID
- 178125
- Tumia bidhaa ya msalaba wa vectors mbili zilizopewa.
- Tumia maamuzi ya kuhesabu bidhaa ya msalaba.
- Kupata vector orthogonal kwa wadudu wawili kupewa.
- Kuamua maeneo na kiasi kwa kutumia bidhaa msalaba.
- Tumia wakati wa nguvu iliyotolewa na vector msimamo.
Fikiria fundi akigeuka wrench ili kuimarisha bolt. Mechanic inatumia nguvu mwishoni mwa wrench. Hii inajenga mzunguko, au wakati, ambayo inaimarisha bolt. Tunaweza kutumia vectors kuwakilisha nguvu inayotumiwa na fundi, na umbali (radius) kutoka bolt hadi mwisho wa wrench. Kisha, tunaweza kuwakilisha moment na vector oriented pamoja mhimili wa mzunguko. Kumbuka kuwa vector ya wakati ni orthogonal kwa vector nguvu na vector radius.
Katika sehemu hii, tunaendeleza operesheni inayoitwa bidhaa ya msalaba, ambayo inatuwezesha kupata vector orthogonal kwa vectors mbili zilizopewa. Kuhesabu wakati ni matumizi muhimu ya bidhaa za msalaba, na tunachunguza wakati kwa undani zaidi baadaye katika sehemu hiyo.
Bidhaa ya Msalaba na Mali Zake
Bidhaa ya dot ni kuzidisha kwa wadudu wawili ambao husababisha scalar. Katika sehemu hii, tunaanzisha bidhaa ya vectors mbili zinazozalisha vector tatu orthogonal kwa mbili za kwanza. Fikiria jinsi tunaweza kupata vector vile. Hebu\(\vecs u=⟨u_1,u_2,u_3⟩\) na\(\vecs v=⟨v_1,v_2,v_3⟩\) uwe vectors zisizo za sifuri. Tunataka kupata\(\vecs w=⟨w_1,w_2,w_3⟩\) orthogonal vector kwa wote\(\vecs u\) na\(\vecs v\) - yaani, tunataka kupata\(\vecs w\) vile kwamba\(\vecs u ⋅ \vecs w=0\) na\( \vecs v⋅ \vecs w=0\). Kwa hiyo\(w_1\),\(w_2,\) na\(w_3\) lazima kukidhi
\[u_1w_1+u_2w_2+u_3w_3=0 \label{eq1} \]
\[v_1w_1+v_2w_2+v_3w_3=0. \label{eq2} \]
Kama sisi kuzidisha equation juu\(v_3\) na equation chini\(u_3\) na na Ondoa, tunaweza kuondoa variable\(w_3\), ambayo inatoa
\[(u_1v_3−v_1u_3)w_1+(u_2v_3−v_2u_3)w_2=0. \nonumber \]
Kama sisi kuchagua
\[\begin{align*} w_1 &=u_2v_3−u_3v_2 \\[4pt] w_2 &=−(u_1v_3−u_3v_1), \end{align*}\]
tunapata vector iwezekanavyo ufumbuzi. Kubadilisha maadili haya nyuma katika milinganyo ya awali (Equations\ ref {eq1} na\ ref {eq2}) inatoa
\[w_3=u_1v_2−u_2v_1. \nonumber \]
Hiyo ni, vector
\[\vecs w=⟨u_2v_3−u_3v_2,−(u_1v_3−u_3v_1),u_1v_2−u_2v_1⟩ \nonumber \]
ni orthogonal kwa wote\(\vecs u\) na\(\vecs v\), ambayo inatuongoza kufafanua operesheni ifuatayo, inayoitwa bidhaa ya msalaba.
Hebu\(\vecs u=⟨u_1,u_2,u_3⟩\) na\(\vecs v=⟨v_1,v_2,v_3⟩.\) Kisha, bidhaa ya msalaba\(\vecs u×\vecs v\) ni vector
\[\begin{align} \vecs u×\vecs v &= (u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1) \mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k} \nonumber \\[4pt] &=⟨u_2v_3−u_3v_2,−(u_1v_3−u_3v_1),u_1v_2−u_2v_1⟩. \label{cross}\end{align} \]
Kutoka kwa njia tuliyoendeleza\(\vecs u×\vecs v\), ni lazima iwe wazi kwamba bidhaa ya msalaba ni orthogonal kwa wote\(\vecs u\) na\(\vecs v\). Hata hivyo, kamwe huumiza kuangalia. Kuonyesha kwamba\(\vecs u×\vecs v\) ni orthogonal kwa\(\vecs u\), sisi mahesabu ya bidhaa dot ya\(\vecs u\) na\(\vecs u×\vecs v\).
\\ kuanza {align*}\ vecs u(\ vecs u×\ vecs v) &=u_1, u_2, u_3u_2v_3,1u_3v_2, -u_1v_3+u_3v_1, u_1v_2,1v_1\\ [4pt] &=u_3v_1, u_1v_2,1v_1 1 (u_2v_3,1u_3v_2) +u_2 (-u_1v_3+u_3v_1) +u_3 (u_1v_2,1u_2v_1)\\ [4pt]
&=u_1u_2v_3:u_1u_3v_2u_3+u_3+u_3+u _2u_3v_1+u_1u_3v_2,1u_2u_3v_1\\ [4pt]
& =( u_1u_2v_3—u_1u_2 v_3) + (-u_1u_3v_2+u_1u_3v_2) + (u_2u_3v_1,1-u_2u_3v_1)\\ [4pt]
&= 0\ mwisho {align*}\]
Kwa namna hiyo, tunaweza kuonyesha kwamba bidhaa ya msalaba pia ni ya kawaida\(\vecs v\).
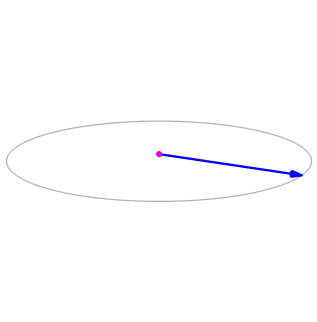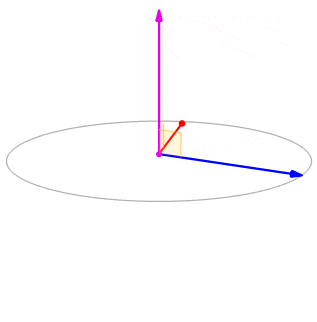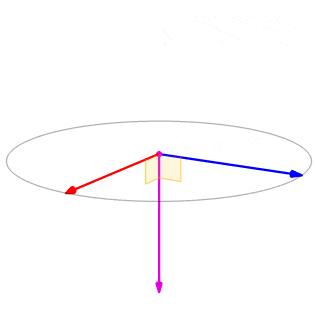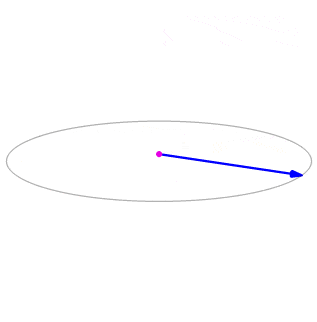
Hebu\(\vecs p=⟨−1,2,5⟩\) na\(\vecs q=⟨4,0,−3⟩\) (Kielelezo\(\PageIndex{1}\)). Kupata\(\vecs p×\vecs q\).
Suluhisho
Badilisha vipengele vya wadudu katika Equation\ ref {msalaba}:
\[\begin{align*} \vecs p×\vecs q &=⟨−1,2,5⟩×⟨4,0,−3⟩ \\[4pt] &= ⟨p_2q_3−p_3q_2,-(p_1q_3−p_3q_1),p_1q_2−p_2q_1⟩ \\[4pt] &= ⟨2(−3)−5(0),−(−1)(−3)+5(4),(−1)(0)−2(4)⟩ \\[4pt] &= ⟨−6,17,−8⟩.\end{align*}\]
Kupata\(\vecs p×\vecs q\) kwa\(\vecs p=⟨5,1,2⟩\) na\(\vecs q=⟨−2,0,1⟩.\) Express jibu kwa kutumia kiwango kitengo wadudu.
- Kidokezo
-
Tumia formula\(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k}.\)
- Jibu
-
\(\vecs p×\vecs q = \mathbf{\hat i}−9\mathbf{\hat j}+2\mathbf{\hat k}\)
Ingawa inaweza kuwa dhahiri kutoka kwa Equation\ ref {msalaba}, mwelekeo wa\(\vecs u×\vecs v\) unatolewa na utawala wa mkono wa kulia. Kama sisi kushikilia mkono wa kulia nje na vidole akizungumzia katika mwelekeo wa\(\vecs u\), kisha curl vidole kuelekea vector\(\vecs v\), pointi thumb katika mwelekeo wa bidhaa msalaba, kama inavyoonekana katika Kielelezo\(\PageIndex{2}\).
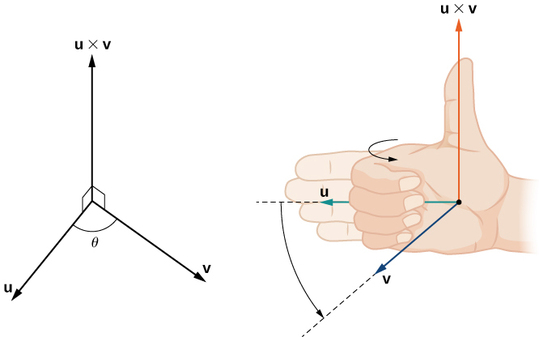
Angalia nini hii ina maana kwa ajili ya mwelekeo wa\(\vecs v×\vecs u\). Ikiwa tunatumia utawala wa mkono wa kulia\(\vecs v×\vecs u\), tunaanza na vidole vyetu vilivyoelekezwa kwenye mwelekeo wa\(\vecs v\), kisha pindua vidole vyetu kuelekea vector\(\vecs u\). Katika kesi hii, pointi thumb katika mwelekeo kinyume cha\(\vecs u×\vecs v\). (Jaribu!)
Hebu\(\vecs u=⟨0,2,1⟩\) na\(\vecs v=⟨3,−1,0⟩\). Tumia\(\vecs u×\vecs v\)\(\vecs v×\vecs u\) na uwape grafu.
Suluhisho
Tuna
\(\vecs u×\vecs v=⟨(0+1),−(0−3),(0−6)⟩=⟨1,3,−6⟩\)
\(\vecs v×\vecs u=⟨(−1−0),−(3−0),(6−0)⟩=⟨−1,−3,6⟩.\)
Tunaona kwamba, katika kesi hii,\(\vecs u×\vecs v=−(\vecs v×\vecs u)\) (Kielelezo\(\PageIndex{4}\)). Tunathibitisha hili kwa ujumla baadaye katika sehemu hii.
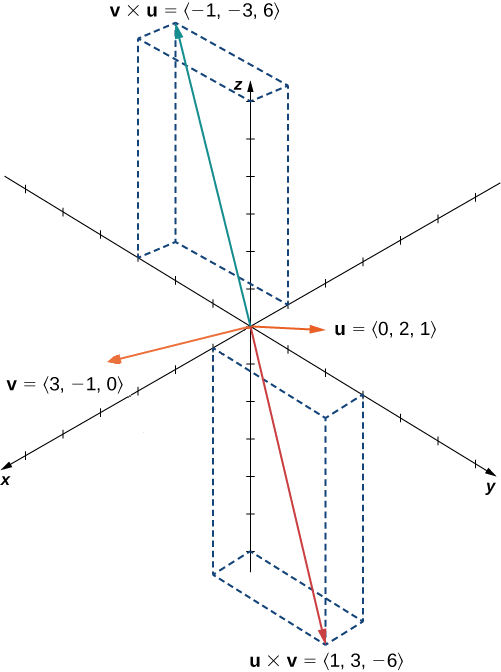
Kielelezo\(\PageIndex{4}\): Bidhaa za msalaba\(\vecs{u}×\vecs{v}\) na wote\(\vecs{v}×\vecs{u}\) ni orthogonal\(\vecs{u}\) na\(\vecs{v}\), lakini kwa njia tofauti.
Tuseme vectors\(\vecs u\) na\(\vecs v\) uongo katika\(xy\) -ndege (\(z\)sehemu ya kila vector ni sifuri). Sasa tuseme\(x\) - na\(y\) -vipengele vya\(\vecs u\) na\(y\) -sehemu ya wote\(\vecs v\) ni chanya, wakati\(x\) -sehemu ya\(\vecs v\) ni hasi. Kutokana na axes kuratibu ni oriented katika nafasi ya kawaida, katika mwelekeo gani haina\(\vecs u×\vecs v\) uhakika?
- Kidokezo
-
Kumbuka utawala wa mkono wa kulia (Kielelezo\(\PageIndex{2}\)).
- Jibu
-
Up (chanya\(z\) -mwelekeo)
Bidhaa za msalaba wa vectors ya kitengo cha kawaida\(\mathbf{\hat i}\),\(\mathbf{\hat j}\), na\(\mathbf{\hat k}\) inaweza kuwa na manufaa kwa kurahisisha mahesabu fulani, basi hebu tuchunguze bidhaa hizi za msalaba. Matumizi ya moja kwa moja ya ufafanuzi inaonyesha kwamba
\[\mathbf{\hat i}×\mathbf{\hat i}=\mathbf{\hat j}×\mathbf{\hat j}=\mathbf{\hat k}×\mathbf{\hat k}=\vecs 0. \nonumber \]
(Bidhaa ya msalaba wa vectors mbili ni vector, hivyo kila moja ya bidhaa hizi husababisha vector sifuri, si scalar\(0\).) Ni juu yako kuthibitisha mahesabu peke yako.
Zaidi ya hayo, kwa sababu bidhaa msalaba wa wadudu wawili ni orthogonal kwa kila moja ya wadudu hawa, tunajua kwamba bidhaa msalaba wa\(\mathbf{\hat i}\) na\(\mathbf{\hat j}\) ni sambamba na\(\mathbf{\hat k}\). Vile vile, bidhaa vector ya\(\mathbf{\hat i}\) na\(\mathbf{\hat k}\) ni sambamba na\(\mathbf{\hat j}\), na bidhaa vector ya\(\mathbf{\hat j}\) na\(\mathbf{\hat k}\) ni sambamba na\(\mathbf{\hat i}\).
Tunaweza kutumia utawala wa mkono wa kulia ili kuamua mwelekeo wa kila bidhaa. Kisha tuna
\ [kuanza {align*}\ mathbf {\ kofia i} ×\ hatbf {\ kofia j} &=\ mathbf {\ kofia k}\\ [4pt]
\ mathbf {\ kofia j} ×\ mathbf {\ kofia i} &=|\ hatbf {\ kofia k}\\ [10pt]
\ mathbf\\ kofia j} ×\ mathbf {\ kofia k} &=\ mathbf {\ kofia i}\\ [4pt]
\ mathbf {\ kofia k} ×\ hatbf {\ kofia j} &=\ mathbf {\ kofia i}\\ [10 pt]
\ mathbf {\ kofia k} ×\ mathbf {\ kofia i} &=\ mathbf {\ kofia j}\\ [4pt]
\ mathbf {\ kofia i} ×\ hatbf {\ kofia k} &=\ mathbf {\ kofia j}. \ mwisho {align*}\]
Njia hizi zinakuja kwa manufaa baadaye.
Kupata\(\mathbf{\hat i} ×(\mathbf{\hat j}×\mathbf{\hat k})\).
Suluhisho
Tunajua kwamba\(\mathbf{\hat j}×\mathbf{\hat k}=\mathbf{\hat i}\). Kwa hiyo,\(\mathbf{\hat i}×(\mathbf{\hat j}×\mathbf{\hat k})=\mathbf{\hat i}×\mathbf{\hat i}=\vecs 0.\)
Kupata\((\mathbf{\hat i}×\mathbf{\hat j})×(\mathbf{\hat k}×\mathbf{\hat i}).\)
- Kidokezo
-
Kumbuka utawala wa mkono wa kulia (Kielelezo\(\PageIndex{2}\)).
- Jibu
-
\(−\mathbf{\hat i}\)
Kama tulivyoona, bidhaa ya dot mara nyingi huitwa bidhaa ya scalar kwa sababu inasababisha scalar. Bidhaa ya msalaba husababisha vector, hivyo wakati mwingine huitwa bidhaa ya vector. Shughuli hizi ni matoleo yote ya kuzidisha vector, lakini wana mali tofauti na programu. Hebu tuchunguze baadhi ya mali ya bidhaa ya msalaba. Sisi kuthibitisha tu wachache wao. Ushahidi wa mali nyingine huachwa kama mazoezi.
Hebu\(\vecs u,\vecs v,\) na\(\vecs w\) uwe wadudu katika nafasi, na uache\(c\) kuwa scalar.
- Mali isiyohamishika:\[\vecs u×\vecs v=−(\vecs v×\vecs u) \nonumber \]
- Mali ya usambazaji:\[\vecs u×(\vecs v+\vecs w)=\vecs u×\vecs v+\vecs u×\vecs w \nonumber \]
- Kuzidisha kwa mara kwa mara:\[c(\vecs u×\vecs v)=(c\vecs u)×\vecs v=\vecs u×(c\vecs v) \nonumber \]
- Bidhaa ya msalaba wa vector sifuri:\[\vecs u×\vecs 0=\vecs 0×\vecs u=\vecs 0 \nonumber \]
- Bidhaa ya msalaba wa vector yenyewe:\[\vecs v×\vecs v=\vecs 0 \nonumber \]
- Scalar bidhaa tatu:\[\vecs u⋅(\vecs v×\vecs w)=(\vecs u×\vecs v)⋅\vecs w \nonumber \]
Kwa ajili ya mali\(i\), tunataka kuonyesha\(\vecs u×\vecs v=−(\vecs v×\vecs u).\) Tuna
\[\begin{align*} \vecs u×\vecs v &=⟨u_1,u_2,u_3⟩×⟨v_1,v_2,v_3⟩ \\[4pt] &=⟨u_2v_3−u_3v_2,−u_1v_3+u_3v_1,u_1v_2−u_2v_1⟩ \\[4pt] &=−⟨u_3v_2−u_2v_3,−u_3v_1+u_1v_3,u_2v_1−u_1v_2⟩ \\[4pt] &=−⟨v_1,v_2,v_3⟩×⟨u_1,u_2,u_3⟩\\[4pt] &=−(\vecs v×\vecs u).\end{align*}\]
Tofauti na shughuli nyingi tumeona, bidhaa msalaba si commutative. Hii ina maana ikiwa tunafikiri juu ya utawala wa mkono wa kulia.
Kwa mali\(iv\)., hii ifuatavyo moja kwa moja kutoka ufafanuzi wa bidhaa msalaba. Tuna
\[\vecs u × \vecs 0=⟨u_2(0)−u_3(0),−(u_1(0)−u_3(0)),u_1(0)−u_2(0)⟩=⟨0,0,0⟩=\vecs 0. \nonumber \]
Kisha, kwa mali i.,\(\vecs 0×\vecs u=\vecs 0\) pia. Kumbuka kwamba bidhaa ya dot ya vector na vector sifuri ni scalar\(0\), wakati bidhaa msalaba wa vector na vector sifuri ni vector\(\vecs 0\).
\(vi\)Mali. inaonekana kama mali associative, lakini kumbuka mabadiliko katika shughuli:
\ [kuanza {align*}\ vecs u(\ vecs v×\ vecs w) &=uv_2w_3,1v_3w_2, -v_1w_3+v_3w_1, v_1w_2,1v_2w_1cus\\ [4pt]
&= u_1 (v_2w_3,1v_3,1v_3,1v_3,1v_3:v_3,1v_3:v_3:v_3w w_2) +u_2 (-v_1w_3+v_3w_1) +u_3 (v_1w_2,1v_2w_1)\\ [4pt]
&=u_1v_2w_3:u_1v_3w_1v_3w_1+u_3w_1+u_3w_1+u_3w_1+u_3w_1+u_3w_1+u_3w_1+u_3w_1+u_3w_1+u_3w_1+v_1w_2,1u_3v_2w_1\\ [4pt]
& =( u_2v_3:u_3:u_3v _2) w_1+ (u_3v_1,1-u_1v_3) w_2+ (u_1v_2,1u_2v_1) w_3\\ [4pt]
&=u_2v_3,1u_3v_2, u_3v_1,1u_1v_3, u_1v_2v_1v_3, u_1v_2v_1v_3 w_1, w_2, w_3=(\ vecs u×\ vecs v)\ vecs w.\ mwisho {align*}\]
\(\square\)
Tumia mali za bidhaa za msalaba ili uhesabu\((2\mathbf{\hat i}×3\mathbf{\hat j})×\mathbf{\hat j}.\)
Suluhisho
\ [kuanza {align*} (2\ mathbf {\ kofia i} × 3\ hatbf {\ kofia j}) ×\ mathbf {\ kofia j} &=2 (\ mathbf {\ kofia i} × 3\ hatbf {\ kofia j}) ×\ hatbf {\ kofia j}\\ [4pt]
&=2 (3) (\ mathbf {\ kofia i} ×\ mathbf {\ kofia j}) ×\ mathbf {\ kofia j}\\ [4pt]
& =( 6\ mathbf {\ kofia k}) ×\ mathbf {\ kofia j}\\ [4pt]
&=6 (\ mathbf { \ kofia k} ×\ mathbf {\ kofia j})\\ [4pt]
&=6 (-\ mathbf {\ kofia i}) =-6\ mathbf {\ kofia i}. \ mwisho {align*}\]
Tumia mali ya bidhaa ya msalaba ili uhesabu\((\mathbf{\hat i}×\mathbf{\hat k})×(\mathbf{\hat k}×\mathbf{\hat j}).\)
- Kidokezo
-
\(\vecs u×\vecs v=−(\vecs v×\vecs u)\)
- Jibu
-
\(−\mathbf{\hat k}\)
Hadi sasa katika sehemu hii, tumekuwa na wasiwasi na mwelekeo wa vector\(\vecs u×\vecs v\), lakini hatujajadili ukubwa wake. Inageuka kuna kujieleza rahisi kwa ukubwa wa\(\vecs u×\vecs v\) kuwashirikisha ukubwa wa\(\vecs u\) na\(\vecs v\), na sine ya angle kati yao.
Hebu\(\vecs u\) na\(\vecs v\) kuwa vectors, na basi\(θ\) iwe angle kati yao. Kisha,\(‖\vecs u×\vecs v‖=‖\vecs u‖⋅‖\vecs v‖⋅\sin θ.\)
Hebu\(\vecs u=⟨u_1,u_2,u_3⟩\) na\(\vecs v=⟨v_1,v_2,v_3⟩\) uwe wadudu, na hebu\(θ\) ueleze angle kati yao. Kisha
\ [kuanza {align*}}\ vecs u×\ vecs v^2 &= (u_2v_3:u_3v_3v_2) ^2+ (u_3v_1,1-u_1v_3) ^2+ (u_1v_2,1u_2v_1) ^2\\ [4pt]
&=u^2_2v^2_2v^2_3_1) ^2\\ [4pt] &=u ^ 2_2v^2_3v_1 -2u_2u_3v_2v_3+u ^ 2_3v^2_2+u ^ 2_3v^2_3v^2_1u_1u_3v_3+u ^
2_1v^2_3+u ^ 2_1v^2_1v^2_2v^2_2v^2_1\\ [4pt] &=u ^ 2_1v^2_1+u ^ 2_1v^2_2+u ^ 2_1v^2_1v^2_2v^2_1+u ^ 2_1+u ^ 2_2v ^2_2+u ^ 2_2v^2_3+u ^ 2_3v^2_1+u ^ 2_3v^2_2+u ^ 2_3v^2_3v^2_3v^2_1v^2_1+u ^ 2_2v^2_2+u ^ 2_3v^2_3v_2u_2v_1v_1v_1v_1 2+2u_1u_3v_1v_3+2u_2u_3v_2v_3)\\ [4pt]
& =( u ^ 2_1+u ^ 2_2+u ^ 2_3) (v^2_1+v ^ 2_2+v ^ 2_3) - (u_1v_1+u_2v_2+u_3v_2+u_3v_2+_3) ^2\\ [4pt]
&=\ vecs u^2vecs\ vecs v^2 - (\ vecs u\ vecs v) ^2\\ [4pt]
&=\ vecs u^2\ vecs v^2,1cs u^2:00\ vecs v^2\ cos^2\ [4pt]
&=// vecs u^2vecs v^2 (1 -\\ cos^2)\ [4pt]
&=\ vecs u^ 2\ vecs vecs 2\\ vecs vecs v^ 2\\ vecs vecs ^2 (\ dhambi ^2). \ mwisho {align*}\ nonumber\]
Kuchukua mizizi ya mraba na kutambua kwamba\(\sqrt{\sin^2θ}=\sinθ\) kwa\(0≤θ≤180°,\) tuna matokeo yaliyohitajika:
\[‖\vecs u×\vecs v‖=‖\vecs u‖‖\vecs v‖ \sin θ. \nonumber \]
□
Ufafanuzi huu wa bidhaa ya msalaba inatuwezesha kutazama au kutafsiri bidhaa kijiometri. Ni wazi, kwa mfano, kwamba bidhaa ya msalaba hufafanuliwa tu kwa vectors katika vipimo vitatu, si kwa vectors katika vipimo viwili. Katika vipimo viwili, haiwezekani kuzalisha vector wakati huo huo orthogonal kwa vectors mbili zisizo sawa.
Tumia “Ukubwa wa Bidhaa ya Msalaba” ili kupata ukubwa wa bidhaa za msalaba\(\vecs u=⟨0,4,0⟩\) na\(\vecs v=⟨0,0,−3⟩\).
Suluhisho
Tuna
\ [kuanza {align*}}\ vecs u×\ vecs vecs vecs\\ vecs vν\\ sin\ [4pt]
&=\ sqrt {0 ^ 2+4^2+0^2}}}\ sqrt {0 ^2+0^2+ (1-3) ^2}}}\ dhambi {\ dfrac {π} {0 ^ 2+0} 2}}\\ [4pt]
&=4 (3) (1) =12\ mwisho {align*}\]
Tumia “Ukubwa wa Bidhaa ya Msalaba” ili kupata ukubwa wa\(\vecs u×\vecs v\), wapi\(\vecs u=⟨−8,0,0⟩\) na\(\vecs v=⟨0,2,0⟩\).
- Kidokezo
-
Vectors\(\vecs u\) na\(\vecs v\) ni orthogonal.
- Jibu
-
16
Vigezo na Bidhaa ya Msalaba
Kutumia Equation\ ref {msalaba} kupata bidhaa msalaba wa wadudu wawili ni moja kwa moja, na inatoa bidhaa msalaba katika fomu muhimu sehemu. Fomu, hata hivyo, ni ngumu na vigumu kukumbuka. Kwa bahati nzuri, tuna mbadala. Tunaweza kuhesabu bidhaa ya msalaba wa vectors mbili kwa kutumia notation determinant.
\(2×2\)Determinant inaelezwa na
\[\begin{vmatrix}a_1 & b_1\\a_2 & b_2\end{vmatrix} =a_1b_2−b_1a_2. \nonumber \]
Kwa mfano,
\[\begin{vmatrix}3 & −2\\5 & 1\end{vmatrix} =3(1)−5(−2)=3+10=13. \nonumber \]
\(3×3\)Determinant inaelezwa kwa suala la\(2×2\) kuamua kama ifuatavyo:
\[\begin{vmatrix}a_1 & a_2 & a_3\\b_1 & b_2 & b_3\\c_1 & c_2 & c_3\end{vmatrix}=a_1\begin{vmatrix}b_2 & b_3\\c_2 & c_3\end{vmatrix}−a_2\begin{vmatrix}b_1 & b_3\\c_1 & c_3\end{vmatrix}+a_3\begin{vmatrix}b_1 & b_2\\c_1 & c_2\end{vmatrix}.\label{expandEqn} \]
Equation\ ref {ExpandeQN} inajulikana kama upanuzi wa determinant kando ya mstari wa kwanza. Kumbuka kwamba multipliers ya kila moja ya\(2×2\) determinants upande wa kulia wa maneno haya ni entries katika mstari wa kwanza wa\(3×3\) kuamua. Zaidi ya hayo, kila moja ya\(2×2\) determinants ina entries kutoka\(3×3\) determinant kwamba ingekuwa kubaki kama shilingi nje mstari na safu zenye multiplier. Hivyo, kwa muda wa kwanza upande wa kulia,\(a_1\) ni multiplier, na\(2×2\) determinant ina entries kwamba kubaki kama wewe kuvuka nje mstari wa kwanza na safu ya kwanza ya\(3×3\) determinant. Vile vile, kwa muda wa pili, mchezaji ni\(a_2\), na\(2×2\) uamuzi una maingizo yaliyobaki ikiwa unavuka mstari wa kwanza na safu ya pili ya\(3×3\) uamuzi. Angalia, hata hivyo, kwamba mgawo wa muda wa pili ni hasi. Neno la tatu linaweza kuhesabiwa kwa mtindo sawa.
Tathmini ya kuamua\(\begin{vmatrix}2 & 5 &−1\\−1 & 1 & 3\\−2 & 3 & 4\end{vmatrix}\).
Suluhisho
Tuna
\ [kuanza {align*}\ kuanza {vmatrix} 2 & 5 & -1\\ -1 & 1 & 3\ uundaji 3 & 4\ mwisho {vmatrix} &= 2\ kuanza {vmatrix} 1 & 3\\ 3 & 4\ mwisho {vmatrix} -5\ kuanza {vmatrix} -1\ kuanza {vmatrix} -1\ kuanza {vmatrix} -1\ matrix} -1 & 1\\ -1 & 3\ mwisho {vmatrix}\\ [4pt]
&= 2 (4-9) -5 (-4+6) -1 (-3+2 )\\ [4pt]
&= 2 (-5) -5 (2) -1 (-1) =-10,1+1\\ [4pt]
&=,119\ mwisho {align*}\]
Tathmini ya kuamua\(\begin{vmatrix}1 & −2 & −1\\3 & 2 & −3\\1 & 5 & 4\end{vmatrix}\).
- Kidokezo
-
Panua kando ya mstari wa kwanza. Usisahau muda wa pili ni hasi!
- Jibu
-
40
Kitaalam, uamuzi hufafanuliwa tu kwa suala la safu za idadi halisi. Hata hivyo, notation ya kuamua hutoa kifaa muhimu cha mnemonic kwa formula ya bidhaa za msalaba.
Hebu\(\vecs u=⟨u_1,u_2,u_3⟩\) na\(\vecs v=⟨v_1,v_2,v_3⟩\) uwe wadudu. Kisha bidhaa ya msalaba\(\vecs u×\vecs v\) hutolewa na
\[\vecs u×\vecs v=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\u_1 & u_2 & u_3\\v_1 & v_2 & v_3\end{vmatrix}=\begin{vmatrix}u_2 & u_3\\v_2 & v_3\end{vmatrix}\mathbf{\hat i}−\begin{vmatrix}u_1 & u_3\\v_1 & v_3\end{vmatrix}\mathbf{\hat j}+\begin{vmatrix}u_1 & u_2\\v_1 & v_2\end{vmatrix}\mathbf{\hat k}. \nonumber \]
Hebu\(\vecs p=⟨−1,2,5⟩\) na\(\vecs q=⟨4,0,−3⟩\). Kupata\(\vecs p×\vecs q\).
Suluhisho
Tunaanzisha uamuzi wetu kwa kuweka vectors ya kitengo cha kawaida\(\vecs u\) katika mstari wa kwanza, vipengele vya mstari wa pili, na vipengele vya\(\vecs v\) mstari wa tatu. Kisha, tuna
\ [kuanza {align*}\ vecs p×\ vecs q &=\ kuanza {vmatrix}\ hisabati {\ kofia i} &\ mathbf {\ kofia j} &\ mathbf {\ kofia k}\\ -1 & 2 & 5\ 4 & 0 & -3\ mwisho {vmatrix} =\ kuanza {vmatrix} 2 & 5\\ 0 & 3\ mwisho {vmatrix}\ mathbf {\ kofia i} -\ kuanza {vmatrix} -1 & 5\\ 4 & 1-3\ mwisho {vmatrix}\ matriki {\ kofia j} +\ kuanza {vmatrix} - 1 & 2\ 4 & 0\ mwisho {vmatrix}\ mathbf {\ kofia k}\\ [4pt]
&= (-6—0)\ mathbf {\ kofia i} - (3—20)\ mathbf {\ kofia j} + (0—8)\ mathbf {\ kofia k}\ [4pt] &=-6\ mathbf {\ kofia k}\ [4pt]
&=—6\ mathbf f {\ hat i} +17\ mathbf {\ kofia j} -8\ mathbf {\ kofia k}. \ mwisho {align*}\]
Kumbuka kwamba jibu hili linathibitisha hesabu ya bidhaa msalaba katika Mfano\(\PageIndex{1}\).
Tumia nukuu ya kuamua kupata\(\vecs a×\vecs b\), wapi\(\vecs a=⟨8,2,3⟩\) na\(\vecs b=⟨−1,0,4⟩.\)
- Kidokezo
-
Tumia maamuzi\(\begin{vmatrix}\mathbf{\hat i} \mathbf{\hat j} \mathbf{\hat k}\\8 & 2 & 3\\−1 & 0 & 4\end{vmatrix}\).
- Jibu
-
\(\vecs a×\vecs b = 8\mathbf{\hat i}−35\mathbf{\hat j}+2\mathbf{\hat k}\)
Kutumia Bidhaa ya Msalaba
Bidhaa ya msalaba ni muhimu sana kwa aina kadhaa za hesabu, ikiwa ni pamoja na kutafuta vector orthogonal kwa wadudu wawili waliopewa, maeneo ya kompyuta ya pembetatu na parallelograms, na hata kuamua kiasi cha sura tatu-dimensional kijiometri alifanya ya parallelograms inayojulikana kama parallelepiped. Mifano zifuatazo zinaonyesha mahesabu haya.
Hebu\(\vecs a=⟨5,2,−1⟩\) na\(\vecs b=⟨0,−1,4⟩\). Kupata kitengo vector orthogonal kwa wote\(\vecs a\) na\(\vecs b\).
Suluhisho
Bidhaa ya msalaba\(\vecs a×\vecs b\) ni orthogonal kwa wadudu wote\(\vecs a\) na\(\vecs b\). Tunaweza kuhesabu kwa kuamua:
\ [kuanza {align*}\ vecs a×\ vecs b &=\ kuanza {vmatrix}\ hisabati {\ kofia i} &\ mathbf {\ kofia j} &\ mathbf {\ kofia k}\\ 5 & 2 & -1\\ 0 & -1 & 4\ mwisho {vmatrix} =\ kuanza {vmatrix} 2 & -1\\ -1 & 4\ mwisho {vmatrix}\ matriki {\ kofia i} -\ kuanza {vmatrix} 5 & -1\\ 0 & 4\ mwisho {vmatrix}\ matriki {\ kofia j} +\ kuanza {vmatrix} 5 & 2\\ 0 & -1\ mwisho {vmatrix}\ mathbf {\ kofia k}\\ [4pt]
& = (8—1)\ mathbf {\ kofia i} - (20—0)\ mathbf {\ kofia j} + (-5—0)\ mathbf {\ kofia k}\ [4pt]
&=7\ mathbf {\ hat i} -20\ mathbf {\ kofia j} -5\ mathbf {\ kofia k}. \ mwisho {align*}\ nonumber\]
Weka vector hii ili kupata vector kitengo katika mwelekeo huo:
\(\|\vecs a×\vecs b\|=\sqrt{(7)^2+(−20)^2+(−5)^2}=\sqrt{474}\).
Hivyo,\(\left\langle\dfrac{7}{\sqrt{474}},\dfrac{−20}{\sqrt{474}},\dfrac{−5}{\sqrt{474}}\right\rangle\) ni kitengo vector orthogonal\(\vecs a\) na\(\vecs b\).
Rahisi, vector hii inakuwa\(\left\langle\dfrac{7\sqrt{474}}{474},\dfrac{−10\sqrt{474}}{237},\dfrac{−5\sqrt{474}}{474}\right\rangle\).
Kupata kitengo vector orthogonal kwa wote\(\vecs a\) na\(\vecs b\), wapi\(\vecs a=⟨4,0,3⟩\) na\(\vecs b=⟨1,1,4⟩.\)
- Kidokezo
-
Weka bidhaa ya msalaba.
- Jibu
-
\(\left\langle\dfrac{−3}{\sqrt{194}},\dfrac{−13}{\sqrt{194}},\dfrac{4}{\sqrt{194}}\right\rangle\)au, kilichorahisishwa kama\(\left\langle\dfrac{−3\sqrt{194}}{194},\dfrac{−13\sqrt{194}}{194},\dfrac{2\sqrt{194}}{97}\right\rangle\)
Ili kutumia bidhaa ya msalaba kwa ajili ya kuhesabu maeneo, tunasema na kuthibitisha theorem ifuatayo.
Ikiwa tunapata vectors\(\vecs u\) na\(\vecs v\) vile vile huunda pande za karibu za parallelogram, basi eneo la parallelogram hutolewa na\(‖\vecs u×\vecs v‖\) (Kielelezo\(\PageIndex{5}\)).
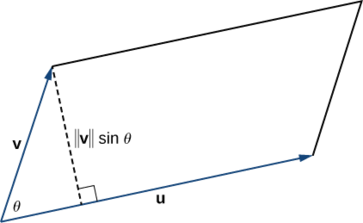
Tunaonyesha kwamba ukubwa wa bidhaa ya msalaba ni sawa na urefu wa nyakati za msingi wa parallelogram.
\[\begin{align*} \text{Area of a parallelogram} &= \text{base} × \text{height} \\[4pt] &=‖\vecs u‖(‖\vecs v‖\sin θ) \\[4pt] &=‖\vecs u×\vecs v‖ \end{align*}\]
□
Hebu\(P=(1,0,0),Q=(0,1,0),\) na\(R=(0,0,1)\) uwe na alama za pembetatu (Kielelezo\(\PageIndex{6}\)). Pata eneo lake.
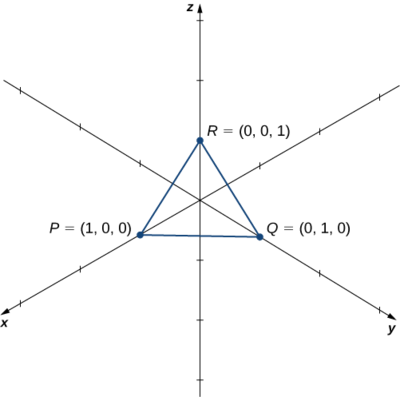
Suluhisho
Tuna\(\vecd{PQ}=⟨0−1,1−0,0−0⟩=⟨−1,1,0⟩\) na\(\vecd{PR}=⟨0−1,0−0,1−0⟩=⟨−1,0,1⟩\). Eneo la parallelogram na pande zilizo karibu\(\vecd{PQ}\) na\(\vecd{PR}\) hutolewa na\(∥\vecd{PQ}×\vecd{PR}∥\):
\ [kuanza {align*}\ vecd {PQ}\ mara\ vecd {PR} &=\ kuanza {vmatrix}\ matriki {\ kofia i} &\ mathbf {\ kofia j} &\ hatbf {\ kofia k}\\ -1 & 1 & 0 & 1\ mwisho {vmatrix}\\ [4pt]
&= (1-0)\ mathbf {\ kofia i} - (-1,1-0)\ mathbf {\ kofia j} + (0-1))\ mathbf {\ kofia k}\\ [4pt]
&=\ mathbf {\ kofia i} +\ mathbf {\ kofia j} +\ mathbf {\ kofia k}\\ [10pt]
\ vecd {PQ} ×\ vecd {PR} &=1,1\\ [4pt]
&=\\ sqrt {1 ^2+1^2}\\ [4pt]
&=\ sqrt {3}. \ mwisho {align*}\ nonumber\]
Eneo la\(ΔPQR\) nusu eneo la parallelogram au\(\sqrt{3}/2 \, \text{units}^2\).
Pata eneo la parallelogram\( PQRS\) na vertices\( P(1,1,0)\)\(Q(7,1,0)\),\(R(9,4,2)\),, na\( S(3,4,2)\).
- Kidokezo
-
Mchoro parallelogram na kutambua vectors mbili ambazo huunda pande karibu za parallelogram.
- Jibu
-
\(6\sqrt{13}\, \text{units}^2\)
Bidhaa ya Scalar Triple
Kwa sababu bidhaa ya msalaba wa vectors mbili ni vector, inawezekana kuchanganya bidhaa ya dot na bidhaa ya msalaba. Bidhaa ya dot ya vector yenye bidhaa ya msalaba wa vectors nyingine mbili inaitwa bidhaa tatu za scalar kwa sababu matokeo ni scalar.
mara tatu scalar bidhaa ya wadudu\( \vecs u\),\( \vecs v,\) na\(\vecs w\) ni
\[ \vecs u⋅( \vecs v× \vecs w). \nonumber \]
Bidhaa tatu za scalar ya vectors
\[ \vecs u=u_1 \mathbf{\hat i}+u_2 \mathbf{\hat j}+u_3\mathbf{\hat k} \nonumber \]
\[ \vecs v=v_1\mathbf{\hat i}+v_2\mathbf{\hat j}+v_3\mathbf{\hat k} \nonumber \]
na
\[ \vecs w=w_1 \mathbf{\hat i}+w_2\mathbf{\hat j}+w_3\mathbf{\hat k} \nonumber \]
ni uamuzi wa\(3×3\) tumbo lililoundwa na vipengele vya vectors:
\[ \vecs u⋅( \vecs v× \vecs w)=\begin{vmatrix}u_1 & u_2 & u_3\\v_1 & v_2 & v_3\\w_1 & w_2 & w_3\end{vmatrix}. \label{triple2} \]
Mahesabu ni moja kwa moja.
\ [kuanza {align*}\ vecs u(\ vecs v×\ vecs w) &=u_1, u_2, u_3v_2w_3,1v_3w_2, -v_1w_3+v_3w_1, v_1w_2,1v_2w_1cas\\ [4pt] &=u__3w_1, v_1w_1, v_1w_2w_1car\\ [4pt] &=u__3w_1, v_1w_2,1v_2w_1car\\ 1 (v_2w_3,1v_3w_2) +u_2 (-v_1w_3+v_3w_1) +u_3 (
v_1w_2,1v_2w_1)\\ [4pt] &=u_1 (v_2w_3,1v_3w_2) -u_2 (v_1w_3,1v_3,1v_3 _3w_1) +u_3 (v_1w_2-v_2w_1)\\ [4pt]
&=\ kuanza {vmatrix} u_ 1 & u_2 & u_3\\ v_1 & v_2 & v_3\\ w_1 & w_2 & w_3\ mwisho {vmatrix}. \ mwisho {align*}\ nonumber\]
□
Hebu\(\vecs u=⟨1,3,5⟩,\,\vecs v=⟨2,−1,0⟩\) na\(\vecs w=⟨−3,0,−1⟩\). Tumia bidhaa tatu za scalar\(\vecs u⋅(\vecs v×\vecs w).\)
Suluhisho
Weka Equation\ ref {triple2} moja kwa moja:
\ [kuanza {align*}\ vecs (\ vecs v×\ vecs w) &=\ kuanza {vmatrix} 1 & 3 & 5 & -1 & 1 & 1 & 0 & -1\ mwisho {vmatrix}\\ [4pt]
&= 1\ kuanza {vmatrix} -1 & 0\\ mwisho {vmatrix} -1\\ kuanza {vmatrix} 2 & 0\ 1-3 & -1\ mwisho {vmatrix} +5\ kuanza {vmatrix} 2 & -1\\ -3 & 0\ mwisho { matrix}\\ [4pt]
& = (1,10) -3 (-2,10) +5 (0,1-3)\\ [4pt]
&=1+6—15=-8. \ mwisho {align*}\ nonumber\]
Tumia bidhaa tatu za scalar\(\vecs a⋅(\vecs b×\vecs c),\) ambapo\(\vecs a=⟨2,−4,1⟩, \vecs b=⟨0,3,−1⟩\), na\(\vecs c=⟨5,−3,3⟩.\)
- Kidokezo
-
Weka vectors kama safu ya\(3×3\) tumbo, kisha uhesabu uamuzi.
- Jibu
-
\(17\)
Tunapounda tumbo kutoka kwa vectors tatu, lazima tuwe makini kuhusu utaratibu ambao tunaandika vectors. Ikiwa tunawaorodhesha kwenye tumbo kwa utaratibu mmoja na kisha upya safu, thamani kamili ya uamuzi bado haibadilika. Hata hivyo, kila wakati safu mbili zinabadilisha maeneo, mabadiliko ya kuamua ishara:
\(\begin{vmatrix}a_1 & a_2 & a_3\\b_1 & b_2 & b_3\\c_1 & c_2 & c_3\end{vmatrix}=d \quad\quad \begin{vmatrix}b_1 & b_2 & b_3\\a_1 & a_2 & a_3\\c_1 & c_2 & c_3\end{vmatrix}=−d \quad\quad \begin{vmatrix}b_1 & b_2 & b_3\\c_1 & c_2 & c_3\\a_1 & a_2 & a_3\end{vmatrix}=d \quad\quad \begin{vmatrix}c_1 & c_2 & c_3\\b_1 & b_2 & b_3\\a_1 & a_2 & a_3\end{vmatrix}=−d\)
Kuthibitisha ukweli huu ni moja kwa moja, lakini badala ya messy. Hebu tuangalie hili kwa mfano:
\ [kuanza {align*}\ kuanza {vmatrix} 1 & 2 & 1\\ -2 & 0 & 3\ 4 & 1 & -1\ mwisho {vmatrix} &=\ kuanza {vmatrix} 0 & 3\ 1 & -1\ mwisho {vmatrix} -1\ kuanza {vmatrix} -2 & 3\ 4 & -1\ mwisho {vmatrix} +\ kuanza {vmatrix}} -2 & 0\\ 4 & 1\ mwisho {vmatrix}\\ [4pt]
& = (0,13) -2 (2,112) + (-2,10)\\ [4pt]
&=-3+20,12=15. \ mwisho {align*}\ nonumber\]
Inabadilisha safu mbili za juu tunazo
\ [kuanza {align*}\ kuanza {vmatrix} -1 & 0 & 3\\ 1 & 1 & 1 & 1 & 1 & -1\ mwisho {vmatrix} &=-2\ kuanza {vmatrix} 2 & 1 & -1\\ mwisho {vmatrix} +3\ kuanza {vmatrix} 1 & 2\ 4 & 1\ mwisho {vmatrix}\\ [4pt]
&=-1 (-2,11) +3 (1,18)\\ [4pt]
&=6—21=,115. \ mwisho {align*}\ nonumber\]
Kupanga upya vectors katika bidhaa tatu ni sawa na kurekebisha safu katika tumbo la kuamua. Hebu\(\vecs u=u_1\mathbf{\hat i}+u_2\mathbf{\hat j}+u_3\mathbf{\hat k}, \vecs v=v_1\mathbf{\hat i}+v_2\mathbf{\hat j}+v_3\mathbf{\hat k},\) na\(\vecs w=w_1\mathbf{\hat i}+w_2\mathbf{\hat j}+w_3\mathbf{\hat k}.\) Kutumia Kumbuka, tuna
\[\vecs u⋅(\vecs v×\vecs w)=\begin{vmatrix}u_1 & u_2 & u_3\\v_1 & v_2 & v_3\\w_1 & w_2 & w_3\end{vmatrix} \nonumber \]
na
\[\vecs u⋅(\vecs w×\vecs v)=\begin{vmatrix}u_1 & u_2 & u_3\\w_1 & w_2 & w_3\\v_1 & v_2 & v_3\end{vmatrix}. \nonumber \]
Tunaweza kupata determinant kwa ajili ya kuhesabu\(\vecs u⋅(\vecs w×\vecs v)\) kwa kubadili chini safu mbili za\(\vecs u⋅(\vecs v×\vecs w).\) Kwa hiyo,\(\vecs u⋅(\vecs v×\vecs w)=−\vecs u⋅(\vecs w×\vecs v).\)
Kufuatia hoja hii na kuchunguza njia tofauti tunaweza kubadilishana vigezo katika bidhaa mara tatu scalar kusababisha utambulisho zifuatazo:
\ [kuanza {align}\ vecs u(\ vecs v×\ vecs w) & =\ vecs (\ vecs w×\ vecs v)\\ [10pt]
\ vecs u(\ vecs v×\ vecs w) &=\ vecs u (\ vecs u ×\ vecs u) =\ vecs u× (\ vecs u ×\ vecs v). \ mwisho {align}\ nonumber\]
Hebu\(\vecs u\) na\(\vecs v\) uwe vectors mbili katika nafasi ya kawaida. Ikiwa\(\vecs u\) na\(\vecs v\) sio mchanganyiko wa kila mmoja, basi vectors hizi huunda pande zilizo karibu za parallelogram. Tuliona katika Kumbuka kwamba eneo la parallelogram hii ni\(‖\vecs u×\vecs v‖\). Sasa tuseme tunaongeza vector ya tatu\(\vecs w\) ambayo haina uongo katika ndege sawa\(\vecs u\) na\(\vecs v\) lakini bado inashiriki hatua sawa ya awali. Kisha wadudu hawa huunda pembe tatu za parallelepiped, mche wa tatu-dimensional na nyuso sita ambazo ni kila parallelograms, kama inavyoonekana katika Kielelezo\(\PageIndex{7}\). Kiasi cha prism hii ni bidhaa ya urefu wa takwimu na eneo la msingi wake. Bidhaa tatu ya scalar ya\(\vecs u,\vecs v,\) na\(\vecs w\) hutoa njia rahisi ya kuhesabu kiasi cha parallelepiped iliyoelezwa na wadudu hawa.
Kiasi cha parallelepiped na mipaka ya karibu iliyotolewa na vectors\(\vecs u,\vecs v\), na\(\vecs w\) ni thamani kamili ya bidhaa tatu za scalar (Kielelezo\(\PageIndex{7}\)):
\[V=||\vecs u⋅(\vecs v×\vecs w)||. \nonumber \]
Kumbuka kwamba, kama jina linavyoonyesha, bidhaa tatu za scalar hutoa scalar. Fomu ya kiasi iliyotolewa tu inatumia thamani kamili ya kiasi cha scalar.
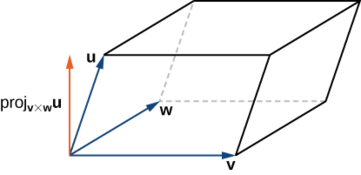
Eneo la msingi wa parallelepiped hutolewa na Urefu\(‖\vecs v×\vecs w‖.\) wa takwimu hutolewa na Kiasi\(\|\text{proj}_{\vecs v×\vecs w}\vecs u\|.\) cha parallelepiped ni bidhaa ya urefu na eneo la msingi, kwa hiyo tuna
\ [kuanza {align*} V &=\ maandishi {proj} _ {\ vecs v×\ vecs w}\ vecs u\ vecs v×\ vecs\\ vecs\\ vecs w\\ vecs\\ vecs w)} {\ vecs vecs v×\ vecs waccus}\ vecs v×\ vecs with\\ [4pt]
&=\ |\ vecs u(\ vecs v×\ vecs w)\ |.
\ mwisho {align*}\]
□
Hebu\(\vecs u=⟨−1,−2,1⟩,\vecs v=⟨4,3,2⟩,\) na\(\vecs w=⟨0,−5,−2⟩\). Pata kiasi cha parallelepiped na kando karibu\(\vecs u,\vecs v\), na\(\vecs w\) (Kielelezo\(\PageIndex{8}\)).
Suluhisho
Tuna
\ [kuanza {align*}\ vecs u(\ vecs v×\ vecs w) &=\ kuanza {vmatrix} -1 & Δ 2 & 1\\ 4 & 2 & 0 & -5 & -2\ mwisho {vmatrix}\\ [4pt]
&= (-1)\ kuanza {vmatrix} 3 & 2 & -1\\ mwisho {vmatrix} +2\ kuanza {vmatrix} 4 & 2\ 0 & -1\ mwisho {vmatrix} +\ kuanza {vmatrix} 4 & 3\\ 0 & -5\ mwisho { vmatrix}\\ [4pt]
& = (-1) (-6+10) +2 (-8—0) + (-20—0)\\ [4pt]
&=-4,116-20\\ [4pt]
&=-40. \ mwisho {align*}\]
Hivyo, kiasi cha parallelepiped ni\(|−40|=40\) vitengo 3
Pata kiasi cha parallelepiped kilichoundwa na vectors\(\vecs a=3\mathbf{\hat i}+4\mathbf{\hat j}−\mathbf{\hat k}, \vecs b=2\mathbf{\hat i}−\mathbf{\hat j}−\mathbf{\hat k},\) na\(\vecs c=3\mathbf{\hat j}+\mathbf{\hat k}.\)
- Kidokezo
-
Tumia bidhaa tatu za scalar kwa kutafuta uamuzi.
- Jibu
-
\(8\)vitengo 3
Matumizi ya Bidhaa ya Msalaba
Bidhaa ya msalaba inaonekana katika maombi mengi ya vitendo katika hisabati, fizikia, na uhandisi. Hebu tuchunguze baadhi ya programu hizi hapa, ikiwa ni pamoja na wazo la wakati, ambalo tulianza sehemu hii. Maombi mengine yanaonekana katika sura za baadaye, hasa katika utafiti wetu wa mashamba ya vector kama vile mashamba ya mvuto na umeme (Utangulizi wa Vector Calculus).
Kutumia bidhaa mara tatu scalar kuonyesha kwamba wadudu\(\vecs u=⟨2,0,5⟩,\vecs v=⟨2,2,4⟩\), na\(\vecs w=⟨1,−1,3⟩\) ni coplanar-yaani, kuonyesha kwamba wadudu hawa uongo katika ndege moja.
Suluhisho
Anza kwa kuhesabu bidhaa tatu za scalar ili kupata kiasi cha parallelepiped iliyoelezwa\(\vecs u,\vecs v,\) na\(\vecs w\):
\ [kuanza {align*}\ vecs u(\ vecs v×\ vecs w) &=\ kuanza {vmatrix} 2 & 0 & 5\ 2 & 4\ 1 & -1 & -1 & 3\ mwisho {Matrix}\\ [4pt]
&= [2) (3) + (0) (4) (1) +5 (2) (-1)] [5 (2) (1) + (2) (4) (-1) + (0) (2) (3)]\\ [4pt]
&=2,12 =0. \ mwisho {align*}\]
Kiasi cha parallelepiped ni\(0\) vitengo 3, hivyo moja ya vipimo lazima iwe sifuri. Kwa hiyo, wadudu watatu wote hulala katika ndege moja.
Je, vectors\(\vecs a=\mathbf{\hat i}+\mathbf{\hat j}−\mathbf{\hat k}, \vecs b=\mathbf{\hat i}−\mathbf{\hat j}+\mathbf{\hat k},\) na\(\vecs c=\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k}\) coplanar?
- Kidokezo
-
Tumia bidhaa tatu za scalar.
- Jibu
-
Hapana, bidhaa tatu za scalar ni\(−4≠0,\) hivyo vectors tatu huunda kando ya karibu ya parallelepiped. Wao si coplanar.
Ndege moja tu inaweza kupita kwenye seti yoyote ya pointi tatu zisizo za kawaida. Find orthogonal vector kwa ndege zenye pointi\(P=(9,−3,−2),Q=(1,3,0),\) na\(R=(−2,5,0).\)
Suluhisho
Ndege lazima iwe na vectors\(\vecd{PQ}\) na\(\vecd{QR}\):
\(\vecd{PQ}=⟨1−9,3−(−3),0−(−2)⟩=⟨−8,6,2⟩\)
\(\vecd{QR}=⟨−2−1,5−3,0−0⟩=⟨−3,2,0⟩.\)
Bidhaa ya msalaba\(\vecd{PQ}×\vecd{QR}\) inazalisha vector orthogonal kwa wote\(\vecd{PQ}\) na\(\vecd{QR}\). Kwa hiyo, bidhaa ya msalaba ni orthogonal kwa ndege ambayo ina vectors hizi mbili:
\ [kuanza {align*}\ vecd {PQ} ×\ vecd {QR} &=\ kuanza {vmatrix}\ hisabati {\ kofia i} &\ mathbf {\ kofia j} &\ hesabu {\ kofia k}\\ 18-8 & 6 & 2\ -3 & 2 & 0\ mwisho {vmatrix}\\ [4pt]
&= 0\ mathbf {\ kofia i} -6\ mathbf {\ kofia j} -16\ mathbf {\ kofia k} - (-18\ mathbf {\ kofia k} +4\ hatbf {\ kofia i} +0\ hatbf {\ kofia j})\\ [4pt]
&=—4\ mathbf {\ hat i} -6\ mathbf {\ kofia j} +2\ mathbf {\ kofia k}. \ mwisho {align*}\]
Tumeona jinsi ya kutumia bidhaa tatu za scalar na jinsi ya kupata vector orthogonal kwa ndege. Sasa tunatumia bidhaa ya msalaba kwa hali halisi ya ulimwengu.
Wakati mwingine nguvu husababisha kitu kugeuka. Kwa mfano, kugeuka screwdriver au wrench inajenga aina hii ya athari ya mzunguko, inayoitwa moment.
Torque,\(\vecs \tau\) (barua ya Kigiriki tau), inachukua tabia ya nguvu ya kuzalisha mzunguko kuhusu mhimili wa mzunguko. Hebu\(\vecs r\) kuwa vector na hatua ya awali iko kwenye mhimili wa mzunguko na kwa hatua ya mwisho iko mahali ambapo nguvu inatumiwa, na basi vector\(\vecs F\) inawakilisha nguvu. Kisha moment ni sawa na bidhaa msalaba wa\(r\) na\(F\):
\[\vecs \tau=\vecs r×\vecs F. \nonumber \]
Angalia Kielelezo\(\PageIndex{9}\).
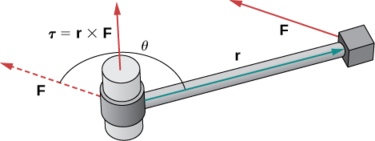
Fikiria juu ya kutumia wrench ili kuimarisha bolt. Wakati huo τ kutumika kwa bolt inategemea jinsi ngumu sisi kushinikiza wrench (nguvu) na jinsi mbali juu ya kushughulikia sisi kutumia nguvu (umbali). Wakati huongezeka kwa nguvu kubwa juu ya wrench kwa umbali mkubwa kutoka kwenye bolt. Vitengo vya kawaida vya wakati ni mita ya newton au pound-pound. Ingawa moment ni dimensionally sawa na kazi (ina vitengo sawa), dhana mbili ni tofauti. Torque hutumiwa hasa katika mazingira ya mzunguko, wakati kazi kawaida inahusisha mwendo kando ya mstari.
Bolt imeimarishwa kwa kutumia nguvu ya\(6\) N kwa wrench 0.15-m (Kielelezo\(\PageIndex{10}\)). Pembe kati ya wrench na vector nguvu ni\(40°\). Pata ukubwa wa wakati kuhusu katikati ya bolt. Pindua jibu kwa maeneo mawili ya decimal.
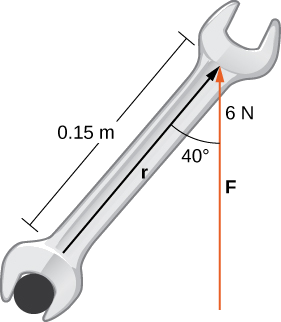
Suluhisho:
Badilisha taarifa iliyotolewa katika equation kufafanua moment:
\ [kuanza {align*}}}\ vecs τ& =\ |\ vecs r\\ vecs F\ |\\ [4pt]
&=\ vecs r\ vecs F\ sin\ [4pt]
& =( 0.15\,\ maandishi {m}) (6\\ maandishi {N})\ dhambi 40°\\ [4pt]
&≈ 0.8] 58\,\ maandishi {nm.} \ mwisho {align*}\]
Tumia nguvu inayotakiwa kuzalisha\(15\) nm moment kwa pembe ya\(30º\) kutoka fimbo\(150\) -cm.
- Kidokezo
-
\(‖\vecs τ‖=15\)nm na\(‖\vecs r‖=1.5\) m
- Jibu
-
\(20\)N
Dhana muhimu
- Bidhaa ya msalaba\(\vecs u×\vecs v\) wa vectors mbili\(\vecs u=⟨u_1,u_2,u_3⟩\) na\(\vecs v=⟨v_1,v_2,v_3⟩\) ni vector orthogonal kwa wote\(\vecs u\) na\(\vecs v\). Urefu wake hutolewa na\(‖\vecs u×\vecs v‖=‖\vecs u‖⋅‖\vecs v‖⋅\sin θ,\) wapi\(θ\) pembe kati\(\vecs u\) na\(\vecs v\). Mwelekeo wake hutolewa na utawala wa mkono wa kulia.
- Fomu ya algebraic kwa kuhesabu bidhaa za msalaba wa vectors mbili,
\(\vecs u=⟨u_1,u_2,u_3⟩\)na\(\vecs v=⟨v_1,v_2,v_3⟩\), ni
\(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k}.\)
- Bidhaa ya msalaba inatimiza mali zifuatazo kwa vectors\(\vecs u,\vecs v,\) na\(\vecs w\), na scalar\(c\):
\(\vecs u×\vecs v=−(\vecs v×\vecs u)\)
\(\vecs u×(\vecs v+\vecs w)=\vecs u×\vecs v+\vecs u×\vecs w\)
\(c(\vecs u×\vecs v)=(c\vecs u)×\vecs v=\vecs u×(c\vecs v)\)
\(\vecs u×\vecs 0=\vecs 0×\vecs u=\vecs 0\)
\(\vecs v×\vecs v=\vecs 0\)
\(\vecs u⋅(\vecs v×\vecs w)=(\vecs u×\vecs v)⋅\vecs w\)
- Bidhaa ya msalaba wa vectors\(\vecs u=⟨u_1,u_2,u_3⟩\) na\(\vecs v=⟨v_1,v_2,v_3⟩\) ni kuamua\(\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\u_1 & u_2 & u_3\\v_1 & v_2 & v_3\end{vmatrix}\)
- Ikiwa vectors\(\vecs u\) na\(\vecs v\) kuunda pande karibu za parallelogram, basi eneo la parallelogram linatolewa na\(\|\vecs u×\vecs v\|.\)
- Bidhaa tatu za scalar ya vectors\(\vecs u, \vecs v,\) na\(\vecs w\) ni\(\vecs u⋅(\vecs v×\vecs w).\)
- kiasi cha parallelepiped na edges karibu iliyotolewa na wadudu\(\vecs u,\vecs v\), na\(\vecs w\) ni\(V=|\vecs u⋅(\vecs v×\vecs w)|.\)
- Ikiwa bidhaa tatu za scalar za vectors\(\vecs u,\vecs v,\) na\(\vecs w\) ni sifuri, basi vectors ni coplanar. Kuzungumza pia ni kweli: Ikiwa vectors ni coplanar, basi bidhaa zao tatu za scalar ni sifuri.
- Bidhaa ya msalaba inaweza kutumika kutambua vector orthogonal kwa vectors mbili zilizopewa au ndege.
- Torque\(\vecs τ\) hatua tabia ya nguvu ya kuzalisha mzunguko kuhusu mhimili wa mzunguko. Ikiwa nguvu\(\vecs F\) inafanya kazi kwa mbali (uhamisho)\(\vecs r\) kutoka kwa mhimili, basi wakati huo ni sawa na bidhaa ya msalaba\(\vecs r\) na\(\vecs F: \vecs τ=\vecs r×\vecs F.\)
Mlinganyo muhimu
- Bidhaa ya msalaba wa vectors mbili kwa suala la vectors kitengo
\[\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k} \nonumber \]
faharasa
bidhaa msalaba
\(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k},\)wapi\(\vecs u=⟨u_1,u_2,u_3⟩\) na\(\vecs v=⟨v_1,v_2,v_3⟩\)
kiamuzi
nambari halisi inayohusishwa na tumbo la mraba
parallelepiped
prism tatu-dimensional na nyuso sita ambazo ni parallelograms
moment
athari za nguvu ambayo inasababisha kitu kugeuka
bidhaa tatu za scalar
bidhaa ya dot ya vector na bidhaa ya msalaba wa vectors nyingine mbili:\(\vecs u⋅(\vecs v×\vecs w)\)
bidhaa ya vector
bidhaa ya msalaba wa vectors mbili


