12.3: Bidhaa ya Dot

Malengo ya kujifunza

• Tumia bidhaa ya dot ya vectors mbili zilizopewa.
• Kuamua kama vectors mbili zilizopewa ni perpendicular.
• Kupata cosines mwelekeo wa vector kupewa.
• Eleza nini maana ya makadirio ya vector ya vector moja kwenye vector nyingine, na kuelezea jinsi ya kuihesabu.
• Tumia kazi iliyofanywa na nguvu iliyotolewa.

Ikiwa tunatumia nguvu kwa kitu ili kitu kitakwenda, tunasema kwamba kazi imefanywa na nguvu. Hapo awali, tuliangalia nguvu ya mara kwa mara na tulidhani nguvu ilitumika katika mwelekeo wa mwendo wa kitu. Chini ya hali hizo, kazi inaweza kuelezwa kama bidhaa ya nguvu inayofanya kitu na umbali kitu kinachoendelea. Katika sura hii, hata hivyo, tumeona kwamba wote nguvu na mwendo wa kitu inaweza kuwakilishwa na wadudu.

Katika sehemu hii, tunaendeleza operesheni inayoitwa bidhaa ya dot, ambayo inaruhusu sisi kuhesabu kazi katika kesi wakati vector nguvu na vector mwendo wana mwelekeo tofauti. Bidhaa ya dot kimsingi inatuambia kiasi gani cha vector nguvu kinatumika katika mwelekeo wa vector mwendo. Bidhaa ya dot pia inaweza kutusaidia kupima angle iliyoundwa na jozi ya vectors na nafasi ya vector jamaa na axes kuratibu. Hata hutoa mtihani rahisi kuamua kama vectors mbili hukutana kwa pembe ya kulia.

Bidhaa ya Dot na Mali Zake

Tayari tumejifunza jinsi ya kuongeza na kuondoa vectors. Katika sura hii, sisi kuchunguza aina mbili za kuzidisha vector. Aina ya kwanza ya kuzidisha vector inaitwa bidhaa ya dot, kulingana na notation tunayotumia kwa ajili yake, na inaelezwa kama ifuatavyo:

Ufafanuzi: dot bidhaa

Bidhaa ya dot ya vectors\(\vecs{ u}=⟨u_1,u_2,u_3⟩\) na\(\vecs{ v}=⟨v_1,v_2,v_3⟩\) hutolewa kwa jumla ya bidhaa za vipengele

\[\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3. \nonumber \]

Kumbuka kwamba ikiwa\(u\) na\(v\) ni vectors mbili-dimensional, tunahesabu bidhaa ya dot kwa mtindo sawa. Hivyo, kama\(\vecs{ u}=⟨u_1,u_2⟩\) na\(\vecs{ v}=⟨v_1,v_2⟩,\) kisha

\[\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2. \nonumber \]

Wakati vectors mbili zimeunganishwa chini ya kuongeza au kuondoa, matokeo ni vector. Wakati vectors mbili zinajumuishwa kwa kutumia bidhaa ya dot, matokeo ni scalar. Kwa sababu hii, bidhaa ya dot mara nyingi huitwa bidhaa ya scalar. Inaweza pia kuitwa bidhaa za ndani.

Mfano\(\PageIndex{1}\): Calculating Dot Products

1. Kupata dot bidhaa ya\(\vecs{ u}=⟨3,5,2⟩\) na\(\vecs{ v}=⟨−1,3,0⟩\).
2. Kupata bidhaa scalar ya\(\vecs{ p}=10\hat{\textbf i}−4 \hat{\textbf j}+7 \hat{\textbf k}\) na\(\vecs{ q}=−2\hat{\textbf i}+\hat{\textbf j}+6\hat{\textbf k}.\)

Suluhisho:

a Badilisha vipengele vector katika formula kwa bidhaa dot:

\[ \begin{align*} \vecs{ u}⋅\vecs{ v} &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &=3(−1)+5(3)+2(0) \\[4pt] &=−3+15+0 \\[4pt] &=12. \end{align*}\]

b. hesabu ni sawa kama vectors imeandikwa kwa kutumia kiwango kitengo vectors. Bado tuna vipengele vitatu kwa vector kila mbadala katika formula kwa bidhaa dot:

\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=p_1q_1+p_2q_2+p_3q_3 \\[4pt] &=10(−2)+(−4)(1)+(7)(6) \\[4pt] &=−20−4+42 \\[4pt] &=18.\end{align*}\]

Zoezi\(\PageIndex{1}\)

Kupata\(\vecs{ u}⋅\vecs{ v}\), wapi\(\vecs{ u}=⟨2,9,−1⟩\) na\(\vecs{ v}=⟨−3,1,−4⟩.\)

Kidokezo

Panua vipengele vinavyolingana na kisha uongeze bidhaa zao.

Jibu

\(7\)

Kama kuongeza vector na kuondoa, bidhaa dot ina mali kadhaa algebraic. Sisi kuthibitisha tatu ya mali hizi na kuondoka wengine kama mazoezi.

Mali ya Bidhaa ya Dot

Hebu\(\vecs{ u}\)\(\vecs{ v}\), na\(\vecs{ w}\) uwe wadudu, na\(c\) uwe na scalar.

1. Mali ya kubadilisha\[\vecs{ u}⋅\vecs{ v}=\vecs{ v}⋅\vecs{ u} \nonumber \]
2. Mali ya kusambaza\[\vecs{ u}⋅(\vecs{ v}+\vecs{ w})=\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ w} \nonumber \]
3. Mali ya ushirika\[c(\vecs{ u}⋅\vecs{ v})=(c\vecs{ u})⋅\vecs{ v}=\vecs{ u}⋅(c\vecs{ v}) \nonumber \]
4. Mali ya ukubwa\[\vecs{ v}⋅\vecs{ v}=\|\vecs{ v}\|^2 \nonumber \]

Ushahidi

Hebu\(\vecs{ u}=⟨u_1,u_2,u_3⟩\) na\(\vecs{ v}=⟨v_1,v_2,v_3⟩.\) kisha

\[ \begin{align*} \vecs{ u}⋅\vecs{ v} &=⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &= v_1u_1+v_2u_2+v_3u_3 \\[4pt] &= ⟨v_1,v_2,v_3⟩⋅⟨u_1,u_2,u_3⟩ \\[4pt] &=\vecs{ v}⋅\vecs{ u}.\end{align*}\]

Mali ya ushirika inaonekana kama mali ya ushirika kwa kuzidisha idadi halisi, lakini makini sana na tofauti kati ya vitu vya scalar na vector:

\[ \begin{align*} c(\vecs{ u}⋅\vecs{ v}) &=c(u_1v_1+u_2v_2+u_3v_3) \\[4pt] &=c(u_1v_1)+c(u_2v_2)+c(u_3v_3) \\[4pt] &=(cu_1)v_1+(cu_2)v_2+(cu_3)v_3 \\[4pt] &=⟨cu_1,cu_2,cu_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=c⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=(c\vecs{ u})⋅\vecs{ v}.\end{align*}\]

Ushahidi kwamba\(c(\vecs{ u}⋅\vecs{ v})=\vecs{ u}⋅(c\vecs{ v})\) ni sawa.

Mali ya nne inaonyesha uhusiano kati ya ukubwa wa vector na bidhaa yake ya dot yenyewe:

\[ \begin{align*} \vecs{ v}⋅\vecs{ v} &=⟨v_1,v_2,v_3⟩⋅⟨v_1,v_2,v_3⟩\\[4pt] &=(v_1)^2+(v_2)^2+(v_3)^2 \\[4pt] &=\left[\sqrt{(v_1)^2+(v_2)^2+(v_3)^2}\right]^2 \\[4pt] &=\|\vecs{ v}\|^2.\end{align*}\]

□

Kumbuka kuwa ufafanuzi wa bidhaa dot mavuno\(\vecs{ 0}⋅\vecs{ v}=0.\) By mali iv. kama\(\vecs{ v}⋅\vecs{ v}=0,\) basi\(\vecs{ v}=\vecs{ 0}.\)

Mfano\(\PageIndex{2}\): Using Properties of the Dot Product

Hebu\(\vecs{ a}=⟨1,2,−3⟩\),\(\vecs{ b}=⟨0,2,4⟩\), na\( \vecs{ c} =⟨5,−1,3⟩\).

Kupata kila moja ya bidhaa zifuatazo.

1. \(( \vecs{ a} ⋅ \vecs{ b}) \vecs{ c} \)
2. \(\vecs{ a}⋅(2\vecs{ c})\)
3. \(\|\vecs{ b}\|^2\)

Suluhisho

a. Kumbuka kwamba maneno haya anauliza kwa scalar nyingi ya\(\vecs{ c}\) na\(\vecs{ a}⋅\vecs{ b}\):

\[ \begin{align*} (\vecs{ a}⋅\vecs{ b})\vecs{ c} &=(⟨1,2,−3⟩⋅⟨0,2,4⟩)⟨5,−1,3⟩ \\[4pt] &=(1(0)+2(2)+(−3)(4))⟨5,−1,3⟩ \\[4pt] &=−8⟨5,−1,3⟩ \\[4pt] &= ⟨−40,8,−24⟩.\end{align*}\]

b. usemi huu ni dot bidhaa ya vector\(\vecs{ a}\) na scalar nyingi 2\(\vecs{ c}\):

\[ \begin{align*} \vecs{ a}⋅(2\vecs{ c}) &=2(\vecs{ a}⋅\vecs{ c}) \\[4pt] &=2(⟨1,2,−3⟩⋅⟨5,−1,3⟩) \\[4pt] &=2(1(5)+2(−1)+(−3)(3)) \\[4pt] &=2(−6)=−12.\end{align*}\]

c Kurahisisha maneno haya ni matumizi ya moja kwa moja ya bidhaa ya dot:

\[ \begin{align*} \|\vecs{ b}\|^2 &=\vecs{ b}⋅\vecs{ b} \\[4pt] &=⟨0,2,4⟩⋅⟨0,2,4⟩\\[4pt] &=0^2+2^2+4^2\\[4pt] &=0+4+16\\[4pt] &=20.\end{align*}\]

Zoezi\(\PageIndex{2}\)

Kupata bidhaa zifuatazo kwa\(\vecs{ p}=⟨7,0,2⟩\),\(\vecs{ q}=⟨−2,2,−2⟩\), na\(\vecs{ r}=⟨0,2,−3⟩\).

1. \((\vecs{ r}⋅\vecs{ p})\vecs{ q}\)
2. \(\|\vecs{ p}\|^2\)

Kidokezo

\(\vecs{ r}⋅\vecs{ p}\)ni scalar.

Jibu

\(a. \quad (\vecs{ r}⋅\vecs{ p})\vecs{ q}=⟨12,−12,12⟩; \quad b. \quad \|\vecs{ p}\|^2=53\)

Kutumia Bidhaa ya Dot ili Kupata Angle kati ya Vectors mbili

Wakati vectors mbili zisizo na zero zinawekwa katika nafasi ya kawaida, iwe katika vipimo viwili au vipimo vitatu, huunda angle kati yao (Kielelezo\(\PageIndex{1}\)). Bidhaa ya dot hutoa njia ya kupata kipimo cha angle hii. Mali hii ni matokeo ya ukweli kwamba tunaweza kuelezea bidhaa ya dot kwa suala la cosine ya angle iliyoundwa na vectors mbili.

Kielelezo\(\PageIndex{1}\): Hebu\(θ\) kuwa angle kati ya vectors mbili nonzero\(\vecs{ u}\) na\(\vecs{ v}\) vile kwamba \(0≤θ≤π\).

Kutathmini Bidhaa ya Dot

Bidhaa ya dot ya vectors mbili ni bidhaa ya ukubwa wa kila vector na cosine ya angle kati yao:

\[\vecs{ u}⋅\vecs{ v}=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{evaldot} \]

Ushahidi

Weka vectors\(\vecs{ u}\) na\(\vecs{ v}\) katika nafasi ya kawaida na fikiria vector\(\vecs{ v}−\vecs{ u}\) (Kielelezo\(\PageIndex{2}\)). Vectors hizi tatu huunda pembetatu na urefu wa upande\(‖\vecs{ u}‖,‖\vecs{ v}‖\), na\(‖\vecs{ v}−\vecs{ u}‖\).

Kielelezo\(\PageIndex{2}\): Urefu wa pande za pembetatu hutolewa na ukubwa wa vectors zinazounda pembetatu.

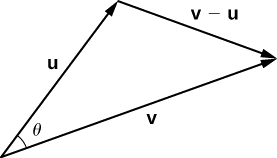
Kumbuka kutoka kwa trigonometry kwamba sheria ya cosines inaelezea uhusiano kati ya urefu wa upande wa pembetatu na angle\(θ\). Kutumia sheria ya cosines hapa inatoa

\[‖\vecs{ v}−\vecs{ u}‖^2=‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{eq20} \]

Bidhaa ya dot hutoa njia ya kuandika upya upande wa kushoto wa Equation\ ref {eq20}:

\[ \begin{align*} ‖\vecs{ v}−\vecs{ u}‖^2 &=(\vecs{ v}−\vecs{ u})⋅(\vecs{ v}−\vecs{ u}) \\[4pt] &=(\vecs{ v}−\vecs{ u})⋅\vecs{ v}−(\vecs{ v}−\vecs{ u})⋅\vecs{ u} \\[4pt] &=\vecs{ v}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}−\vecs{ v}⋅\vecs{ u}+\vecs{ u}⋅\vecs{ u} \\[4pt] &=\vecs{ v}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ u} \\[4pt] &=‖\vecs{ v}‖^2−2\vecs{ u}⋅\vecs{ v}+‖\vecs{ u}‖^2.\end{align*}\]

Kuingiza katika sheria ya mavuno ya cosines

\[ \begin{align*} ‖\vecs{ v}−\vecs{ u}‖^2 &=‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] ‖\vecs{ v}‖^2−2\vecs{ u}⋅\vecs{ v}+‖\vecs{ u}‖^2 &= ‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] −2\vecs{ u}⋅\vecs{ v} &=−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] \vecs{ u}⋅\vecs{ v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \end{align*}\]

□

Tunaweza kutumia fomu ya bidhaa ya dot katika Equation\ ref {evaldot} ili kupata kipimo cha angle kati ya wadudu wawili wasio na sifuri kwa kupanga upya Equation\ ref {evaldot} ili kutatua kwa cosine ya angle:

\[\cos θ=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}. \label{dot2} \]

Kutumia equation hii, tunaweza kupata cosine ya angle kati ya vectors mbili nonzero. Kwa kuwa tunazingatia angle ndogo kati ya vectors, tunadhani\(0°≤θ≤180°\) (au\(0≤θ≤π\) ikiwa tunafanya kazi kwa radians). Cosine inverse ni ya kipekee juu ya aina hii, kwa hiyo tunaweza kuamua kipimo cha angle\(θ\).

Mfano\(\PageIndex{3}\): Finding the Angle between Two Vectors

Pata kipimo cha angle kati ya kila jozi ya vectors.

1. \(\mathbf{\hat i} + \mathbf{\hat j} + \mathbf{\hat k}\)na\(2\mathbf{\hat i} – \mathbf{\hat j} – 3\mathbf{\hat k}\)
2. \(⟨2,5,6⟩\)na\(⟨−2,−4,4⟩\)

Suluhisho

a Ili kupata cosine ya angle iliyoundwa na wadudu wawili, badala ya vipengele vya wadudu katika Equation\ ref {dot2}:

\[ \begin{align*} \cos θ &=\dfrac{(\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k})⋅(2\mathbf{\hat i}−\mathbf{\hat j}−3\mathbf{\hat k})}{∥\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k}∥⋅∥2\mathbf{\hat i}−\mathbf{\hat j}−3\mathbf{\hat k}∥} \\[4pt] &=\dfrac{1(2)+(1)(−1)+(1)(−3)}{\sqrt{1^2+1^2+1^2}\sqrt{2^2+(−1)^2+(−3)^2}} \\[4pt] &=\dfrac{−2}{\sqrt{3}\sqrt{14}} =\dfrac{−2}{\sqrt{42}}. \end{align*}\]

Kwa hiyo,\(θ=\arccos\dfrac{−2}{\sqrt{42}}\) rad.

b Anza kwa kutafuta thamani ya cosine ya angle kati ya vectors:

\[ \begin{align*} \cos θ &=\dfrac{⟨2,5,6⟩⋅⟨−2,−4,4⟩}{∥⟨2,5,6⟩∥⋅∥⟨−2,−4,4⟩∥} \\[4pt] &=\dfrac{2(−2)+(5)(−4)+(6)(4)}{\sqrt{2^2+5^2+6^2}\sqrt{(−2)^2+(−4)^2+4^2}} \\[4pt] &=\dfrac{0}{\sqrt{65}\sqrt{36}}=0.\end{align*}\]

Sasa,\(\cos θ=0\) na\(0≤θ≤π\), hivyo\(θ=π/2\).

Zoezi\(\PageIndex{3}\)

Pata kipimo cha angle, katika radians, iliyoundwa na vectors\(\vecs{ a}=⟨1,2,0⟩\) na\(\vecs{ b}=⟨2,4,1⟩\). Pande zote hadi karibu na mia moja.

Kidokezo

Tumia Equation\ ref {dot2}.

Jibu

\(θ≈0.22\)rad

Pembe kati ya vectors mbili inaweza kuwa\((0<\cos θ<1),\) obtuse papo hapo\((−1<\cos θ<0)\), au moja kwa moja\((\cos θ=−1)\). Ikiwa\(\cos θ=1\), basi vectors wote wana mwelekeo sawa. Ikiwa\(\cos θ=0\), basi vectors, wakati kuwekwa katika nafasi ya kawaida, fanya angle sahihi (Kielelezo\(\PageIndex{3}\)). Tunaweza kurasimisha matokeo haya katika theorem kuhusu vectors orthogonal (perpendicular).

Kielelezo\(\PageIndex{3}\): (a) Angle ya papo hapo ina\(0<\cos θ<1\). (b) angle obtuse ina\(−1<\cos θ<0.\) (c) line moja kwa moja ina\(\cos θ=−1\). (d) Kama wadudu wana mwelekeo huo,\(\cos θ=1\). (e) Kama wadudu ni orthogonal (perpendicular),\(\cos θ=0.\)

Orthogonal wadudu

Vectors nonzero\(\vecs{u}\) na\(\vecs{v}\) ni vectors orthogonal kama na tu kama\(\vecs{u}⋅\vecs{v}=0.\)

Ushahidi

Hebu\(\vecs{u}\) na\(\vecs{v}\) kuwa vectors nonzero, na hebu\(θ\) kuashiria angle kati yao. Kwanza, kudhani\(\vecs{u}⋅\vecs{v}=0.\) Kisha

\[‖\vecs{u}‖‖\vecs{v}‖\cos θ=0. \nonumber \]

Hata hivyo,\(‖\vecs{u}‖≠0\) na\(‖\vecs{v}‖≠0,\) hivyo ni lazima tuwe na\(\cos θ=0\). Kwa hiyo\(θ=90°\), na vectors ni orthogonal.

Sasa kudhani\(\vecs{u}\) na\(\vecs{v}\) ni orthogonal. Kisha\(θ=90°\) na tuna

\[ \begin{align*} \vecs{u}⋅\vecs{v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖\cos 90° \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖(0) \\[4pt] &=0. \end{align*}\]

□

Maneno ya orthogonal, perpendicular, na ya kawaida kila yanaonyesha kwamba vitu vya hisabati vinaingiliana kwenye pembe za kulia. Matumizi ya kila neno imedhamiriwa hasa na muktadha wake. Tunasema kwamba vectors ni orthogonal na mistari ni perpendicular. Neno la kawaida hutumiwa mara nyingi wakati wa kupima angle iliyofanywa na ndege au uso mwingine.

Mfano\(\PageIndex{4}\): Identifying Orthogonal Vectors

Kuamua kama\(\vecs{p}=⟨1,0,5⟩\) na\(\vecs{q}=⟨10,3,−2⟩\) ni vectors orthogonal.

Suluhisho

Kutumia ufafanuzi, tunahitaji tu kuangalia bidhaa ya dot ya vectors:

\[ \vecs{ p}⋅\vecs{ q}=1(10)+(0)(3)+(5)(−2)=10+0−10=0. \nonumber \]

Kwa sababu\(\vecs{p}⋅\vecs{q}=0,\) vectors ni orthogonal (Kielelezo\(\PageIndex{4}\)).

Kielelezo\(\PageIndex{4}\): Vectors\(\vecs{ p}\) na\(\vecs{ q}\) kuunda angle sahihi wakati pointi zao za awali zimeunganishwa.

Zoezi\(\PageIndex{4}\)

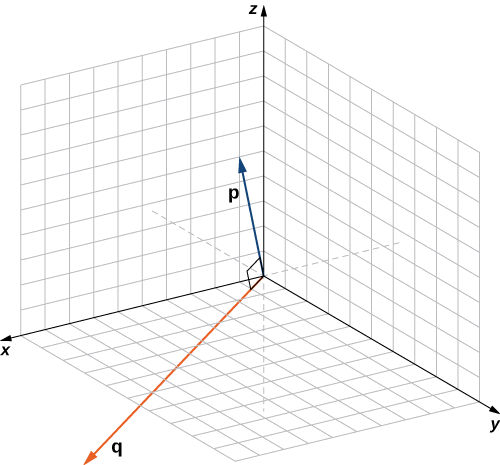
Kwa thamani gani ya\(x\) ni\(\vecs{ p}=⟨2,8,−1⟩\) orthogonal kwa\(\vecs{ q}=⟨x,−1,2⟩\)?

Kidokezo

Vectors\(\vecs{ p}\) na\(\vecs{ q}\) ni orthogonal kama na tu kama\(\vecs{ p}⋅\vecs{ q}=0\).

Jibu

\(x=5\)

Mfano\(\PageIndex{5}\): Measuring the Angle Formed by Two Vectors

Hebu\(\vecs{ v}=⟨2,3,3⟩.\) Tafuta hatua za pembe zilizoundwa na wadudu wafuatayo.

1. \(\vecs{ v}\)na\(\mathbf{\hat i}\)
2. \(\vecs{ v}\)na\(\mathbf{\hat j}\)
3. \(\vecs{ v}\)na\(\mathbf{\hat k}\)

Suluhisho

a.Hebu α kuwa angle iliyoundwa\(\vecs{ v}\) na\(\mathbf{\hat i}\):

\[ \begin{align*} \cos{α} &=\dfrac{\vecs{ v}⋅\mathbf{\hat i}}{‖\vecs{ v}‖⋅\|\mathbf{\hat i}\|}=\dfrac{⟨2,3,3⟩⋅⟨1,0,0⟩}{\sqrt{2^2+3^2+3^2}\sqrt{1}}=\dfrac{2}{\sqrt{22}} \\[4pt] α &=\arccos\dfrac{2}{\sqrt{22}}≈1.130\,\text{rad.} \end{align*}\]

b Hebu β kuwakilisha angle iliyoundwa\(\vecs{ v}\) na\(\mathbf{\hat j}\):

\[ \begin{align*} \cos{β} &=\dfrac{\vecs{ v}⋅\mathbf{\hat j}}{‖\vecs{ v}‖⋅\|\mathbf{\hat j}\|}=\dfrac{⟨2,3,3⟩⋅⟨0,1,0⟩}{\sqrt{2^2+3^2+3^2}\sqrt{1}}=\dfrac{3}{\sqrt{22}} \\[4pt] β &=\arccos\dfrac{3}{\sqrt{22}}≈0.877\,\text{rad.} \end{align*}\]

c Hebu γ kuwakilisha angle iliyoundwa\(\vecs{ v}\) na\(\mathbf{\hat k}\):

\[ \begin{align*} \cos{γ} &=\dfrac{\vecs{ v}⋅\mathbf{\hat k}}{‖\vecs{ v}‖⋅\|\mathbf{\hat k}\|}=\dfrac{⟨2,3,3⟩⋅⟨0,0,1⟩}{\sqrt{2^2+3^2+3^2}\sqrt{1}}=\dfrac{3}{\sqrt{22}} \\[4pt]γ &=\arccos\dfrac{3}{\sqrt{22}}≈0.877\,\text{rad.} \end{align*}\]

Zoezi\(\PageIndex{5}\)

Hebu\(\vecs{ v}=⟨3,−5,1⟩.\) Tafuta kipimo cha pembe zilizoundwa na kila jozi ya vectors.

1. \(\vecs{ v}\)na\(\mathbf{\hat i}\)
2. \(\vecs{ v}\)na\(\mathbf{\hat j}\)
3. \(\vecs{ v}\)na\(\mathbf{\hat k}\)

Kidokezo

\(\mathbf{\hat i}=⟨1,0,0⟩, \mathbf{\hat j}=⟨0,1,0⟩,\)na\(\mathbf{\hat k}=⟨0,0,1⟩\)

Jibu

\(a. α≈1.04\)rad; b.\(β≈2.58\) rad; c.\(γ≈1.40\) rad

Pembe vector hufanya na kila moja ya shoka za kuratibu, inayoitwa angle ya mwelekeo, ni muhimu sana katika hesabu za vitendo, hasa katika uwanja kama vile uhandisi. Kwa mfano, katika uhandisi wa astronautical, angle ambayo roketi inazinduliwa lazima ihakikishwe kwa usahihi. Hitilafu ndogo sana katika pembe inaweza kusababisha roketi kwenda mamia ya maili mbali bila shaka. Pembe za mwelekeo mara nyingi huhesabiwa kwa kutumia bidhaa ya dot na cosines ya pembe, inayoitwa cosines ya mwelekeo. Kwa hiyo, tunafafanua pembe hizi zote na cosines zao.

Ufafanuzi: pembe za mwelekeo

Pembe zilizoundwa na vector isiyo ya zero na axes za kuratibu huitwa pembe za mwelekeo kwa vector (Kielelezo\(\PageIndex{5}\)). Cosines kwa pembe hizi huitwa cosines ya mwelekeo.

Kielelezo\(\PageIndex{5}\): Angle\(α\) huundwa na vector vector\(\vecs{ v}\) na kitengo\(\mathbf{\hat i}\). Angle β huundwa na vector vector\(\vecs{ v}\) na kitengo\(\mathbf{\hat j}\). Angle γ huundwa na vector vector\(\vecs{ v}\) na kitengo\(\mathbf{\hat k}\).

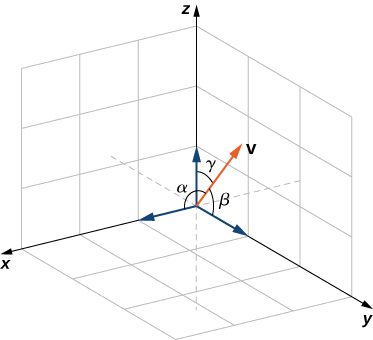
Katika Mfano\(\PageIndex{5}\), mwelekeo\(\vecs{ v}=⟨2,3,3⟩\) cosines ya huduma\(\cos α=\dfrac{2}{\sqrt{22}}, \cos β=\dfrac{3}{\sqrt{22}},\) na\(\cos γ=\dfrac{3}{\sqrt{22}}\). pembe mwelekeo wa\(\vecs{ v}\) ni\(α=1.130\) rad,\(β=0.877\) rad, na\(γ=0.877\) rad.

Hadi sasa, tumezingatia hasa vectors kuhusiana na nguvu, harakati, na nafasi katika nafasi tatu-dimensional kimwili. Hata hivyo, vectors mara nyingi hutumiwa kwa njia zaidi za abstract. Kwa mfano, tuseme muuzaji wa matunda anauza apples, ndizi, na machungwa. Siku fulani, anauza apples 30, ndizi 12, na machungwa 18. Anaweza kutumia vector wingi,\(\vecs{ q}=⟨30,12,18⟩,\) kuwakilisha wingi wa matunda aliyouza siku hiyo. Vile vile, anaweza kutaka kutumia vector bei,\(\vecs{ p}=⟨0.50,0.25,1⟩,\) kuonyesha kwamba yeye anauza apples yake kwa 50¢ kila, ndizi kwa 25¢ kila mmoja, na machungwa kwa $1 kipande. Katika mfano huu, ingawa tunaweza bado grafu wadudu hawa, hatuwezi kutafsiri yao kama uwakilishi halisi wa nafasi katika ulimwengu wa kimwili. Tunatumia vectors tu kuweka wimbo wa vipande fulani vya habari kuhusu apples, ndizi, na machungwa.

Wazo hili linaweza kuonekana kuwa la ajabu, lakini ikiwa tunaangalia tu wadudu kama njia ya kuagiza na kuhifadhi data, tunaona wanaweza kuwa chombo chenye nguvu kabisa. Kurudi kwa muuzaji wa matunda, hebu fikiria kuhusu bidhaa ya dot,\(\vecs{ q}⋅\vecs{ p}\). Tunaihesabu kwa kuzidisha idadi ya apples kuuzwa (30) kwa bei kwa kila apple (50¢), idadi ya ndizi zinazouzwa kwa bei kwa ndizi, na idadi ya machungwa kuuzwa kwa bei kwa kila machungwa. Sisi kisha kuongeza maadili haya yote pamoja. Kwa hiyo, katika mfano huu, bidhaa ya dot inatuambia ni kiasi gani cha fedha ambacho muuzaji wa matunda alikuwa na mauzo siku hiyo.

Tunapotumia vectors kwa njia hii ya jumla, hakuna sababu ya kupunguza idadi ya vipengele hadi tatu. Nini kama muuzaji wa matunda anaamua kuanza kuuza mazabibu? Katika hali hiyo, angependa kutumia vectors nne na bei ya bei ili kuwakilisha idadi ya apples, ndizi, machungwa, na mazabibu ya kuuzwa, na bei zao za kitengo. Kama unaweza kutarajia, kuhesabu bidhaa ya dot ya vectors nne, tunaongeza tu bidhaa za vipengele kama hapo awali, lakini jumla ina maneno manne badala ya tatu.

Mfano\(\PageIndex{6}\): Using Vectors in an Economic Context

AAA Party Supply Store kuuza mialiko, upendeleo chama, mapambo, na vitu huduma ya chakula kama vile sahani karatasi na leso. Wakati AAA hununua hesabu yake, inalipa 25¢ kwa mfuko kwa ajili ya mialiko na neema ya chama. Mapambo yanagharimu AAA 50 kila mmoja, na vitu vya huduma ya chakula vina gharama 20¢ kwa kila mfuko. AAA kuuza mialiko kwa $2.50 kwa mfuko na chama neema kwa $1.50 kwa mfuko. Mapambo huuza $4.50 kila na vitu vya huduma ya chakula kwa $1.25 kwa mfuko.

Wakati wa mwezi wa Mei, AAA Party Supply Store anauza mialiko 1258, 342 neema chama, 2426 mapambo, na 1354 vitu huduma ya chakula. Tumia vectors na bidhaa za dot kuhesabu kiasi gani cha fedha AAA kilichofanywa katika mauzo wakati wa mwezi wa Mei. Duka hilo lilifanya kiasi gani kwa faida?

Suluhisho

Gharama, bei, na vectors wingi ni

\[ \begin{align*} \vecs{ c} &=⟨0.25,0.25,0.50,0.20⟩ \\[4pt] \vecs{ p} &=⟨2.50,1.50,4.50,1.25⟩ \\[4pt] \vecs{ q} &=⟨1258,342,2426,1354⟩. \end{align*}\]

Mauzo ya AAA kwa mwezi wa Mei yanaweza kuhesabiwa kwa kutumia bidhaa ya dot\(\vecs{ p}⋅\vecs{ q}\). Tuna

\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=⟨2.50,1.50,4.50,1.25⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] &=3145+513+10917+1692.5 \\[4pt] &= 16267.5. \end{align*}\]

Hivyo, AAA ilichukua $16,267.50 wakati wa mwezi wa Mei. Ili kuhesabu faida, lazima kwanza tuhesabu kiasi gani AAA kilicholipwa kwa vitu vilivyouzwa. Tunatumia bidhaa ya dot\(\vecs{c}⋅\vecs{q}\) ili kupata

\[ \begin{align*} \vecs{ c}⋅\vecs{ q} &=⟨0.25,0.25,0.50,0.20⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] &=314.5+85.5+1213+270.8 \\[4pt] &=1883.8. \end{align*}\]

Hivyo, AAA kulipwa $1,883.80 kwa vitu walivyouza. Faida yao, basi, hutolewa na

\[\vecs{ p}⋅\vecs{ q}−\vecs{ c}⋅\vecs{ q}=16267.5−1883.8 =14383.7. \nonumber \]

Kwa hiyo, AAA Party Supply Store alifanya $14,383.70 Mei.

Zoezi\(\PageIndex{6}\)

Mnamo Juni 1, AAA Party Supply Store iliamua kuongeza bei wanayochaji kwa ajili ya upendeleo wa chama hadi $2 kwa kila mfuko. Pia walibadilisha wauzaji kwa mialiko yao, na sasa wana uwezo wa kununua mialiko kwa 10 tu kwa kila mfuko. Gharama zao zote na bei zingine zinabaki sawa. Ikiwa AAA inauza mialiko 1408, neema za chama 147, mapambo ya 2112, na vitu vya huduma ya chakula vya 1894 mwezi wa Juni, tumia wadudu na bidhaa za dot kuhesabu mauzo yao ya jumla na faida kwa Juni.

Kidokezo

Tumia vectors nne-dimensional kwa gharama, bei, na kiasi kuuzwa.

Jibu

Mauzo = $15,685.50; faida = $14,073.15

Makadirio

Kama tulivyoona, kuongeza unachanganya vectors mbili ili kujenga vector matokeo. Lakini vipi ikiwa tunapewa vector na tunahitaji kupata sehemu zake za sehemu? Tunatumia makadirio ya vector kufanya mchakato kinyume; wanaweza kuvunja vector katika vipengele vyake. Ukubwa wa makadirio ya vector ni makadirio ya scalar. Kwa mfano, kama mtoto ni kuunganisha kushughulikia gari kwa pembeni 55°, tunaweza kutumia makadirio kuamua ni kiasi gani cha nguvu juu ya kushughulikia ni kweli kusonga gari mbele (\(\PageIndex{6}\)). Tunarudi kwenye mfano huu na kujifunza jinsi ya kutatua baada ya kuona jinsi ya kuhesabu makadirio.

Kielelezo\(\PageIndex{6}\): Wakati mtoto akichota gari, sehemu tu ya usawa ya nguvu husababisha gari mbele.

Ufafanuzi: Vector na Project

makadirio vector ya\(\vecs{ v}\) onto\(\vecs{ u}\) ni vector kinachoitwa\(\text{proj}_\vecs{ u}\vecs{ v}\) katika Kielelezo\(\PageIndex{7}\). Ina sawa hatua ya awali kama\(\vecs{ u}\) na\(\vecs{ v}\) na mwelekeo sawa na\(\vecs{ u}\), na inawakilisha sehemu ya\(\vecs{ v}\) kwamba vitendo katika mwelekeo wa\(\vecs{ u}\). Ikiwa\(θ\) inawakilisha angle kati\(\vecs{ u}\) na\(\vecs{ v}\), basi, kwa mali ya pembetatu, tunajua urefu wa\(\text{proj}_\vecs{ u}\vecs{ v}\) ni\(\|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs{ v}‖\cos θ.\) Wakati wa kuelezea\(\cos θ\) kwa suala la bidhaa ya dot, hii inakuwa

\[ \|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs v‖\cos θ=‖\vecs{ v}‖\left(\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}\right)=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖.} \nonumber \]

Sasa tunazidisha na vector kitengo katika mwelekeo wa\(\vecs{ u}\) kupata\(\text{proj}_\vecs{ u}\vecs{ v}\):

\[\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\left(\dfrac{1}{‖\vecs{ u}‖}\vecs{ u}\right)=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}. \nonumber \]

Urefu wa vector hii pia unajulikana kama makadirio ya scalar ya\(\vecs{ v}\) onto\(\vecs{ u}\) na inaashiria

\[\|\text{proj}_\vecs{ u}\vecs{ v}\|=\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖.} \nonumber \]

Kielelezo\(\PageIndex{7}\): makadirio ya\(\vecs{ v}\) onto\(\vecs{ u}\) inaonyesha sehemu ya vector\(\vecs{ v}\) katika mwelekeo wa\(\vecs{ u}\).

Mfano\(\PageIndex{7}\): Finding Projections

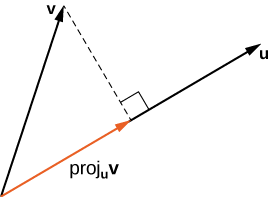
Kupata makadirio ya\(\vecs{ v}\) onto\(\vecs{ u}\).

1. \(\vecs{v}=⟨3,5,1⟩\)na\(\vecs{u}=⟨−1,4,3⟩\)
2. \(\vecs{v}=3\mathbf{\hat i}−2\mathbf{\hat j}\)na\(\vecs{u}=\mathbf{\hat i}+6\mathbf{\hat j}\)

Suluhisho

a Kubadilisha vipengele vya\(\vecs{ v}\) na\(\vecs{ u}\) ndani ya formula ya makadirio:

\[\begin{align*} \text{proj}_\vecs{ u}\vecs{ v} &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{⟨−1,4,3⟩⋅⟨3,5,1⟩}{∥⟨−1,4,3⟩∥^2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{−3+20+3}{(−1)^2+4^2+3^2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{20}{26}⟨−1,4,3⟩ \\[4pt] &=⟨−\dfrac{10}{13},\dfrac{40}{13},\dfrac{30}{13}⟩. \end{align*}\]

b Ili kupata makadirio mbili-dimensional, tu kukabiliana na formula kwa kesi mbili-dimensional:

\[\begin{align*} \text{proj}_\vecs{ u}\vecs{ v} &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{(\mathbf{\hat i}+6\mathbf{\hat j})⋅(3\mathbf{\hat i}−2\mathbf{\hat j})}{∥\mathbf{\hat i}+6\mathbf{\hat j}∥^2}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt] &= \dfrac{1(3)+6(−2)}{1^2+6^2}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt] &= −\dfrac{9}{37}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt] &= −\dfrac{9}{37}\mathbf{\hat i}−\dfrac{54}{37}\mathbf{\hat j}.\end{align*}\]

Wakati mwingine ni muhimu kuharibu vectors-yaani, kuvunja vector mbali kwa jumla. Utaratibu huu unaitwa azimio la vector katika vipengele. Makadirio yanatuwezesha kutambua vectors mbili za orthogonal zilizo na jumla ya taka. Kwa mfano, basi\(\vecs{ v}=⟨6,−4⟩\) na basi\(\vecs{ u}=⟨3,1⟩.\) Tunataka kuoza vector\(\vecs{ v}\) katika vipengele orthogonal kama kwamba moja ya vectors sehemu ina mwelekeo sawa na\(\vecs{ u}\).

Sisi kwanza kupata sehemu ambayo ina mwelekeo sawa na\(\vecs{ u}\) kwa projecting\(\vecs{ v}\) juu\(\vecs{ u}\). Hebu\(\vecs{ p}=\text{proj}_\vecs{ u}\vecs{ v}\). Kisha, tuna

\[\begin{align*}\vecs{ p} =\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] = \dfrac{18−4}{9+1}\vecs{ u} \\[4pt] = \dfrac{7}{5}\vecs{ u}=\dfrac{7}{5}⟨3,1⟩=⟨\dfrac{21}{5},\dfrac{7}{5}⟩. \end{align*}\]

Sasa fikiria vector\(\vecs{ q}=\vecs{ v}−\vecs{ p}.\) Tuna

\[\begin{align*} \vecs{ q} =\vecs{ v}−\vecs{ p} \\[4pt] = ⟨6,−4⟩−⟨\dfrac{21}{5},\dfrac{7}{5}⟩ \\[4pt] = ⟨\dfrac{9}{5},−\dfrac{27}{5}⟩. \end{align*}\]

Wazi, kwa njia ya sisi defined\(\vecs{ q}\), tuna\(\vecs{ v}=\vecs{ q}+\vecs{ p},\) na

\[\begin{align*}\vecs{ q}⋅\vecs{ p} =⟨\dfrac{9}{5},−\dfrac{27}{5}⟩⋅⟨\dfrac{21}{5},\dfrac{7}{5}⟩ \\[4pt] = \dfrac{9(21)}{25}+−\dfrac{27(7)}{25} \\[4pt] = \dfrac{189}{25}−\dfrac{189}{25}=0. \end{align*}\]

Kwa hiyo,\(\vecs{ q}\) na\(\vecs{ p}\) ni orthogonal.

Mfano\(\PageIndex{8}\): Resolving Vectors into Components

\(\vecs{ v}=⟨8,−3,−3⟩\)Eleza kama jumla ya vectors orthogonal kama kwamba moja ya wadudu ana mwelekeo sawa na\(\vecs{ u}=⟨2,3,2⟩.\)

Suluhisho

Hebu\(\vecs{ p}\) kuwakilisha makadirio ya\(\vecs{ v}\) kwenye\(\vecs{ u}\):

\[ \begin{align*} \vecs{ p} &=\text{proj}_\vecs{ u}\vecs{ v} \\[4pt] &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{⟨2,3,2⟩⋅⟨8,−3,−3⟩}{∥⟨2,3,2⟩∥^2}⟨2,3,2⟩ \\[4pt] &=\dfrac{16−9−6}{2^2+3^2+2^2}⟨2,3,2⟩ \\[4pt] &=\dfrac{1}{17}⟨2,3,2⟩ \\[4pt] &=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩. \end{align*} \nonumber \]

Kisha,

\[ \begin{align*} \vecs{ q} &=\vecs{ v}−\vecs{ p}=⟨8,−3,−3⟩−⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩\\[4pt] &=⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩. \end{align*} \nonumber \]

Kuangalia kazi yetu, tunaweza kutumia bidhaa ya dot ili kuthibitisha kuwa\(\vecs{ p}\) na\(\vecs{ q}\) ni vectors orthogonal:

\[ \begin{align*}\vecs{ p}⋅\vecs{ q}&=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩⋅⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩\\[4pt] &=\dfrac{268}{289}−\dfrac{162}{289}−\dfrac{106}{289}=0. \end{align*} \nonumber \]

Kisha,

\[\vecs{ v}=\vecs{ p}+\vecs{ q}=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩+⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩. \nonumber \]

Zoezi\(\PageIndex{7}\)

Express\(\vecs{ v}=5\mathbf{\hat i}−\mathbf{\hat j}\) kama jumla ya vectors orthogonal kama kwamba moja ya wadudu ina mwelekeo sawa na\(\vecs{ u}=4\mathbf{\hat i}+2\mathbf{\hat j}\).

Kidokezo

Anza kwa kutafuta makadirio ya\(\vecs{ v}\) onto\(\vecs{ u}\).

Jibu

\(\vecs{ v}=\vecs{ p}+\vecs{ q},\)wapi\(\vecs{ p}=\dfrac{18}{5}\mathbf{\hat i}+\dfrac{9}{5}\mathbf{\hat j}\) na\(\vecs{ q}=\dfrac{7}{5}\mathbf{\hat i}−\dfrac{14}{5}\mathbf{\hat j}\)

Mfano\(\PageIndex{9}\): Scalar Projection of Velocity

chombo meli majani bandari kusafiri\(15°\) kaskazini ya mashariki. Injini yake inazalisha kasi ya ncha 20 kando ya njia hiyo (angalia takwimu inayofuata). Aidha, sasa bahari huenda meli kaskazini mashariki kwa kasi ya ncha 2. Kuzingatia inji zote mbili na ya sasa, ni kasi gani meli inahamia katika mwelekeo\(15°\) kaskazini mwa mashariki? Pindua jibu kwa maeneo mawili ya decimal.

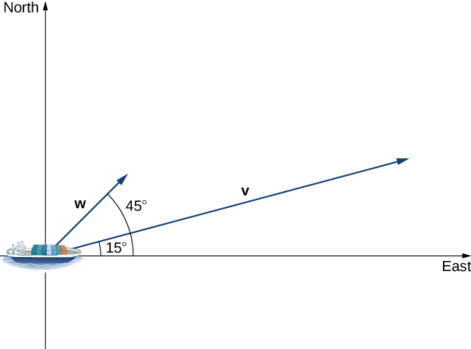
Suluhisho

Hebu\(\vecs{ v}\) kuwa vector kasi yanayotokana na inji, na basi\(\vecs{w}\) iwe vector kasi ya sasa. Tayari tunajua\(‖\vecs{ v}‖=20\) kando ya njia inayotaka. Tunahitaji tu kuongeza katika makadirio ya scalar ya\(\vecs{ w}\) onto\(\vecs{ v}\). Tunapata

\[ \begin{align*} \text{comp}_\vecs{ v}\vecs{ w}=\dfrac{\vecs{ v}⋅\vecs{ w}}{‖\vecs{ v}‖} \\[4pt] =\dfrac{‖\vecs{ v}‖‖\vecs{ w}‖\cos(30°)}{‖\vecs{ v}‖} =‖\vecs{ w}‖\cos(30°) =2\dfrac{\sqrt{3}}{2}=\sqrt{3}≈1.73\,\text{knots.}\end{align*}\]

Meli inahamia katika mafundo 21.73 katika mwelekeo\(15°\) kaskazini mwa mashariki.

Zoezi\(\PageIndex{8}\)

Kurudia mfano uliopita, lakini kudhani bahari ya sasa ni kusonga kusini mashariki badala ya kaskazini mashariki, kama inavyoonekana katika takwimu zifuatazo.

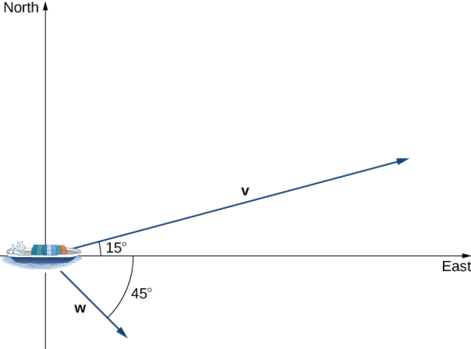
Kidokezo

Compute makadirio scalar ya\(\vecs{ w}\) onto\(\vecs{ v}\).

Jibu

21 mafundo

Kazi

Sasa kwa kuwa tunaelewa bidhaa za dot, tunaweza kuona jinsi ya kuzitumia kwa hali halisi ya maisha. Matumizi ya kawaida ya bidhaa ya dot ya vectors mbili ni katika hesabu ya kazi.

Kutoka fizikia, tunajua kwamba kazi imefanywa wakati kitu kinahamishwa na nguvu. Wakati nguvu ni mara kwa mara na kutumika katika mwelekeo huo kitu hatua, basi sisi kufafanua kazi kufanyika kama bidhaa ya nguvu na umbali kitu safari:\(W=Fd\). Tuliona mifano kadhaa ya aina hii katika sura za awali. Sasa fikiria mwelekeo wa nguvu ni tofauti na mwelekeo wa mwendo, kama ilivyo kwa mfano wa mtoto kuunganisha gari. Ili kupata kazi iliyofanyika, tunahitaji kuzidisha sehemu ya nguvu inayofanya kazi kwa uongozi wa mwendo kwa ukubwa wa uhamisho. Bidhaa ya dot inatuwezesha kufanya hivyo tu. Ikiwa tunawakilisha nguvu iliyotumiwa\(\vecs{ F}\) na vector na uhamisho wa kitu kwa vector\(\vecs{ s}\), basi kazi iliyofanywa na nguvu ni bidhaa ya dot\(\vecs{ F}\) na\(\vecs{ s}\).

Ufafanuzi: Nguvu ya kudumu

Wakati nguvu ya mara kwa mara inatumiwa kwenye kitu hivyo kitu kinaendelea kwenye mstari wa moja kwa moja kutoka hatua\(P\) hadi hatua\(Q\), kazi\(W\) iliyofanywa na nguvu\(\vecs{ F}\), inayofanya kwa pembe kutoka mstari wa mwendo, hutolewa na

\[W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ. \nonumber \]

Hebu tupate tena tatizo la gari la mtoto lililoanzishwa mapema. Tuseme mtoto anavuta gari na nguvu yenye ukubwa wa lb 8 kwenye kushughulikia kwa pembe ya 55°. Ikiwa mtoto huchota gari 50 ft, pata kazi iliyofanywa na nguvu (Kielelezo\(\PageIndex{8}\)).

Kielelezo\(\PageIndex{8}\): Sehemu ya usawa ya nguvu ni makadirio ya\(\vecs{ F}\) kwenye\(x\) mhimili mzuri.

Tuna

\[W=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ=8(50)(\cos(55°))≈229\,\text{ft⋅lb.} \nonumber \]

Katika vitengo vya kawaida vya Marekani, tunapima ukubwa wa nguvu\(∥\vecs{ F}∥\) katika paundi. Ukubwa wa vector ya uhamisho\(∥\vecd{PQ}∥\) hutuambia jinsi kitu kilichohamia, na kinapimwa kwa miguu. Kitengo cha kimila cha kipimo cha kazi, basi, ni pound-pound. Pound moja ya mguu ni kiasi cha kazi kinachohitajika kuhamisha kitu kilicho na uzito wa lb 1 umbali wa ft 1 moja kwa moja juu. Katika mfumo wa metri, kitengo cha kipimo cha nguvu ni newton (N), na kitengo cha kipimo cha ukubwa wa kazi ni mita ya newton (N · m), au joule (J).

Mfano\(\PageIndex{10}\): Calculating Work

Ukanda wa conveyor huzalisha nguvu\(\vecs{ F}=5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k}\) inayohamisha suti kutoka hatua\((1,1,1)\) hadi hatua\((9,4,7)\) kwenye mstari wa moja kwa moja. Pata kazi iliyofanywa na ukanda wa conveyor. Umbali hupimwa kwa mita na nguvu hupimwa katika newtons.

Suluhisho

Vector ya uhamisho\(\vecd{PQ}\) ina hatua ya awali\((1,1,1)\) na hatua ya mwisho\((9,4,7)\):

\[\vecd{PQ}=⟨9−1,4−1,7−1⟩=⟨8,3,6⟩=8\mathbf{\hat i}+3\mathbf{\hat j}+6\mathbf{\hat k}. \nonumber \]

Kazi ni bidhaa ya dot ya nguvu na uhamisho:

\[\begin{align*} W &=\vecs{ F}⋅\vecd{PQ} \\[4pt] &= (5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k})⋅(8\mathbf{\hat i}+3\mathbf{\hat j}+6\mathbf{\hat k}) \\[4pt] = 5(8)+(−3)(3)+1(6) \\[4pt] &=37\,\text{N⋅m} \\[4pt] &= 37\,\text{J} \end{align*}\]

Zoezi\(\PageIndex{9}\)

Nguvu ya mara kwa mara ya 30 lb inatumika kwa pembe ya 60° ili kuvuta mkoba wa mkono 10 ft ardhini. Kazi iliyofanywa na nguvu hii ni nini?

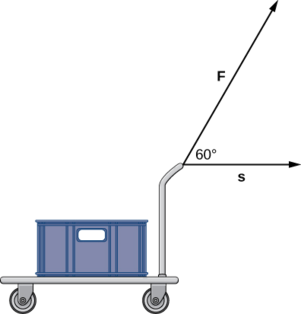
Kidokezo

Tumia ufafanuzi wa kazi kama bidhaa ya dot ya nguvu na umbali.

Jibu

150 ft-lb

Dhana muhimu

• bidhaa dot, au bidhaa scalar, ya wadudu wawili\(\vecs{ u}=⟨u_1,u_2,u_3⟩\) na\(\vecs{ v}=⟨v_1,v_2,v_3⟩\) ni\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3\).
• Bidhaa ya dot inatimiza mali zifuatazo:
  • \(\vecs{ u}⋅\vecs{ v}=\vecs{ v}⋅\vecs{ u}\)
  • \(\vecs{ u}⋅(\vecs{ v}+\vecs{ w})=\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ w}\)
  • \(c(\vecs{ u}⋅\vecs{ v})=(c\vecs{ u})⋅\vecs{ v}=\vecs{ u}⋅(c\vecs{ v})\)
  • \(\vecs{ v}⋅\vecs{ v}=‖\vecs{ v}‖^2\)
• Bidhaa ya dot ya vectors mbili inaweza kuelezwa, vinginevyo, kama Aina\(\vecs{ u}⋅\vecs{ v}=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ.\) hii ya bidhaa ya dot ni muhimu kwa kutafuta kipimo cha angle kilichoundwa na vectors mbili.
• Vectors\(\vecs{ u}\) na\(\vecs{ v}\) ni orthogonal kama\(\vecs{ u}⋅\vecs{ v}=0\).
• Pembe zilizoundwa na vector isiyo ya zero na axes za kuratibu huitwa pembe za mwelekeo kwa vector. Cosines ya pembe hizi hujulikana kama cosines ya mwelekeo.
• Makadirio ya vector ya\(\vecs{ v}\) onto\(\vecs{ u}\) ni vector\(\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}\). Ukubwa wa vector hii inajulikana kama makadirio ya scalar ya\(\vecs{ v}\) onto\(\vecs{ u}\), iliyotolewa na\(\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\).
• Kazi imefanywa wakati nguvu inatumiwa kwenye kitu, na kusababisha uhamisho. Wakati nguvu inawakilishwa\(\vecs{ F}\) na vector na uhamisho unawakilishwa na vector\(\vecs{ s}\), basi kazi iliyofanywa\(W\) inatolewa na formula\(W=\vecs{ F}⋅\vecs{ s}=∥\vecs{ F}∥‖\vecs{ s}‖\cos θ.\)

Mlinganyo muhimu

• Dot bidhaa ya\(\vecs{ u}\) na\(\vecs{ v}\)

\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ\)

• Cosine ya angle iliyoundwa\(\vecs{ u}\) na\(\vecs{ v}\)

\(\cos θ=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}\)

• Vector makadirio ya\(\vecs{ v}\) juu\(\vecs{ u}\)

\(\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}\)

• Makadirio ya Scalar ya\(\vecs{ v}\) kwenye\(\vecs{ u}\)

\(\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\)

• Kazi iliyofanywa na nguvu ya\(\vecs{ F}\) kusonga kitu kupitia vector ya makazi\(\vecd{PQ}\)

\(W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ\)

faharasa

pembe za mwelekeo

pembe zilizoundwa na vector nonzero na axes kuratibu

mwelekeo cosines

cosines ya pembe zilizoundwa na vector isiyo ya zero na axes kuratibu

dot bidhaa au bidhaa scalar

\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3\)wapi\(\vecs{ u}=⟨u_1,u_2,u_3⟩\) na\(\vecs{ v}=⟨v_1,v_2,v_3⟩\)

makadirio ya scalar

ukubwa wa makadirio ya vector ya vector

wadudu orthogonal

vectors kwamba fomu angle haki wakati kuwekwa katika nafasi ya kiwango

makadirio ya v

sehemu ya vector inayofuata mwelekeo fulani

kazi iliyofanywa na nguvu

kazi kwa ujumla hufikiriwa kama kiasi cha nishati inachukua kuhamisha kitu; ikiwa tunawakilisha nguvu iliyotumiwa\(\vecs{ F}\) na vector na uhamisho wa kitu kwa vector\(\vecs{ s}\), basi kazi iliyofanywa na nguvu ni bidhaa ya dot\(\vecs{ F}\) na\(\vecs{ s}\).

Wachangiaji na Majina

• Template:ContribOpenStaxCalc
• edited for vector notation by Paul Seeburger