10.4: Kufanya kazi na Taylor Series
- Page ID
- 178140
- Andika maneno ya mfululizo wa binomial.
- Tambua upanuzi wa mfululizo wa Taylor wa kazi za kawaida.
- Kutambua na kutumia mbinu za kupata Taylor mfululizo kwa ajili ya kazi.
- Tumia mfululizo wa Taylor kutatua equations tofauti.
- Matumizi Taylor mfululizo kutathmini integrals yasiyo ya msingi.
Katika sehemu iliyotangulia, tulifafanua mfululizo wa Taylor na tulionyesha jinsi ya kupata mfululizo wa Taylor kwa kazi kadhaa za kawaida kwa kuhesabu wazi coefficients ya polynomials ya Taylor. Katika sehemu hii sisi kuonyesha jinsi ya kutumia wale Taylor mfululizo hupata Taylor mfululizo kwa ajili ya kazi nyingine. Kisha tunawasilisha maombi mawili ya kawaida ya mfululizo wa nguvu. Kwanza, tunaonyesha jinsi mfululizo wa nguvu unaweza kutumika kutatua equations tofauti. Pili, sisi kuonyesha jinsi nguvu mfululizo inaweza kutumika kutathmini integrals wakati antiderivative ya integrand haiwezi walionyesha katika suala la kazi ya msingi. Katika mfano mmoja, tunaona\(\displaystyle \int e^{−x^2}dx,\) muhimu ambayo hutokea mara kwa mara katika nadharia ya uwezekano.
Mfululizo wa Binomial
Lengo letu la kwanza katika sehemu hii ni kuamua mfululizo wa Maclaurin kwa kazi\( f(x)=(1+x)^r\) kwa namba zote halisi\( r\). Mfululizo wa Maclaurin kwa kazi hii unajulikana kama mfululizo wa binomial. Tunaanza kwa kuzingatia kesi rahisi:\( r\) ni integer isiyo na negative. Sisi kukumbuka kwamba, kwa\( r=0,\,1,\,2,\,3,\,4,\;f(x)=(1+x)^r\) inaweza kuandikwa kama
\[\begin{align*} f(x) &=(1+x)^0=1, \\[4pt] f(x) &=(1+x)^1=1+x, \\[4pt] f(x) &=(1+x)^2=1+2x+x^2, \\[4pt] f(x) &=(1+x)^3=1+3x+3x^2+x^3 \\[4pt] f(x) &=(1+x)^4=1+4x+6x^2+4x^3+x^4. \end{align*}\]
Maneno upande wa kulia yanajulikana kama upanuzi wa binomial na coefficients hujulikana kama coefficients binomial. Kwa ujumla, kwa integer yoyote isiyo ya hasi\( r\), mgawo wa\( x^n\) binomial wa upanuzi wa binomial\( (1+x)^r\) hutolewa na
\[\binom{r}{n}=\dfrac{r!}{n!(r−n)!}\label{eq6.6} \]
na
\ [kuanza {align} f (x) &= (1+x) ^r\ nonumber\\ [5pt]
&=\ binom {r} {0} +\ binom {r} {1} x+\ binom {r} {2} x ^ 2+\ binom {r} {3} x ^ 3++\ binom {r} x ^ {-1} +\ binom {r} {r} x ^ r\ nonumber\\ [5pt]
&=\ sum_ {n = 0} ^r\ binom {r} {n} x ^ n.\ studio {eq6.7}\ mwisho {align}\]
Kwa mfano, kwa kutumia formula hii kwa\( r=5\), tunaona kwamba
\[ \begin{align*} f(x) &=(1+x)^5 \\[4pt] &=\binom{5}{0}1+\binom{5}{1}x+\binom{5}{2}x^2+\binom{5}{3}x^3+\binom{5}{4}x^4+\binom{5}{5}x^5 \\[4pt] &=\dfrac{5!}{0!5!}1+\dfrac{5!}{1!4!}x+\dfrac{5!}{2!3!}x^2+\dfrac{5!}{3!2!}x^3+\dfrac{5!}{4!1!}x^4+\dfrac{5!}{5!0!}x^5 \\[4pt] &=1+5x+10x^2+10x^3+5x^4+x^5. \end{align*}\]
Sisi sasa kufikiria kesi wakati exponent\(r.\)
ni idadi yoyote halisi, si lazima integer nonhegative. Ikiwa\(r\) sio integer isiyo ya kawaida, basi\(f(x)=(1+x)^r\) haiwezi kuandikwa kama polynomial ya mwisho. Hata hivyo, tunaweza kupata mfululizo wa nguvu kwa\(f\). Hasa, tunatafuta mfululizo wa Maclaurin\(f\). Ili kufanya hivyo, tunapata derivatives ya\(f\) na kutathmini yao katika\(x=0\).
\[ \begin{align*} f(x) &=(1+x)^r & f(0) &=1 \\[4pt] f′(x) &=r(1+x)^{r−1} & f'(0) &=r \\[4pt] f''(x) &=r(r−1)(1+x)^{r−2} & f''(0) &=r(r−1) \\[4pt] f'''(x) &=r(r−1)(r−2)(1+x)^{r−3} & f'''(0) &=r(r−1)(r−2) \\[4pt] f^{(n)}(x) &=r(r−1)(r−2)⋯(r−n+1)(1+x)^{r−n} & f^{(n)}(0) &=r(r−1)(r−2)⋯(r−n+1) \end{align*}\]
Tunahitimisha kuwa coefficients katika mfululizo wa binomial hutolewa na
\[\dfrac{f^{(n)}(0)}{n!}=\dfrac{r(r−1)(r−2)⋯(r−n+1)}{n!}.\label{eq6.8} \]
Tunaona kwamba ikiwa\(r\) ni integer isiyo na negative, basi\((r+1)^{\text{st}}\) derivative\( f^{(r+1)}\) ni kazi ya sifuri, na mfululizo umekoma. Kwa kuongeza, ikiwa\( r\) ni integer isiyo na hasi, basi Equation\ ref {eq6.8} kwa coefficients inakubaliana na Equation\ ref {eq6.6} kwa coefficients, na formula ya mfululizo wa binomial inakubaliana na Equation\ ref {eq6.7} kwa upanuzi wa mwisho wa binomial. Kwa ujumla, kutaja coefficients binomial kwa idadi yoyote halisi\( r\), tunafafanua
\[\binom{r}{n}=\dfrac{(r−1)(r−2)⋯(r−n+1)}{n!}. \nonumber \]
Kwa nukuu hii, tunaweza kuandika mfululizo wa binomial kwa\( (1+x)^r\) kama
\[\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+\dfrac{r(r−1)⋯(r−n+1)}{n!}x^n+⋯. \label{bin1} \]
Sasa tunahitaji kuamua muda wa kuunganisha kwa mfululizo wa binomial Equation\ ref {bin1}. Tunatumia mtihani wa uwiano. Kwa hiyo, tunaona
\[\begin{align*} \dfrac{|a_{n+1}|}{|a_n|} &=\dfrac{|r(r−1)(r−2)⋯(r−n)|x||^{n+1}}{(n+1)!}⋅\dfrac{n}{|r(r−1)(r−2)⋯(r−n+1)||x|^n} \\[4pt] &=\dfrac{|r−n||x|}{|n+1|} \end{align*}\].
Tangu
\[\lim_{n→∞}\dfrac{|a_{n+1}|}{|a_n|}=|x|<1 \nonumber \]
ikiwa na tu ikiwa\( |x|<1\), tunahitimisha kuwa muda wa kuunganisha kwa mfululizo wa binomial ni\( (−1,1)\). Tabia katika mwisho wa mwisho inategemea\( r\). Inaweza kuonyeshwa kuwa kwa mfululizo\( r≥0\) hujiunga katika mwisho wote; kwa\( −1<r<0\), mfululizo hujiunga\( x=1\) na hutofautiana\( x=−1\); na kwa\( r<−1\), mfululizo hupungua katika mwisho wote. Mfululizo wa binomial unajiunga na namba zote halisi\( r\), lakini kuthibitisha ukweli huu kwa kuonyesha kwamba salio\( R_n(x)→0\) ni vigumu.\( (1+x)^r\)\( (−1,1)\)
Kwa idadi yoyote halisi\( r\), mfululizo wa Maclaurin\( f(x)=(1+x)^r\) ni mfululizo wa binomial. Ni hujiunga na\( f\) kwa\( |x|<1\), na tunaandika
\[(1+x)^r=\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+r\dfrac{(r−1)⋯(r−n+1)}{n!}x^n+⋯ \nonumber \]
kwa\( |x|<1\).
Tunaweza kutumia ufafanuzi huu kupata mfululizo binomial kwa\( f(x)=\sqrt{1+x}\) na kutumia mfululizo kwa takriban\( \sqrt{1.5}\).
- Kupata mfululizo binomial kwa\( f(x)=\sqrt{1+x}\).
- Tumia utaratibu wa tatu Maclaurin polynomial\( p_3(x)\) ili kukadiria\( \sqrt{1.5}\). Matumizi theorem Taylor ya kufungwa makosa. Tumia matumizi ya graphing kulinganisha grafu ya\( f\) na\( p_3\).
Suluhisho
a. hapa\( r=\dfrac{1}{2}\). Kutumia ufafanuzi wa mfululizo wa binomial, tunapata
\ (\ displaystyle\ quad\ kuanza {align*}\ sqrt {1+x} &=1+\ drac {1} {2} x+\ drac {(1/2) (-1/2)} {2!} x ^ 2+\ dfrac {(1/2) (-1/2) (-3/2)} {3!} x^ 3+\\ [5pt]
&=1+\ dfrac {1} {2} {2}\ drac {1} {2!} \ dfrac {1} {2 ^ 2} x^2+\ dfrac {1} {3!} \ dfrac {13} {2^3} x^3—+\ dfrac {(-1) ^ {n+1}} {n!} \ dfrac {135( 2n-1)} {2^n} x ^ n+\\ [5pt]
&=1+\ sum_ {n=1} ^Δ\ dfrac {(-1) ^ {n+1}} {n!} \ dfrac {135( 2n-3)} {2^n} x ^ n.\ mwisho {align*}\)
b Kutokana na matokeo katika sehemu a. tatu ili Maclaurin polynomial ni
\( p_3(x)=1+\dfrac{1}{2}x−\dfrac{1}{8}x^2+\dfrac{1}{16}x^3\).
Kwa hiyo,
\( \sqrt{1.5}=\sqrt{1+0.5}≈1+\dfrac{1}{2}(0.5)−\dfrac{1}{8}(0.5)^2+\dfrac{1}{16}(0.5)^3≈1.2266.\)
Kutoka kwa theorem ya Taylor, hitilafu inatimiza
\( R_3(0.5)=\dfrac{f^{(4)}(c)}{4!}(0.5)^4\)
kwa baadhi\( c\) kati\( 0\) na\( 0.5\). Tangu\( f^{(4)}(x)=−\dfrac{15}{2^4(1+x)^{7/2}}\), na thamani ya\( ∣f^{(4)}(x)∣\) juu ya muda\( (0,0.5)\) hutokea katika\( x=0\), tuna
\( |R_3(0.5)|≤\dfrac{15}{4!2^4}(0.5)^4≈0.00244.\)
Kazi na polynomial Maclaurin\( p_3\) ni graphed katika Kielelezo\(\PageIndex{1}\).
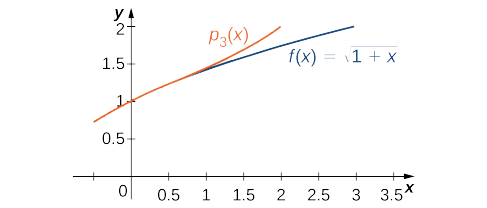
Kupata mfululizo binomial kwa\( f(x)=\dfrac{1}{(1+x)^2}\).
- Kidokezo
-
Tumia ufafanuzi wa mfululizo wa binomial kwa\( r=−2\).
- Jibu
-
\(\displaystyle \sum_{n=0}^∞(−1)^n(n+1)x^n\)
Kazi za kawaida zilionyesha kama Taylor Series
Kwa hatua hii, tumepata mfululizo wa Maclaurin kwa kazi za kielelezo, trigonometric, na logarithmic, pamoja na kazi za fomu\( f(x)=(1+x)^r\). Katika Jedwali\(\PageIndex{1}\), sisi muhtasari matokeo ya mfululizo huu. Tunasema kuwa muunganiko wa mfululizo wa Maclaurin kwa\( f(x)=\ln(1+x)\) mwisho\( x=1\) na mfululizo wa Maclaurin kwa\( f(x)=\tan^{−1}x\) mwisho\( x=1\) na\( x=−1\) hutegemea theorem ya juu zaidi kuliko sisi sasa hapa. (Rejea theorem Abel kwa ajili ya majadiliano ya hatua hii zaidi ya kiufundi.)
| Kazi | Maclaurin mfululizo | Muda wa Muungano |
|---|---|---|
| \( f(x)=\dfrac{1}{1−x}\) | \(\displaystyle \sum_{n=0}^∞x^n\) | \( −1<x<1\) |
| \( f(x)=e^x\) | \(\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}\) | \( −∞<x<∞\) |
| \( f(x)=\sin x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{(2n+1)!}\) | \( −∞<x<∞\) |
| \( f(x)=\cos x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n}}{(2n)!}\) | \( −∞<x<∞\) |
| \( f(x)=\ln(1+x)\) | \(\displaystyle \sum_{n=0}^∞(−1)^{n+1}\dfrac{x^n}{n}\) | \( −1<x<1\) |
| \( f(x)=\tan^{−1}x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{2n+1}\) | \( −1<x<1\) |
| \( f(x)=(1+x)^r\) | \(\displaystyle \sum_{n=0}^∞\binom{r}{n}x^n\) | \( −1<x<1\) |
Mapema katika sura, tulionyesha jinsi unaweza kuchanganya mfululizo wa nguvu ili kuunda mfululizo mpya wa nguvu. Hapa tunatumia mali hizi, pamoja na mfululizo wa Maclaurin katika Jedwali\(\PageIndex{1}\), ili kuunda mfululizo wa Maclaurin kwa kazi nyingine.
Kupata Maclaurin mfululizo wa kila moja ya kazi zifuatazo kwa kutumia moja ya mfululizo waliotajwa katika Jedwali\(\PageIndex{1}\).
- \( f(x)=\cos\sqrt{x}\)
- \( f(x)=\sinh x\)
Suluhisho
a Kutumia mfululizo wa Maclaurin kwa\( \cos x\) tunaona kwamba mfululizo wa Maclaurin\( \cos\sqrt{x}\) hutolewa na
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^n(\sqrt{x})^{2n}}{(2n)!}=\sum_{n=0}^∞\dfrac{(−1)^nx^n}{(2n)!}=1−\dfrac{x}{2!}+\dfrac{x^2}{4!}−\dfrac{x^3}{6!}+\dfrac{x^4}{8!}−⋯.\)
Mfululizo huu hujiunga na\( \cos\sqrt{x}\) kwa wote\( x\) katika uwanja wa\( \cos\sqrt{x}\); yaani, kwa ajili ya wote\( x≥0\).
b Ili kupata mfululizo Maclaurin kwa\( \sinh x,\) sisi kutumia ukweli kwamba
\( \sinh x=\dfrac{e^x−e^{−x}}{2}.\)
Kutumia mfululizo wa Maclaurin\( e^x\), tunaona kwamba\(n^{\text{th}}\) neno katika mfululizo wa Maclaurin\(\sinh x\) hutolewa na
\( \dfrac{x^n}{n!}−\dfrac{(−x)^n}{n!}.\)
Kwa\( n\) hata, neno hili ni sifuri. Kwa\( n\) isiyo ya kawaida, neno hili ni\( \dfrac{2x^n}{n!}\). Kwa hiyo, mfululizo wa Maclaurin\(\sinh x\) una masharti yasiyo ya kawaida na hutolewa na
\(\displaystyle \sum_{n=0}^∞\dfrac{x^{2n+1}}{(2n+1)!}=x+\dfrac{x^3}{3!}+\dfrac{x^5}{5!}+⋯.\)
Pata mfululizo wa Maclaurin\( \sin(x^2).\)
- Kidokezo
-
Tumia mfululizo wa Maclaurin\( \sin x.\)
- Jibu
-
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^nx^{4n+2}}{(2n+1)!}\)
Pia tulionyesha hapo awali katika sura hii jinsi mfululizo wa nguvu unaweza kutofautishwa mrefu kwa muda ili kuunda mfululizo mpya wa nguvu. Katika Mfano\(\PageIndex{3}\), sisi kutofautisha mfululizo binomial kwa\( \sqrt{1+x}\) muda kwa muda ili kupata mfululizo binomial kwa\( \dfrac{1}{\sqrt{1+x}}\). Kumbuka kwamba tunaweza kujenga mfululizo binomial kwa\( \dfrac{1}{\sqrt{1+x}}\) moja kwa moja kutoka ufafanuzi, lakini kutofautisha mfululizo binomial kwa\( \sqrt{1+x}\) ni hesabu rahisi.
Kutumia mfululizo binomial\( \sqrt{1+x}\) kwa kupata mfululizo binomial kwa\( \dfrac{1}{\sqrt{1+x}}\).
Suluhisho
Kazi mbili zinahusiana na
\( \dfrac{d}{dx}\sqrt{1+x}=\dfrac{1}{2\sqrt{1+x}}\),
hivyo mfululizo wa binomial\( \dfrac{1}{\sqrt{1+x}}\) hutolewa na
\(\displaystyle \dfrac{1}{\sqrt{1+x}}=2\dfrac{d}{dx}\sqrt{1+x}=1+\sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n.\)
Pata mfululizo wa binomial\( f(x)=\dfrac{1}{(1+x)^{3/2}}\)
- Kidokezo
-
Tofautisha mfululizo kwa\( \dfrac{1}{\sqrt{1+x}}\)
- Jibu
-
\(\displaystyle \sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n\)
Katika mfano huu, tulifafanua mfululizo wa Taylor unaojulikana ili kujenga mfululizo wa Taylor kwa kazi nyingine. Uwezo wa kutofautisha mfululizo wa nguvu kwa muda huwafanya kuwa chombo chenye nguvu cha kutatua usawa tofauti. Sasa tunaonyesha jinsi hii inavyofanyika.
Kutatua Ulinganisho tofauti na Mfululizo wa Nguvu
Fikiria equation tofauti
\[y′(x)=y.\nonumber \]
Kumbuka kwamba hii ni equation ya kwanza ili kutenganishwa na ufumbuzi wake ni\(y=Ce^x\). Equation hii ni rahisi kutatuliwa kwa kutumia mbinu kujadiliwa mapema katika maandishi. Kwa equations tofauti zaidi, hata hivyo, hatuna zana za uchambuzi za kutatua. Mfululizo wa nguvu ni chombo muhimu sana cha kutatua aina nyingi za equations tofauti. Katika mbinu hii, tunatafuta suluhisho la fomu\(\displaystyle y=\sum_{n=0}^∞c_nx^n\) na kuamua nini coefficients ingehitaji kuwa. Katika mfano unaofuata, tunazingatia tatizo la thamani ya awali linalohusisha\(y′=y\) kuonyesha mbinu.
Tumia mfululizo wa nguvu ili kutatua tatizo la thamani ya awali\(y′=y,\quad y(0)=3.\)
Suluhisho
Tuseme kwamba kuna ufumbuzi wa mfululizo wa nguvu
\(\displaystyle y(x)=\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+⋯.\)
Kutofautisha mfululizo huu mrefu kwa muda, tunapata
\( y′=c_1+2c_2x+3c_3x^2+4c_4x^3+⋯.\)
Kama\(y\) satisfies equation tofauti, basi
\( c_0+c_1x+c_2x^2+c_3x^3+⋯=c_1+2c_2x+3c_3x^2+4c_3x^3+⋯.\)
Kutumia uwakilishi wa mfululizo wa nguvu, tunajua kwamba mfululizo huu unaweza kuwa sawa tu ikiwa coefficients yao ni sawa. Kwa hiyo,
\( c_0=c_1,\)
\( c_1=2c_2,\)
\( c_2=3c_3,\)
\( c_3=4c_4,\)
⋮
Kutumia hali ya awali\( y(0)=3\) pamoja na uwakilishi wa mfululizo wa nguvu
\( y(x)=c_0+c_1x+c_2x^2+c_3x^3+⋯\),
tunaona kwamba\( c_0=3\). Sasa tuko tayari kutatua kwa coefficients zote. Kutumia ukweli kwamba\( c_0=3\), tuna
\ [kuanza {align*} c_1&=c_0=3=\ dfrac {3} {1!} ,\\ [5pt]
c_2&=\ dfrac {c_1} {2} =\ dfrac {3} {2} =\ dfrac {3} {2!} ,\\ [5pt]
c_3&=\ dfrac {c_2} {3} =\ dfrac {3} {32} =\ dfrac {3} {3!} ,\\ [5pt]
c_4&=\ dfrac {c_3} {4} =\ dfrac {3} {432} =\ dfrac {3} {4!}. \ mwisho {align*}\]
Kwa hiyo,
\[y=3\left[1+\dfrac{1}{1!}x+\dfrac{1}{2!}x^2+\dfrac{1}{3!}x^3\dfrac{1}{4!}x^4+⋯\right]=3\sum_{n=0}^∞\dfrac{x^n}{n!}.\nonumber \]
Unaweza kutambua
\[\sum_{n=0}^∞\dfrac{x^n}{n!}\nonumber \]
kama Taylor mfululizo kwa\( e^x\). Kwa hiyo, suluhisho ni\( y=3e^x\).
Tumia mfululizo wa nguvu ili kutatua\( y′=2y,\quad y(0)=5.\)
- Kidokezo
-
Ulinganisho wa coefficients kadhaa za kwanza\( c_n\) zitakidhi\( c_0=2c_1,\,c_1=2⋅2c_2,\,c_2=2⋅3c_3,\,….\) Kwa ujumla, kwa wote\( n≥0,\;c_n=2(n+1)C_{n+1}\).
- Jibu
-
\( y=5e^{2x}\)
Sasa tunazingatia mfano unaohusisha usawa tofauti ambao hatuwezi kutatua kwa kutumia mbinu zilizojadiliwa hapo awali. Hii equation tofauti
\[y′−xy=0\nonumber \]
inajulikana kama equation Airy ya. Ina maombi mengi katika fizikia ya hisabati, kama mfano wa diffraction ya mwanga. Hapa tunaonyesha jinsi ya kutatua kwa kutumia mfululizo wa nguvu.
Tumia mfululizo wa nguvu kutatua\(y''−xy=0\) na hali ya awali\( y(0)=a\) na\( y'(0)=b.\)
Suluhisho
Tunatafuta suluhisho la fomu
\[y=\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+⋯\nonumber \]
Kutofautisha neno hili kazi kwa muda, tunapata
\ [kuanza {align*} y& =c_1+2c_2x+3c_3x^2+4c_4x^3+,\\ [4pt]
y"& =21c_2+32c_3x+43c_4x^2+2x+43c_4x^2+. \ mwisho {align*}\]
Kama\(y\) satisfies equation\( y''=xy\), basi
\( 2⋅1c_2+3⋅2c_3x+4⋅3c_4x^2+⋯=x(c_0+c_1x+c_2x^2+c_3x^3+⋯).\)
Kutumia [kiungo] juu ya uwakilishi wa mfululizo wa nguvu, tunajua kwamba coefficients ya shahada sawa lazima iwe sawa. Kwa hiyo,
\( 2⋅1c_2=0,\)
\( 3⋅2c_3=c_0,\)
\( 4⋅3c_4=c_1,\)
\( 5⋅4c_5=c_2,\)
⋮
Kwa ujumla zaidi, kwa\( n≥3\), tuna\( n⋅(n−1)c_n=c_{n−3}\). Kwa kweli, coefficients zote zinaweza kuandikwa kwa suala la\( c_0\) na\( c_1\). Ili kuona hili, kwanza kumbuka kuwa\( c_2=0\). Kisha
\( c_3=\dfrac{c_0}{3⋅2}\),
\( c_4=\dfrac{c_1}{4⋅3}\).
Kwa\( c_5,\,c_6,\,c_7\), tunaona kwamba
\ [kuanza {align*} c_5&=\ dfrac {c_2} {54} =0,\\ [5pt]
c_6&=\ dfrac {c_3} {65} =\ dfrac {c_0} {6532},\\ [5pt]
c_7&=\ dfrac {c_4} {76} =\ dfrac {c_1} {7643}. \ mwisho {align*}\]
Kwa hiyo, ufumbuzi wa mfululizo wa equation tofauti hutolewa na
\( y=c_0+c_1x+0⋅x^2+\dfrac{c_0}{3⋅2}x^3+\dfrac{c_1}{4⋅3}x^4+0⋅x^5+\dfrac{c_0}{6⋅5⋅3⋅2}x^6+\dfrac{c_1}{7⋅6⋅4⋅3}x^7+⋯.\)
Hali ya awali\( y(0)=a\) ina maana\( c_0=a\). Kutofautisha neno hili la mfululizo kwa muda na kutumia ukweli kwamba\( y′(0)=b\), tunahitimisha hilo\( c_1=b\).
Kwa hiyo, ufumbuzi wa tatizo hili la awali la thamani ni
\( y=a\left(1+\dfrac{x^3}{3⋅2}+\dfrac{x}{6⋅5⋅3⋅2}+⋯\right)+b\left(x+\dfrac{x^4}{4⋅3}+\dfrac{x^7}{7⋅6⋅4⋅3}+⋯\right).\)
Tumia mfululizo wa nguvu kutatua\( y''+x^2y=0\) na hali ya awali\( y(0)=a\) na\( y′(0)=b\).
- Kidokezo
-
Coefficients kukidhi\( c_0=a,\,c_1=b,\,c_2=0,\,c_3=0,\) na kwa\( n≥4,\; n(n−1)c_n=−c_{n−4}\).
- Jibu
-
\(y=a\left(1−\dfrac{x^4}{3⋅4}+\dfrac{x^8}{3⋅4⋅7⋅8}−⋯\right)+b\left(x−\dfrac{x^5}{4⋅5}+\dfrac{x^9}{4⋅5⋅8⋅9}−⋯\right)\)
Kutathmini Integrals yasiyo ya msingi
Kutatua equations tofauti ni matumizi ya kawaida ya mfululizo wa nguvu. Sasa tunageuka kwenye programu ya pili. Tunaonyesha jinsi mfululizo wa nguvu unaweza kutumika kutathmini integrals kuwashirikisha kazi ambazo antiderivatives haziwezi kuelezwa kwa kutumia kazi za msingi.
Moja muhimu ambayo hutokea mara nyingi katika maombi katika nadharia uwezekano ni\(\displaystyle \int e^{−x^2}\,dx.\) bahati mbaya, antiderivative ya integrand\( e^{−x^2}\) si kazi ya msingi. Kwa kazi ya msingi, tunamaanisha kazi ambayo inaweza kuandikwa kwa kutumia idadi ya mwisho ya mchanganyiko wa algebraic au nyimbo za kazi za kielelezo, logarithmic, trigonometric, au nguvu. Tunasema kwamba neno “kazi ya msingi” si sawa na kazi isiyo ngumu. Kwa mfano, kazi\( f(x)=\sqrt{x^2−3x}+e^{x^3}−\sin(5x+4)\) ni kazi ya msingi, ingawa si kazi rahisi sana. Yoyote muhimu ya fomu\(\displaystyle \int f(x)\,dx\) ambapo antiderivative ya\( f\) haiwezi kuandikwa kama kazi ya msingi ni kuchukuliwa yasiyo ya msingi muhimu.
integrals yasiyo ya msingi haiwezi tathmini kwa kutumia mbinu za msingi za ushirikiano zilizojadiliwa mapema. Njia moja ya kutathmini integrals vile ni kwa kuonyesha integrand kama mfululizo wa nguvu na kuunganisha muda kwa muda. Tunaonyesha mbinu hii kwa kuzingatia\(\displaystyle \int e^{−x^2}\,dx.\)
- Express\(\displaystyle \int e^{−x^2}dx\) kama mfululizo usio.
- \(\displaystyle \int ^1_0e^{−x^2}dx\)Kutathmini ndani ya makosa ya\( 0.01\).
Suluhisho
a Mfululizo wa Maclaurin\( e^{−x^2}\) hutolewa na
\ [kuanza {align*} e^ {-x^2} &=\ sum_ {n = 0} ^Δ\ dfrac {(-x^2) ^n} {n!} \\ [5pt]
&=1,1x^2+\ dfrac {x ^ 4} {2!} -\ dfrac {x^6} {3!} ++ (-1) ^n\ dfrac {x^ {2n}} {n!} +\\ [5pt]
&=\ sum_ {n = 0} ^Δ (-1) ^n\ dfrac {x^ {2n}} {n!}. \ mwisho {align*}\]
Kwa hiyo,
\ [kuanza {align*}\ int e^ {-x^2}\, dx&=\ int\ kushoto (1,1x^2+\ dfrac {x^4} {2!} -\ dfrac {x^6} {3!} ++ (-1) ^n\ dfrac {x^ {2n}} {n!} +\ haki)\, dx\\ [5pt]
&=C+X-\ dfrac {x^3} {3} +\ dfrac {x^5} {5.2!} -\ dfrac {x^7} {7.3!} ++ (-1) ^n\ dfrac {x^ {2n+1}} {(2n+1) n!} +. \ mwisho {align*}\]
b Kutumia matokeo kutoka kwa sehemu a. tuna
\[ \int ^1_0e^{−x^2}\,dx=1−\dfrac{1}{3}+\dfrac{1}{10}−\dfrac{1}{42}+\dfrac{1}{216}−⋯.\nonumber \]
Jumla ya masharti manne ya kwanza ni takriban\( 0.74\). Kwa mtihani wa mfululizo wa mfululizo, makadirio haya ni sahihi kwa ndani ya kosa la chini\( \dfrac{1}{216}≈0.0046296<0.01.\)
Express\(\displaystyle \int \cos\sqrt{x}\,dx\) kama mfululizo usio. \(\displaystyle \int ^1_0\cos\sqrt{x}\,dx\)Kutathmini ndani ya makosa ya\( 0.01\).
- Kidokezo
-
Tumia mfululizo uliopatikana katika Mfano\(\PageIndex{6}\).
- Jibu
-
\(\displaystyle C+\sum_{n=1}^∞(−1)^{n+1}\dfrac{x^n}{n(2n−2)!}\)muhimu uhakika ni takriban\( 0.514\) ndani ya makosa ya\( 0.01\).
Kama ilivyoelezwa hapo juu, muhimu\(\displaystyle \int e^{−x^2}\,dx\) hutokea mara nyingi katika nadharia ya uwezekano. Hasa, hutumiwa wakati wa kusoma seti za data ambazo zinawasambazwa kwa kawaida, maana ya maadili ya data yanalala chini ya pembe ya kengele-umbo. Kwa mfano, ikiwa seti ya maadili ya data ni kawaida kusambazwa kwa kupotoka kwa maana\( μ\) na kiwango\( σ\), basi uwezekano kwamba thamani iliyochaguliwa kwa nasibu iko kati\( x=a\) na\( x=b\) hutolewa na
\[\dfrac{1}{σ\sqrt{2π}}\int ^b_ae^{−(x−μ)^2/(2σ^2)}\,dx.\label{probeq} \]
(Angalia Kielelezo\(\PageIndex{2}\).)
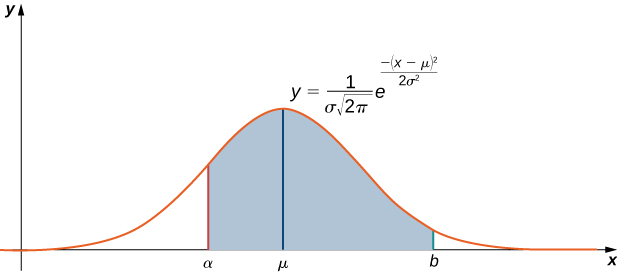
Ili kurahisisha hii muhimu, sisi kawaida basi\( z=\dfrac{x−μ}{σ}\). Kiasi hiki\(z\) kinajulikana kama\(z\) alama ya thamani ya data. Kwa kurahisisha hii, Equation muhimu\ ref {probeq} inakuwa
\[\dfrac{1}{\sqrt{2π}}\int ^{(b−μ)/σ}_{(a−μ)/σ}e^{−z^2/2}\,dz. \nonumber \]
Katika Mfano\(\PageIndex{7}\), tunaonyesha jinsi tunaweza kutumia hii muhimu katika kuhesabu probabilities.
Tuseme seti ya alama sanifu mtihani ni kawaida kusambazwa kwa wastani\( μ=100\) na kiwango kupotoka\( σ=50\). Matumizi Equation\ ref {probeq} na kwanza maneno sita katika mfululizo Maclaurin\( e^{−x^2/2}\) kwa takriban uwezekano kwamba nasibu kuchaguliwa mtihani alama ni kati\( x=100\) na\( x=200\). Matumizi alternating mfululizo mtihani kuamua jinsi sahihi makadirio yako ni.
Suluhisho
Tangu\( μ=100,σ=50,\) na sisi ni kujaribu kuamua eneo chini ya Curve kutoka\( a=100\) kwa\( b=200\), muhimu Equation\ ref {probeq} inakuwa
\[ \dfrac{1}{\sqrt{2π}}\int ^2_0e^{−z^2/2}\,dz.\nonumber \]
Mfululizo wa Maclaurin\( e^{−x^2/2}\) hutolewa na
\ [kuanza {align*} e^ {-x^2/2} &=\ sum_ {n = 0} ^Δ\ dfrac {\ kushoto (\ dfrac {x^2} {2}\ haki) ^n} {n!} \\ [5pt]
&=1-\ dfrac {x^2} {2^11!} +\ dfrac {x ^ 4} {2^22!} -\ dfrac {x^6} {2^33!} ++ (-1) ^n\ dfrac {x^ {2n}} {2^nn}! +\\ [5pt]
&=\ sum_ {n = 0} ^Δ (-1) ^n\ dfrac {x^ {2n}} {2^nn!}. \ mwisho {align*}\]
Kwa hiyo,
\ [kuanza {align*}\ dfrac {1} {\ sqrt {2π}}\ int e^ {-z^2/2}\, dz&=\ dfrac {1} {\ sqrt {2π}}\ int\ kushoto (1 -\ dfrac {z ^ 2} {2^11!} +\ dfrac {z ^ 4} {2^22!} -\ dfrac {z ^ 6} {2^33!} ++ (-1) ^n\ dfrac {z^ {2n}} {2^nn!} +\ kulia) dz\\ [5pt]
&=\ dfrac {1} {\ sqrt {2π}}\ kushoto (C+Z\\ dfrac {z ^ 3} {32^11!} +\ dfrac {z ^ 5} {52^22!} -\ dfrac {z ^ 7} {72^33!} ++ (-1) ^n\ dfrac {z^ {2n+1}} {(2n+1) 2^nn!} +\ haki)\ mwisho {align*}\]
\[\dfrac{1}{\sqrt{2π}}\int ^2_0e^{−z^2/2}\,dz=\dfrac{1}{\sqrt{2π}}\left(2−\dfrac{8}{6}+\dfrac{32}{40}−\dfrac{128}{336}+\dfrac{512}{3456}−\dfrac{2^{11}}{11⋅2^5⋅5!}+⋯\right)\nonumber \]
Kutumia maneno matano ya kwanza, tunakadiria kuwa uwezekano ni takriban 0.4922. Kwa mtihani wa mfululizo wa mfululizo, tunaona kwamba makadirio haya ni sahihi kwa ndani
\[ \dfrac{1}{\sqrt{2π}}\dfrac{2^{13}}{13⋅2^6⋅6!}≈0.00546.\nonumber \]
Uchambuzi
Kama wewe ni ukoo na nadharia uwezekano, unaweza kujua kwamba uwezekano kwamba thamani data ni ndani ya mbili kupotoka kiwango cha maana ni takriban\( 95\%.\) Hapa sisi mahesabu uwezekano kwamba thamani data ni kati ya wastani na mbili kupotoka kiwango juu ya wastani, hivyo makadirio lazima karibu\( 47.5\%\). Makadirio, pamoja na kufungwa kwa usahihi, huanguka ndani ya aina hii.
Matumizi ya kwanza suala tano ya mfululizo Maclaurin kwa\( e^{−x^2/2}\) kukadiria uwezekano kwamba nasibu kuchaguliwa mtihani alama ni kati\( 100\) na\( 150\). Tumia mtihani wa mfululizo wa kubadilisha ili ueleze usahihi wa makadirio haya.
- Kidokezo
-
\(\displaystyle \int ^1_0e^{−z^2/2}\,dz\)Kutathmini kutumia kwanza maneno tano ya mfululizo Maclaurin kwa\( e^{−z^2/2}\).
- Jibu
-
makadirio ni takriban makadirio\( 0.3414.\) Hii ni sahihi kwa ndani\( 0.0000094.\)
Programu nyingine ambayo sehemu isiyo ya msingi hutokea inahusisha kipindi cha pendulum. Muhimu ni
\[\int ^{π/2}_0\dfrac{dθ}{\sqrt{1−k^2\sin^2θ}}\nonumber \].
Muhimu wa fomu hii inajulikana kama muhimu ya elliptic ya aina ya kwanza. Vipengele vya elliptic awali viliondoka wakati wa kujaribu kuhesabu urefu wa arc wa ellipse. Sasa tunaonyesha jinsi ya kutumia mfululizo wa nguvu ili takriban hii muhimu.
Kipindi cha pendulum ni wakati unachukua kwa pendulum kufanya swing moja kamili ya kurudi nyuma. Kwa pendulum na urefu\( L\) ambao hufanya angle ya juu\( θ_{max}\) na wima, kipindi chake\( T\) kinatolewa na
\[ T=4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\dfrac{dθ}{\sqrt{1−k^2\sin^2θ}}\nonumber \]
\( g\)wapi kasi kutokana na mvuto na\( k=\sin\left(\dfrac{θ_{max}}{2}\right)\) (angalia Kielelezo\(\PageIndex{3}\)). (Tunaona kwamba formula hii kwa kipindi hicho inatokana na mfano usio na mstari wa pendulum. Katika baadhi ya matukio, kwa kurahisisha, mfano wa linearized\(\sin θ\) hutumiwa na unakadiriwa na\( θ\).)
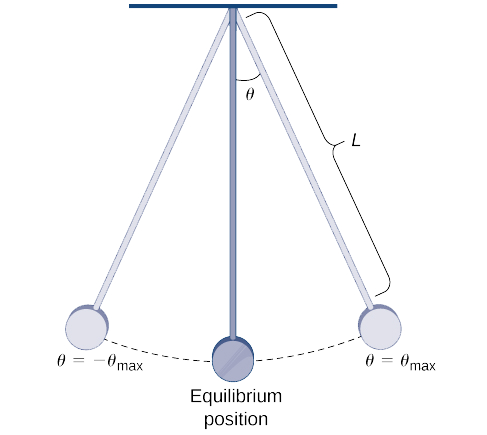
Tumia mfululizo wa binomial
\[ \dfrac{1}{\sqrt{1+x}}=1+\sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n\nonumber \]
kukadiria kipindi cha pendulum hii. Hasa, takriban kipindi cha pendulum kama
- unatumia muda wa kwanza tu katika mfululizo wa binomial, na
- unatumia maneno mawili ya kwanza katika mfululizo wa binomial.
Suluhisho
Tunatumia mfululizo wa binomial, kuchukua nafasi ya x na\( −k^2\sin^2θ.\) Kisha tunaweza kuandika kipindi kama
\[ T=4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\left(1+\dfrac{1}{2}k^2\sin^2θ+\dfrac{1⋅3}{2!2^2}k^4\sin^4θ+⋯\right)\,dθ.\nonumber \]
a Kutumia tu muda wa kwanza katika integrand, makadirio ya kwanza ili ni
\[ T≈4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\,dθ=2π\sqrt{\dfrac{L}{g}}.\nonumber \]
Ikiwa\( θ_{max}\) ni ndogo, basi\( k=\sin\left(\dfrac{θ_{max}}{2}\right)\) ni ndogo. Tunadai kwamba wakati\( k\) ni ndogo, hii ni makadirio mazuri. Ili kuhalalisha madai haya, fikiria
\[ \int ^{π/2}_0\left(1+\frac{1}{2}k^2\sin^2θ+\dfrac{1⋅3}{2!2^2}k^4\sin^4θ+⋯\right)\,dθ.\nonumber \]
Tangu\( |\sin x|≤1\), muhimu hii imepakana na
\[ \int ^{π/2}_0\left(\dfrac{1}{2}k^2+\dfrac{1.3}{2!2^2}k^4+⋯\right)\,dθ\;<\;\dfrac{π}{2}\left(\dfrac{1}{2}k^2+\dfrac{1⋅3}{2!2^2}k^4+⋯\right).\nonumber \]
Zaidi ya hayo, inaweza kuonyeshwa kwamba kila mgawo upande wa kulia ni chini ya\( 1\) na, kwa hiyo, kwamba maneno haya yamepakana na
\( \dfrac{πk^2}{2}(1+k^2+k^4+⋯)=\dfrac{πk^2}{2}⋅\dfrac{1}{1−k^2}\),
ambayo ni ndogo kwa\( k\) wadogo.
b. maadili kubwa ya\( θ_{max}\), tunaweza takriban\( T\) kwa kutumia maneno zaidi katika integrand. Kwa kutumia maneno mawili ya kwanza katika muhimu, sisi kufika katika makadirio
\[ T≈4\sqrt{\frac{L}{g}}\int ^{π/2}_0\left(1+\dfrac{1}{2}k^2\sin^2θ\right)\,dθ=2π\sqrt{\dfrac{L}{g}}\left(1+\dfrac{k^2}{4}\right).\nonumber \]
Matumizi ya mfululizo wa Taylor katika sehemu hii ni nia ya kuonyesha umuhimu wao. Kwa ujumla, Taylor mfululizo ni muhimu kwa sababu wao kuruhusu sisi kuwakilisha kazi inayojulikana kwa kutumia polynomials, hivyo kutoa yetu chombo kwa ajili ya makadirio ya maadili kazi na kukadiria integrals ngumu. Kwa kuongeza, wanatuwezesha kufafanua kazi mpya kama mfululizo wa nguvu, hivyo kutupa chombo chenye nguvu cha kutatua equations tofauti.
Dhana muhimu
- Mfululizo wa binomial ni mfululizo wa Maclaurin kwa\( f(x)=(1+x)^r\). Ni hujiunga kwa\( |x|<1\).
- Taylor mfululizo kwa ajili ya kazi mara nyingi inaweza inayotokana na shughuli algebraic na inayojulikana Taylor mfululizo au kwa kutofautisha au kuunganisha inayojulikana Taylor mfululizo.
- Mfululizo wa nguvu unaweza kutumika kutatua usawa tofauti.
- Mfululizo wa Taylor unaweza kutumika kusaidia integrals takriban ambayo haiwezi kupimwa kwa njia nyingine.
faharasa
- mfululizo wa binomial
- mfululizo wa Maclaurin kwa\( f(x)=(1+x)^r\); hutolewa na\(\displaystyle (1+x)^r=\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+\dfrac{r(r−1)⋯(r−n+1)}{n!}x^n+⋯\) kwa\( |x|<1\)
- yasiyo ya msingi muhimu
- muhimu ambayo antiderivative ya integrand haiwezi kuelezwa kama kazi ya msingi


