9.4: Vipimo vya kulinganisha

Malengo ya kujifunza

• Tumia mtihani wa kulinganisha ili kupima mfululizo wa kuunganisha.
• Tumia mtihani wa kulinganisha kikomo ili kuamua muunganiko wa mfululizo.

Tumeona kwamba mtihani muhimu inaruhusu sisi kuamua muunganiko au tofauti ya mfululizo kwa kulinganisha na muhimu kuhusiana yasiyofaa. Katika sehemu hii, tunaonyesha jinsi ya kutumia vipimo vya kulinganisha ili kuamua muunganiko au tofauti ya mfululizo kwa kulinganisha na mfululizo ambao muunganiko au tofauti yake hujulikana. Kwa kawaida vipimo hivi hutumiwa kuamua muunganiko wa mfululizo ambao ni sawa na mfululizo wa kijiometri au\(p\) -mfululizo.

Mtihani wa kulinganisha

Katika sehemu mbili zilizopita, tulijadili madarasa mawili makubwa ya mfululizo: mfululizo wa kijiometri na\(p\) -mfululizo. Tunajua hasa wakati mfululizo huu hujiunga na wakati wanapotofautiana. Hapa tunaonyesha jinsi ya kutumia muunganiko au upatanisho wa mfululizo huu ili kuthibitisha muunganiko au tofauti kwa mfululizo mwingine, kwa kutumia njia inayoitwa mtihani wa kulinganisha.

Kwa mfano, fikiria mfululizo

\[\sum_{n=1}^∞\dfrac{1}{n^2+1}. \nonumber \]

Mfululizo huu unaonekana sawa na mfululizo unaobadilika

\[\sum_{n=1}^∞\dfrac{1}{n^2} \nonumber \]

Kwa kuwa maneno katika kila mfululizo ni chanya, mlolongo wa kiasi cha sehemu kwa kila mfululizo ni kuongezeka kwa monotone. Aidha, tangu

\[0<\dfrac{1}{n^2+1}<\dfrac{1}{n^2} \nonumber \]

kwa integers wote chanya\(n\), jumla ya\(k^{\text{th}}\) sehemu\(S_k\) ya\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2+1}\) satisfies

\[S_k=\sum_{n=1}^k\dfrac{1}{n^2+1}<\sum_{n=1}^k\dfrac{1}{n^2}<\sum_{n=1}^∞\dfrac{1}{n^2}. \nonumber \]

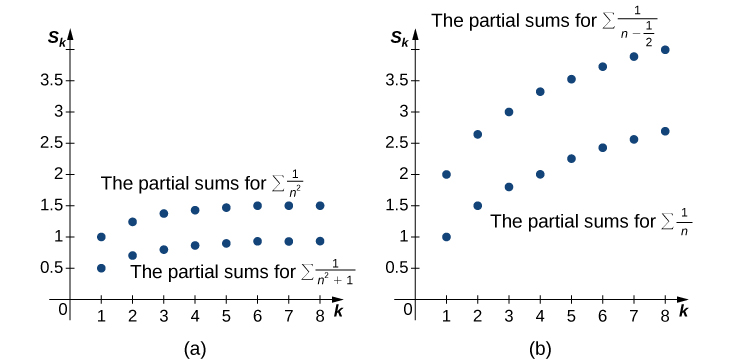
(Angalia Kielelezo\(\PageIndex{1a}\) na Jedwali\(\PageIndex{1}\).) Tangu mfululizo juu ya haki hujiunga, mlolongo\({S_k}\) umefungwa hapo juu. Tunahitimisha kwamba\({S_k}\) ni monotone kuongeza mlolongo kwamba ni imepakana juu. Kwa hiyo, kwa Theorem Monotone Convergence,\({S_k}\) converges, na hivyo

\[\sum_{n=1}^∞\dfrac{1}{n^2+1} \nonumber \]

hukutana.

Vile vile, fikiria mfululizo

\[\sum_{n=1}^∞\dfrac{1}{n−1/2}. \nonumber \]

Mfululizo huu unaonekana sawa na mfululizo tofauti

\[\sum_{n=1}^∞\dfrac{1}{n}. \nonumber \]

Mlolongo wa kiasi cha sehemu kwa kila mfululizo ni monotone kuongezeka na

\[\dfrac{1}{n−1/2}>\dfrac{1}{n}>0 \nonumber \]

kwa kila integer chanya\(n\). Kwa hiyo, jumla ya\(k^{\text{th}}\) sehemu\(S_k\) ya

\[ \sum^∞_{n=1}\dfrac{1}{n−1/2} \nonumber \]

hushibisha

\[S_k=\sum_{n=1}^k\dfrac{1}{n−1/2}>\sum_{n=1}^k\dfrac{1}{n}. \nonumber \]

(Angalia Kielelezo\(\PageIndex{1n}\) na Jedwali\(\PageIndex{1}\)). Kwa kuwa mfululizo\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) unajitokeza kwa infinity, mlolongo wa kiasi cha sehemu\(\displaystyle \sum^k_{n=1}\frac{1}{n}\) ni unbounded. Kwa hiyo,\({S_k}\) ni mlolongo unbounded, na kwa hiyo diverges. Tunahitimisha kwamba

\[\sum_{n=1}^∞\dfrac{1}{n−1/2} \nonumber \]

hutengana.

Kielelezo\(\PageIndex{1}\): (a) Kila moja ya kiasi cha sehemu ya mfululizo uliopewa ni chini ya sambamba sehemu ya jumla kwa converging\(p−series\). (b) Kila moja ya kiasi sehemu ya mfululizo kutokana ni kubwa kuliko sambamba sehemu jumla kwa diverging harmonic mfululizo.

Jedwali\(\PageIndex{1}\): Kulinganisha mfululizo na\(p\) -mfululizo (\(p = 2\))

\(k\)	1	2	3	4	5	6	7	8
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n^2+1}\)	0.5	0.7	0.8	0.8588	0.8973	0.9243	0.9443	0.9597
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n^2}\)	1	1.25	1.3611	1.4236	1.4636	1.4914	1.5118	1.5274

Jedwali\(\PageIndex{2}\): Kulinganisha mfululizo na mfululizo wa harmonic

\(k\)	1	2	3	4	5	6	7	8
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n−1/2}\)	2	2.6667	3.0667	3.3524	3.5746	3.7564	3.9103	4.0436
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n}\)	1	1.5	1.8333	2.0933	2.2833	2.45	2.5929	2.7179

Mtihani wa kulinganisha

1. Tuseme kuna integer\(N\) such that \(0≤a_n≤b_n\) for all \(n≥N\). If \(\displaystyle \sum^∞_{n=1}b_n\) converges, then \(\displaystyle \sum^∞_{n=1}a_n\) converges.
2. Tuseme kuna integer\(N\) such that \(a_n≥b_n≥0\) for all \(n≥N.\) If \(\displaystyle \sum^∞_{n=1}b_n\) diverges, then \(\displaystyle \sum^∞_{n=1}a_n\) diverges.

Ushahidi

Sisi kuthibitisha sehemu i. ushahidi wa sehemu ya ii. ni contrapositive ya sehemu i. basi\({S_k}\) be the sequence of partial sums associated with \(\displaystyle \sum^∞_{n=1}a_n\), and let \(\displaystyle L=\sum^∞_{n=1}b_n\). Since the terms \(a_n≥0,\)

\[S_k=a_1+a_2+⋯+a_k≤a_1+a_2+⋯+a_k+a_{k+1}=S_{k+1}. \nonumber \]

Kwa hiyo, mlolongo wa kiasi cha sehemu huongezeka. Zaidi ya hayo, tangu\(a_n≤b_n\) for all \(n≥N\), then

\[\sum_{n=N}^ka_n≤\sum_{n=N}^kb_n≤\sum_{n=1}^∞b_n=L. \nonumber \]

Kwa hiyo, kwa wote\(k≥1\),

\[S_k=(a_1+a_2+⋯+a_{N−1})+\sum_{n=N}^ka_n≤(a_1+a_2+⋯+a_{N−1})+L. \nonumber \]

Tangu\(a_1+a_2+⋯+a_{N−1}\) is a finite number, we conclude that the sequence \({S_k}\) is bounded above. Therefore, \({S_k}\) is an increasing sequence that is bounded above. By the Monotone Convergence Theorem, we conclude that \({S_k}\) converges, and therefore the series \(\displaystyle \sum_{n=1}^∞a_n\) converges.

□

Kutumia mtihani wa kulinganisha ili kuamua muunganiko au tofauti ya mfululizo\(\displaystyle \sum_{n=1}^∞a_n\), it is necessary to find a suitable series with which to compare it. Since we know the convergence properties of geometric series and \(p\)-series, these series are often used. If there exists an integer \(N\) such that for all \(n≥N\), each term an is less than each corresponding term of a known convergent series, then \(\displaystyle \sum_{n=1}^∞a_n\) converges. Similarly, if there exists an integer \(N\) such that for all \(n≥N\), each term an is greater than each corresponding term of a known divergent series, then \(\displaystyle \sum_{n=1}^∞a_n\) diverges.

Mfano\(\PageIndex{1}\): Using the Comparison Test

Kwa kila mfululizo wafuatayo, tumia mtihani wa kulinganisha ili uone kama mfululizo unajiunga au hupungua.

1. \(\displaystyle \sum_{n=1}^∞=\dfrac{1}{n^3+3n+1}\)
2. \(\displaystyle \sum_{n=1}^∞=\dfrac{1}{2^n+1}\)
3. \(\displaystyle \sum_{n=2}^∞=\dfrac{1}{\ln \,n }\)

Suluhisho

a. kulinganisha na\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\). Kwa kuwa\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\) ni\(p\) -mfululizo na\(p=3\), hujiunga. Zaidi ya hayo,

\[\dfrac{1}{n^3+3n+1}<\dfrac{1}{n^3} \nonumber \]

kwa kila integer chanya\(n\). Kwa hiyo, tunaweza kuhitimisha kwamba\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^3+3n+1}\) hujiunga.

b. kulinganisha na\(\displaystyle \sum^∞_{n=1}\left(\dfrac{1}{2}\right)^n\). Kwa kuwa\(\displaystyle \sum_{n=1}^∞\left(\dfrac{1}{2}\right)^n\) ni mfululizo wa kijiometri\(r=\dfrac{1}{2}\) na na\(\left|\dfrac{1}{2}\right|<1\), hujiunga. Pia,

\[\dfrac{1}{2^n+1}<\dfrac{1}{2^n} \nonumber \]

kwa kila integer chanya\(n\). Kwa hiyo, tunaona kwamba\(\displaystyle \sum^∞_{n=1}\dfrac{1}{2^n+1}\) hujiunga.

c. kulinganisha na\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n}\). Tangu

\[\dfrac{1}{\ln n }>\dfrac{1}{n} \nonumber \]

kwa kila integer\(n≥2\) na\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n}\) diverges, tuna kwamba\(\displaystyle \sum^∞_{n=2}\dfrac{1}{\ln n}\) diverges.

Zoezi\(\PageIndex{1}\)

Tumia mtihani wa kulinganisha ili uone ikiwa mfululizo\(\displaystyle \sum^∞_{n=1}\dfrac{n}{n^3+n+1}\) unajiunga au unapungua.

Kidokezo

Pata thamani\(p\) kama hiyo\(\dfrac{n}{n^3+n+1}≤\dfrac{1}{n^p}\).

Jibu

Mfululizo hujiunga.

Limit kulinganisha mtihani

mtihani kulinganisha kazi vizuri kama tunaweza kupata mfululizo kulinganishwa kuridhisha hypothesis ya mtihani. Hata hivyo, wakati mwingine kutafuta mfululizo sahihi inaweza kuwa vigumu. Fikiria mfululizo

\[\sum_{n=2}^∞\dfrac{1}{n^2−1}. \nonumber \]

Ni kawaida kulinganisha mfululizo huu na mfululizo unaobadilika.

\[\sum_{n=2}^∞\dfrac{1}{n^2}. \nonumber \]

Hata hivyo, mfululizo huu haikidhi hypothesis muhimu kutumia mtihani wa kulinganisha kwa sababu

\[\dfrac{1}{n^2−1}>\dfrac{1}{n^2} \nonumber \]

kwa integers wote\(n≥2\). Ingawa tunaweza kuangalia kwa mfululizo tofauti na ambayo kulinganisha\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2−1},\) badala sisi kuonyesha jinsi tunaweza kutumia kikomo kulinganisha mtihani kulinganisha

\[\sum_{n=2}^∞\frac{1}{n^2−1} \nonumber \]

na

\[\sum_{n=2}^∞\frac{1}{n^2}. \nonumber \]

Hebu tuchunguze wazo nyuma ya mtihani wa kulinganisha kikomo. Fikiria mbili mfululizo\(\displaystyle \sum^∞_{n=1}a_n\)\(\displaystyle \sum^∞_{n=1}b_n\) na. kwa maneno mazuri\(a_n\)\(b_n\) na kutathmini

\[\lim_{n→∞}\frac{a_n}{b_n}. \nonumber \]

Kama

\[\lim_{n→∞}\frac{a_n}{b_n}=L≠0, \nonumber \]

basi, kwa\(n\) kutosha kubwa,\(a_n≈Lb_n\). Kwa hiyo, ama mfululizo wote hujiunga au mfululizo wote hutofautiana. Kwa mfululizo\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2−1}\) na\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n^2}\), tunaona kwamba

\[\lim_{n→∞}\dfrac{1/(n^2−1)}{1/n^2}=\lim_{n→∞}\dfrac{n^2}{n^2−1}=1. \nonumber \]

Tangu\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2}\) converges, sisi kuhitimisha kwamba

\[\sum_{n=2}^∞\dfrac{1}{n^2−1} \nonumber \]

hukutana.

Mtihani wa kulinganisha kikomo unaweza kutumika katika kesi nyingine mbili. Tuseme

\[\lim_{n→∞}\dfrac{a_n}{b_n}=0. \nonumber \]

Katika kesi hii,\({a_n/b_n}\) ni mlolongo imepakana. Matokeo yake, kuna mara kwa mara\(M\) kama hiyo\(a_n≤Mb_n\). Kwa hiyo, ikiwa\(\displaystyle \sum^∞_{n=1}b_n\) hujiunga, kisha\(\displaystyle \sum^∞_{n=1}a_n\) hujiunga. Kwa upande mwingine, tuseme

\[\lim_{n→∞}\dfrac{a_n}{b_n}=∞. \nonumber \]

Katika kesi hii,\({a_n/b_n}\) ni mlolongo unbounded. Kwa hiyo, kwa kila mara\(M\) kuna integer\(N\) kama hiyo\(a_n≥Mb_n\) kwa wote\(n≥N.\) Kwa hiyo,\(\displaystyle \sum^∞_{n=1}b_n\) ikiwa hupungua,\(\displaystyle \sum^∞_{n=1}a_n\) kisha hupungua pia.

Limit kulinganisha mtihani

Hebu\(a_n,b_n≥0\) kwa wote\(n≥1.\)

1. Ikiwa\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=L≠0,\) basi\(\displaystyle \sum^∞_{n=1}a_n\) na\(\displaystyle \sum^∞_{n=1}b_n\) wote wawili hujiunga au wote wawili wanatofautiana.
2. Ikiwa\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=0\) na\(\displaystyle \sum^∞_{n=1}b_n\) hujiunga, kisha\(\displaystyle \sum^∞_{n=1}a_n\) hujiunga.
3. Ikiwa\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=∞\) na\(\displaystyle \sum^∞_{n=1}b_n\) hutofautiana, basi\(\displaystyle \sum^∞_{n=1}a_n\) hupungua.

Kumbuka kwamba ikiwa\(\dfrac{a_n}{b_n}→0\) na\(\displaystyle \sum^∞_{n=1}b_n\) hutofautiana, mtihani wa kulinganisha kikomo hautoi habari. Vile vile, ikiwa\(\dfrac{a_n}{b_n}→∞\) na\(\displaystyle \sum^∞_{n=1}b_n\) hujiunga, mtihani pia hautoi habari. Kwa mfano, fikiria mfululizo mbili\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}\) na\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\). Mfululizo huu ni wote\(p\) -mfululizo\(p=\frac{1}{2}\) na\(p=2\), kwa mtiririko huo. Tangu\(p=\frac{1}{2}<1,\) mfululizo\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}\) hupungua. Kwa upande mwingine, tangu\(p=2>1\), mfululizo\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) hujiunga. Hata hivyo, tuseme tulijaribu kutumia mtihani wa kulinganisha kikomo, kwa kutumia \(p\)mfululizo wa mfululizo\(\displaystyle \sum_{n=1}^∞\frac{1}{n^3}\) kama mfululizo wetu wa kulinganisha. Kwanza, tunaona kwamba

\[\dfrac{1/\sqrt{n}}{1/n^3}=\dfrac{n^3}{\sqrt{n}}=n^{5/2}→∞\; \text{ as } \;n→∞. \nonumber \]

Vile vile, tunaona kwamba

\[\dfrac{1/n^2}{1/n^3}=n→∞\; \text{ as } \;n→∞. \nonumber \]

Kwa hiyo, kama\(\dfrac{a_n}{b_n}→∞\) wakati\(\displaystyle \sum_{n=1}^∞b_n\) converges, hatuwezi kupata taarifa yoyote juu ya muunganiko au tofauti ya\(\displaystyle \sum_{n=1}^∞a_n\).

Mfano\(\PageIndex{2}\): Using the Limit Comparison Test

Kwa kila moja ya mfululizo wafuatayo, tumia mtihani wa kulinganisha kikomo ili uone kama mfululizo unajiunga au hupungua. Ikiwa mtihani hautumiki, sema hivyo.

1. \(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}+1}\)
2. \(\displaystyle \sum^∞_{n=1}\dfrac{2^n+1}{3^n}\)
3. \(\displaystyle \sum^∞_{n=1}\dfrac{\ln(n)}{n^2}\)

Suluhisho

a. kulinganisha mfululizo huu kwa\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}}\). Tumia

\(\displaystyle \lim_{n→∞}\dfrac{1/(\sqrt{n}+1)}{1/\sqrt{n}}=\lim_{n→∞}\dfrac{\sqrt{n}}{\sqrt{n}+1}=\lim_{n→∞}\dfrac{1/\sqrt{n}}{1+1/\sqrt{n}}=1.\)

Kwa mtihani wa kulinganisha kikomo,\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}}\) tangu hupungua, kisha\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}+1}\) hupungua.

b. kulinganisha mfululizo huu kwa\(\displaystyle \sum^∞_{n=1}\left(\dfrac{2}{3}\right)^n\). Tunaona kwamba

\(\displaystyle \lim_{n→∞}\dfrac{(2^n+1)/3^n}{2^n/3^n}=\lim_{n→∞}\dfrac{2^n+1}{3^n}⋅\dfrac{3^n}{2^n}=\lim_{n→∞}\dfrac{2^n+1}{2^n}=\lim_{n→∞}\left[1+\left(\tfrac{1}{2}\right)^n\right]=1.\)

Kwa hiyo,

\(\displaystyle \lim_{n→∞}\dfrac{(2^n+1)/3^n}{2^n/3^n}=1.\)

Tangu\(\displaystyle \sum^∞_{n=1}\left(\dfrac{2}{3}\right)^n\) hujiunga, tunahitimisha kuwa\(\displaystyle \sum^∞_{n=1}\dfrac{2^n+1}{3^n}\) hujiunga.

c. tangu\(\ln n<n,\) kulinganisha na\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n}\). Tunaona kwamba

\(\displaystyle \lim_{n→∞}\dfrac{\ln n/n^2}{1/n}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n}{1}=\lim_{n→∞}\dfrac{\ln n}{n}.\)

Ili kutathmini\(\displaystyle \lim_{n→∞}\ln n/n\), tathmini kikomo kama\(x→∞\) ya kazi halisi ya thamani\(\ln(x)/x\). Mipaka hii miwili ni sawa, na kufanya mabadiliko haya inatuwezesha kutumia utawala wa L'Hôpital. Tunapata

\(\displaystyle \lim_{x→∞}\dfrac{lnx}{x}=\lim_{x→∞}\dfrac{1}{x}=0.\)

Kwa hiyo\(\displaystyle \lim_{n→∞}\frac{\ln n}{n}=0\), na, kwa hiyo,

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n}=0.\)

Kwa kuwa kikomo ni\(0\) lakini\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n}\) kinapungua, mtihani wa kulinganisha kikomo haitoi taarifa yoyote.

Linganisha na\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2}\) badala yake. Katika kesi hiyo,

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n^2}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n^2}{1}=\lim_{n→∞}\ln n=∞.\)

Kwa kuwa kikomo ni\(∞\) lakini\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2}\) hujiunga, mtihani bado hautoi taarifa yoyote.

Kwa hiyo sasa tunajaribu mfululizo kati ya mbili ambazo tayari tumejaribu. Kuchagua mfululizo\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{3/2}}\), tunaona kwamba

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n^{3/2}}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n^{3/2}}{1}=\lim_{n→∞}\dfrac{\ln n}{\sqrt{n}}\).

Kama hapo juu, ili kutathmini\(\displaystyle \lim_{n→∞}\frac{\ln n}{\sqrt{n}}\), tathmini kikomo kama\(x→∞\) ya kazi halisi ya thamani\(\frac{\ln n}{\sqrt{n}}\). Kwa kutumia utawala wa L'Hôpital,

\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{\sqrt{x}}=\lim_{x→∞}\dfrac{2\sqrt{x}}{x}=\lim_{x→∞}\dfrac{2}{\sqrt{x}}=0\).

Kwa kuwa kikomo ni\(0\) na\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{3/2}}\) hujiunga, tunaweza kuhitimisha kwamba\(\displaystyle \sum^∞_{n=1}\dfrac{\ln n}{n^2}\) hujiunga.

Zoezi\(\PageIndex{2}\)

Tumia mtihani wa kulinganisha kikomo ili uone kama mfululizo\(\displaystyle \sum^∞_{n=1}\dfrac{5^n}{3^n+2}\) unajiunga au hupungua.

Kidokezo

Linganisha na mfululizo wa kijiometri.

Jibu

Mfululizo hutofautiana.

Dhana muhimu

• Vipimo vya kulinganisha hutumiwa kuamua kuunganishwa au kutofautiana kwa mfululizo na maneno mazuri.
• Wakati wa kutumia vipimo vya kulinganisha, mfululizo mara nyingi\(\displaystyle \sum^∞_{n=1}a_n\) hulinganishwa na kijiometri au\(p\) -mfululizo.

faharasa

mtihani wa kulinganisha

Ikiwa\(0≤a_n≤b_n\) kwa wote\(n≥N\) na\(\displaystyle \sum^∞_{n=1}b_n\) hujiunga, basi\(\displaystyle \sum^∞_{n=1}a_n\) hujiunga; ikiwa\(a_n≥b_n≥0\) kwa wote\(n≥N\)\(\displaystyle \sum^∞_{n=1}b_n\) na hupungua, basi\(\displaystyle \sum^∞_{n=1}a_n\) hupungua.

mtihani wa kulinganisha kikomo

Tuseme\(a_n,b_n≥0\) kwa wote\(n≥1\). Ikiwa\(\displaystyle \lim_{n→∞}a_n/b_n→L≠0\), basi\(\displaystyle \sum^∞_{n=1}a_n\) na\(\displaystyle \sum^∞_{n=1}b_n\) wote wawili hujiunga au wote wawili wanatofautiana; ikiwa\(\displaystyle \lim_{n→∞}a_n/b_n→0\) na\(\displaystyle \sum^∞_{n=1}b_n\) hujiunga, kisha\(\displaystyle \sum^∞_{n=1}a_n\) hujiunga. Ikiwa\(\displaystyle \lim_{n→∞}a_n/b_n→∞\), na\(\displaystyle \sum^∞_{n=1}b_n\) hupungua, basi\(\displaystyle \sum^∞_{n=1}a_n\) hupungua.