7.3: Badala ya Trigonometric

Last updated
Save as PDF

Page ID: 178841

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Kutatua matatizo ya ushirikiano kuwashirikisha mizizi mraba wa jumla au tofauti ya mraba mbili.

Katika sehemu hii, sisi kuchunguza integrals zenye maneno ya fomu\(\sqrt{a^2−x^2}\),\(\sqrt{a^2+x^2}\), na\(\sqrt{x^2−a^2}\), ambapo maadili ya\(a\) ni chanya. Tayari tumekutana na tathmini integrals zenye baadhi ya maneno ya aina hii, lakini wengi bado hawapatikani. Mbinu ya kubadilisha trigonometric inakuja kwa manufaa sana wakati wa kutathmini vipengele hivi. Mbinu hii inatumia badala ya kuandika upya integrals hizi kama integrals trigonometric.

Integrals Kushirikisha\(\sqrt{a^2−x^2}\)

Kabla ya kuendeleza mkakati wa jumla kwa integrals zenye\(\sqrt{a^2−x^2}\), fikiria muhimu muhimu\(\displaystyle ∫\textstyle\sqrt{9−x^2}dx.\) Hii haiwezi tathmini kwa kutumia yoyote ya mbinu tumejadiliwa hadi sasa. Hata hivyo, kama sisi kufanya badala\(x=3\sin θ\), tuna\(dx=3\cos θ \, dθ.\) Baada ya kubadilisha katika muhimu, tuna

\[ ∫\sqrt{9−x^2}\,dx=∫\textstyle\sqrt{ 9−(3\sin θ)^2}\cdot 3\cos θ \,dθ. \nonumber \]

Baada ya kurahisisha, tuna

\[ ∫\sqrt{ 9−x^2}\,dx=∫ 9\textstyle\sqrt{1−\sin^2θ}\cdot\cos θ \, dθ. \nonumber \]

Kuruhusu\(1−\sin^2θ=\cos^2θ,\) sisi sasa

\[ ∫\sqrt{ 9−x^2}\,dx=∫ 9\textstyle\sqrt{\cos^2θ}\cos θ \, dθ. \nonumber \]

Kutokana kwamba\(\cos θ≥0\), tuna

\[ ∫\textstyle\sqrt{ 9−x^2}\,dx=∫ 9\cos^2θ \, dθ. \nonumber \]

Kwa hatua hii, tunaweza kutathmini muhimu kwa kutumia mbinu zilizotengenezwa kwa kuunganisha nguvu na bidhaa za kazi za trigonometric. Kabla ya kukamilisha mfano huu, hebu tuangalie nadharia ya jumla nyuma ya wazo hili.

Kutathmini integrals kuwashirikisha\(\sqrt{a^2−x^2}\), sisi kufanya badala\(x=a\sin θ\) na\(dx=a\cos θ\). Kuona kwamba hii kweli mantiki, fikiria hoja zifuatazo: uwanja wa\(\sqrt{a^2−x^2}\) ni\([−a,a]\). Hivyo,

\[−a≤x≤a. \nonumber \]

Kwa hiyo,

\[−1≤\dfrac{x}{a}≤1. \nonumber \]

Kwa kuwa mbalimbali ya\(\sin x\) juu\([−(π/2),π/2]\) ni\([−1,1]\), kuna angle ya kipekee\(θ\) kuridhisha\(−(π/2)≤θ≤π/2\) ili\(\sin θ=x/a\), au equivalently, ili\(x=a\sin θ\). Kama sisi badala\(x=a\sin θ\) katika\(\sqrt{a^2−x^2}\), sisi kupata

\\ kuanza {kuungana*}\ sqrt {a^2,1x^2} &=\ sqrt {a ^ 2 - (a\ dhambi η) ^2} &\ maandishi {Hebu} x=a\ dhambi η\ maandishi {wapi}}} {2} {2} {2}.\\ [4pt] & & &\ maandishi {2} {2}.\\ [4pt]
& & &\ maandishi {2} Kurahisisha.}\\ [4pt]
&=\ sqrt {a ^ 2,1a ^ 2\ sin^2} & &\ maandishi {Factor nje} a ^ 2.\\ [4pt]
&=\ sqrt {a ^ 2 (1-\ dhambi ^2)} & &\ maandishi {mbadala} 1-\ dhambi ^ 2x=\ cos ^ 2x.\\ [4pt]
&=\ sqrt {a ^ 2\ cos ^2} & &\ maandishi {Chukua mizizi
ya mraba.}\\ [4pt]
&=\ [cos η\ mwisho {align*}\]

Tangu\(\cos x≥0\) juu\(−\dfrac{π}{2}≤θ≤\dfrac{π}{2}\) na\(a>0, |a\cos θ|=a\cos θ.\) Tunaweza kuona, kutokana na mjadala huu, kwamba kwa kufanya badala\(x=a\sin θ\), tuna uwezo wa kubadili muhimu kuwashirikisha radical katika muhimu kuwashirikisha kazi trigonometric. Baada ya kutathmini muhimu, tunaweza kubadilisha ufumbuzi nyuma kujieleza kuwashirikisha\(x\). Kuona jinsi ya kufanya hivyo, hebu tuanze kwa kudhani hilo\(0<x<a\). Katika kesi hii,\(0<θ<\dfrac{π}{2}\). Tangu\(\sin θ=\dfrac{x}{a}\), tunaweza kuteka pembetatu kumbukumbu katika Kielelezo\(\PageIndex{1}\) kusaidia katika kuonyesha maadili ya\(\cos θ, \, \tan θ,\) na iliyobaki kazi trigonometric katika suala la x Inaweza kuonyeshwa kuwa pembetatu hii kweli inazalisha maadili sahihi ya kazi trigonometric tathmini katika\(θ\) kwa ajili ya wote\(θ\) kuridhisha\(−\dfrac{π}{2}≤θ≤\dfrac{π}{2}\). Ni muhimu kuchunguza kwamba maneno yanaonekana\(\sqrt{a^2−x^2}\) kama urefu wa upande mmoja wa pembetatu. Mwisho, inapaswa\(θ\) kuonekana yenyewe, tunatumia\(θ=\sin^{−1}\left(\dfrac{x}{a}\right).\)

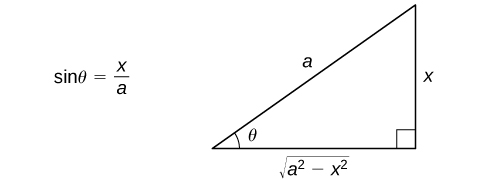
Takwimu hii ni pembetatu sahihi. Ina angle kinachoitwa theta. Pembe hii ni kinyume na upande wa wima. Hypotenuse ni kinachoitwa, mguu wima ni lebo x, na mguu usawa ni kinachoitwa kama mizizi mraba ya (a ^ 2 - x ^ 2). Upande wa kushoto wa pembetatu ni dhambi ya equation (theta) = x/a. — Kielelezo\(\PageIndex{1}\): pembetatu rejea inaweza kusaidia kueleza kazi trigonometric tathmini\(θ\) katika suala la\(x\).

Sehemu muhimu ya mjadala huu ni muhtasari katika mkakati wafuatayo wa kutatua matatizo.

Mkakati wa Kutatua matatizo: Kuunganisha Maneno Kuhusisha\(\sqrt{a^2−x^2}\)

Ni wazo nzuri kuhakikisha muhimu haiwezi kupimwa kwa urahisi kwa njia nyingine. Kwa mfano, ingawa njia hii inaweza kutumika kwa integrals ya fomu\(\displaystyle ∫\dfrac{1}{\sqrt{a^2−x^2}}dx\),\(\displaystyle ∫\dfrac{x}{\sqrt{a^2−x^2}}dx,\) na\(\displaystyle ∫x\sqrt{a^2−x^2}\,dx,\) wanaweza kila mmoja kuunganishwa moja kwa moja ama kwa formula au kwa rahisi\(u\) -badala.
Kufanya badala\(x=a \sin θ\) na\(dx=a\cos θ \,dθ.\) Kumbuka: Hii mavuno badala\(\sqrt{a^2−x^2}=a\cos θ.\)
Kurahisisha usemi.
Tathmini mbinu muhimu za kutumia kutoka sehemu ya integrals trigonometric.
Tumia pembetatu ya kumbukumbu kutoka Kielelezo 1 ili uandike upya matokeo kwa suala la\(x\). Unaweza pia haja ya kutumia baadhi ya utambulisho trigonometric na uhusiano\(θ=\sin^{−1}\left(\dfrac{x}{a}\right).\)

Mfano unaofuata unaonyesha matumizi ya mkakati huu wa kutatua matatizo.

Mfano\(\PageIndex{1}\): Integrating an Expression Involving \(\sqrt{a^2−x^2}\)

Tathmini

\[ ∫\sqrt{ 9−x^2}dx. \nonumber \]

Suluhisho

Kuanza kwa kufanya mbadala\(x=3\sin θ\) na\(dx=3\cos θ \, dθ.\) Tangu\(\sin θ=\dfrac{x}{3}\), tunaweza kujenga pembetatu kumbukumbu inavyoonekana katika Kielelezo 2.

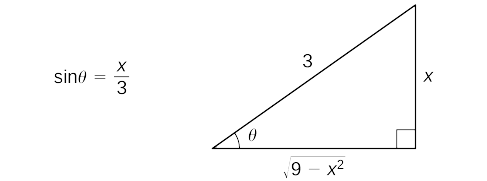
Takwimu hii ni pembetatu sahihi. Ina angle kinachoitwa theta. Pembe hii ni kinyume na upande wa wima. Hypotenuse inaitwa 3, mguu wa wima umeandikwa x, na mguu usio na usawa umeandikwa kama mizizi ya mraba ya (9 - x ^ 2). Upande wa kushoto wa pembetatu ni dhambi ya equation (theta) = x/3. — Kielelezo\(\PageIndex{2}\): pembetatu ya kumbukumbu inaweza kujengwa kwa Mfano\(\PageIndex{1}\).

Hivyo,

\[ ∫\sqrt{9−x^2}\,dx=∫\sqrt{ 9−(3\sin θ)^2}3\cos θ\,dθ \nonumber \]

Mbadala\(x=3\sin θ\) na\(dx=3\cos θ \,dθ\).

\(=∫\sqrt{ 9(1−\sin^2θ)}\cdot 3\cos θ \, dθ\)Kurahisisha.

\(=∫\sqrt{ 9\cos^2θ}\cdot 3\cos θ \, dθ\)Mbadala\(\cos^2θ=1−\sin^2θ\).

\(=∫ 3|\cos θ|3\cos θ \, dθ\)Chukua mizizi ya mraba.

\(=∫ 9\cos^2θ \, dθ\)Kurahisisha. Tangu\(−\dfrac{π}{2}≤θ≤\dfrac{π}{2},\cos θ≥0\) na\(|\cos θ|=\cos θ.\)

\(=∫ 9\left(\dfrac{1}{2}+\dfrac{1}{2}\cos(2θ)\right)\,dθ\)Kutumia mkakati wa kuunganisha hata nguvu ya\(\cos θ\).

\(=\dfrac{9}{2}θ+\dfrac{9}{4}\sin(2θ)+C\)Tathmini muhimu.

\(=\dfrac{9}{2}θ+\dfrac{9}{4}(2\sin θ\cos θ)+C\)

Mbadala\(\sin(2θ)=2\sin θ\cos θ\).

\(=\dfrac{9}{2}\sin^{−1}\left(\dfrac{x}{3}\right)+\dfrac{9}{2}⋅\dfrac{x}{3}⋅\dfrac{\sqrt{9−x^2}}{3}+C\)Mbadala\(\sin^{−1}\left(\dfrac{x}{3}\right)=θ\) na\(\sin θ=\frac{x}{3}\). Tumia pembetatu ya kumbukumbu ili uone hilo\(\cos θ=\dfrac{\sqrt{9−x^2}}{3} \) na ufanye nafasi hii. Kurahisisha.

\(=\dfrac{9}{2}\sin^{−1}\left(\dfrac{x}{3}\right)+\dfrac{x\sqrt{9−x^2}}{2}+C.\)Kurahisisha.

Mfano\(\PageIndex{2}\): Integrating an Expression Involving \(\sqrt{a^2−x^2}\)

Tathmini

\[ ∫\dfrac{\sqrt{4−x^2}}{x}dx. \nonumber \]

Suluhisho

Kwanza fanya mbadala\(x=2\sin θ\) na\(dx=2\cos θ\,dθ\). Tangu\(\sin θ=\dfrac{x}{2}\), tunaweza kujenga pembetatu kumbukumbu inavyoonekana katika Kielelezo\(\PageIndex{3}\).

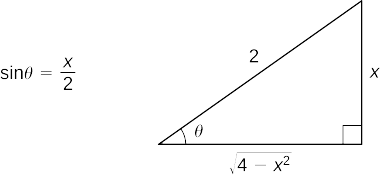
Takwimu hii ni pembetatu sahihi. Ina angle kinachoitwa theta. Pembe hii ni kinyume na upande wa wima. Mguu wa wima umeandikwa x, na mguu usio na usawa umeandikwa kama mizizi ya mraba ya (4 — x ^ 2). Upande wa kushoto wa pembetatu ni dhambi ya equation (theta) = x/2. — Kielelezo\(\PageIndex{3}\): pembetatu ya kumbukumbu inaweza kujengwa kwa Mfano\(\PageIndex{2}\).

Hivyo,

\(∫\dfrac{\sqrt{4−x^2}}{x}dx=∫\dfrac{\sqrt{4−(2\sin θ)^2}}{2\sin θ}2\cos θ \, dθ\)Mbadala\(x=2\sin θ\) na\(dx=2\cos θ\,dθ.\)

\(=∫\dfrac{2\cos^2θ}{\sin θ}\,dθ\)Mbadala\(\cos^2θ=1−\sin^2θ\) na kurahisisha.

\(=∫\dfrac{2(1−\sin^2θ)}{\sin θ}\,dθ\)Mbadala\(\cos^2θ=1−\sin^2θ\).

\(=∫ (2\csc θ−2\sin θ)\,dθ\)Toa namba, kurahisisha, na utumie\(\csc θ=\dfrac{1}{\sin θ}\).

\(=2 \ln |\csc θ−\cot θ|+2\cos θ+C\)Tathmini muhimu.

\(=2 \ln \left|\dfrac{2}{x}−\dfrac{\sqrt{4−x^2}}{x}\right|+\sqrt{4−x^2}+C.\)Tumia pembetatu ya kumbukumbu ili uandike upya maneno kwa suala la\(x\) na kurahisisha.

Katika mfano unaofuata, tunaona kwamba wakati mwingine tuna uchaguzi wa mbinu.

Mfano\(\PageIndex{3}\): Integrating an Expression Involving \(\sqrt{a^2−x^2}\) Two Ways

Tathmini njia\(∫ x^3\sqrt{1−x^2}dx\) mbili: kwanza kwa kutumia mbadala\(u=1−x^2\) na kisha kwa kutumia badala ya trigonometric.

Njia ya 1

Hebu\(u=1−x^2\) na hivyo\(x^2=1−u\). Hivyo,\(du=−2x\,dx.\) Katika kesi hiyo, muhimu inakuwa

\(∫ x^3\sqrt{1−x^2}\,dx=−\dfrac{1}{2}∫ x^2\sqrt{1−x^2}(−2x\,dx)\)Fanya badala.

\(=−\dfrac{1}{2}∫ (1−u)\sqrt{u}\,du\)Panua maneno.

\(=−\dfrac{1}{2}∫(u^{1/2}−u^{3/2})\,du\)Tathmini muhimu.

\(=−\dfrac{1}{2}(\dfrac{2}{3}u^{3/2}−\dfrac{2}{5}u^{5/2})+C\)Andika upya kwa suala la x.

\(=−\dfrac{1}{3}(1−x^2)^{3/2}+\dfrac{1}{5}(1−x^2)^{5/2}+C.\)

Njia ya 2

Hebu\(x=\sin θ\). Katika hali hii,\(dx=\cos θ \, dθ.\) Kutumia badala hii, tuna

\(∫ x^3\sqrt{1−x^2}dx=∫ \sin^3θ\cos^2θ \, dθ\)

\(=∫ (1−\cos^2θ)\cos^2θ\sin θ \, dθ\)\(u=\cos θ\)heka.Hivyo,\(du=−\sin θ \, dθ.\)

\(=∫ (u^4−u^2)\,du\)

\(=\dfrac{1}{5}u^5−\dfrac{1}{3}u^3+C\)Mbadala\(\cos θ=u.\)

\(=\dfrac{1}{5}\cos^5θ−\dfrac{1}{3}\cos^3θ+C\)Tumia pembetatu ya kumbukumbu ili uone\(\cos θ=\sqrt{1−x^2}.\)

\(=\dfrac{1}{5}(1−x^2)^{5/2}−\dfrac{1}{3}(1−x^2)^{3/2}+C.\)

Zoezi\(\PageIndex{1}\)

Andika upya muhimu\(\displaystyle ∫\dfrac{x^3}{\sqrt{25−x^2}}\,dx\) kwa kutumia mbadala sahihi ya trigonometric (usitathmini muhimu).

Kidokezo: Mbadala\(x=5\sin θ\) na\(dx=5\cos θ \, dθ.\)

Jibu: \(\displaystyle ∫ 125\sin^3θ \, dθ\)

Kuunganisha Maneno Kuhusisha\(\sqrt{a^2+x^2}\)

Kwa integrals zenye\(\sqrt{a^2+x^2}\), hebu kwanza fikiria uwanja wa maneno haya. Tangu\(\sqrt{a^2+x^2}\) hufafanuliwa kwa maadili yote halisi ya\(x\), sisi kuzuia uchaguzi wetu kwa wale kazi trigonometric ambayo mbalimbali ya idadi yote halisi. Hivyo, uchaguzi wetu ni vikwazo kwa kuchagua ama\(x=a\tan θ\) au\(x=a\cot θ\). Aidha ya mbadala hizi ingekuwa kweli kazi, lakini badala ya kiwango ni\(x=a\tan θ\) au, equivalently,\(\tan θ=x/a\). Na badala hii, sisi kufanya dhana kwamba\(−(π/2)<θ<π/2\), ili sisi pia kuwa na utaratibu\(θ=\tan^{−1}(x/a).\) wa kutumia badala hii ni ilivyoainishwa katika zifuatazo kutatua matatizo mkakati.

Mkakati wa Kutatua matatizo: Kuunganisha Maneno Kuhusisha\(\sqrt{a^2+x^2}\)

Angalia ili uone kama muhimu inaweza kupimwa kwa urahisi kwa kutumia njia nyingine. Katika hali nyingine, ni rahisi zaidi kutumia njia mbadala.
Mbadala\(x=a\tan θ\) na\(dx=a\sec^2θ \, dθ.\) Hii mazao badala\(\sqrt{a^2+x^2}=\sqrt{a^2+(a\tan θ)^2}=\sqrt{a^2(1+\tan^2θ)}=\sqrt{a^2sec^2θ}=|a\sec θ|=a\sec θ.\) (Tangu\(−\dfrac{π}{2}<θ<\dfrac{π}{2}\) na\(\sec θ>0\) zaidi ya kipindi hiki,\(|a\sec θ|=a\sec θ\).)
Kurahisisha usemi.
Tathmini mbinu muhimu za kutumia kutoka sehemu ya integrals trigonometric.
Tumia pembetatu ya kumbukumbu kutoka Kielelezo\(\PageIndex{4}\) ili uandike upya matokeo katika suala la\(x\). Unaweza pia haja ya kutumia baadhi ya utambulisho trigonometric na uhusiano\(θ=\tan^{−1}\left(\dfrac{x}{a}\right)\). (Kumbuka: Pembetatu ya kumbukumbu inategemea dhana kwamba\(x>0\); hata hivyo, uwiano wa trigonometric zinazozalishwa kutoka pembetatu ya kumbukumbu ni sawa na uwiano ambao\(x≤0\).)

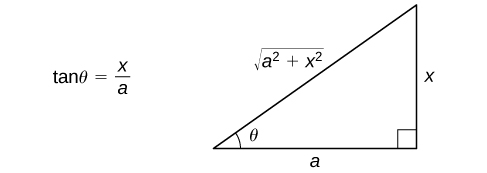
Takwimu hii ni pembetatu sahihi. Ina angle kinachoitwa theta. Pembe hii ni kinyume na upande wa wima. Hypotenuse ni kinachoitwa mizizi mraba ya (a ^ 2+x ^ 2), mguu wima ni kinachoitwa x, na mguu usawa ni kinachoitwa a. — Kielelezo\(\PageIndex{4}\): pembetatu ya kumbukumbu inaweza kujengwa ili kuelezea kazi za trigonometric zilizopimwa\(θ\) kwa suala la\(x\).

Mfano\(\PageIndex{4}\): Integrating an Expression Involving \(\sqrt{a^2+x^2}\)

Tathmini\(\displaystyle ∫\dfrac{dx}{\sqrt{1+x^2}}\) na uangalie suluhisho kwa kutofautisha.

Suluhisho

Anza na ubadilishaji\(x=\tan θ\) na\(dx=sec^2θ\,dθ\). Tangu\(\tan θ=x\), futa pembetatu ya kumbukumbu katika Kielelezo\(\PageIndex{5}\).

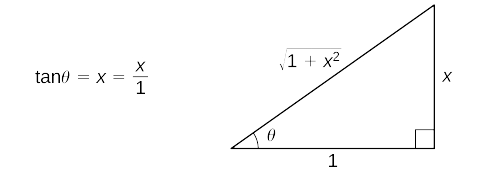
Takwimu hii ni pembetatu sahihi. Ina angle kinachoitwa theta. Pembe hii ni kinyume na upande wa wima. Hypotenuse inaitwa mizizi ya mraba ya (1+x ^ 2), mguu wa wima umeandikwa x, na mguu usio na usawa umeandikwa 1. Upande wa kushoto wa pembetatu ni tan ya equation (theta) = x/1. — Kielelezo\(\PageIndex{5}\): pembetatu kumbukumbu kwa Mfano\(\PageIndex{4}\).

Hivyo,

\ (\ displaystyle\ kuanza {align*}\ dfrac {dx} {\ sqrt {1+x ^ 2}} &=\ dfrac {\ sec ^ 2} {\ sec η} d& &\ maandishi {mbadala} x=\ tan η\\ maandishi {na} dx=\ sec ^ 2\, dη.\\ [4pt]
& & &\ maandishi {Hii inafanya badala}\ sqrt {1+x ^ 2} =\ sec η. \ Nakala {Kurahisisha.}\\ [4pt]
&=\ sec η\, dη & &\ maandishi {Tathmini muhimu.}\\ [4pt]
&=\ ln |\ sec ρ+\ tan |+C & &\ maandishi {Tumia pembetatu ya kumbukumbu ili kueleza matokeo kwa suala la} x.\\ [4pt]
&=\ ln |\ sqrt {1+x ^ 2} +X|+C\ mwisho {align*}\)

Kuangalia suluhisho, tofautisha:

\(\dfrac{d}{dx}\Big( \ln |\sqrt{1+x^2}+x|\Big)=\dfrac{1}{\sqrt{1+x^2}+x}⋅\left(\dfrac{x}{\sqrt{1+x^2}}+1\right) =\dfrac{1}{\sqrt{1+x^2}+x}⋅\dfrac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}=\dfrac{1}{\sqrt{1+x^2}}.\)

Tangu\(\sqrt{1+x^2}+x>0\) kwa maadili yote ya\(x\), tunaweza kuandika upya\( \ln |\sqrt{1+x^2}+x|+C= \ln (\sqrt{1+x^2}+x)+C\), kama taka.

Mfano\(\PageIndex{5}\): Evaluating \(∫\dfrac{dx}{\sqrt{1+x^2}}\) Using a Different Substitution

Tumia badala ya\(x=\sinh θ\) kutathmini\(\displaystyle ∫\dfrac{dx}{\sqrt{1+x^2}}.\)

Suluhisho

Kwa sababu\(\sinh θ\) ina mbalimbali ya idadi yote halisi, na\(1+\sinh^2θ=\cosh^2θ\), tunaweza pia kutumia badala ya\(x=\sinh θ\) kutathmini hii muhimu. Katika kesi hiyo,\(dx=\cosh θ \,dθ.\) Kwa hiyo,

\ (\ displaystyle\ kuanza {align*}\ dfrac {dx} {\ sqrt {1+x ^ 2}}} &=\ dfrac {\ cosh η} {\ sqrt {1+\ sinh ^ 2}} D& &\ maandishi {mbadala} x=\ sinh η\\, dη.\\ [4pt]
& & &\ maandishi {mbadala} 1+\ sinh ^ 2κ=\ cosh^2η.\\ [4pt]
&=\ dfrac {\ cosh η} {\ sqrt {\ cosh^2}}} d& amp; &\ maandishi {tangu}\ sqrt {\ cosh^2} =|\ cosh ρ|\\ [4pt]
&=\ dfrac {\ cosh η} {|\ cosh ρ|} dη & & |\ cosh ρ|=\ cosh η\ maandishi {tangu}\ cosh ρ>0\ maandishi {kwa ajili ya wote} η.\\ [4pt]
&=\ dfrac {\ cosh η} {\ cosh η} dη & &\ maandishi {Kurahisisha.}\\ [4pt]
&=1\, dη & & & \ Nakala {Tathmini muhimu.}\\ [4pt]
&=κ+C & &\ maandishi {Tangu} x=\ sinh η,\ maandishi {tunajua} η =\ sinh^ {-1} x.\\ [4pt]
&=\ sinh^ {-1} x+C.\ mwisho {align*}\)

Uchambuzi

Jibu hili linaonekana tofauti kabisa na jibu lililopatikana\(x=\tan θ.\) kwa kutumia badala Kuona kwamba ufumbuzi ni sawa, kuweka\(y=\sinh^{−1}x\). Hivyo,\(\sinh y=x.\) Kutoka equation hii sisi kupata:

\[\dfrac{e^y−e^{−y}}{2}=x. \nonumber \]

Baada ya kuzidisha pande zote mbili\(2e^y\) na kuandika upya, equation hii inakuwa:

\[e^{2y}−2xe^y−1=0. \nonumber \]

Tumia equation ya quadratic kutatua kwa\(e^y\):

\[e^y=\dfrac{2x±\sqrt{4x^2+4}}{2}. \nonumber \]

Kurahisisha, tuna:

\[e^y=x±\sqrt{x^2+1}. \nonumber \]

Tangu\(x−\sqrt{x^2+1}<0\), ni lazima iwe kesi hiyo\(e^y=x+\sqrt{x^2+1}\). Hivyo,

\[y= \ln (x+\sqrt{x^2+1}). \nonumber \]

Mwisho, tunapata

\[\sinh^{−1}x= \ln (x+\sqrt{x^2+1}). \nonumber \]

Baada ya kufanya uchunguzi wa mwisho kwamba, tangu\(x+\sqrt{x^2+1}>0,\)

\[ \ln (x+\sqrt{x^2+1})= \ln ∣\sqrt{1+x^2}+x∣, \nonumber \]

tunaona kwamba mbinu mbili tofauti zinazozalishwa ufumbuzi sawa.

Mfano\(\PageIndex{6}\): Finding an Arc Length

Pata urefu wa curve\(y=x^2\) juu ya muda\([0,\dfrac{1}{2}]\).

Suluhisho

Kwa sababu\(\dfrac{dy}{dx}=2x\), urefu wa arc hutolewa na

\[∫^{1/2}_0\sqrt{1+(2x)^2}dx=∫^{1/2}_0\sqrt{1+4x^2}dx. \nonumber \]

Ili kutathmini jambo hili muhimu, tumia badala\(x=\dfrac{1}{2}\tan θ\) na\(dx=\tfrac{1}{2}\sec^2θ \, dθ\). Pia tunahitaji kubadilisha mipaka ya ushirikiano. Kama\(x=0\), basi\(θ=0\) na kama\(x=\dfrac{1}{2}\), basi\(θ=\dfrac{π}{4}.\) Hivyo,

\(∫^{1/2}_0\sqrt{1+4x^2}dx=∫^{π/4}_0\sqrt{1+\tan^2θ}\cdot \tfrac{1}{2}\sec^2θ \, dθ\)Baada ya kubadilisha,\(\sqrt{1+4x^2}=\sec θ\). (Mbadala\(1+\tan^2θ=\sec^2θ\) na kurahisisha.)

\(=\tfrac{1}{2}∫^{π/4}_0\sec^3θ \, dθ\)Sisi inayotokana muhimu hii katika sehemu ya awali.

\(=\tfrac{1}{2}(\dfrac{1}{2}\sec θ\tan θ+ \dfrac{1}{2}\ln |\sec θ+\tan θ|)∣^{π/4}_0\)Tathmini na kurahisisha.

\(=\tfrac{1}{4}(\sqrt{2}+ \ln (\sqrt{2}+1)).\)

Zoezi\(\PageIndex{2}\)

Andika upya\(\displaystyle ∫ x^3\sqrt{x^2+4}dx\) kwa kutumia mbadala kuwashirikisha\(\tan θ\).

Kidokezo: Tumia\(x=2\tan θ\) na\(dx=2\sec^2θ \, dθ.\)

Jibu: \[ ∫ 32\tan^3θ\sec^3θ \, dθ \nonumber \]

Kuunganisha Maneno Kuhusisha\(\sqrt{x^2−a^2}\)

Kikoa cha kujieleza\(\sqrt{x^2−a^2}\) ni\((−∞,−a]∪[a,+∞)\). Hivyo, ama\(x\le −a\) au\(x\ge a.\) Hivyo,\(\dfrac{x}{a}≤−1\) au\(\dfrac{x}{a}≥1\). Kwa kuwa vipindi hivi vinahusiana na upeo wa\(\sec θ\) juu ya kuweka\([0,\dfrac{π}{2})∪(\dfrac{π}{2},π]\), ni busara kutumia badala\(\sec θ=\dfrac{x}{a}\) au, sawa\(x=a\sec θ\), wapi\(0≤θ<\dfrac{π}{2}\) au\(\dfrac{π}{2}<θ≤π\). Kubadilisha sambamba kwa\(dx\) ni\(dx=a\sec θ\tan θ \, dθ\). Utaratibu wa kutumia mbadala hii umeelezwa katika mkakati wafuatayo wa kutatua matatizo.

Kutatua matatizo Mkakati: Integrals Kuwashirikisha\(\sqrt{x^2−a^2}\)

Angalia ili uone kama muhimu haiwezi kutathminiwa kwa kutumia njia nyingine. Ikiwa ndivyo, tunaweza kutaka kufikiria kutumia mbinu mbadala.
Mbadala\(x=a\sec θ\) na\(dx=a\sec θ\tan θ \, dθ\). Hii badala ya mavuno\[ \sqrt{x^2−a^2}=\sqrt{(a\sec θ)^2−a^2}=\sqrt{a^2(\sec^2θ-1)}=\sqrt{a^2\tan^2θ}=|a\tan θ|. \nonumber \] Kwa\(x≥a, |a\tan θ|=a\tan θ\) na kwa\(x≤−a, |a\tan θ|=−a\tan θ.\)
Kurahisisha usemi.
Tathmini mbinu muhimu za kutumia kutoka sehemu ya integrals trigonometric.
Tumia pembetatu za kumbukumbu kutoka Kielelezo\(\PageIndex{6}\) ili uandike upya matokeo katika suala la\(x\).
Unaweza pia haja ya kutumia baadhi ya utambulisho trigonometric na uhusiano\(θ=\sec^{−1}\left(\dfrac{x}{a}\right)\). (Kumbuka: Tunahitaji pembetatu zote za kumbukumbu, kwa kuwa maadili ya baadhi ya uwiano wa trigonometric ni tofauti kulingana na kama\(x>a\) au\(x<−a\).)

Takwimu hii ina pembetatu mbili za kulia. Pembetatu ya kwanza iko katika roboduara ya kwanza ya mfumo wa kuratibu xy na ina angle iliyoitwa theta. Pembe hii ni kinyume na upande wa wima. Hypotenuse ni kinachoitwa x, mguu wima ni kinachoitwa mizizi mraba ya (x ^ 2-a ^ 2), na mguu usawa ni kinachoitwa a. mguu usawa ni juu ya x-axis. Kwa upande wa kushoto wa pembetatu ni sec equation (theta) = x/a, x — Kielelezo\(\PageIndex{6}\): Matumizi sahihi rejea pembetatu kueleza kazi trigonometric tathmini\(θ\) katika suala la\(x\).

Mfano\(\PageIndex{7}\): Finding the Area of a Region

Pata eneo la kanda kati ya grafu ya\(f(x)=\sqrt{x^2−9}\) na x-axis juu ya muda\([3,5].\)

Suluhisho

Kwanza, mchoro grafu mbaya ya kanda iliyoelezwa katika tatizo, kama inavyoonekana katika takwimu ifuatayo.

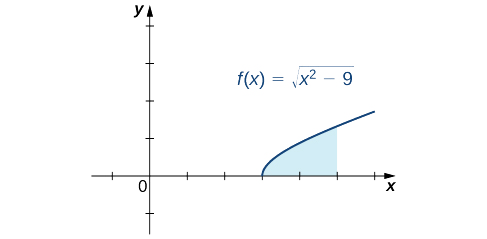
Takwimu hii ni grafu ya kazi f (x) = mizizi ya mraba ya (x ^ 2-9). Ni Curve inayoongezeka inayoanza kwenye x-mhimili saa 3 na iko katika roboduara ya kwanza. Chini ya Curve juu ya x-mhimili ni kanda kivuli imepakana na haki katika x = 5. — Kielelezo\(\PageIndex{7}\): Kuhesabu eneo la mkoa wa kivuli inahitaji kutathmini muhimu na badala ya trigonometric.

Tunaweza kuona kwamba eneo hilo ni\(A=∫^5_3\sqrt{x^2−9}dx\). Kutathmini hii muhimu, mbadala\(x=3\sec θ\) na\(dx=3\sec θ\tan θ \, dθ\). Lazima pia kubadilisha mipaka ya ushirikiano. Ikiwa\(x=3\), basi\(3=3\sec θ\) na hivyo\(θ=0\). Ikiwa\(x=5\), basi\(θ=\sec^{−1}(\dfrac{5}{3})\). Baada ya kufanya mbadala hizi na kurahisisha, tuna

Eneo\(=∫^5_3\sqrt{x^2−9}dx\)

\(=∫^{\sec^{−1}(5/3)}_09\tan^2θ\sec θ \, dθ\)Tumia\(\tan^2θ=\sec^2θ - 1.\)

\(=∫^{\sec^{−1}(5/3)}_09(\sec^2θ−1)\sec θ \, dθ\)Panua.

\(=∫^{\sec^{−1}(5/3)}_09(\sec^3θ−\sec θ)\,dθ\)Tathmini muhimu.

\(=(\dfrac{9}{2} \ln |\sec θ+\tan θ|+\dfrac{9}{2}\sec θ\tan θ)−9 \ln |\sec θ+\tan θ|∣^{\sec^{−1}(5/3)}_0\)Kurahisisha.

\(=\dfrac{9}{2}\sec θ\tan θ−\dfrac{9}{2} \ln |\sec θ+\tan θ|∣^{\sec^{−1}(5/3)}_0\)Tathmini. Tumia\(\sec(\sec^{−1}\dfrac{5}{3})=\dfrac{5}{3}\) na\(\tan(\sec^{−1}\dfrac{5}{3})=\dfrac{4}{3}.\)

\(=\dfrac{9}{2}⋅\dfrac{5}{3}⋅\dfrac{4}{3}−\dfrac{9}{2} \ln ∣\dfrac{5}{3}+\dfrac{4}{3}∣−(\dfrac{9}{2}⋅1⋅0−\dfrac{9}{2} \ln |1+0|)\)

\(=10−\dfrac{9}{2} \ln 3\)

Zoezi\(\PageIndex{3}\)

Kutathmini\[∫\dfrac{dx}{\sqrt{x^2−4}}. \nonumber \] kudhani kwamba\(x>2.\)

Kidokezo: Mbadala\(x=2\sec θ\) na\(dx=2\sec θ\tan θ \, dθ.\)

Jibu: \[ \ln |\dfrac{x}{2}+\dfrac{\sqrt{x^2−4}}{2}|+C \nonumber \]

Dhana muhimu

Kwa integrals kuwashirikisha\(\sqrt{a^2−x^2}\), kutumia badala\(x=a\sin θ\) na\(dx=a\cos θ \, dθ.\)
Kwa integrals kuwashirikisha\(\sqrt{a^2+x^2}\), kutumia badala\(x=a\tan θ\) na\(dx=a\sec^2θ \, dθ\).
Kwa integrals kuwashirikisha\(\sqrt{x^2−a^2}\), mbadala\(x=a\sec θ\) na\(dx=a\sec θ\tan θ \,dθ\).

faharasa

badala ya trigonometric: mbinu ya ushirikiano ambayo inabadilisha sehemu ya algebraic iliyo na maneno ya fomu\(\sqrt{a^2−x^2}\),\(\sqrt{a^2+x^2}\), au\(\sqrt{x^2−a^2}\) katika muhimu ya trigonometric