5.7E: Mazoezi ya Sehemu ya 5.7

Last updated
Save as PDF

Page ID: 178602

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Katika mazoezi ya 1 - 6, tathmini kila muhimu kwa suala la kazi ya trigonometric inverse.

1)$\displaystyle ∫^{\sqrt{3}/2}_0\frac{dx}{\sqrt{1−x^2}}$

Jibu: $\displaystyle ∫^{\sqrt{3}/2}_0\frac{dx}{\sqrt{1−x^2}} \quad = \quad \sin^{−1}x\bigg|^{\sqrt{3}/2}_0=\dfrac{π}{3}$

2)$\displaystyle ∫^{1/2}_{−1/2}\frac{dx}{\sqrt{1−x^2}}$

3)$\displaystyle ∫^1_{\sqrt{3}}\frac{dx}{\sqrt{1+x^2}}$

Jibu: $\displaystyle ∫^1_{\sqrt{3}}\frac{dx}{\sqrt{1+x^2}} \quad = \quad \tan^{−1}x\bigg|^1_{\sqrt{3}}=−\dfrac{π}{12}$

4)$\displaystyle ∫^{\sqrt{3}}_{\frac{1}{\sqrt{3}}}\frac{dx}{1+x^2}$

5)$\displaystyle ∫^{\sqrt{2}}_1\frac{dx}{|x|\sqrt{x^2−1}}$

Jibu: $\displaystyle ∫^{\sqrt{2}}_1\frac{dx}{|x|\sqrt{x^2−1}} \quad = \quad \sec^{−1}x\bigg|^{\sqrt{2}}_1=\dfrac{π}{4}$

6)$\displaystyle ∫^{\frac{2}{\sqrt{3}}}_1\frac{dx}{|x|\sqrt{x^2−1}}$

Katika mazoezi ya 7 - 12, tafuta kila muhimu kwa muda usiojulikana, ukitumia mbadala zinazofaa.

7)$\displaystyle ∫\frac{dx}{\sqrt{9−x^2}}$

Jibu: $\displaystyle ∫\frac{dx}{\sqrt{9−x^2}} \quad = \quad \sin^{−1}\left(\frac{x}{3}\right)+C$

8)$\displaystyle ∫\frac{dx}{\sqrt{1−16x^2}}$

9)$\displaystyle ∫\frac{dx}{9+x^2}$

Jibu: $\displaystyle ∫\frac{dx}{9+x^2} \quad = \quad \frac{1}{3}\tan^{−1}\left(\frac{x}{3}\right)+C$

10)$\displaystyle ∫\frac{dx}{25+16x^2}$

11)$\displaystyle ∫\frac{dx}{x\sqrt{x^2−9}}$

Jibu: $\displaystyle ∫\frac{dx}{x\sqrt{x^2−9}} \quad = \quad \frac{1}{3}\sec^{−1}\left(\frac{|x|}{3}\right)+C$

12)$\displaystyle ∫\frac{dx}{x\sqrt{4x^2−16}}$

13) Eleza uhusiano$\displaystyle −\cos^{−1}t+C=∫\frac{dt}{\sqrt{1−t^2}}=\sin^{−1}t+C.$ Je, ni kweli, kwa ujumla, kwamba$\cos^{−1}t=−\sin^{−1}t$?

Jibu: $\cos(\frac{π}{2}−θ)=\sin θ.$Hivyo,$\sin^{−1}t=\dfrac{π}{2}−\cos^{−1}t.$ Wanatofautiana na mara kwa mara.

14) Eleza uhusiano$\displaystyle \sec^{−1}t+C=∫\frac{dt}{|t|\sqrt{t^2−1}}=−\csc^{−1}t+C.$ Je, ni kweli, kwa ujumla, kwamba$\sec^{−1}t=−\csc^{−1}t$?

15) Eleza ni nini kibaya na muhimu zifuatazo:$\displaystyle ∫^2_1\frac{dt}{\sqrt{1−t^2}}$.

Jibu: $\sqrt{1−t^2}$si hufafanuliwa kama idadi halisi wakati$t>1$.

16) Eleza ni nini kibaya na muhimu zifuatazo:$\displaystyle ∫^1_{−1}\frac{dt}{|t|\sqrt{t^2−1}}$.

Jibu: $\sqrt{t^2−1}$si hufafanuliwa kama idadi halisi wakati$-1 \lt t \lt 1$, na integrand haijulikani wakati$t = -1$ au$t = 1$.

Katika mazoezi 17 - 20, tatua kwa antiderivative ya$f$ na$C=0$, kisha tumia calculator kwa grafu$f$ na antiderivative juu ya muda uliopewa$[a,b]$. Kutambua thamani ya$C$ vile kwamba kuongeza$C$ antiderivative recovers muhimu uhakika$\displaystyle F(x)=∫^x_af(t)\,dt$.

17) [T]$\displaystyle ∫\frac{1}{\sqrt{9−x^2}}\,dx$ juu$[−3,3]$

Jibu

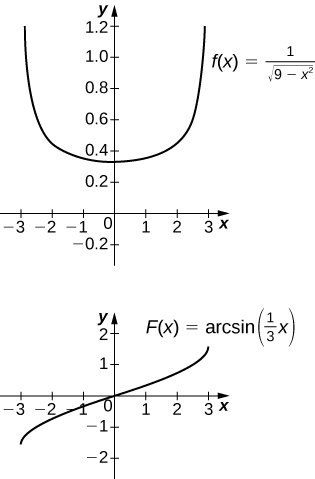
$Grafu mbili. Ya kwanza inaonyesha kazi f (x) = 1/sqrt (9 - x ^ 2). Ni juu ya ufunguzi Curve ulinganifu kuhusu mhimili y, kuvuka saa (0, 1/3). Ya pili inaonyesha kazi F (x) = arcsin (1/3 x). Ni Curve kuongezeka kwenda kwa njia ya asili.$

Antiderivative ni$ \sin^{−1}(\frac{x}{3})+C$. Kuchukua$C=\frac{π}{2}$ recovers muhimu uhakika.

18) [T]$\displaystyle ∫\frac{9}{9+x^2}\,dx$ juu$[−6,6]$

19) [T]$\displaystyle ∫\frac{\cos x}{4+\sin^2x}\,dx$ juu$[−6,6]$

Jibu

$Grafu mbili. Ya kwanza inaonyesha kazi f (x) = cos (x)/(4 + dhambi (x) ^2). Ni kazi ya oscillating juu ya [-6, 6] na pointi za kugeuka kwa takribani (-3, -2.5), (0, .25), na (3, -2.5), ambapo (0, .25) ni max ya ndani na wengine ni dakika za ndani. Ya pili inaonyesha kazi F (x) = .5 * arctan (.5*dhambi (x)), ambayo pia oscillates juu ya [-6,6]. Ina pointi za kugeuka kwa takribani (-4.5, .25), (-1.5, -.25), (1.5, .25), na (4.5, -.25).$

Antiderivative ni$\frac{1}{2}\tan^{−1}(\frac{\sin x}{2})+C$. Kuchukua$C=\frac{1}{2}\tan^{−1}(\frac{\sin(6)}{2})$ recovers muhimu uhakika.

20) [T]$\displaystyle ∫\frac{e^x}{1+e^{2x}}\,dx$ juu$[−6,6]$

Katika mazoezi 21 - 26, compute antiderivative kutumia mbadala sahihi.

21)$\displaystyle ∫\frac{\sin^{−1}t}{\sqrt{1−t^2}}\,dt$

Jibu: $\displaystyle ∫\frac{\sin^{−1}t\,dt}{\sqrt{1−t^2}} \quad = \quad \tfrac{1}{2}(\sin^{−1}t)^2+C$

22)$\displaystyle ∫\frac{dt}{\sin^{−1} t\sqrt{1−t^2}}$

23)$\displaystyle ∫\frac{\tan^{−1}(2t)}{1+4t^2}\,dt$

Jibu: $\displaystyle ∫\frac{\tan^{−1}(2t)}{1+4t^2}\,dt \quad = \quad \frac{1}{4}(\tan^{−1}(2t))^2+C$

24)$\displaystyle ∫\frac{t\tan^{−1}(t^2)}{1+t^4}\,dt$

25)$\displaystyle ∫\frac{\sec^{−1}\left(\tfrac{t}{2}\right)}{|t|\sqrt{t^2−4}}\,dt$

Jibu: $\displaystyle ∫\frac{\sec^{−1}\left(\tfrac{t}{2}\right)}{|t|\sqrt{t^2−4}}\,dt \quad = \quad \tfrac{1}{4}(\sec^{−1}\left(\tfrac{t}{2}\right))^2+C$

26)$\displaystyle ∫\frac{t\sec^{−1}(t^2)}{t^2\sqrt{t^4−1}}\,dt$

Katika mazoezi ya 27 - 32, tumia calculator kwa grafu ya antiderivative ya$f$ na$C=0$ zaidi ya muda$[a,b].$ uliopewa Takriban thamani ya$C$, ikiwa inawezekana, kama vile kuongeza$C$ kwa antiderivative inatoa thamani sawa na muhimu ya uhakika$\displaystyle F(x)=∫^x_af(t)\,dt.$

27) [T]$\displaystyle ∫\frac{1}{x\sqrt{x^2−4}}\,dx$ juu$[2,6]$

Jibu

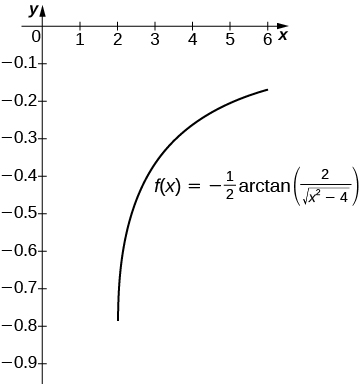
$Grafu ya kazi f (x) = -.5 * arctan (2/(sqrt (x ^ 2 - 4)) katika roboduara nne. Ni concave kuongezeka chini Curve na asymptote wima katika x=2.$

Antiderivative ni$\frac{1}{2}\sec^{−1}(\frac{x}{2})+C$. Kuchukua$C=0$ recovers muhimu uhakika juu ya$ [2,6]$.

28) [T]$\displaystyle ∫\frac{1}{(2x+2)\sqrt{x}}\,dx$ juu$[0,6]$

29) [T]$\displaystyle ∫\frac{(\sin x+x\cos x)}{1+x^2\sin^2x\,dx}$ juu$ [−6,6]$

Jibu

$Grafu ya f (x) = arctan (x dhambi (x)) juu ya [-6,6]. Ina pointi tano za kugeuka kwa takribani (-5, -1.5), (-2,1), (0,0), (2,1), na (5, -1.5).$

Antiderivative ya jumla ni$\tan^{−1}(x\sin x)+C$. Kuchukua$C=−\tan^{−1}(6\sin(6))$ recovers muhimu uhakika.

30) [T]$\displaystyle ∫\frac{2e^{−2x}}{\sqrt{1−e^{−4x}}}\,dx$ juu$[0,2]$

31) [T]$\displaystyle ∫\frac{1}{x+x\ln 2x}$ juu$[0,2]$

Jibu

$Grafu ya kazi f (x) = arctan (ln (x)) juu ya (0, 2]. Ni Curve kuongezeka kwa x-intercept katika (1,0).$

Antiderivative ya jumla ni$\tan^{−1}(\ln x)+C$. Kuchukua$\displaystyle C=\tfrac{π}{2}=\lim_{t \to ∞}\tan^{−1} t$ recovers muhimu uhakika.

32) [T]$\displaystyle ∫\frac{\sin^{−1}x}{\sqrt{1−x^2}}$ juu$[−1,1]$

Katika mazoezi ya 33 - 38, compute kila muhimu kwa kutumia mbadala zinazofaa.

33)$\displaystyle ∫\frac{e^t}{\sqrt{1−e^{2t}}}\,dt$

Jibu: $\displaystyle ∫\frac{e^t}{\sqrt{1−e^{2t}}}\,dt \quad = \quad \sin^{−1}(e^t)+C$

34)$\displaystyle ∫\frac{e^t}{1+e^{2t}}\,dt$

35)$\displaystyle ∫\frac{dt}{t\sqrt{1−\ln^2t}}$

Jibu: $\displaystyle ∫\frac{dt}{t\sqrt{1−\ln^2t}} \quad = \quad \sin^{−1}(\ln t)+C$

36)$\displaystyle ∫\frac{dt}{t(1+\ln^2t)}$

37)$\displaystyle ∫\frac{\cos^{−1}(2t)}{\sqrt{1−4t^2}}\,dt$

Jibu: $\displaystyle ∫\frac{\cos^{−1}(2t)}{\sqrt{1−4t^2}}\,dt \quad = \quad −\frac{1}{2}(\cos^{−1}(2t))^2+C$

38)$\displaystyle ∫\frac{e^t\cos^{−1}(e^t)}{\sqrt{1−e^{2t}}}\,dt$

Katika mazoezi 39 - 42, compute kila muhimu ya uhakika.

39)$\displaystyle ∫^{1/2}_0\frac{\tan(\sin^{−1}t)}{\sqrt{1−t^2}}\,dt$

Jibu: $\displaystyle ∫^{1/2}_0\frac{\tan(\sin^{−1}t)}{\sqrt{1−t^2}}\,dt \quad = \quad \frac{1}{2}\ln\left(\frac{4}{3}\right)$

40)$\displaystyle ∫^{1/2}_{1/4}\frac{\tan(\cos^{−1}t)}{\sqrt{1−t^2}}\,dt$

41)$\displaystyle ∫^{1/2}_0\frac{\sin(\tan^{−1}t)}{1+t^2}\,dt$

Jibu: $\displaystyle ∫^{1/2}_0\frac{\sin(\tan^{−1}t)}{1+t^2}\,dt \quad = \quad 1−\frac{2}{\sqrt{5}}$

42)$\displaystyle ∫^{1/2}_0\frac{\cos(\tan^{−1}t)}{1+t^2}\,dt$

43) Kwa$A>0$, compute$\displaystyle I(A)=∫^{A}_{−A}\frac{dt}{1+t^2}$ na kutathmini$\displaystyle \lim_{a→∞}I(A)$, eneo chini ya grafu ya$\dfrac{1}{1+t^2}$ juu$[−∞,∞]$.

Jibu: $2\tan^{−1}(A)→π$kama$A→∞$

44) Kwa$1<B<∞$, compute$\displaystyle I(B)=∫^B_1\frac{dt}{t\sqrt{t^2−1}}$ na kutathmini$\displaystyle \lim_{B→∞}I(B)$, eneo chini ya grafu ya$\frac{1}{t\sqrt{t^2−1}}$ juu$[1,∞)$.

45) Tumia badala$u=\sqrt{2}\cot x$ na utambulisho wa$1+\cot^2x=\csc^2x$ kutathmini$\displaystyle ∫\frac{dx}{1+\cos^2x}$. (kidokezo: Kuzidisha juu na chini ya integrand na$\csc^2x$.)

Jibu: Kwa kutumia ladha, moja ina$\displaystyle ∫\frac{\csc^2x}{\csc^2x+\cot^2x}\,dx=∫\frac{\csc^2x}{1+2\cot^2x}\,dx.$ Kuweka$u=\sqrt{2}\cot x.$ Kisha,$du=−\sqrt{2}\csc^2x$ na muhimu ni$\displaystyle −\tfrac{1}{\sqrt{2}}∫\frac{du}{1+u^2}=−\tfrac{\sqrt{2}}{2}\tan^{−1}u+C=\tfrac{\sqrt{2}}{2}\tan^{−1}(\sqrt{2}\cot x)+C$. Ikiwa mtu anatumia utambulisho$\tan^{−1}s+\tan^{−1}(\frac{1}{s})=\frac{π}{2}$, basi hii inaweza pia kuandikwa$\tfrac{\sqrt{2}}{2}\tan^{−1}(\frac{\tan x}{\sqrt{2}})+C.$

46) [T] Takriban pointi ambayo grafu ya$f(x)=2x^2−1$ na$g(x)=(1+4x^2)^{−3/2}$ intersect, na takriban eneo kati ya grafu zao sahihi kwa maeneo matatu decimal.

47) [T] Takriban pointi ambayo grafu ya$f(x)=x^2−1$ na$f(x)=x^2−1$ intersect, na takriban eneo kati ya grafu zao sahihi kwa maeneo matatu decimal.

Jibu: $x≈±1.13525.$Makadirio ya mwisho ya kushoto na$N=100$ ni 2.796 na decimals hizi zinaendelea$N=500$.

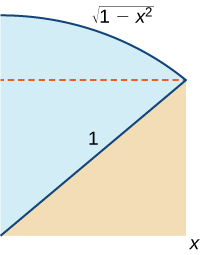
48) Tumia grafu ifuatayo ili kuthibitisha kwamba$\displaystyle ∫^x_0\sqrt{1−t^2}\,dt=\frac{1}{2}x\sqrt{1−x^2}+\frac{1}{2}\sin^{−1}x.$

$Mchoro ulio na maumbo mawili, kabari kutoka kwenye mduara uliovuliwa katika bluu juu ya pembetatu iliyotiwa rangi ya kahawia. Hypotenuse ya pembetatu ni moja ya mipaka ya radii ya kabari ya mduara na ni kitengo 1 kirefu. Kuna mstari mwembamba unaojenga mstatili nje ya sehemu ya kabari na pembetatu, na hypotenuse ya pembetatu kama mshazari wa mstatili. Curve ya mduara inaelezewa na sqrt equation (1-x ^ 2).$