1.2: Madarasa ya Msingi ya Kazi
- Page ID
- 178939
- Tumia mteremko wa kazi ya mstari na kutafsiri maana yake.
- Tambua kiwango cha polynomial.
- Pata mizizi ya polynomial ya quadratic.
- Eleza grafu za kazi za msingi zisizo za kawaida na hata za polynomial.
- Tambua kazi ya busara.
- Eleza grafu za nguvu na kazi za mizizi.
- Eleza tofauti kati ya kazi za algebraic na transcendental.
- Graph kazi kipande defined.
- Mchoro grafu ya kazi ambayo imebadilishwa, imetambulishwa, au inaonekana kutoka kwenye nafasi yake ya awali ya grafu.
Tumejifunza sifa za jumla za kazi, kwa hiyo sasa hebu tuchunguze madarasa maalum ya kazi. Tunaanza kwa kuchunguza mali ya msingi ya kazi za mstari na quadratic, na kisha kuzalisha kuingiza polynomials ya juu. Kwa kuchanganya kazi za mizizi na polynomials, tunaweza kufafanua kazi za jumla za algebraic na kuzitofautisha kutoka kwa kazi za transcendental tunachunguza baadaye katika sura hii. Tunamaliza sehemu hiyo kwa mifano ya kazi zilizoelezwa na kipande na kuangalia jinsi ya kuchora grafu ya kazi ambayo imebadilishwa, imetambulishwa, au inaonekana kutoka kwa fomu yake ya awali.
Kazi za mstari na mteremko
Aina rahisi ya kazi ya kuzingatia ni kazi ya mstari. Kazi za mstari zina fomu\(f(x)=ax+b\), wapi\(a\) na\(b\) ni mara kwa mara. Katika Kielelezo\(\PageIndex{1}\), tunaona mifano ya kazi linear wakati ni chanya, hasi, na sifuri. Kumbuka kwamba ikiwa\(a>0\), grafu ya mstari inaongezeka kama\(x\) ongezeko. Kwa maneno mengine,\(f(x)=ax+b\) ni kuongeza juu ya\((−∞, ∞)\). Ikiwa\(a<0\), grafu ya mstari huanguka kama\(x\) ongezeko. Katika kesi hiyo,\(f(x)=ax+b\) inapungua\((−∞, ∞)\). Ikiwa\(a=0\), mstari ni usawa.
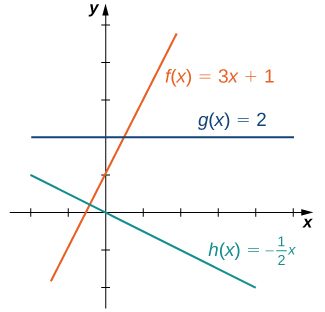
Kama ilivyopendekezwa na Kielelezo\(\PageIndex{1}\), grafu ya kazi yoyote ya mstari ni mstari. Moja ya vipengele vya kutofautisha vya mstari ni mteremko wake. Mteremko ni mabadiliko katika\(y\) kila mabadiliko ya kitengo\(x\). Mteremko hupima mwinuko na mwelekeo wa mstari. Ikiwa mteremko ni chanya, mstari unaonyesha juu wakati wa kusonga kutoka kushoto kwenda kulia. Ikiwa mteremko ni hasi, mstari unaonyesha chini wakati wa kusonga kutoka kushoto kwenda kulia. Ikiwa mteremko ni sifuri, mstari ni usawa. Ili kuhesabu mteremko wa mstari, tunahitaji kuamua uwiano wa mabadiliko katika\(y\) dhidi ya mabadiliko\(x\). Kwa kufanya hivyo, tunachagua pointi mbili\((x_1,y_1)\) na\((x_2,y_2)\) kwenye mstari na tuhesabu\(\dfrac{y_2−y_1}{x_2−x_1}\). Katika Kielelezo\(\PageIndex{2}\), tunaona uwiano huu ni huru ya pointi zilizochaguliwa.
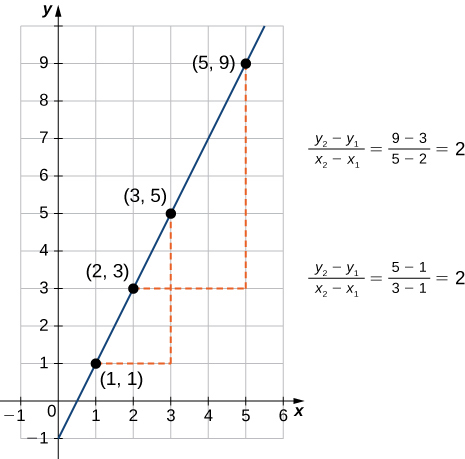
Fikiria mstari\(L\) unaopitia pointi\((x_1,y_1)\) na\((x_2,y_2)\). Hebu\(Δy=y_2−y_1\) na\(Δx=x_2−x_1\) ueleze mabadiliko\(y\) na\(x\), kwa mtiririko huo. Mteremko wa mstari ni
\[m=\dfrac{y_2−y_1}{x_2−x_1}=\dfrac{Δy}{Δx} \nonumber \]
Sasa tunachunguza uhusiano kati ya mteremko na formula ya kazi ya mstari. Fikiria kazi ya mstari iliyotolewa na formula\(f(x)=ax+b\). Kama ilivyojadiliwa hapo awali, tunajua grafu ya kazi linear inapewa na mstari. Tunaweza kutumia ufafanuzi wetu wa mteremko kuhesabu mteremko wa mstari huu. Kama inavyoonekana, tunaweza kuamua mteremko\((y_2−y_1)/(x_2−x_1)\) kwa kuhesabu kwa pointi yoyote\((x_1,y_1)\) na\((x_2,y_2)\) kwenye mstari. Kutathmini kazi\(f\) katika\(x=0\), tunaona kwamba\((0,b)\) ni hatua juu ya mstari huu. Kutathmini kazi hii katika\(x=1\), tunaona kwamba pia\((1,a+b)\) ni uhakika juu ya mstari huu. Kwa hiyo, mteremko wa mstari huu ni
\[\dfrac{(a+b)−b}{1−0}=a. \nonumber \]
Tumeonyesha kuwa mgawo\(a\) ni mteremko wa mstari. Tunaweza kuhitimisha kwamba formula\(f(x)=ax+b\) inaelezea mstari na mteremko\(a\). Zaidi ya hayo, kwa sababu mstari huu intersects\(y\) -axis katika hatua\((0,b)\), tunaona kwamba\(y\) -intercept kwa kazi hii linear ni\((0,b)\). Tunahitimisha kwamba formula\(f(x)=ax+b\) inatuambia mteremko\(a\),, na\(y\) -intercept\((0,b)\),, kwa mstari huu. Kwa kuwa mara nyingi tunatumia ishara\(m\) ili kutaja mteremko wa mstari, tunaweza kuandika
\[\underbrace{f(x)=mx+b}_{\text{slope-intercept form}} \nonumber \]
ili kuashiria fomu ya kuingilia mteremko wa kazi ya mstari.
Wakati mwingine ni rahisi kuelezea kazi ya mstari kwa njia tofauti. Kwa mfano, tuseme grafu ya kazi ya mstari hupita kupitia hatua\((x_1,y_1)\) na mteremko wa mstari ni\(m\). Kwa kuwa hatua nyingine yoyote\((x,f(x))\) kwenye grafu ya\(f\) lazima kukidhi equation
\[m=\dfrac{f(x)−y_1}{x−x_1}, \nonumber \]
kazi hii ya mstari inaweza kuelezwa kwa kuandika
\[\underbrace{f(x)−y_1=m(x−x_1)}_{\text{point-slope equation}}. \nonumber \]
Tunaita equation hii equation uhakika-mteremko kwa kazi hiyo linear.
Kwa kuwa kila mstari usio na wima ni grafu ya kazi ya mstari, pointi kwenye mstari usio na wima zinaweza kuelezewa kwa kutumia usawa wa mteremko au hatua ya mteremko. Hata hivyo, mstari wa wima haukuwakilisha grafu ya kazi na hauwezi kuonyeshwa katika mojawapo ya fomu hizi. Badala yake, mstari wima ni ilivyoelezwa na equation\(x=k\) kwa baadhi ya mara kwa mara\(k\). Kwa kuwa fomu ya kuingilia mteremko wala fomu ya mteremko inaruhusu mistari ya wima, tunatumia notation
\[\underbrace{ax+by=c}_{\text{standard form}}, \nonumber \]
\(a,b\)wapi wote si sifuri, kuashiria fomu ya kawaida ya mstari.
Fikiria mstari unaopita kupitia hatua\((x_1,y_1)\) na mteremko\(m\). equation
\[y−y_1=m(x−x_1) \nonumber \]
ni hatua ya mteremko equation kwa mstari huo.
Fikiria mstari na mteremko\(m\) na\(y\) -intercept\((0,b).\) equation
\[y=mx+b \nonumber \]
ni equation kwa mstari huo katika mteremka-intercept fomu.
Fomu ya kawaida ya mstari hutolewa na equation
\[ax+by=c, \nonumber \]
wapi\(a\) na\(b\) wote si sifuri. Fomu hii ni ya jumla kwa sababu inaruhusu mstari wa wima,\(x=k\).
Fikiria mstari unaopita kupitia pointi\((11,−4)\) na\((−4,5)\), kama inavyoonekana kwenye Kielelezo\(\PageIndex{3}\).
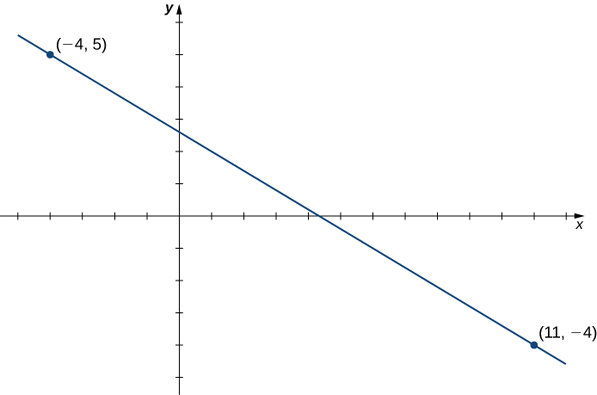
- Pata mteremko wa mstari.
- Kupata equation kwa ajili ya kazi hii linear katika hatua mteremko fomu.
- Kupata equation kwa ajili ya kazi hii linear katika mteremka-intercept fomu.
Suluhisho
1. Mteremko wa mstari ni
\[m=\dfrac{y_2−y_1}{x_2−x_1}=\dfrac{5−(−4)}{−4−11}=−\dfrac{9}{15}=−\dfrac{3}{5}. \nonumber \]
2. Ili kupata equation kwa kazi ya mstari katika fomu ya mteremko wa uhakika, tumia mteremko\(m=−3/5\) na uchague hatua yoyote kwenye mstari. Kama sisi kuchagua uhakika\((11,−4)\), sisi kupata equation
\[f(x)+4=−\dfrac{3}{5}(x−11). \nonumber \]
3. Ili kupata equation kwa ajili ya kazi linear katika mteremka-intercept fomu, kutatua equation katika sehemu\(f(x)\) b. kwa. Tunapofanya hivyo, tunapata equation
\[f(x)=−\dfrac{3}{5}x+\dfrac{13}{5}. \nonumber \]
Fikiria mstari unaopita kupitia pointi\((−3,2)\) na\((1,4)\).
- Pata mteremko wa mstari.
- Pata equation ya mstari huo katika fomu ya mteremko wa uhakika.
- Kupata equation ya mstari kwamba katika mfumo mteremka-intercept.
- Kidokezo
-
Mteremko\(m=Δy/Δx\).
- Jibu
-
\(m=1/2\).
- Jibu b
-
Fomu ya mteremko wa uhakika ni\(y−4=\dfrac{1}{2}(x−1)\).
- Jibu c
-
Fomu ya kuingilia mteremko ni\(y=\dfrac{1}{2}x+\dfrac{7}{2}\).
Jessica anaondoka nyumbani kwake saa 5:50 a.m na huenda kwa mbio ya maili 9. Anarudi nyumbani kwake saa 7:08 a.m. Jibu maswali yafuatayo, akidhani Jessica anaendesha kwa kasi ya mara kwa mara.
- Eleza umbali\(D\) (katika maili) Jessica anaendesha kama kazi linear ya muda wake kukimbia\(t\) (katika dakika).
- Mchoro grafu ya\(D\).
- Tafsiri maana ya mteremko.
Suluhisho
kwa wakati\(t=0\), Jessica yuko nyumbani kwake, hivyo\(D(0)=0\). Wakati wa\(t=78\) dakika, Jessica amemaliza mbio\(9\) mi, hivyo\(D(78)=9\). Mteremko wa kazi ya mstari ni
\[m=\dfrac{9−0}{78−0}=\dfrac{3}{26}.\nonumber \]
\(y\)-intercept ni\((0,0)\), hivyo equation kwa kazi hii linear ni
\[D(t)=\dfrac{3}{26}t. \nonumber \]
b Kwa grafu\(D\), tumia ukweli kwamba grafu hupita kupitia asili na ina mteremko\(m=3/26.\)
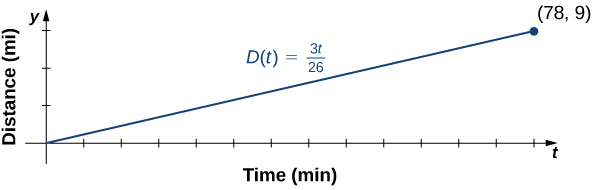
c. mteremko\(m=3/26≈0.115\) inaelezea umbali (katika maili) Jessica anaendesha kwa dakika, au kasi yake wastani.
Polynomials
Kazi ya mstari ni aina maalum ya darasa la jumla la kazi: polynomials. Kazi ya polynomial ni kazi yoyote ambayo inaweza kuandikwa kwa fomu
\[f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0 \nonumber \]
kwa baadhi integer\(n≥0\) na constants\(a_n,a_{n−1},…,a_0\), ambapo\(a_n≠0\). Katika kesi wakati\(n=0\), sisi kuruhusu\(a_0=0\); kama\(a_0=0\), kazi\(f(x)=0\) inaitwa kazi sifuri. Thamani\(n\) inaitwa kiwango cha polynomial; mara kwa mara\(a_n\) inaitwa mgawo wa kuongoza. Kazi ya mstari wa fomu\(f(x)=mx+b\) ni polynomial ya shahada 1 ikiwa\(m≠0\) na shahada 0 ikiwa\(m=0\). Polynomial ya shahada 0 pia inaitwa kazi ya mara kwa mara. Kazi ya polynomial ya shahada ya 2 inaitwa kazi ya quadratic. Hasa, kazi ya quadratic ina fomu
\[f(x)=ax^2+bx+c, \nonumber \]
wapi\(a≠0\). Kazi ya polynomial ya shahada\(3\) inaitwa kazi ya ujazo.
Kazi za Nguvu
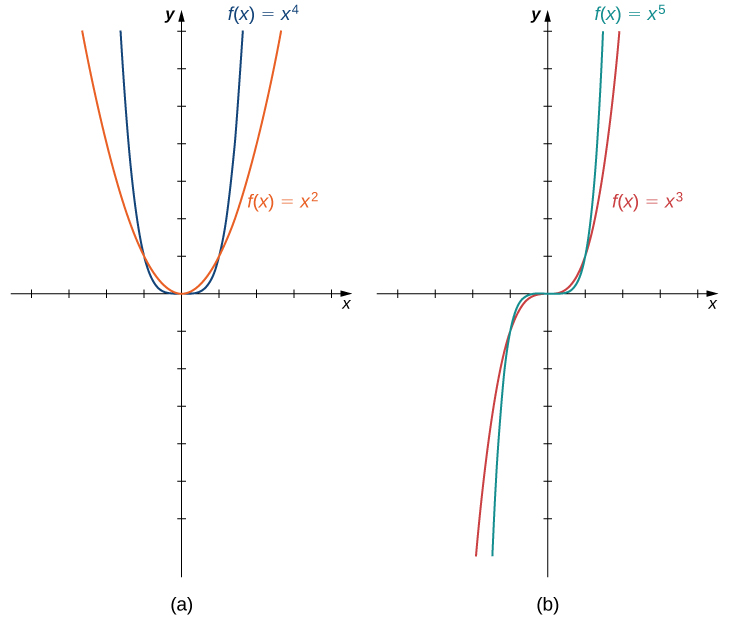
Baadhi ya kazi za polynomial ni kazi za nguvu. Kazi ya nguvu ni kazi yoyote ya fomu\(f(x)=ax^b\), wapi\(a\) na\(b\) ni idadi yoyote halisi. Mtazamaji katika kazi ya nguvu inaweza kuwa nambari yoyote halisi, lakini hapa tunazingatia kesi wakati exponent ni integer chanya. (Tunazingatia kesi nyingine baadaye.) Ikiwa exponent ni integer chanya, basi\(f(x)=ax^n\) ni polynomial. Kama\(n\) ni hata, basi\(f(x)=ax^n\) ni hata kazi kwa sababu\(f(−x)=a(−x)^n=ax^n\) kama\(n\) ni hata. Kama\(n\) ni isiyo ya kawaida, basi\(f(x)=ax^n\) ni kazi isiyo ya kawaida kwa sababu\(f(−x)=a(−x)^n=−ax^n\) kama\(n\) ni isiyo ya kawaida (Kielelezo\(\PageIndex{4}\)).
Tabia katika Infinity
Kuamua tabia ya kazi\(f\) kama pembejeo mbinu infinity, sisi kuangalia maadili\(f(x)\) kama pembejeo\(x\), kuwa kubwa. Kwa kazi fulani, maadili ya\(f(x)\) mbinu ya idadi ya mwisho. Kwa mfano, kwa ajili ya kazi\(f(x)=2+1/x\), maadili\(1/x\) kuwa karibu na karibu na sifuri kwa maadili yote ya\(x\) kama wao kupata kubwa na kubwa. Kwa kazi hii, tunasema “\(f(x)\)mbinu mbili kama\(x\) inakwenda infinity,” na sisi kuandika\(f(x)→2\) kama\(x→∞\). Mstari\(y=2\) ni asymptote ya usawa kwa kazi\(f(x)=2+1/x\) kwa sababu grafu ya kazi inapata karibu na mstari kama\(x\) inapata kubwa.
Kwa kazi nyingine, maadili\(f(x)\) hayawezi kufikia idadi ya mwisho lakini badala yake inaweza kuwa kubwa kwa maadili yote ya\(x\) kama wao kupata kubwa. Katika hali hiyo, tunasema “\(f(x)\)mbinu infinity kama\(x\) mbinu infinity,” na sisi kuandika\(f(x)→∞\) kama\(x→∞\). Kwa mfano, kwa ajili ya kazi\(f(x)=3x^2\), matokeo\(f(x)\) kuwa kubwa kama pembejeo\(x\) kupata kubwa. Tunaweza kuhitimisha kwamba kazi\(f(x)=3x^2\) inakaribia infinity kama\(x\) mbinu infinity, na sisi kuandika\(3x^2→∞\) kama\(x→∞\). Tabia kama\(x→−∞\) na maana ya\(f(x)→−∞\) kama\(x→∞\) au\(x→−∞\) inaweza kuelezwa sawa. Tunaweza kuelezea nini kinatokea kwa maadili ya\(f(x)\) kama\(x→∞\) na\(x→−∞\) kama tabia ya mwisho ya kazi.
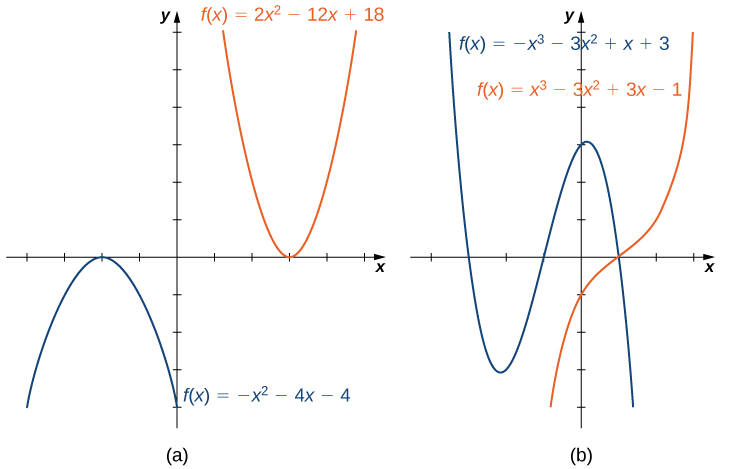
Ili kuelewa tabia ya mwisho kwa kazi nyingi, tunaweza kuzingatia kazi za quadratic na za ujazo. Tabia ya polynomials ya juu ya shahada inaweza kuchambuliwa sawa. Fikiria kazi ya quadratic\(f(x)=ax^2+bx+c\). Kama\(a>0\), maadili\(f(x)→∞\) kama\(x→±∞\). Kama\(a<0\), maadili\(f(x)→−∞\) kama\(x→±∞\). Kwa kuwa grafu ya kazi ya quadratic ni parabola, parabola inafungua juu ikiwa\(a>0\).; parabola inafungua chini ikiwa\(a<0\) (Kielelezo\(\PageIndex{5a}\)).
Sasa fikiria kazi ya ujazo\(f(x)=ax^3+bx^2+cx+d\). Ikiwa\(a>0\), basi\(f(x)→∞\) kama\(x→∞\) na\(f(x)→−∞\) kama\(x→−∞\). Ikiwa\(a<0\), basi\(f(x)→−∞\) kama\(x→∞\) na\(f(x)→∞\) kama\(x→−∞\). Kama tunaweza kuona kutoka kwa grafu hizi mbili, muda wa kuongoza wa polynomial huamua tabia ya mwisho (Kielelezo\(\PageIndex{5b}\)).
Zero za Kazi za Polynomial
Tabia nyingine ya grafu ya kazi ya polynomial ni wapi inapita\(x\) -axis. Kuamua ambapo kazi\(f\) intersects\(x\) -axis, tunahitaji kutatua equation\(f(x)=0\) kwa\(x\). Katika kesi ya kazi ya mstari\(f(x)=mx+b\),\(x\) -intercept hutolewa kwa kutatua equation\(mx+b=0\). Katika kesi hii, tunaona kwamba\(x\) -intercept inatolewa na\((−b/m,0)\). Katika kesi ya kazi ya quadratic, kutafuta\(x\) -intercept (s) inahitaji kutafuta zero za equation quadratic:\(ax^2+bx+c=0\). Katika hali nyingine, ni rahisi kuzingatia polynomial\(ax^2+bx+c\) kupata zero. Ikiwa sio, tunatumia formula ya quadratic.
Fikiria equation quadratic
\[ax^2+bx+c=0, \nonumber \]
wapi\(a≠0\). Ufumbuzi wa equation hii hutolewa na formula ya quadratic
\[x=\dfrac{−b±\sqrt{b^2−4ac}}{2a}. \label{quad} \]
Kama ubaguzi\(b^2−4ac>0\), Equation\ ref {quad} inatuambia kuna namba mbili halisi zinazotimiza equation quadratic. Kama\(b^2−4ac=0\), formula hii inatuambia kuna ufumbuzi moja tu, na ni idadi halisi. Kama\(b^2−4ac<0\), hakuna idadi halisi kukidhi equation quadratic.
Katika kesi ya polynomials ya kiwango cha juu, inaweza kuwa ngumu zaidi kuamua wapi grafu inakabiliana na\(x\) -axis. Katika baadhi ya matukio, inawezekana kupata\(x\) -intercepts kwa kuzingatia polynomial kupata zero zake. Katika hali nyingine, haiwezekani kuhesabu maadili halisi ya\(x\) -intercepts. Hata hivyo, kama tunavyoona baadaye katika maandiko, katika hali kama hii, tunaweza kutumia zana za uchambuzi kwa takriban (kwa kiwango cha juu sana) ambapo\(x\) -intercepts iko. Hapa tunazingatia grafu za polynomials ambazo tunaweza kuhesabu zero zao wazi.
Kwa kazi zifuatazo,
- \(f(x)=−2x^2+4x−1\)
- \(f(x)=x^3−3x^2−4x\)
- kuelezea tabia ya\(f(x)\) kama\(x→±∞\),
- kupata zeros wote wa\(f\), na
- mchoro grafu ya\(f\).
Suluhisho
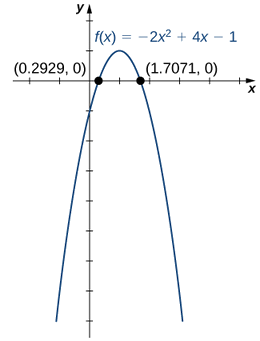
1. Kazi\(f(x)=−2x^2+4x−1\) ni kazi ya quadratic.
1. Kwa sababu\(a=−2<0\), kama\(x→±∞,f(x)→−∞.\)
2. Ili kupata zero za\(f\), tumia formula ya quadratic. Zero ni
\(x=\dfrac{−4±\sqrt{4^2−4(−2)(−1)}}{2(−2)}=\dfrac{−4±\sqrt{8}}{−4}=\dfrac{−4±2\sqrt{2}}{−4}=\dfrac{2±\sqrt{2}}{2}.\)
3. Kwa mchoro grafu ya\(f\), kutumia taarifa kutoka majibu yako ya awali na kuchanganya na ukweli kwamba grafu ni parabola kufungua chini.
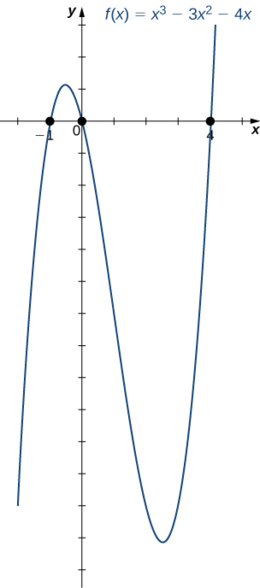
2. Kazi\(f(x)=x^3−3x^2−4x\) ni kazi ya ujazo.
1. Kwa sababu\(a=1>0\), kama\(x→∞\),\(f(x)→∞\). Kama\(x→−∞\),\(f(x)→−∞\).
2. Ili kupata zero za\(f\), tunahitaji kuzingatia polynomial. Kwanza, wakati sisi sababu\(x\) nje ya masharti yote, tunaona
\(f(x)=x(x^2−3x−4).\)
Kisha, tunapofanya kazi ya quadratic\(x^2−3x−4\), tunapata
\(f(x)=x(x−4)(x+1).\)
Kwa hiyo, zero za\(f\) ni\(x=0,4,−1\).
3. Kuchanganya matokeo kutoka sehemu i. na ii., kuteka mchoro mbaya wa\(f\).
Fikiria quadratic kazi\(f(x)=3x^2−6x+2.\) Kupata zero ya\(f\). Je, parabola inafungua juu au chini?
- Kidokezo
-
Tumia formula ya quadratic.
- Jibu
-
Zero ni\(x=1±\sqrt{3}/3\). Parabola inafungua juu.
Mifano ya hisabati
Aina kubwa ya hali halisi ya ulimwengu inaweza kuelezewa kwa kutumia mifano ya hisabati. Mfano wa hisabati ni njia ya kuiga hali halisi ya maisha na milinganyo ya hisabati. Wafizikia, wahandisi, wanauchumi, na watafiti wengine huendeleza mifano kwa kuchanganya uchunguzi na data za kiasi ili kuendeleza milinganyo, kazi, grafu, na zana zingine za hisabati kuelezea tabia ya mifumo mbalimbali kwa usahihi. Mifano ni muhimu kwa sababu husaidia kutabiri matokeo ya baadaye. Mifano ya mifano ya hisabati ni pamoja na utafiti wa mienendo ya idadi ya watu, uchunguzi wa mifumo ya hali ya hewa, na utabiri wa mauzo ya bidhaa.
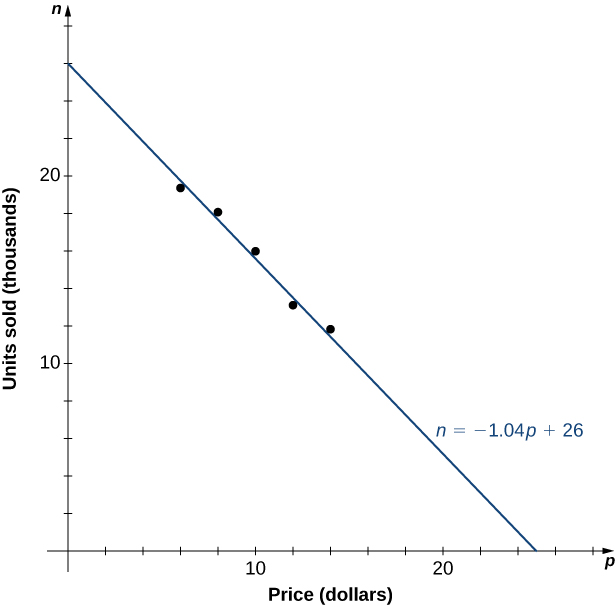
Kwa mfano, hebu tuchunguze mfano wa hisabati ambao kampuni inaweza kutumia kuelezea mapato yake kwa uuzaji wa kipengee fulani. Kiasi\(R\) cha mapato ambayo kampuni inapokea kwa uuzaji wa\(n\) vitu vinavyouzwa kwa bei ya\(p\) dola kwa kila kipengee kinaelezewa na equation\(R=p⋅n\). Kampuni hiyo inavutiwa na jinsi mauzo yanavyobadilika kama bei ya bidhaa inavyobadilika. Tuseme data katika Jedwali\(\PageIndex{1}\) inaonyesha idadi ya vitengo kampuni inauza kama kazi ya bei kwa kila kitu.
| \(p\) | 6 | 8 | 10 | 12 | 14 |
|---|---|---|---|---|---|
| \(n\) | 19.4 | 18.5 | 16.2 | 13.8 | 12.2 |
Katika Kielelezo\(\PageIndex{6}\), tunaona grafu idadi ya vitengo kuuzwa (kwa maelfu) kama kazi ya bei (kwa dola). Tunaona kutoka sura ya grafu kwamba idadi ya vitengo kuuzwa ni uwezekano kazi linear ya bei kwa kila kitu, na data inaweza kuwa karibu approximated na kazi linear\(n= −1.04p+26\) kwa\(0≤p≤25\), ambapo\(n\) anatabiri idadi ya vitengo kuuzwa katika maelfu. Kutumia kazi hii ya mstari, mapato (kwa maelfu ya dola) yanaweza kuhesabiwa na kazi ya quadratic
\[R(p)=p⋅ (−1.04p+26)=−1.04p^2+26p \text{ for }0≤p≤25. \nonumber \]
Katika Mfano\(\PageIndex{4}\), tunatumia kazi hii ya quadratic kutabiri kiasi cha mapato ambayo kampuni inapata kulingana na bei ya mashtaka ya kampuni kwa kila kitu. Kumbuka kwamba hatuwezi kuhitimisha uhakika idadi halisi ya vitengo kuuzwa kwa maadili ya\(p\), ambayo hakuna data zilizokusanywa. Hata hivyo, kutokana na maadili mengine data na grafu inavyoonekana, inaonekana busara kwamba idadi ya vitengo kuuzwa (kwa maelfu) kama bei kushtakiwa ni\(p\) dola inaweza kuwa karibu na maadili alitabiri na kazi linear\(n=−1.04p+26.\)
Kampuni ina nia ya kutabiri kiasi cha mapato ambayo itapokea kulingana na bei ambayo inashutumu kwa kipengee fulani. Kutumia data kutoka Jedwali\(\PageIndex{1}\), kampuni inakuja kwenye kazi inayofuata ya quadratic ili kutengeneza mapato\(R\) kama kazi ya bei kwa kila kipengee\(p:\)
\[R(p)=p⋅(−1.04p+26)=−1.04p^2+26p \nonumber \]
kwa\(0≤p≤25\).
- Kutabiri mapato kama kampuni anauza bidhaa kwa bei ya\(p=$5\) na\(p=$17\).
- Pata zero za kazi hii na ufafanue maana ya zero.
- Mchoro grafu ya\(R\).
- Matumizi grafu kuamua thamani ya\(p\) kwamba maximizes mapato. Kupata mapato ya kiwango cha juu.
Suluhisho
a. kutathmini kazi ya mapato katika\(p=5\) na\(p=17\), tunaweza kuhitimisha kwamba
\(R(5)=−1.04(5)^2+26(5)=104,\text{ so revenue}=$104,000;\)
\(R(17)=−1.04(17)^2+26(17)=141.44,\text{ so revenue}=$141,440.\)
b. zero za kazi hii zinaweza kupatikana kwa kutatua equation\(−1.04p^2+26p=0\). Tunapoelezea kujieleza kwa quadratic, tunapata\(p(−1.04p+26)=0\). Ufumbuzi wa equation hii hutolewa na\(p=0,25\). Kwa maadili haya ya\(p\), mapato ni sifuri. Wakati\(p=$0\), mapato ni sifuri kwa sababu kampuni inatoa bidhaa zake kwa bure. Wakati\(p=$25\), mapato ni sifuri kwa sababu bei ni kubwa mno, na hakuna mtu kununua vitu yoyote.
c Kujua ukweli kwamba kazi ni quadratic, tunajua pia grafu ni parabola. Kwa kuwa mgawo wa kuongoza ni hasi, parabola inafungua chini. Mali moja ya parabolas ni kwamba wao ni symmetric kuhusu mhimili wa ulinganifu, hivyo tangu zero ni katika\(p=0\) na\(p=25\), parabola lazima linganifu kuhusu mstari nusu kati yao, au\(p=12.5\).
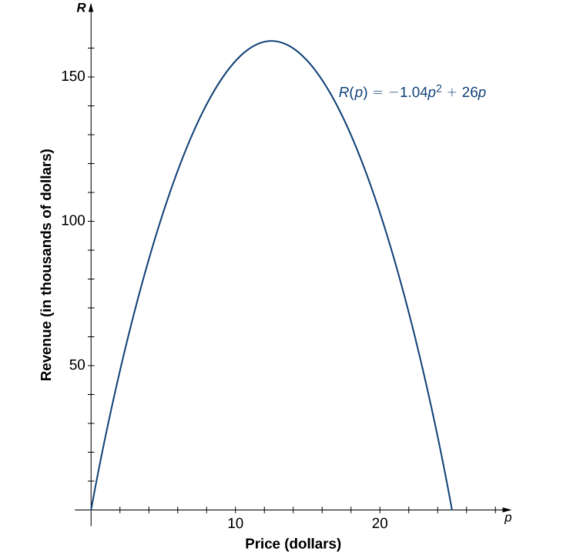
d. kazi ni parabola na zero katika\(p=0\) na\(p=25\), na ni symmetric kuhusu mstari\(p=12.5\), hivyo mapato ya kiwango cha juu hutokea kwa bei ya\(p=$12.50\) kila kitu. Kwa bei hiyo, mapato ni\(R(p)=−1.04(12.5)^2+26(12.5)=$162,500.\)
Kazi za Aljebra
Kwa kuruhusu quotients na nguvu za sehemu katika kazi nyingi, tunaunda darasa kubwa la kazi. Kazi ya algebraic ni moja ambayo inahusisha kuongeza, kuondoa, kuzidisha, mgawanyiko, nguvu za busara, na mizizi. Aina mbili za kazi za algebraic ni kazi za busara na kazi za mizizi.
Kama vile namba za busara ni quotients ya integers, kazi za busara ni quotients ya polynomials. Hasa, kazi ya busara ni kazi yoyote ya fomu\(f(x)=p(x)/q(x)\), wapi\(p(x)\) na\(q(x)\) ni polynomials. Kwa mfano,
\(f(x)=\dfrac{3x−1}{5x+2}\)na\(g(x)=\dfrac{4}{x^2+1}\)
ni kazi ya busara. Kazi ya mizizi ni kazi ya nguvu ya fomu\(f(x)=x^{1/n}\), ambapo\(n\) ni integer nzuri zaidi kuliko moja. Kwa mfano,\(f(x)=x^{1/2}=\sqrt{x}\) ni kazi ya mizizi ya mraba na\(g(x)=x^{1/3}=\sqrt[3]{x}\) ni kazi ya mizizi ya mchemraba. Kwa kuruhusu nyimbo za kazi za mizizi na kazi za busara, tunaweza kuunda kazi nyingine za algebraic. Kwa mfano,\(f(x)=\sqrt{4−x^2}\) ni kazi ya algebraic.
Kwa kila kazi zifuatazo, tafuta kikoa na upeo.
- \(f(x)=\dfrac{3x−1}{5x+2}\)
- \(f(x)=\sqrt{4−x^2}\)
Suluhisho
1. Haiwezekani kugawanya na sifuri, hivyo uwanja ni seti ya namba halisi\(x\) kama hiyo\(x≠−2/5\). Ili kupata upeo, tunahitaji kupata maadili\(y\) ambayo kuna idadi halisi\(x\) kama hiyo
\(y=\dfrac{3x−1}{5x+2}\)
Wakati sisi kuzidisha pande zote mbili za equation hii na\(5x+2\), tunaona kwamba\(x\) lazima kukidhi equation
\(5xy+2y=3x−1.\)
Kutokana na equation hii, tunaweza kuona kwamba\(x\) lazima kukidhi
\(2y+1=x(3−5y).\)
Kama y =\(3/5\), equation hii haina ufumbuzi. Kwa upande mwingine, kwa muda mrefu kama\(y≠3/5\),
\(x=\dfrac{2y+1}{3−5y}\)
satisfies equation hii. Tunaweza kuhitimisha kwamba mbalimbali ya\(f\) ni\(\{y\,|\,y≠3/5\}\).
2. Ili kupata uwanja wa\(f\), tunahitaji\(4−x^2≥0\). Wakati sisi sababu, sisi kuandika\(4−x^2=(2−x)(2+x)≥0\). Ukosefu huu unashikilia ikiwa na tu ikiwa maneno yote mawili ni chanya au maneno yote mawili ni hasi. Kwa suala zote mbili kuwa chanya, tunahitaji kupata\(x\) vile
\(2−x≥0\)na\(2+x≥0.\)
Hizi kukosekana kwa usawa mbili kupunguza\(2≥x\) na\(x≥−2\). Kwa hiyo, kuweka\(\{x\,|\,−2≤x≤2\}\) lazima iwe sehemu ya kikoa. Kwa maneno yote kuwa hasi, tunahitaji
\(2−x≤0\)na\(2+x\le 0.\)
Hizi kukosekana kwa usawa mbili pia kupunguza\(2≤x\) na\(x\le −2\). Hakuna maadili ya\(x\) kwamba kukidhi wote wa kutofautiana hizi. Hivyo, tunaweza kuhitimisha uwanja wa kazi hii ni\(\{x\,|\,−2≤x≤2\}.\)
Ikiwa\(−2≤x≤2\), basi\(0≤4−x^2≤4\). Kwa hiyo\(0≤\sqrt{4−x2}≤2\),, na aina mbalimbali\(f\) ni\(\{y\,|\,0≤y≤2\}.\)
Pata kikoa na upeo wa kazi\(f(x)=(5x+2)/(2x−1).\)
- Kidokezo
-
Denominator haiwezi kuwa sifuri. Kutatua equation\(y=(5x+2)/(2x−1)\)\(x\) kwa kupata mbalimbali.
- Jibu
-
Domain ni seti ya idadi halisi\(x\) kama hiyo\(x≠1/2\). Mipangilio ni kuweka\(\{y\,|\,y≠5/2\}\).
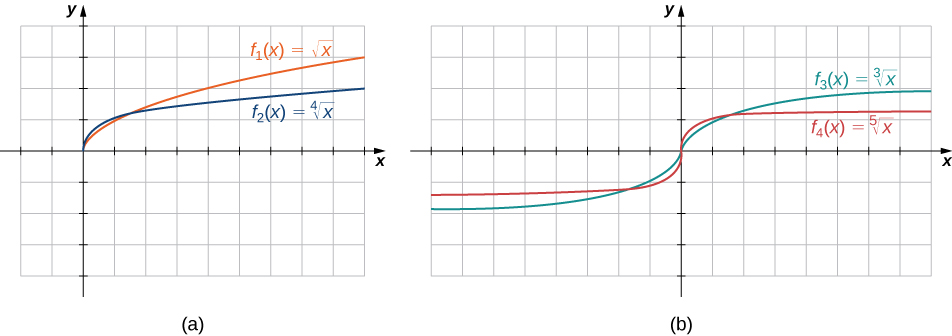
Kazi za mizizi\(f(x)=x^{1/n}\) zina sifa zinazofafanua kulingana na ikiwa\(n\) ni isiyo ya kawaida au hata. Kwa wote hata integers\(n≥2\), uwanja wa\(f(x)=x^{1/n}\) ni muda\([0,∞)\). Kwa integers zote isiyo ya kawaida\(n≥1\), uwanja wa\(f(x)=x^{1/n}\) ni seti ya namba zote halisi. Tangu\(x^{1/n}=(−x)^{1/n}\) kwa integers isiyo ya kawaida\(n\),\(f(x)=x^{1/n}\) ni kazi isiyo ya kawaida kama\(n\) ni isiyo ya kawaida. Angalia grafu ya kazi mizizi kwa maadili tofauti ya\(n\) katika Kielelezo\(\PageIndex{7}\).
Kwa kila kazi zifuatazo, tambua uwanja wa kazi.
- \(f(x)=\dfrac{3}{x^2−1}\)
- \(f(x)=\dfrac{2x+5}{3x^2+4}\)
- \(f(x)=\sqrt{4−3x}\)
- \(f(x)=\sqrt[3]{2x−1}\)
Suluhisho
- Huwezi kugawanya kwa sifuri, hivyo uwanja ni seti ya maadili\(x\) kama hayo\(x^2−1≠0\). Kwa hiyo, uwanja ni\(\{x\,|\,x≠±1\}\).
- Unahitaji kuamua maadili ambayo\(x\) denominator ni sifuri. Tangu\(3x^2+4≥4\) kwa idadi zote halisi\(x\), denominator kamwe sifuri. Kwa hiyo, uwanja ni\((−∞,∞).\)
- Kwa kuwa mizizi ya mraba ya nambari hasi sio namba halisi, uwanja ni seti\(x\) ya maadili ambayo\(4−3x≥0\). Kwa hiyo, uwanja ni\(\{x\,|\,x≤4/3\}.\)
- Mzizi wa mchemraba hufafanuliwa kwa namba zote halisi, hivyo uwanja ni muda\((−∞, ∞).\)
Kupata uwanja kwa kila moja ya kazi zifuatazo:\(f(x)=(5−2x)/(x^2+2)\) na\(g(x)=\sqrt{5x−1}\).
- Kidokezo
-
Kuamua maadili ya\(x\) wakati kujieleza katika denominator ya\(f\) ni nonzero, na kupata maadili ya\(x\) wakati kujieleza ndani ya radical ya\(g\) ni nonnegative.
- Jibu
-
uwanja wa\(f\) ni\((−∞, ∞)\). Uwanja wa\(g\) ni\(\{x\,|\,x≥1/5\}.\)
Kazi Transcendental
Hadi sasa, tumejadili kazi za algebraic. Baadhi ya kazi, hata hivyo, haiwezi kuelezewa na shughuli za msingi za algebraic. Kazi hizi zinajulikana kama kazi za transcendental kwa sababu zinasemekana “kuvuka,” au kwenda zaidi, algebra. Kazi za kawaida za transcendental ni trigonometric, exponential, na logarithmic kazi. Kazi ya trigonometric inahusiana na uwiano wa pande mbili za pembetatu sahihi. Wao ni\(\sin x, \cos x, \tan x, \cot x, \sec x,\text{ and }\csc x.\) (Sisi kujadili kazi trigonometric baadaye katika sura.) Kazi ya kielelezo ni kazi ya fomu\(f(x)=b^x\), ambapo msingi\(b>0,\, b≠1\). Kazi ya logarithmic ni kazi ya fomu\(f(x)=\log_b(x)\) kwa mara kwa mara\(b>0,\,b≠1,\) ambapo\(\log_b(x)=y\) ikiwa na ikiwa tu\(b^y=x\). (Sisi pia kujadili kazi kielelezo na logarithmic baadaye katika sura.)
Weka kila moja ya kazi zifuatazo, a. kupitia c., kama algebraic au transcendental.
- \(f(x)=\dfrac{\sqrt{x^3+1}}{4x+2}\)
- \(f(x)=2^{x^2}\)
- \( f(x)=\sin(2x)\)
Suluhisho
- Kwa kuwa kazi hii inahusisha shughuli za msingi za algebraic tu, ni kazi ya algebraic.
- Kazi hii haiwezi kuandikwa kama formula inayohusisha shughuli za msingi za algebraic tu, hivyo ni transcendental. (Kumbuka kuwa kazi za algebraic zinaweza tu kuwa na nguvu ambazo ni namba za busara.)
- Kama ilivyo katika sehemu ya b, kazi hii haiwezi kuandikwa kwa kutumia formula inayohusisha shughuli za msingi za algebraic tu; kwa hiyo, kazi hii ni transcendental.
Je\(f(x)=x/2\), ni kazi ya algebraic au transcendental?
- Jibu
-
Kialjebra
Kazi zilizoelezwa Kipande
Wakati mwingine kazi inaelezwa na formula tofauti kwenye sehemu tofauti za uwanja wake. kazi na mali hii inajulikana kama kazi piecewise-defined. thamani kamili kazi ni mfano wa kazi piecewise-defined kwa sababu formula mabadiliko na ishara ya\(x\):
\[f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}. \nonumber \]
Kazi nyingine zilizoelezwa kwa kipande zinaweza kuwakilishwa na fomu tofauti kabisa, kulingana na sehemu ya uwanja ambao hatua huanguka. Ili kuchapisha kazi iliyofafanuliwa kwa kipande, tunaweka kila sehemu ya kazi katika uwanja wake, kwenye mfumo huo wa kuratibu. Kama formula kwa ajili ya kazi ni tofauti kwa\(x<a\) na\(x>a\), tunahitaji kulipa kipaumbele maalum kwa nini kinatokea\(x=a\) wakati sisi grafu kazi. Wakati mwingine grafu inahitaji kuingiza mduara wazi au uliofungwa ili kuonyesha thamani ya kazi\(x=a\). Tunachunguza hili katika mfano unaofuata.
Mchoro grafu ya kazi inayofuatia kipande:
\[f(x)=\begin{cases}x+3, & \text{if } x<1\\(x−2)^2, & \text{if } x≥1\end{cases} \nonumber \]
Suluhisho
Graph kazi ya mstari\(y=x+3\) kwenye muda\((−∞,1)\) na grafu kazi\(y=(x−2)^2\) ya quadratic kwa muda\([1,∞)\). Kwa kuwa thamani ya kazi katika\(x=1\) inapewa na formula\(f(x)=(x−2)^2\), tunaona hiyo\(f(1)=1\). Ili kuonyesha hii kwenye grafu, tunapata mduara uliofungwa wakati huo\((1,1)\). Thamani ya kazi hutolewa na\(f(x)=x+3\) kwa wote\(x<1\), lakini sio\(x=1\). Ili kuonyesha hii kwenye grafu, tunapata mduara wazi\((1,4)\).
2) Mchoro grafu ya kazi
\(f(x)=\begin{cases}2−x, & \text{if } x≤2\\x+2, & \text{if } x>2\end{cases}.\)
Suluhisho:
2.Kazi ina x intercept katika (2, 0) na y kukatiza katika (0, 2)." src="https://math.libretexts.org/@api/dek...8509006001.png">
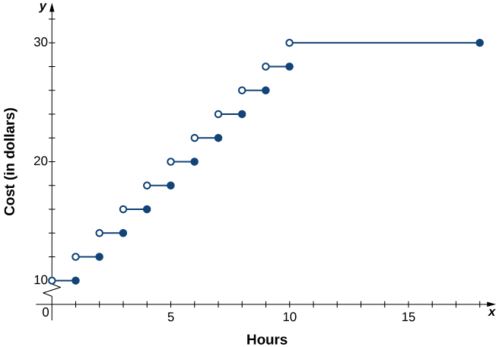
Katika mji mkubwa, madereva wanashtakiwa viwango vya kutofautiana kwa maegesho katika karakana ya maegesho. Wao ni kushtakiwa $10 kwa saa ya kwanza au sehemu yoyote ya saa ya kwanza na ziada $2 kwa kila saa au sehemu yake hadi upeo wa $30 kwa siku. Gereji ya maegesho inafunguliwa kutoka 6:00 hadi usiku wa manane 12.
- Andika kazi piecewise-defined kwamba inaeleza gharama\(C\) ya Hifadhi katika maegesho karakana kama kazi ya masaa parked\(x\).
- Chora grafu ya kazi hii\(C(x).\)
Suluhisho
1.Tangu karakana ya maegesho inafunguliwa masaa 18 kila siku, uwanja wa kazi hii ni\(\{x\,|\,0<x≤18\}\). Gharama ya kuendesha gari kwenye karakana hii ya maegesho inaweza kuelezewa kipande kwa kazi
\[C(x)=\begin{cases}10, & \text{for } 0<x≤1\\12, & \text{for } 1<x≤2\\14, & \text{for } 2<x≤3\\16, & \text{for } 3<x≤4\\ ⋮\\30, & \text{for } 10<x≤18\end{cases}. \nonumber \]
2.Grafu ya kazi ina makundi kadhaa ya mstari wa usawa.
Gharama ya barua pepe ni kazi ya uzito wa barua. Tuseme gharama ya barua pepe ni\(49¢\) kwa ounce ya kwanza na\(21¢\) kwa kila ounce ya ziada. Andika piecewise-defined kazi kuelezea gharama\(C\) kama kazi ya uzito\(x\) kwa\(0<x≤3\), ambapo\(C\) ni kipimo katika senti na\(x\) ni kipimo katika ounces.
- Kidokezo
-
Kazi iliyofafanuliwa kwa kipande ni mara kwa mara kwa vipindi\((0,1],\,(1,2],\,….\)
- Jibu
-
\[C(x)=\begin{cases}49, 0<x≤1\\70, 1<x≤2\\91, 2<x≤3\end{cases} \nonumber \]
Mabadiliko ya Kazi
Tumeona matukio kadhaa ambayo tuna aliongeza, subtracted, au tele constants kuunda tofauti ya kazi rahisi. Katika mfano uliopita, kwa mfano, sisi subtracted 2 kutoka hoja ya kazi ya\(y=x^2\) kupata kazi\(f(x)=(x−2)^2\). Ondoa hii inawakilisha mabadiliko ya kazi vitengo\(y=x^2\) viwili kwa haki. Kuhama, kwa usawa au kwa wima, ni aina ya mabadiliko ya kazi. Mabadiliko mengine yanajumuisha usawa na wima scalings, na tafakari kuhusu axes.
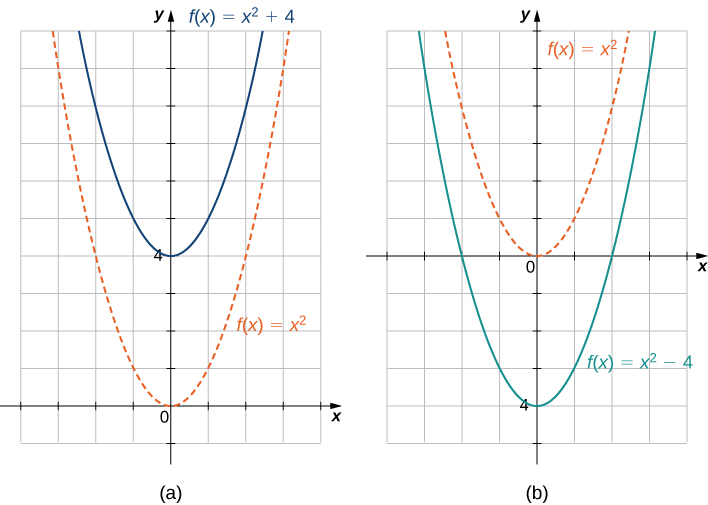
Mabadiliko ya wima ya kazi hutokea ikiwa tunaongeza au kuondoa mara kwa mara sawa kwa kila pato\(y\). Kwa\(c>0\), grafu ya\(f(x)+c\) ni mabadiliko ya grafu ya\(c\) vitengo vya\(f(x)\) juu, wakati grafu ya\(f(x)−c\) ni mabadiliko ya grafu ya\(c\) vitengo vya\(f(x)\) chini. Kwa mfano, grafu ya kazi\(f(x)=x^3+4\) ni grafu ya\(4\) vitengo vya\(y=x^3\) kubadilishwa; grafu ya kazi\(f(x)=x^3−4\) ni grafu ya\(4\) vitengo vya\(y=x^3\) kubadilishwa chini (Kielelezo\(\PageIndex{9}\)).
Mabadiliko ya usawa ya kazi hutokea ikiwa tunaongeza au kuondoa mara kwa mara sawa kwa kila pembejeo\(x\). Kwa\(c>0\), grafu ya\(f(x+c)\) ni mabadiliko ya grafu ya\(f(x)\)\(c\) vitengo vya kushoto; grafu ya\(f(x−c)\) ni mabadiliko ya grafu ya\(f(x)\)\(c\) vitengo vya kulia. Kwa nini grafu inabadilika kushoto wakati wa kuongeza mara kwa mara na kuhama haki wakati wa kuondoa mara kwa mara? Ili kujibu swali hili, hebu tuangalie mfano.
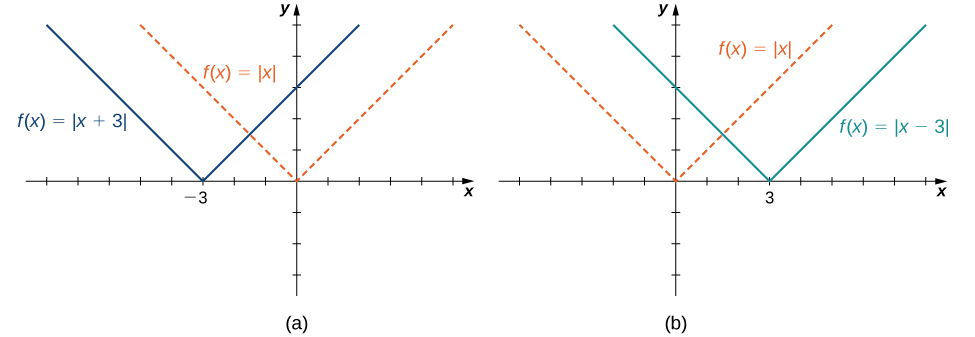
Fikiria kazi\(f(x)=|x+3|\) na tathmini kazi hii\(x−3\). Tangu\(f(x−3)=|x|\) na\(x−3<x\), grafu ya\(f(x)=|x+3|\) ni grafu ya\(3\) vitengo vya kushoto\(y=|x|\) vilivyobadilishwa. Vile vile, grafu ya\(f(x)=|x−3|\) ni grafu ya\(3\) vitengo vya haki\(y=|x|\) vilivyobadilishwa (Kielelezo\(\PageIndex{10}\)).
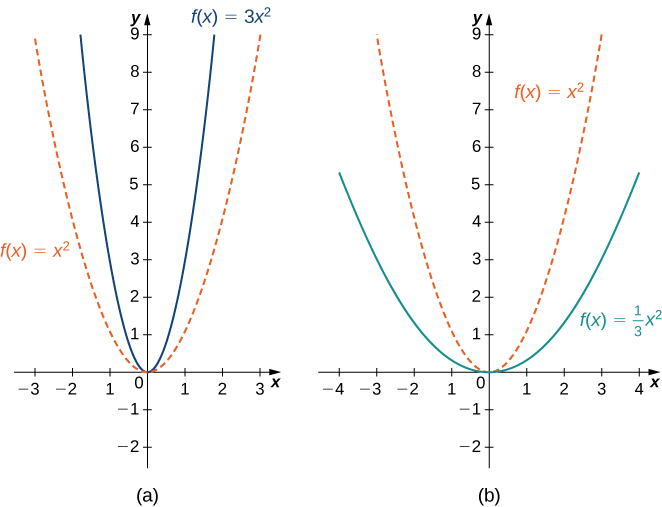
Upeo wa wima wa grafu hutokea ikiwa tunazidisha matokeo yote\(y\) ya kazi kwa mara kwa mara sawa. Kwa\(c>0\), grafu ya kazi\(cf(x)\) ni grafu ya\(f(x)\) kuongezwa kwa wima kwa sababu ya\(c\). Ikiwa\(c>1\), maadili ya matokeo ya kazi\(cf(x)\) ni kubwa zaidi kuliko maadili ya matokeo ya kazi\(f(x)\); kwa hiyo, grafu imetambulishwa kwa wima. Ikiwa\(0<c<1\), basi matokeo ya kazi\(cf(x)\) ni ndogo, hivyo grafu imesisitizwa. Kwa mfano, grafu ya kazi\(f(x)=3x^2\) ni grafu ya\(y=x^2\) kunyoosha kwa wima kwa sababu ya 3, wakati grafu ya\(f(x)=x^2/3\) ni grafu ya\(y=x^2\) kusisitizwa kwa wima kwa sababu ya\(3\) (Kielelezo\(\PageIndex{11b}\)).
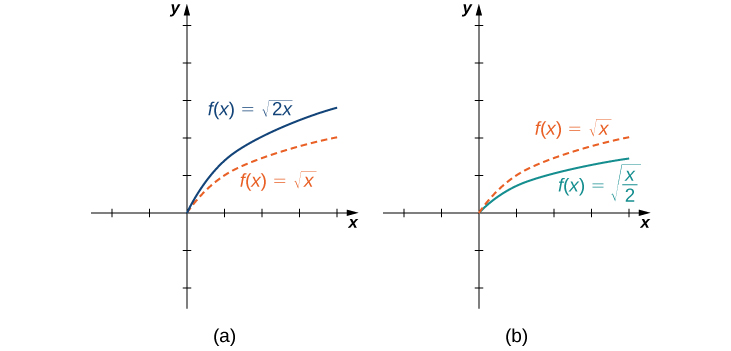
Upeo wa usawa wa kazi hutokea ikiwa tunazidisha pembejeo\(x\) kwa mara kwa mara sawa. Kwa\(c>0\), grafu ya kazi\(f(cx)\) ni grafu ya\(f(x)\) kuongezwa kwa usawa kwa sababu ya\(c\). Ikiwa\(c>1\), grafu ya\(f(cx)\) ni grafu ya\(f(x)\) kusisitizwa kwa usawa. Ikiwa\(0<c<1\), grafu ya\(f(cx)\) ni grafu ya\(f(x)\) kunyoosha kwa usawa. Kwa mfano, fikiria kazi\(f(x)=\sqrt{2x}\) na tathmini\(f\) saa\(x/2\). Tangu\(f(x/2)=\sqrt{x}\), grafu ya\(f(x)=\sqrt{2x}\) ni grafu ya\(y=\sqrt{x}\) USITUMIE usawa. Grafu ya\(y=\sqrt{x/2}\) ni kunyoosha usawa wa grafu ya\(y=\sqrt{x}\) (Kielelezo\(\PageIndex{12}\)).
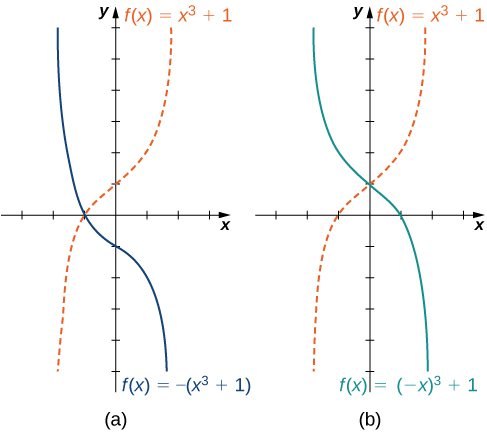
Sisi kuchunguzwa nini kinatokea kwa graph ya kazi\(f\) wakati sisi kuzidisha\(f\) kwa mara\(c>0\) kwa mara kupata kazi mpya\(cf(x)\). Sisi pia kujadili nini kinatokea kwa graph ya kazi\(f\) wakati sisi kuzidisha variable\(x\) huru na kupata kazi mpya\(f(cx)\).\(c>0\) Hata hivyo, hatujashughulikia kile kinachotokea kwenye grafu ya kazi ikiwa mara kwa mara\(c\) ni hasi. Kama tuna mara kwa mara\(c<0\), tunaweza kuandika\(c\) kama idadi chanya kuzidisha kwa\(−1\); lakini, ni aina gani ya mabadiliko sisi kupata wakati sisi kuzidisha kazi au hoja yake na\(−1?\) Wakati sisi kuzidisha matokeo yote kwa\(−1\), sisi kupata reflection kuhusu\(x\) -axis. Wakati sisi kuzidisha pembejeo zote na\(−1\), sisi kupata reflection kuhusu\(y\) -axis. Kwa mfano, grafu ya\(f(x)=−(x^3+1)\) ni grafu ya\(y=(x^3+1)\) yalijitokeza kuhusu\(x\) -axis. Grafu ya\(f(x)=(−x)^3+1\) ni grafu ya\(y=x^3+1\) yalijitokeza kuhusu\(y\) -axis (Kielelezo\(\PageIndex{13}\)).
Ikiwa grafu ya kazi ina mabadiliko zaidi ya moja ya grafu nyingine, ni muhimu kubadilisha grafu kwa utaratibu sahihi. Kutokana na kazi\(f(x)\), grafu ya kazi inayohusiana\(y=cf(a(x+b))+d\) inaweza kupatikana kutoka kwenye grafu ya\(y=f(x)\) kwa kufanya mabadiliko kwa utaratibu wafuatayo.
- Horizontal kuhama ya grafu ya\(y=f(x)\). Kama\(b>0\), kuhama kushoto. Kama\(b<0\) kuhama haki.
- Horizontal kuongeza ya grafu ya\(y=f(x+b)\) kwa sababu ya\(|a|\). Ikiwa\(a<0\), tafakari grafu kuhusu\(y\) -axis.
- Upeo wa wima wa grafu ya\(y=f(a(x+b))\) kwa sababu ya\(|c|\). Ikiwa\(c<0\), tafakari grafu kuhusu\(x\) -axis.
- Wima kuhama ya grafu ya\(y=cf(a(x+b))\). Kama\(d>0\), kuhama up. Kama\(d<0\), kuhama chini.
Tunaweza muhtasari mabadiliko mbalimbali na madhara yao kuhusiana na grafu ya kazi katika meza ifuatayo.
| Mabadiliko ya\(f (c>0)\) | Athari ya grafu ya\(f\) |
|---|---|
| \ (f (c>0)\)” style="text-align:katikati; wima align:katikati; ">\(f(x)+c\) | \ (f\)” style="text-align:katikati; wima align:katikati; "> Vipande\(c\) vya kugeuza wima |
| \ (f (c>0)\)” style="text-align:katikati; wima align:katikati; ">\(f(x)-c\) | \ (f\)” style="text-align:center; wima align:katikati; "> Kubadilisha wima chini\(c\) vitengo |
| \ (f (c>0)\)” style="text-align:katikati; wima align:katikati; ">\(f(x+c)\) | \ (f\)” style="text-align:katikati; wima align:katikati; "> Shift kushoto na\(c\) vitengo |
| \ (f (c>0)\)” style="text-align:katikati; wima align:katikati; ">\(f(x-c)\) | \ (f\)” style="text-align:katikati; wima align:katikati; "> Shift kulia kwa\(c\) vitengo |
| \ (f (c>0)\)” style="text-align:katikati; wima align:katikati; ">\(cf(x)\) | \ (f\)” style="wima align:katikati; ">
Kuweka wima ikiwa\(c>1\); compression wima kama\(0<c<1\) |
| \ (f (c>0)\)” style="text-align:katikati; wima align:katikati; ">\(f(cx)\) | \ (f\)” style="wima align:katikati; ">
Kunyoosha usawa ikiwa\(0<c<1\); compression usawa kama\(c>1\) |
| \ (f (c>0)\)” style="text-align:katikati; wima align:katikati; ">\(-f(x)\) | \ (f\)” style="text-align:center; wima align:katikati; "> Tafakari kuhusu\(x\) -axis |
| \ (f (c>0)\)” style="text-align:katikati; wima align:katikati; ">\(f(-x)\) | \ (f\)” style="text-align:center; wima align:katikati; "> Tafakari kuhusu\(y\) -axis |
Kwa kila moja ya kazi zifuatazo, a. na b., mchoro grafu kwa kutumia mlolongo wa mabadiliko ya kazi inayojulikana.
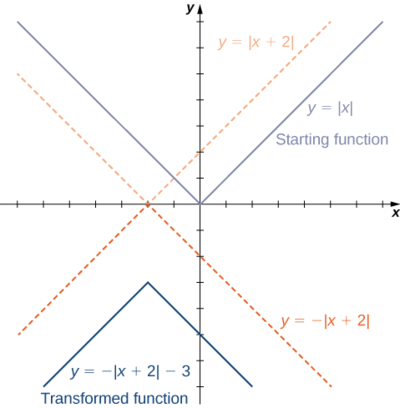
- \(f(x)=−|x+2|−3\)
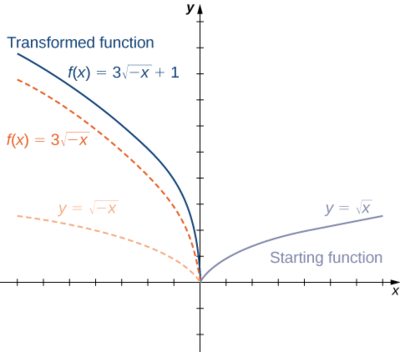
- \(f(x)=\sqrt[3]{x}+1\)
Suluhisho
1.Kuanzia na grafu ya\(y=|x|\), kuhama\(2\) vitengo upande wa kushoto, kutafakari kuhusu\(x\) -axis, na kisha kuhama chini\(3\) vitengo.
2. Kuanzia na grafu ya\(y=sqrt{x},\) kutafakari juu ya\(y\) -axis, weka grafu kwa wima kwa sababu ya 3, na uendelee kitengo 1.
Eleza jinsi kazi\(f(x)=−(x+1)^2−4\) inaweza kuwa graphed kwa kutumia grafu ya\(y=x^2\) na mlolongo wa mabadiliko
- Jibu
-
Shift grafu\(y=x^2\) kwenye kitengo cha kushoto cha 1, kutafakari juu ya\(x\) -axis, kisha ugeuke chini vitengo 4.
Dhana muhimu
- kazi nguvu\(f(x)=x^n\) ni hata kazi kama n ni hata na\(n≠0\), na ni kazi isiyo ya kawaida kama\(n\) ni isiyo ya kawaida.
- Kazi ya mizizi\(f(x)=x^{1/n}\) ina kikoa\([0,∞)\) ikiwa n ni hata na kikoa\((−∞,∞)\) ikiwa\(n\) ni isiyo ya kawaida. Kama\(n\) ni isiyo ya kawaida, basi\(f(x)=x^{1/n}\) ni kazi isiyo ya kawaida.
- Kikoa cha kazi ya busara\(f(x)=p(x)/q(x)\), wapi\(p(x)\) na\(q(x)\) ni kazi nyingi, ni seti ya\(x\) vile\(q(x)≠0\).
- Kazi zinazohusisha shughuli za msingi za kuongeza, kuondoa, kuzidisha, mgawanyiko, na nguvu ni kazi za algebraic. Kazi nyingine zote ni transcendental. Kazi za trigonometric, kielelezo, na logarithmic ni mifano ya kazi za transcendental.
- kazi polynomial\(f\) na shahada\(n≥1\) satisfies\(f(x)→±∞\) kama\(x→±∞\). Ishara ya pato\(x→∞\) inategemea ishara ya mgawo wa kuongoza tu na ikiwa\(n\) ni hata au isiyo ya kawaida.
- Mabadiliko ya wima na ya usawa, scalings wima na usawa, na kutafakari juu ya\(x\) - na\(y\) -axes ni mifano ya mabadiliko ya kazi.
Mlinganyo muhimu
- Equation ya mteremko wa mstari\[y−y_1=m(x−x_1)\nonumber \]
- Aina ya kupinga mteremko wa mstari\[y=mx+b\nonumber \]
- Aina ya kawaida ya mstari\[ax+by=c\nonumber \]
- Kazi ya polynomial\[f(x)=a_n{x^n}+a_{n−1}x^{n−1}+⋯+a_1x+a_0\nonumber \]
faharasa
- kazi ya aljebra
- kazi kuwashirikisha mchanganyiko wowote wa shughuli za msingi tu ya kuongeza, kutoa, kuzidisha, mgawanyiko, nguvu, na mizizi kutumika kwa variable pembejeo\(x\)
- kazi za ujazo
- polynomial ya shahada ya 3; yaani, kazi ya fomu\(f(x)=ax^3+bx^2+cx+d\), ambapo\(a≠0\)
- shahada
- kwa ajili ya kazi polynomial, thamani ya exponent kubwa ya muda wowote
- kazi ya mstari
- kazi ambayo inaweza kuandikwa kwa fomu\(f(x)=mx+b\)
- kazi ya logarithmic
- kazi ya fomu\(f(x)=\log_b(x)\) kwa baadhi ya msingi\(b>0,\,b≠1\) vile kwamba\(y=\log_b(x)\) kama na tu kama\(b^y=x\)
- mfano wa hisabati
- Njia ya kuiga hali halisi ya maisha na milinganyo ya hisabati
- kazi iliyofafanuliwa kipande
- kazi inayofafanuliwa tofauti kwenye sehemu tofauti za kikoa chake
- equation ya mteremko
- equation ya kazi linear kuonyesha mteremko wake na uhakika juu ya grafu ya kazi
- kazi ya polynomial
- kazi ya fomu\(f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0\)
- kazi ya nguvu
- kazi ya fomu\(f(x)=x^n\) kwa integer yoyote nzuri\(n≥1\)
- kazi ya quadratic
- polynomial ya shahada ya 2; yaani, kazi ya fomu\(f(x)=ax^2+bx+c\) ambapo\(a≠0\)
- kazi ya busara
- kazi ya fomu\(f(x)=p(x)/q(x)\), wapi\(p(x)\) na\(q(x)\) ni polynomials
- kazi ya mizizi
- kazi ya fomu\(f(x)=x^{1/n}\) kwa integer yoyote\(n≥2\)
- mteremko
- mabadiliko katika mabadiliko\(y\) ya kila kitengo\(x\)
- fomu ya kupinga mteremko
- equation ya kazi linear kuonyesha mteremko wake na\(y\) -intercept
- kazi transcendental
- kazi ambayo haiwezi kuonyeshwa kwa mchanganyiko wa shughuli za msingi za hesabu
- mabadiliko ya kazi
- mabadiliko, kuongeza, au kutafakari kazi


