13.5: Kanuni za Kuhesabu
- Page ID
- 177882
- Tatua matatizo ya kuhesabu kwa kutumia Kanuni ya Kuongeza.
- Tatua matatizo ya kuhesabu kwa kutumia Kanuni ya Kuzidisha.
- Kutatua matatizo kuhesabu kwa kutumia vibali kuwashirikisha n vitu tofauti.
- Tatua matatizo ya kuhesabu kwa kutumia mchanganyiko.
- Pata idadi ya subsets ya seti iliyotolewa.
- Kutatua matatizo kuhesabu kwa kutumia vibali kuwashirikisha n vitu zisizo tofauti.
Kampuni mpya inauza kesi za customizable kwa vidonge na simu za mkononi. Kila kesi inakuja katika rangi mbalimbali na inaweza kuwa ya kibinafsi kwa ada ya ziada na picha au monogram. Mteja anaweza kuchagua kutobinafsisha au anaweza kuchagua kuwa na picha moja, mbili, au tatu au monogram. Mteja anaweza kuchagua utaratibu wa picha na barua katika monogram. Kampuni hiyo inafanya kazi na shirika la kuendeleza kampeni ya masoko kwa kuzingatia idadi kubwa ya chaguzi wanazotoa. Kuhesabu uwezekano ni changamoto!
Tunakutana na matatizo mbalimbali ya kuhesabu kila siku. Kuna tawi la hisabati linalojitolea kwa utafiti wa matatizo ya kuhesabu kama hii. Matumizi mengine ya kuhesabu ni pamoja na nywila salama, matokeo ya racing farasi, na uchaguzi wa ratiba ya chuo. Tutachunguza aina hii ya hisabati katika sehemu hii.
Kutumia Kanuni ya Kuongeza
Kampuni inayouza kesi za customizable hutoa kesi kwa vidonge na simu za mkononi. Kuna mifano ya kibao\(3\) iliyoungwa mkono na mifano ya smartphone\(5\) iliyoungwa mkono. Kanuni ya Kuongeza inatuambia kwamba tunaweza kuongeza idadi ya chaguzi za kibao kwa idadi ya chaguzi za smartphone ili kupata idadi ya chaguzi. Kwa Kanuni ya Kuongeza, kuna chaguzi za\(8\) jumla, kama tunavyoweza kuona kwenye Kielelezo\(\PageIndex{1}\).
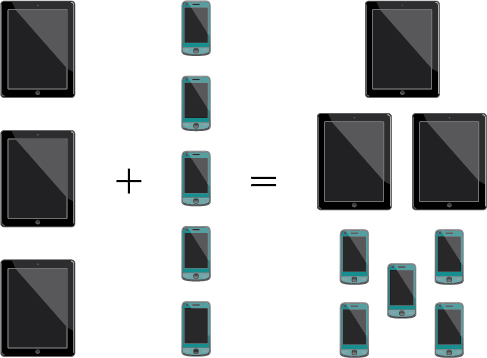
Kielelezo\(\PageIndex{1}\)
Kwa mujibu wa Kanuni ya Kuongezea, ikiwa tukio moja linaweza kutokea kwa\(m\) njia na tukio la pili bila matokeo ya kawaida yanaweza kutokea kwa\(n\) njia, basi tukio la kwanza au la pili linaweza kutokea kwa\(m+n\) njia.
Kuna\(2\) mboga entrée chaguzi na\(5\) nyama entrée chaguzi katika orodha ya chakula cha jioni. Jumla ya idadi ya chaguzi entrée ni nini?
Suluhisho
Tunaweza kuongeza idadi ya chaguzi mboga na idadi ya chaguzi nyama ili kupata idadi ya chaguzi entrée.

Kuna chaguzi\(7\) jumla.
Mwanafunzi ni ununuzi kwa kompyuta mpya. Anaamua kati ya\(3\) kompyuta za kompyuta na\(4\) kompyuta za kompyuta. Idadi ya chaguzi za kompyuta ni nini?
- Jibu
-
\(7\)
Kutumia Kanuni ya Kuzidisha
Kanuni ya Kuzidisha inatumika wakati tunapofanya uteuzi zaidi ya moja. Tuseme sisi ni kuchagua appetizer, entrée, na dessert. Kama kuna\(2\) appetizer chaguzi, chaguzi\(3\) entrée, na chaguzi\(2\) dessert juu ya fasta bei chakula cha jioni menu, kuna jumla ya uchaguzi\(12\) inawezekana ya kila mmoja kama inavyoonekana katika mchoro mti katika Kielelezo\(\PageIndex{2}\).
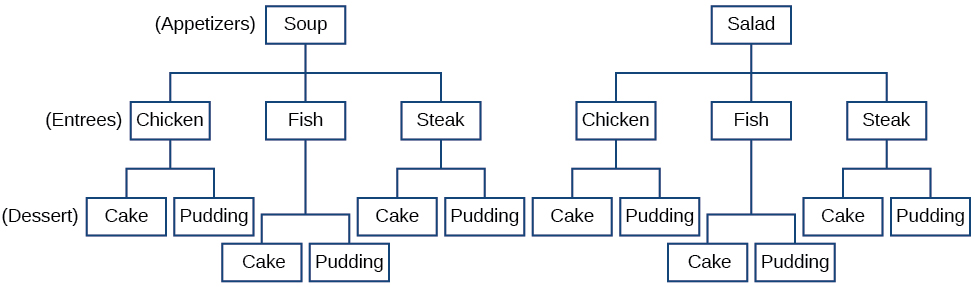
Kielelezo\(\PageIndex{2}\)
Uchaguzi unaowezekana ni:
- supu, kuku, keki
- supu, kuku, pudding
- supu, samaki, keki
- supu, samaki, pudding
- supu, steak, keki
- supu, steak, pudding
- saladi, kuku, keki
- saladi, kuku, pudding
- saladi, samaki, keki
- saladi, samaki, pudding
- saladi, steak, keki
- saladi, steak, pudding Tunaweza pia kupata idadi ya dinners iwezekanavyo kwa kuzidisha.
Tunaweza pia kuhitimisha kwamba kuna\(12\) uwezekano wa chakula cha jioni uchaguzi tu kwa kutumia Kanuni ya Kuzidisha.
\(\# \text{of appetizer options} \times \# \text {of entree options} \times \# \text {of dessert options}\)
\(2 × 3 × 2=12\)
Kwa mujibu wa Kanuni ya Kuzidisha, ikiwa tukio moja linaweza kutokea kwa\(m\) njia na tukio la pili linaweza kutokea kwa\(n\) njia baada ya tukio la kwanza limetokea, basi matukio hayo mawili yanaweza kutokea kwa\(m×n\) njia. Hii pia inajulikana kama Kanuni ya Kuhesabu Msingi.
Diane packed\(2\) sketi,\(4\) blauzi, na sweta kwa ajili ya safari yake ya biashara. Atahitaji kuchagua skirt na blouse kwa kila outfit na kuamua kama kuvaa sweta. Tumia Kanuni ya Kuzidisha ili kupata idadi ya mavazi iwezekanavyo.
Suluhisho
Ili kupata idadi ya mavazi, pata bidhaa ya idadi ya chaguzi za skirt, idadi ya chaguzi za blouse, na idadi ya chaguzi za jasho.

Kuna mavazi\(16\) iwezekanavyo.
Mgahawa hutoa kifungua kinywa maalum ambacho kinajumuisha sandwich ya kifungua kinywa, sahani ya upande, na kinywaji. Kuna\(3\) aina ya sandwiches kifungua kinywa, chaguzi\(4\) upande sahani, na uchaguzi\(5\) kinywaji. Kupata idadi ya Specials iwezekanavyo kifungua kinywa.
- Jibu
-
Kuna\(60\) iwezekanavyo kifungua kinywa Specials.
Kutafuta Idadi ya vibali vya vitu\(n\) tofauti
Kanuni ya Kuzidisha inaweza kutumika kutatua aina mbalimbali za tatizo. Aina moja ya tatizo inahusisha kuweka vitu kwa utaratibu. Tunapanga barua kwa maneno na tarakimu kwa namba, mstari wa picha, kupamba vyumba, na zaidi. Uagizaji wa vitu huitwa ruhusa.
Kutafuta Idadi ya vibali vya vitu\(n\) tofauti Kutumia Kanuni ya Kuzidisha
Ili kutatua matatizo ya vibali, mara nyingi husaidia kuteka makundi ya mstari kwa kila chaguo. Hiyo inatuwezesha kuamua idadi ya kila chaguo ili tuweze kuzidisha. Kwa mfano, tuseme tuna uchoraji nne, na tunataka kupata idadi ya njia tunaweza hutegemea tatu ya uchoraji ili juu ya ukuta. Tunaweza kuteka mistari mitatu ili kuwakilisha maeneo matatu kwenye ukuta.

Kuna chaguzi nne kwa nafasi ya kwanza, hivyo tunaandika\(4\) kwenye mstari wa kwanza.

Baada ya nafasi ya kwanza imejazwa, kuna chaguzi tatu kwa nafasi ya pili kwa hiyo tunaandika\(3\) kwenye mstari wa pili.
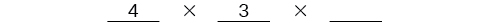
Baada ya nafasi ya pili imejazwa, kuna chaguzi mbili kwa nafasi ya tatu kwa hiyo tunaandika\(2\) kwenye mstari wa tatu. Hatimaye, tunapata bidhaa.
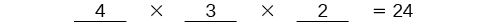
Kuna vibali\(24\) vinavyowezekana vya uchoraji.
- Kuamua ni chaguo ngapi zilizopo kwa hali ya kwanza.
- Kuamua ni chaguo ngapi zilizoachwa kwa hali ya pili.
- Endelea mpaka matangazo yote yamejaa.
- Kuzidisha idadi pamoja.
Katika mashindano ya kuogelea, waogeleaji tisa wanashindana katika mbio.
- Ni njia ngapi ambazo zinaweza kuweka kwanza, ya pili, na ya tatu?
- Ni njia ngapi ambazo zinaweza kuweka kwanza, ya pili, na ya tatu ikiwa mwogeleaji aitwaye Ariel atashinda nafasi ya kwanza? (Kudhani kuna mgombea mmoja tu aitwaye Ariel.)
- Ni njia ngapi ambazo waogeleaji wote tisa wanaweza kuinua picha?
Suluhisho
- Chora mistari kwa kila mahali.

Kuna\(9\) chaguzi kwa nafasi ya kwanza. Mara baada ya mtu kushinda nafasi ya kwanza, kuna chaguzi\(8\) zilizobaki kwa nafasi ya pili. Mara baada ya nafasi ya kwanza na ya pili imeshinda, kuna chaguzi\(7\) zilizobaki kwa nafasi ya tatu.
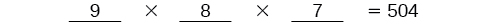
Kuzidisha ili kupata kwamba kuna\(504\) njia za waogeleaji kuweka.
- Chora mistari ya kuelezea kila mahali.
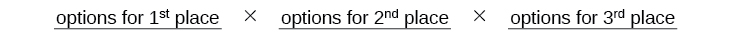
Tunajua Ariel lazima kushinda nafasi ya kwanza, hivyo kuna\(1\) chaguo tu kwa nafasi ya kwanza. Kuna chaguzi\(8\) zilizobaki kwa nafasi ya pili, na kisha chaguo\(7\) zilizobaki kwa nafasi ya tatu.
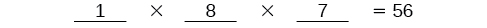
Kuzidisha ili kupata kwamba kuna\(56\) njia za waogeleaji kuweka kama Ariel atashinda kwanza.
- Chora mistari ya kuelezea kila mahali kwenye picha.

Kuna\(9\) uchaguzi kwa doa ya kwanza, kisha\(8\) kwa pili,\(7\) kwa tatu,\(6\) kwa nne, na kadhalika mpaka\(1\) mtu pekee atakaa kwa doa ya mwisho.
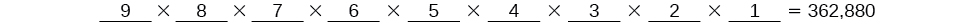
Kuna vibali\(362,880\) vinavyowezekana kwa waogeleaji kuinua.
Uchambuzi
Kumbuka kuwa katika sehemu c, tuligundua kulikuwa na\(9!\) njia za\(9\) watu kuelekea. Idadi ya vibali vya vitu\(n\) tofauti vinaweza kupatikana kila wakati\(n!\).
familia ya tano ni kuwa na portraits kuchukuliwa. Tumia Kanuni ya Kuzidisha ili kupata zifuatazo:
- Ni njia ngapi ambazo familia zinaweza kuunganisha picha?
- Ni njia ngapi ambazo mpiga picha anaweza kuunganisha wanachama wa\(3\) familia?
- Ni njia ngapi ambazo familia zinaweza kuunganisha picha ikiwa wazazi wanatakiwa kusimama kila mwisho?
- Jibu
-
\(120\)
- Jibu b
-
\(60\)
- Jibu c
-
\(12\)
Kupata Idadi ya Permutations ya n Vitu tofauti Kutumia Mfumo
Kwa baadhi ya matatizo ya vibali, ni vigumu kutumia Kanuni ya Kuzidisha kwa sababu kuna idadi nyingi za kuzidisha. Kwa bahati nzuri, tunaweza kutatua matatizo haya kwa kutumia formula. Kabla ya kujifunza formula, hebu tuangalie maelezo mawili ya kawaida ya vibali. Kama tuna seti ya\(n\) vitu na tunataka kuchagua\(r\) vitu kutoka kuweka ili, sisi kuandika\(P(n,r)\). Njia nyingine ya kuandika hii ni\(nP_r\), notation kawaida kuonekana kwenye kompyuta na calculators. Ili kuhesabu\(P(n,r)\), tunaanza kwa kutafuta\(n!\), idadi ya njia za kuunganisha vitu vyote vya nn. Sisi kisha\((n−r)!\) kugawanya na kufuta\((n−r)\) vitu kwamba hatutaki line up.
Hebu tuone jinsi hii inafanya kazi kwa mfano rahisi. Fikiria klabu ya watu sita. Wanahitaji kumchagua rais, makamu wa rais, na mweka hazina. Watu sita wanaweza kuchaguliwa kuwa rais, yeyote kati ya watu watano waliobaki anaweza kuchaguliwa kuwa makamu wa rais, na yeyote kati ya watu wanne waliobaki anaweza kuchaguliwa kuwa mweka hazina. Idadi ya njia hii inaweza kufanyika ni\(6×5×4=120\). Kutumia factorials, tunapata matokeo sawa.
\(\dfrac{6!}{3!}=\dfrac{6·5·4·3!}{3!}=6·5·4=120 \)
Kuna\(120\) njia za kuchagua\(3\) maafisa ili kutoka klabu na\(6\) wanachama. Tunarejelea hili kama ruhusa ya\(6\) kuchukuliwa kwa\(3\) wakati mmoja. Fomu ya jumla ni kama ifuatavyo.
\[P(n,r)=\dfrac{n!}{(n−r)!}\]
Kumbuka kwamba formula bado inafanya kazi ikiwa tunachagua\(n\) vitu vyote na kuziweka kwa utaratibu. Katika hali hiyo tutakuwa kugawa na\((n−n)!\) au\(0!\), ambayo sisi alisema mapema ni sawa na\(1\). Hivyo idadi ya vibali vya\(n\) vitu vilivyochukuliwa kwa\(n\) wakati ni\(\dfrac{n!}{1}\) au tu\(n!\).
Kutokana na vitu\(n\) tofauti, idadi ya njia za kuchagua\(r\) vitu kutoka kwa kuweka ili ni
\[P(n,r)=\dfrac{n!}{(n−r)!}\]
- Tambua\(n\) kutoka kwa taarifa iliyotolewa.
- Tambua\(r\) kutoka kwa taarifa iliyotolewa.
- Badilisha nafasi\(n\) na\(r\) katika formula na maadili yaliyotolewa.
- Tathmini.
Profesa anaunda mtihani wa\(9\) maswali kutoka benki ya mtihani wa\(12\) maswali. Ni njia ngapi ambazo anaweza kuchagua na kupanga maswali?
Suluhisho
Mbadala\(n=12\) na\(r=9\) katika formula ya vibali na kurahisisha.
\[\begin{align*} P(n,r)&=\dfrac{n!}{(n-r)!}\\ P(12,9)&=\dfrac{12!}{(12-9)!}\\ &=\dfrac{12!}{3!}\\ &=79,833,600 \end{align*}\]
Kuna vibali\(79,833,600\) vinavyowezekana vya maswali ya mtihani!
Uchambuzi
Tunaweza pia kutumia calculator kupata vibali. Kwa tatizo hili, tungeingia\(12\), bonyeza\(nP_r\) kazi, ingiza\(9\), na kisha bonyeza ishara sawa. \(nP_r\)Kazi inaweza kuwa chini ya orodha ya MATH na amri za uwezekano.
Je, tunaweza kutatuliwa mfano hapo juu kwa kutumia Kanuni ya Kuzidisha?
Ndiyo. Tungeweza\(15⋅14⋅13⋅12⋅11⋅10⋅9⋅8⋅7⋅6⋅5⋅4\) kuzidisha ili kupata jibu sawa.
kucheza ina kutupwa ya\(7\) watendaji kuandaa kufanya pazia yao wito. Tumia formula ya vibali ili kupata zifuatazo.
Ni njia ngapi ambazo\(7\) watendaji wanaweza kuinua?
- Jibu
-
\(P(7,7)=5,040\)
Ni njia ngapi\(5\) za\(7\) watendaji zinaweza kuchaguliwa ili kuinua?
- Jibu
-
\(P(7,5)=2,520\)
Pata Idadi ya Mchanganyiko Kutumia Mfumo
Hadi sasa, tumeangalia matatizo ya kutuuliza kuweka vitu kwa utaratibu. Kuna matatizo mengi ambayo tunataka kuchagua vitu vichache kutoka kwa kikundi cha vitu, lakini hatujali kuhusu utaratibu. Wakati sisi ni kuchagua vitu na utaratibu haijalishi, sisi ni kushughulika na mchanganyiko. uteuzi wa\(r\) vitu kutoka seti ya\(n\) vitu ambapo ili haijalishi inaweza kuandikwa kama\(C(n,r)\). Kama vile kwa vibali, pia\(C(n,r)\) inaweza kuandikwa kama\(nC_r\). Katika kesi hii, formula ya jumla ni kama ifuatavyo.
\[C(n,r)=\dfrac{n!}{r!(n−r)!} \label{combo}\]
Tatizo la awali lilizingatiwa kuchagua\(3\) uchoraji\(4\) iwezekanavyo ili kunyongwa kwenye ukuta. Tuligundua kwamba kulikuwa na\(24\) njia\(3\) za kuchagua\(4\) uchoraji kwa utaratibu. Lakini vipi ikiwa hatujali kuhusu utaratibu? Tunataka kutarajia idadi ndogo kwa sababu kuchagua uchoraji\(1, 2, 3\) itakuwa sawa na kuchagua uchoraji\(2, 3, 1\). Ili kupata idadi ya njia\(3\) za kuchagua\(4\) uchoraji, kupuuza utaratibu wa uchoraji, ugawanye idadi ya vibali kwa idadi ya njia za kuagiza\(3\) uchoraji. Kuna\(3!=3·2·1=6\) njia za kuagiza\(3\) uchoraji. Kuna\(\dfrac{24}{6}\), au\(4\) njia\(3\) za kuchagua\(4\) uchoraji. Nambari hii ina maana kwa sababu kila wakati tunapochagua\(3\) uchoraji, hatuwezi kuchagua\(1\) uchoraji. Kuna\(4\) uchoraji tunaweza kuchagua kuchagua, kwa hiyo kuna\(4\) njia\(3\) za kuchagua\(4\) uchoraji.
Kutokana na vitu\(n\) tofauti, idadi ya njia za kuchagua\(r\) vitu kutoka kwenye seti ni
\[C(n,r)=\dfrac{n!}{r!(n−r)!}\]
- Tambua\(n\) kutoka kwa taarifa iliyotolewa.
- Tambua\(r\) kutoka kwa taarifa iliyotolewa.
- Badilisha nafasi\(n\) na\(r\) katika formula na maadili yaliyotolewa.
- Tathmini.
Mgahawa wa chakula cha haraka hutoa chaguzi tano za sahani za upande. Mlo wako unakuja na sahani mbili za upande.
- Ni njia ngapi ambazo unaweza kuchagua sahani zako za upande?
- Ni njia ngapi ambazo unaweza kuchagua sahani za\(3\) upande?
Suluhisho
- Tunataka kuchagua sahani za\(2\) upande kutoka kwa\(5\) chaguo.
\(C(5,2)=\dfrac{5!}{2!(5−2)!}=10\)
- Tunataka kuchagua sahani za\(3\) upande kutoka kwa\(5\) chaguo.
\(C(5,3)=\dfrac{5!}{3!(5−3)!}=10\)
Uchambuzi
Tunaweza pia kutumia calculator graphing kupata mchanganyiko. Ingiza 5, kisha waandishi wa habari\(nC_r\), ingiza 3, na kisha ubofye ishara sawa. The\(nC_r\), kazi inaweza kuwa iko chini ya orodha MATH na amri uwezekano.
Je, ni bahati mbaya kwamba sehemu (a) na (b) katika mfano hapo juu zina majibu sawa?
Hapana. Wakati sisi kuchagua r vitu kutoka vitu n, sisi si kuchagua\((n–r)\) vitu. Kwa hiyo,\(C(n,r)=C(n,n–r)\).
Duka la ice cream hutoa\(10\) ladha ya ice cream. Kuna njia ngapi za kuchagua\(3\) ladha kwa mgawanyiko wa ndizi?
- Jibu
-
\(C(10,3)=120\)
Kupata Idadi ya Subsets ya Kuweka
Tumeangalia tu matatizo ya macho ambayo tulichagua vitu vyenye rr. Katika matatizo mengine, tunataka kufikiria kuchagua kila idadi iwezekanavyo ya vitu. Fikiria, kwa mfano, mgahawa wa pizza ambao hutoa\(5\) toppings. Idadi yoyote ya toppings inaweza kuamuru. Ni pizzas ngapi tofauti zinawezekana?
Ili kujibu swali hili, tunahitaji kufikiria pizzas na idadi yoyote ya toppings. Kuna\(C(5,0)=1\) njia ya kuagiza pizza bila toppings. Kuna\(C(5,1)=5\) njia za kuagiza pizza na topping moja. Kama sisi kuendelea mchakato huu, sisi kupata
\(C(5,0)+C(5,1)+C(5,2)+C(5,3)+C(5,4)+C(5,5)=32\)
Kuna pizzas\(32\) iwezekanavyo. Matokeo haya ni sawa na\(2^5\).
Sisi ni iliyotolewa na mlolongo wa uchaguzi. Kwa kila moja ya vitu nn tuna uchaguzi mbili: ni pamoja na katika subset au la. Hivyo kwa subset nzima tumefanya uchaguzi nn, kila na chaguzi mbili. Hivyo kuna jumla ya\(2·2·2·…·2\) uwezekano kusababisha subsets, njia yote kutoka subset tupu, ambayo sisi kupata wakati sisi kusema “hapana” kila wakati, kwa kuweka awali yenyewe, ambayo sisi kupata wakati sisi kusema “ndiyo” kila wakati.
Seti iliyo na vitu tofauti ina\(2^n\) subsets.
Mgahawa hutoa siagi, jibini, chives, na sour cream kama toppings kwa viazi Motoni. Kuna njia ngapi tofauti za kuagiza viazi?
Suluhisho
Tunatafuta idadi ya subsets ya kuweka na\(4\) vitu. Badilisha\(n=4\) katika formula.
\[\begin{align*} 2^n&=2^4\\ &=16 \end{align*}\]
Kuna njia\(16\) zinazowezekana za kuagiza viazi.
Bar ya sundae kwenye harusi ina\(6\) toppings ya kuchagua. Idadi yoyote ya toppings inaweza kuchaguliwa. Ni jua ngapi tofauti zinawezekana?
- Jibu
-
\(64\)Jumapili
Kutafuta Idadi ya vibali vya vitu visivyo na tofauti
Tumejifunza vibali ambapo vitu vyote vilivyohusika vilikuwa tofauti. Ni nini kinachotokea ikiwa baadhi ya vitu havijulikani? Kwa mfano, tuseme kuna karatasi ya\(12\) stika. Ikiwa stika zote zilikuwa tofauti, kutakuwa na\(12!\) njia za kuagiza stika. Hata hivyo,\(4\) ya stika ni nyota kufanana, na\(3\) ni miezi kufanana. Kwa sababu vitu vyote si tofauti,\(12!\) vibali vingi tulivyohesabu ni marudio. Fomu ya jumla ya hali hii ni kama ifuatavyo.
\[\dfrac{n!}{r_1!r_2!…r_k!}\]
Katika mfano huu, tunahitaji kugawanya kwa idadi ya njia za kuagiza\(4\) nyota na njia za kuagiza miezi kupata idadi ya vibali vya kipekee vya stika.\(3\) Kuna\(4!\) njia za kuagiza nyota na\(3!\) njia za kuagiza mwezi.
\(\dfrac{12!}{4!3!}=3,326,400\)
Kuna\(3,326,400\) njia za kuagiza karatasi ya stika.
Kama kuna mambo nn katika seti na\(r_1\) ni sawa,\(r_2\) ni sawa,\(r_3\) ni sawa, na kadhalika kupitia\(r_k\), idadi ya permutations inaweza kupatikana kwa
\[\dfrac{n!}{r_1!r_2!…r_k!}\]
Pata idadi ya rearrangements ya barua katika neno DINSTINAL.
Suluhisho
Kuna\(8\) barua. Wote\(I\) na\(T\) ni mara kwa\(2\) mara. Mbadala\(n=8\),\(r_1=2\), na\(r_2=2\) katika formula.
\(\dfrac{8!}{2!2!}=10,080\)
Kuna\(10,080\) mipango.
Pata idadi ya rearrangements ya barua katika neno CARRIER.
- Jibu
-
\(840\)
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na mchanganyiko na vibali.
Mlinganyo muhimu
| idadi ya permutations ya vitu\(n\) tofauti kuchukuliwa kwa\(r\) wakati | \(P(n,r)=\dfrac{n!}{(n−r)!}\) |
| idadi ya mchanganyiko wa vitu\(n\) tofauti kuchukuliwa kwa\(r\) wakati | \(C(n,r)=\dfrac{n!}{r!(n−r)!}\) |
| idadi ya vibali vya vitu\(n\) visivyo tofauti | \(\dfrac{n!}{r1!r2!…rk!}\) |
Key Concepts
- If one event can occur in \(m\) ways and a second event with no common outcomes can occur in \(n\) ways, then the first or second event can occur in \(m+n\) ways. See Example \(\PageIndex{1}\).
- If one event can occur in \(m\) ways and a second event can occur in \(n\) ways after the first event has occurred, then the two events can occur in \(m×n\) ways. See Example \(\PageIndex{2}\).
- A permutation is an ordering of \(n\) objects.
- If we have a set of \(n\) objects and we want to choose \(r\) objects from the set in order, we write \(P(n,r)\).
- Permutation problems can be solved using the Multiplication Principle or the formula for \(P(n,r)\). See Example \(\PageIndex{3}\) and Example \(\PageIndex{4}\).
- A selection of objects where the order does not matter is a combination.
- Given \(n\) distinct objects, the number of ways to select \(r\) objects from the set is \(C(n,r)\) and can be found using a formula. See Example \(\PageIndex{5}\).
- A set containing \(n\) distinct objects has \(2n\) subsets. See Example \(\PageIndex{6}\).
- For counting problems involving non-distinct objects, we need to divide to avoid counting duplicate permutations. See Example \(\PageIndex{7}\).


