13.1: Utaratibu na Nukuu zao

Last updated
Save as PDF

Page ID: 177916

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Andika maneno ya mlolongo unaofafanuliwa na formula iliyo wazi.
Andika maneno ya mlolongo unaofafanuliwa na formula ya kujirudia.
Matumizi factorial notation.

Kampuni ya mchezo wa video inazindua kampeni mpya ya matangazo ya kusisimua. Wanatabiri idadi ya ziara za mtandaoni kwenye tovuti yao, au hits, zitakuwa mara mbili kila siku. Mfano wanaotumia unaonyesha$2$ hupiga siku ya kwanza,$4$ hupiga siku ya pili,$8$ hupiga siku ya tatu, na kadhalika (Jedwali$\PageIndex{1}$).

Jedwali$\PageIndex{1}$
Siku	1	2	3	4	5	...
Hits	2	4	8	16	32	...

Ikiwa mfano wao unaendelea, ngapi hits itakuwa mwishoni mwa mwezi? Ili kujibu swali hili, tutahitaji kwanza kujua jinsi ya kuamua orodha ya namba zilizoandikwa kwa utaratibu maalum. Katika sehemu hii, sisi kuchunguza aina hii ya orodha kuamuru.

Kuandika Masharti ya Mlolongo Imeelezwa na Mfumo wa wazi

Njia moja ya kuelezea orodha iliyoamriwa ya namba ni kama mlolongo. Mlolongo ni kazi ambayo uwanja wake ni subset ya idadi ya kuhesabu. Mlolongo ulioanzishwa na idadi ya hits kwenye tovuti ni

$\{ 2,4,8,16,32,…\}$

ellipsis (...) inaonyesha kwamba mlolongo unaendelea kwa muda usiojulikana. Kila namba katika mlolongo inaitwa neno. Masharti tano ya kwanza ya mlolongo huu ni$2$$4$,$8$,$16$, na$32$.

Kuorodhesha maneno yote kwa mlolongo inaweza kuwa mbaya. Kwa mfano, kutafuta idadi ya hits kwenye tovuti mwishoni mwa mwezi itahitaji kuorodhesha$31$ maneno mengi. Njia bora zaidi ya kuamua muda maalum ni kwa kuandika formula ili kufafanua mlolongo.

Aina moja ya formula ni formula wazi, ambayo inafafanua masharti ya mlolongo kwa kutumia msimamo wao katika mlolongo. Fomula wazi ni muhimu kama tunataka kupata muda maalum wa mlolongo bila kupata masharti yote ya awali. Tunaweza kutumia formula ili kupata neno la nth la mlolongo, ambapo nn ni idadi yoyote nzuri. Katika mfano wetu, kila idadi katika mlolongo ni mara mbili idadi ya awali, hivyo tunaweza kutumia nguvu ya 2 kuandika formula kwa muda nth.

$Mlolongo wa {2, 4, 8, 16, 32,...} walionyesha kwa fomu ya kielelezo (yaani, {2 ^ 1, 2 ^ 2, 2 ^ 3,..., 2 ^ n,...}$

Muda wa kwanza wa mlolongo ni$2^1=2$, muda wa pili ni$2^2=4$, muda wa tatu ni$2^3=8$, na kadhalika. Neno la nth la mlolongo linaweza kupatikana kwa kuongeza 2 hadi nguvu ya nth. Fomu ya wazi ya mlolongo inaitwa na barua ya chini ya kesi$a$$b$,,$c$... na usajili$n$. Fomu ya wazi ya mlolongo huu ni

$a_n=2^n$

Sasa kwa kuwa tuna formula kwa muda nth ya mlolongo, tunaweza kujibu swali vinavyotokana mwanzoni mwa sehemu hii. Tuliulizwa kupata idadi ya hits mwishoni mwa mwezi, ambayo tutachukua kuwa siku 31. Ili kupata idadi ya hits siku ya mwisho ya mwezi, tunahitaji kupata muda wa 31 ^wa mlolongo. Tutabadilisha 31$n$ kwa formula.

\[ \begin{align*} a_{31}=2^{31} \\ [5pt] &=2,147,483,648 \end{align*}\]

Ikiwa mwenendo wa mara mbili unaendelea, kampuni$2,147,483,648$ itapata hits siku ya mwisho ya mwezi. Hiyo ni zaidi ya$2.1$ bilioni hits! Idadi kubwa labda ni isiyo ya kweli kwa sababu haina kuchukua maslahi ya walaji na ushindani katika akaunti. Inafanya, hata hivyo, kutoa kampuni ya mwanzo ambayo kuzingatia maamuzi ya biashara.

Njia nyingine ya kuwakilisha mlolongo ni kwa kutumia meza. Masharti tano ya kwanza ya mlolongo na muda wa nth wa mlolongo huonyeshwa katika Jedwali$\PageIndex{2}$.

**Jedwali$\PageIndex{2}$**
$n$	1	2	3	4	5	$n$
$n^{th}$muda wa mlolongo,$a_n$	2	4	8	16	32	$2^n$

Graphing hutoa uwakilishi Visual ya mlolongo kama seti ya pointi tofauti. Tunaweza kuona kutoka grafu katika Kielelezo$\PageIndex{1}$ kwamba idadi ya hits ni kupanda kwa kiwango kielelezo. Mlolongo huu hasa huunda kazi ya kielelezo.

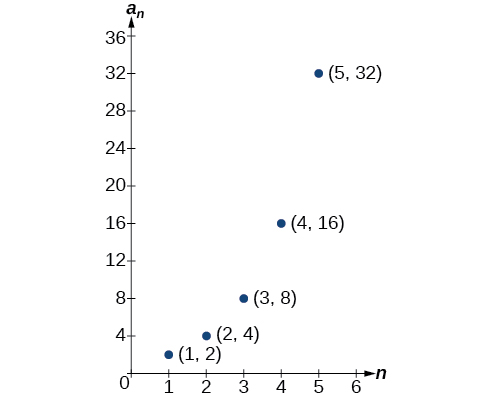
$Grafu ya kazi ya kielelezo iliyopangwa, f (n) = 2 ^ n, ambapo mhimili wa x umeandikwa n na mhimili wa y umeandikwa a_n.$

Kielelezo$\PageIndex{1}$

Mwishowe, tunaweza kuandika mlolongo huu kama

$\{2,4,8,16,32,…,2^n,…\}$

Mlolongo unaoendelea kwa muda usiojulikana huitwa mlolongo usio. Kikoa cha mlolongo usio na kipimo ni seti ya namba za kuhesabu. Ikiwa tunazingatia$10$ masharti ya kwanza ya mlolongo, tunaweza kuandika

$\{2,4,8,16,32,…,2^n,…,1024\}$

Mlolongo huu unaitwa mlolongo wa mwisho kwa sababu hauendelei kwa muda usiojulikana.

MLOLONGO

Mlolongo ni kazi ambayo uwanja wake ni seti ya integers nzuri. Mlolongo wa mwisho ni mlolongo ambao uwanja wake una integers tu ya kwanza$n$ nzuri. Nambari katika mlolongo huitwa maneno. Tofauti$a$ na usajili wa nambari hutumiwa kuwakilisha maneno katika mlolongo na kuonyesha nafasi ya neno katika mlolongo.

\[a_1,a_2,a_3,…,a_n,…\]

Tunaita muda$a_1$ wa kwanza wa mlolongo, muda$a_2$ wa pili wa mlolongo, muda$a_3$ wa tatu wa mlolongo, na kadhalika. Neno$a_n$ linaitwa neno la nth la mlolongo, au muda wa jumla wa mlolongo. Fomu ya wazi inafafanua muda wa nth wa mlolongo kwa kutumia nafasi ya neno. mlolongo kwamba inaendelea kwa muda usiojulikana ni mlolongo usio.

Q & A: Je, mlolongo daima unapaswa kuanza na$a_1$?

Hapana. Katika matatizo fulani, inaweza kuwa na manufaa kufafanua muda wa awali kama$a_0$ badala ya$a_1$. Katika matatizo haya, uwanja wa kazi ni pamoja na$0$.

Jinsi ya: Kutokana na formula wazi, kuandika kwanza$n$ terms of a sequence

Badilisha kila thamani ya$n$ ndani ya formula. Anza na$n=1$ kupata muda wa kwanza,$a_1$.
Ili kupata muda wa pili$a_2$, tumia$n=2$.
Endelea kwa namna ile ile mpaka utakapotambua masharti yote ya nn.

Mfano$\PageIndex{1}$: Writing the Terms of a Sequence Defined by an Explicit Formula

Andika maneno matano ya kwanza ya mlolongo unaofafanuliwa na formula iliyo wazi$a_n=−3n+8$.

Suluhisho

Badala$n=1$ katika formula. Kurudia kwa maadili$2$ kupitia$5$ kwa$n$.

$\begin{array}{ll} n=1 & a_1=−3(1)+8=5 \\ n=2 & a_2=−3(2)+8=2 \\ n=3 & a_3=−3(3)+8=−1 \\ n=4 & a_4=−3(4)+8=−4 \\ n=5 & a_5=−3(5)+8=−7 \end{array}$

Masharti tano ya kwanza ni$\{5,2,−1,−4,−7\}$.

Uchambuzi

Maadili ya mlolongo yanaweza kuorodheshwa kwenye meza. Jedwali, kama Jedwali$\PageIndex{3}$, ni njia rahisi ya kuingiza kazi katika matumizi ya graphing.

Jedwali$\PageIndex{3}$
$n$	1	2	3	4	5
$a_n$	5	2	-1	—4	—7

Grafu inaweza kufanywa kutoka meza hii ya maadili. Kutoka grafu katika Kielelezo$\PageIndex{2}$, tunaweza kuona kwamba mlolongo huu inawakilisha kazi linear, lakini taarifa grafu si kuendelea kwa sababu uwanja ni juu ya integers chanya tu.

$Grafu ya njama iliyotawanyika ambapo x-axis ni lebo n na y-axis ni lebo a_n.$

Kielelezo$\PageIndex{2}$

Zoezi$\PageIndex{1}$

Andika maneno matano ya kwanza ya mlolongo unaofafanuliwa na formula iliyo wazi$t_n=5n−4$.

Jibu: Masharti tano ya kwanza ni$\{1,6, 11, 16, 21\}$.

Kuchunguza Utaratibu mbadala

Wakati mwingine Utaratibu una maneno ambayo ni mbadala. Kwa kweli, maneno inaweza kweli mbadala katika ishara. Hatua za kutafuta maneno ya mlolongo ni sawa na kama ishara hazibadilika. Hata hivyo, maneno yanayotokana hayataonyesha ongezeko au kupungua kama$n$ ongezeko. Hebu tuangalie mlolongo wafuatayo.

$\{2,−4,6,−8\}$

Angalia muda wa kwanza ni mkubwa kuliko muhula wa pili, muda wa pili ni chini ya muhula wa tatu, na muda wa tatu ni mkubwa kuliko muda wa nne. Hali hii inaendelea milele. Usipange upya maneno kwa nambari ili kutafsiri mlolongo.

Jinsi ya: Kutokana na formula wazi na maneno mbadala, kuandika masharti ya kwanza ya nn ya mlolongo

Badilisha kila thamani ya nn katika formula. Anza na$n=1$ kupata muda wa kwanza,$a_1$. Ishara ya neno hutolewa na${(−1)}^n$ fomu iliyo wazi.
Ili kupata muda wa pili$a_2$, tumia$n=2$.
Endelea kwa namna ile ile mpaka utakapotambua$n$ masharti yote.

Mfano$\PageIndex{2}$: Writing the Terms of an Alternating Sequence Defined by an Explicit Formula

Andika maneno matano ya kwanza ya mlolongo.

$a_n=\dfrac{{(−1)}^nn^2}{n+1}$

Suluhisho

Mbadala$n=1$,$n=2$, na kadhalika katika formula.

$\begin{array}{ll} n=1 & a_1=\dfrac{{(−1)}^12^2}{1+1}=−\dfrac{1}{2} \\ n=2 & a_2=\dfrac{{(−1)}^22^2}{2+1}=\dfrac{4}{3} \\ n=3 & a_3=\dfrac{{(−1)}^33^2}{3+1}=−\dfrac{9}{4} \\ n=4 & a_4=\dfrac{{(−1)}^44^2}{4+1}=\dfrac{16}{5} \\ n=5 & a_5=\dfrac{{(−1)}^55^2}{5+1}=−\dfrac{25}{6} \end{array}$

Masharti tano ya kwanza ni$\{−12,43,−94,165,−256\}$.

Uchambuzi

Grafu ya kazi hii, iliyoonyeshwa kwenye Kielelezo$\PageIndex{3}$, inaonekana tofauti na yale tuliyoyaona hapo awali katika sehemu hii kwa sababu maneno ya mlolongo hubadilisha kati ya maadili mazuri na hasi.

$Grafu ya njama iliyotawanyika na pointi zilizoandikwa: (1, -1/2), (2, 4/3), (3, -9/4), (4, 16/5), na (5, -25/6). Mhimili wa x umeandikwa n na mhimili wa y umeandikwa a_n.$

Kielelezo$\PageIndex{3}$

Q & A: Katika mfano hapo juu, je$(–1)$ to the power of $n$ account for the oscillations of signs?

Ndiyo, nguvu inaweza kuwa$n$,$n+1$$n−1$, na kadhalika, lakini mamlaka yoyote isiyo ya kawaida yatasababisha muda usiofaa, na hata nguvu yoyote itasababisha muda mzuri.

Zoezi$\PageIndex{2}$

Andika maneno matano ya kwanza ya mlolongo:

$a_n=\dfrac{4n}{{(−2)}^n}$

Jibu: Masharti tano ya kwanza ni$\{−2, 2, −32, 1, −58\}$.

Kuchunguza Piecewise wazi formula

Tumejifunza kwamba utaratibu ni kazi ambao uwanja wake ni juu ya integers chanya. Hii ni kweli kwa aina nyingine za kazi, ikiwa ni pamoja na baadhi ya kazi za kipande. Kumbuka kwamba kazi piecewise ni kazi inavyoelezwa na vifungu vingi. formula tofauti inaweza kuwakilisha kila kifungu cha mtu binafsi.

Jinsi ya: Kutokana na formula wazi kwa ajili ya kazi piecewise, kuandika kwanza$n$ terms of a sequence

Tambua formula ambayo$n=1$ inatumika.
Ili kupata muda wa kwanza$a_1$, tumia$n=1$ katika formula sahihi.
Tambua formula ambayo$n=2$ inatumika.
Ili kupata muda wa pili$a_2$, tumia$n=2$ katika fomu inayofaa.
Endelea kwa namna ile ile mpaka utakapotambua$n$ masharti yote.

Mfano$\PageIndex{3}$: Writing the Terms of a Sequence Defined by a Piecewise Explicit Formula

Andika maneno sita ya kwanza ya mlolongo.

$a_n=\begin{cases}n^2\space \text{if n is not divisible by } 3\\\dfrac{n}{3} \text{if n is divisible by } 3\end{cases}$

Suluhisho

Mbadala$n=1$,$n=2$, na kadhalika katika formula sahihi. Matumizi$n^2$ wakati$n$ si nyingi ya$3$. Matumizi$n^3$ wakati$n$ ni nyingi ya$3$.

$\begin{array}{ll} a_1=1^2=1 & 1 \text{ is not a multiple of }3. \text{ Use } n^2. \\ a_2=2^2=4 & 2 \text{ is not a multiple of }3 \text{ . Use }n^2. \\ a_3=\dfrac{3}{3}=1 & 3 \text{ is a multiple of }3 \text{. Use }\dfrac{n}{3}. \\ a_4=4^2=16 & 4 \text{ is not a multiple of }3. \text{ Use }n^2. \\ a_5=5^2=25 & 5 \text{ is not a multiple of } 3. \text{Use }n^2. \\ a_6=\dfrac{6}{3}=2 & 6 \text{ is a multiple of }3. \text{Use }\dfrac{n}{3} \end{array}$

Masharti sita ya kwanza ni$\{1, 4, 1, 16, 25, 2\}$.

Uchambuzi

Kila hatua ya tatu kwenye grafu iliyoonyeshwa kwenye Kielelezo$\PageIndex{4}$ inasimama kutoka kwenye pointi mbili zilizo karibu. Hii hutokea kwa sababu mlolongo ulifafanuliwa na kazi piecewise.

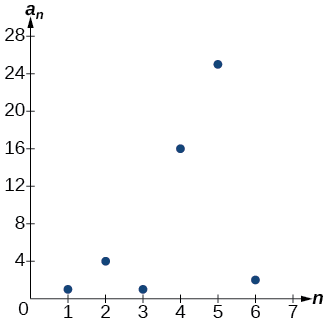
$Grafu ya njama iliyotawanyika ambapo x-axis ni lebo n na y-axis ni lebo a_n.$

Kielelezo$\PageIndex{4}$

Zoezi$\PageIndex{3}$

Andika maneno sita ya kwanza ya mlolongo.

$a_n=\begin{cases}2n^3 \text{ if } n\text{ is odd} \\ \dfrac{5n}{2} \text{ if } n \text{ is even}\end{cases}$

Jibu: Masharti sita ya kwanza ni$\{2, 5, 54, 10, 250, 15\}$.

Kutafuta Mfumo wa wazi

Hadi sasa, tumepewa formula wazi na kuulizwa kupata idadi ya masharti ya mlolongo. Wakati mwingine, formula wazi kwa muda wa nth wa mlolongo haipatikani. Badala yake, tunapewa maneno kadhaa kutoka kwa mlolongo. Wakati hii itatokea, tunaweza kufanya kazi katika reverse kupata formula wazi kutoka masharti ya kwanza chache ya mlolongo. Funguo la kutafuta formula wazi ni kuangalia mfano katika maneno. Kumbuka kwamba muundo unaweza kuhusisha alternating maneno, formula kwa ajili ya nambari, formula kwa denominators, exponents, au besi.

Jinsi ya: Kutokana na masharti machache ya mlolongo, pata formula wazi kwa mlolongo

Angalia mfano kati ya maneno.
Ikiwa maneno ni sehemu ndogo, angalia mfano tofauti kati ya nambari na denominators.
Angalia mfano kati ya ishara za maneno.
Andika formula$a_n$ kwa suala la$n$. Mtihani formula yako kwa$n=1$$n=2$,, na$n=3$.

Mfano$\PageIndex{4}$: Writing an Explicit Formula for the nth Term of a Sequence

Andika formula wazi kwa muda wa nth wa kila mlolongo.

$\{−\dfrac{2}{11}, \dfrac{3}{13}, −\dfrac{4}{15}, \dfrac{5}{17}, −\dfrac{6}{19},…\}$
$\{−\dfrac{2}{25}, −\dfrac{2}{125}, −\dfrac{2}{625}, −\dfrac{2}{3,125}, −\dfrac{2}{15,625},…\}$
$\{e^4,e^5,e^6,e^7,e^8,…\}$

Suluhisho

Angalia mfano katika kila mlolongo.

Masharti yanabadilisha kati ya chanya na hasi. Tunaweza kutumia${(−1)}^n$ ili kufanya maneno mbadala. Nambari inaweza kuwakilishwa na$n+1$. Denominator inaweza kuwakilishwa na$2n+9$.
$a_n=\dfrac{{(−1)}^n(n+1)}{2n+9}$
Masharti yote ni hasi.
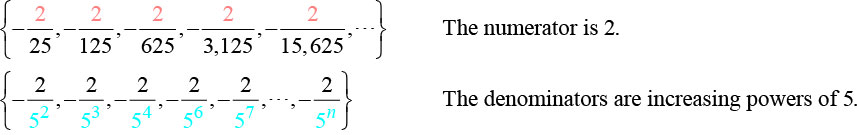
Kwa hiyo tunajua kwamba sehemu ni hasi, namba ni$2$, na denominator inaweza kuwakilishwa na$5n+1$.

$a_n=−\dfrac{2}{5^{n+1}}$
Masharti ni nguvu ya$e$. Kwa$n=1$, muda wa kwanza ni$e^4$ hivyo exponent lazima$n+3$.
$a_n=e^{n+3}$

Zoezi$\PageIndex{4A}$

Andika formula wazi kwa muda wa nth wa mlolongo.

$\{9,−81,729,−6,561,59,049,…\}$

Jibu: $a_n={(−1)}^{n+1}9^n$

Zoezi$\PageIndex{4B}$

Andika formula wazi kwa muda wa nth wa mlolongo.

$\{−34,−98,−2712,−8116,−24320,...\}$

Jibu: $a_n=−\dfrac{3^n}{4n}$

Zoezi$\PageIndex{4C}$

Andika formula wazi kwa muda wa nth wa mlolongo.

$\left \{ \dfrac{1}{e^2}, \dfrac{1}{e}, 1, e, e^2,... \right \}$

Jibu: $a_n=e^{n−3}$

Kuandika Masharti ya Mlolongo Inafafanuliwa na Mfumo wa Kurudia

Utaratibu hutokea kiasili katika mifumo ya ukuaji wa maganda ya nautilus, pinecones, matawi ya miti, na miundo mingine mingi ya asili. Tunaweza kuona mlolongo katika mpangilio wa jani au tawi, idadi ya petals ya maua, au mfano wa vyumba katika shell ya nautilus. Ukuaji wao unafuata mlolongo wa Fibonacci, mlolongo maarufu ambao kila neno linaweza kupatikana kwa kuongeza masharti mawili yaliyotangulia. idadi katika mlolongo ni mifano$1, 1, 2, 3, 5, 8, 13, 21, 34,….$ mingine kutoka dunia ya asili kwamba kuonyesha mlolongo Fibonacci ni Calla Lily, ambayo ina petal moja tu, Black Eyed Susan na$13$ petals, na aina tofauti ya daisies ambayo inaweza kuwa$21$ au$34$ petals.

Kila muda wa mlolongo wa Fibonacci unategemea maneno ambayo huja kabla yake. Mlolongo wa Fibonacci hauwezi kuandikwa kwa urahisi kwa kutumia formula wazi. Badala yake, tunaelezea mlolongo kwa kutumia formula ya kujirudia, formula inayofafanua masharti ya mlolongo kwa kutumia maneno ya awali.

Fomu ya kujirudia daima ina sehemu mbili: thamani ya muda wa awali (au maneno), na equation inayofafanua$a_n$ kwa suala la maneno yaliyotangulia. Kwa mfano, tuseme tunajua yafuatayo:

\[\begin{align*} a_1 &= 3 \\ a_n &= 2a_{n−1}−1 , \text{ for }n≥2 \end{align*}\]

Tunaweza kupata masharti yafuatayo ya mlolongo kwa kutumia muda wa kwanza.

\[\begin{align*} a_1 &= 3 \\ a_2 &= 2a_1−1=2(3)−1=5 \\ a_3 &= 2a_2−1=2(5)−1=9 \\ a_4 &= 2a_3−1=2(9)−1=17 \end{align*}\]

Hivyo masharti manne ya kwanza ya mlolongo ni$\{3, 5, 9, 17\}$.

Fomu ya kujirudia kwa mlolongo wa Fibonacci inasema maneno mawili ya kwanza na hufafanua kila neno mfululizo kama jumla ya maneno mawili yaliyotangulia.

\[\begin{align*}a_1 &= 1 \\ a_2 &= 1 \\ a_n &= a_{n−1}+a_{n−2} \text{, for }n≥3 \end{align*}\]

Ili kupata muda wa kumi wa mlolongo, kwa mfano, tunahitaji kuongeza maneno ya nane na ya tisa. Tuliambiwa hapo awali kwamba suala la nane na tisa ni$34$,$21$ na hivyo

$a_{10}=a_9+a_8=34+21=55$

FORMULA YA KURUDIA

Fomula ya kujirudia ni formula inayofafanua kila neno la mlolongo kwa kutumia muda (s) uliopita. Fomu za kujirudia lazima zieleze muda wa awali, au maneno, ya mlolongo.

Q & A: Lazima maneno mawili ya kwanza yatolewe kwa formula ya kujirudia?

Hapana. Mlolongo wa Fibonacci unafafanua kila neno kwa kutumia maneno mawili yaliyotangulia, lakini formula nyingi za kujirudia hufafanua kila neno kwa kutumia muda mmoja tu uliopita. Utaratibu huu unahitaji tu muda wa kwanza kufafanuliwa.

Jinsi ya: Kutokana na formula kujirudia na tu muda wa kwanza zinazotolewa, kuandika kwanza n suala la mlolongo

Tambua muda wa awali$a_1$, ambao hutolewa kama sehemu ya formula. Huu ndio neno la kwanza.
Ili kupata muda wa pili$a_2$, badala ya muda wa awali katika formula kwa$a_{n−1}$. Kutatua.
Ili kupata muda wa tatu$a_3$, badala ya muda wa pili katika formula. Kutatua.
Kurudia mpaka utatuliwa kwa muda wa nth.

Mfano$\PageIndex{5}$: Writing the Terms of a Sequence Defined by a Recursive Formula

Andika maneno matano ya kwanza ya mlolongo unaofafanuliwa na formula ya kujirudia.

\[\begin{align*}a_1 &= 9 \\ a_n &= 3a_{n−1}−20 , \text{ for }n≥2 \end{align*}\]

Suluhisho

Neno la kwanza linatolewa katika formula. Kwa kila muda unaofuata, tunachukua nafasi$a_n−1$ na thamani ya muda uliopita.

$\begin{array}{ll} n=1 & a_1=9 \\ n=2 & a_2=3a_1−20=3(9)−20=27−20=7 \\ n=3 & a_3=3a_2−20=3(7)−20=21−20=1 \\ n=4 & a_4=3a_3−20=3(1)−20=3−20=−17 \\ n=5 & a_5=3a_4−20=3(−17)−20=−51−20=−71 \end{array}$

Masharti tano ya kwanza ni$\{9, 7, 1, –17, –71\}$. Angalia Kielelezo$\PageIndex{5}$.

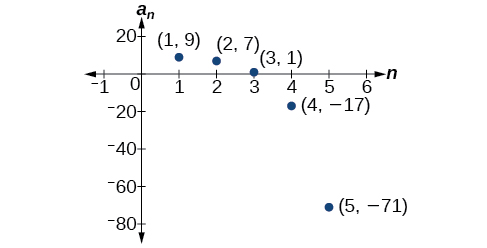
$Grafu ya njama iliyotawanyika na pointi zilizoandikwa: (1, 9), (2, 7), (3, 1), (4, -17), na (5, -71). Mhimili wa x umeandikwa n na mhimili wa y umeandikwa a_n.$

Kielelezo$\PageIndex{5}$

Zoezi$\PageIndex{5}$

Andika maneno matano ya kwanza ya mlolongo unaofafanuliwa na formula ya kujirudia.

\[\begin{align*} a_1 &= 2 \\ a_n &= 2a_{n−1}+1 , \text{ for }n≥2 \end{align*}\]

Jibu: $\{2, 5, 11, 23, 47\}$

Jinsi ya: Kutokana na formula ya kujirudia na maneno mawili ya awali, andika kwanza$n$ terms of a sequence

Tambua muda wa awali$a_1$, ambao hutolewa kama sehemu ya formula.
Tambua muda wa pili$a_2$, ambao hutolewa kama sehemu ya formula.
Ili kupata muda wa tatu, badala ya muda wa awali na muda wa pili katika formula. Tathmini.
Rudia mpaka uwe na tathmini ya muda wa nth.

Mfano$\PageIndex{6}$: Writing the Terms of a Sequence Defined by a Recursive Formula

Andika maneno sita ya kwanza ya mlolongo unaofafanuliwa na formula ya kujirudia.

\[\begin{align*} a_1 &=1 \\ a_2 &= 2 \\ a_n &= 3a_{n−1}+4a_{n−2} , \text{ for }n≥3 \end{align*}\]

Suluhisho

Masharti mawili ya kwanza yanatolewa. Kwa kila muda unaofuata, tunachukua nafasi$a_{n−1}$$a_{n−2}$ na kwa maadili ya maneno mawili yaliyotangulia.

$\begin{array}{ll} n=3 & a_3=3a_2+4a_1=3(2)+4(1)=10 \\ n=4 & a_4=3a_3+4a_2=3(10)+4(2)=38 \\ n=5 & a_5=3a_4+4a_3=3(38)+4(10)=154 \\ n=6 & a_6=3a_5+4a_4=3(154)+4(38)=614 \end{array}$

Masharti sita ya kwanza ni$\{1,2,10,38,154,614\}$. Angalia Kielelezo$\PageIndex{6}$.

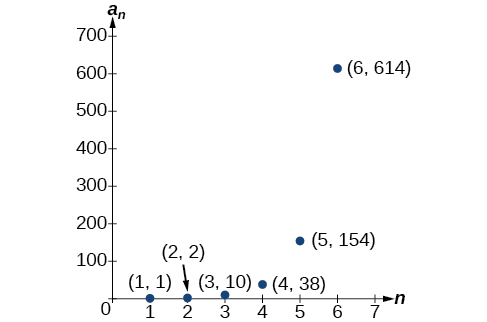
$Grafu ya njama iliyotawanyika na pointi zilizoandikwa: (1, 1), (2, 2), (3, 10), (4, 38), (5, 154) na (6, 614). Mhimili wa x umeandikwa n na mhimili wa y umeandikwa a_n.$

Kielelezo$\PageIndex{6}$

Zoezi$\PageIndex{6}$

Andika$8$ maneno ya kwanza ya mlolongo unaofafanuliwa na formula ya kujirudia.

\[\begin{align*}a_1 &= 0 \\ a_2 &= 1 \\ a_3 &= 1 \\ a_n &= \dfrac{a_{n−1}}{a_{n−2}}+a_{n−3} , \text{ for }n≥4 \end{align*}\]

Jibu: $\left \{0, 1, 1, 1, 2, 3, 52, 176 \right \}$.

Kutumia Nukuu ya Kielelezo

Fomu za utaratibu fulani ni pamoja na bidhaa za integers mfululizo mzuri. $n$factorial, imeandikwa kama$n!$, ni bidhaa ya integers chanya kutoka$1$ kwa$n$. Kwa mfano,

\[\begin{align*}4! &= 4⋅3⋅2⋅1=24 \\ 5! &= 5⋅4⋅3⋅2⋅1=120 \end{align*}\]

Mfano wa formula iliyo na factorial ni$a_n=(n+1)!$. Muda wa sita wa mlolongo unaweza kupatikana$6$ kwa kubadili$n$.

$a_6=(6+1)!=7!=7·6·5·4·3·2·1=5040$

factorial ya idadi yoyote yote$n$ ni$n(n−1)!$ Tunaweza kwa hiyo pia kufikiria$5!$ kama$5⋅4!$.

FACTORIAL

$n$factorial ni operesheni ya hisabati ambayo inaweza kuelezwa kwa kutumia formula kujirudia. factorial ya$n$, ulionyehsa$n!$, hufafanuliwa kwa integer chanya$n$ kama:

\[\begin{align} 0! &= 1 \\ 1! &= 1 \\ n! &= n(n−1)(n−2)⋯(2)(1), \text{ for }n≥2 \end{align}\]

Kesi maalum$0!$ hufafanuliwa kama$0!=1$.

Q & A: Je, factorials daima kupatikana kwa kutumia calculator?

Hapana. Factorials kupata kubwa haraka sana-kasi kuliko hata kazi kielelezo! Wakati pato inapata kubwa mno kwa calculator, haitaweza kuhesabu factorial.

Mfano$\PageIndex{7}$: Writing the Terms of a Sequence Using Factorials

Andika maneno matano ya kwanza ya mlolongo unaofafanuliwa na formula iliyo wazi$a_n=\dfrac{5n}{(n+2)!}$.

Suluhisho

Mbadala$n=1$,$n=2$, na kadhalika katika formula.

$\begin{array}{ll} n=1 & a_1=\dfrac{5(1)}{(1+2)!}=\dfrac{5}{3!}=\dfrac{5}{3·2·1}=\dfrac{5}{6} \\ n=2 & a_2=\dfrac{5(2)}{(2+2)!}=\dfrac{10}{4!}=\dfrac{10}{4·3·2·1}=\dfrac{5}{12} \\ n=3 & a_3=\dfrac{5(3)}{(3+2)!}=\dfrac{15}{5!}=\dfrac{15}{5·4·3·2·1}=\dfrac{1}{8} \\ n=4 & a_4=\dfrac{5(4)}{(4+2)!}=\dfrac{20}{6!}=\dfrac{20}{6·5·4·3·2·1}=\dfrac{1}{36} \\ n=5 & a_5=\dfrac{5(5)}{(5+2)!}=\dfrac{25}{7!}=\dfrac{25}{7·6·5·4·3·2·1}=\dfrac{5}{1,008} \end{array}$

Masharti tano ya kwanza ni$\left \{\dfrac{5}{6}, \dfrac{5}{12}, \dfrac{1}{8}, \dfrac{1}{36}, \dfrac{5}{1,008} \right \}$.

Uchambuzi

Kielelezo$\PageIndex{7}$ kinaonyesha grafu ya mlolongo. Kumbuka kwamba, kwa kuwa factorials kukua kwa haraka sana, uwepo wa neno factorial katika denominator matokeo katika denominator kuwa kubwa zaidi kuliko nambari kama nn inavyoongezeka. Hii inamaanisha kuwa quotient inapungua na, kama njama ya maneno inaonyesha, maneno yanapungua na inakaribia sifuri.

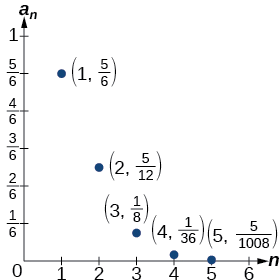
$13.2.7.pngGrafu ya njama iliyotawanyika yenye alama zilizoandikwa: (1, 5/6), (2, 5/12), (3, 1/8), (4, 1/36), na (5, 5/1008). Mhimili wa x umeandikwa n na mhimili wa y umeandikwa a_n.$

Kielelezo$\PageIndex{7}$

Zoezi$\PageIndex{7}$

Andika maneno matano ya kwanza ya mlolongo unaofafanuliwa na formula iliyo wazi$a_n=\dfrac{(n+1)!}{2n}$.

Jibu: Masharti tano ya kwanza ni$\left \{1, \dfrac{3}{2}, 4, 15, 72 \right \}$.

Media

Kupata rasilimali hii online kwa maelekezo ya ziada na mazoezi na Utaratibu.

Kupata Masharti katika Mlolongo

Mlinganyo muhimu

Mfumo wa factorial

$0!=1$

$1!=1$

$n!=n(n−1)(n−2)⋯(2)(1)$, kwa$n≥2$

Dhana muhimu

Mlolongo ni orodha ya namba, inayoitwa maneno, iliyoandikwa kwa utaratibu maalum.
Fomula wazi hufafanua kila neno la mlolongo kwa kutumia nafasi ya neno. Angalia Mfano$\PageIndex{1}$, Mfano$\PageIndex{2}$, na Mfano$\PageIndex{3}$.
Fomu ya wazi kwa muda wa nth wa mlolongo inaweza kuandikwa kwa kuchambua muundo wa maneno kadhaa. Angalia Mfano$\PageIndex{4}$.
Fomula za kujirudia hufafanua kila neno la mlolongo kwa kutumia maneno ya awali.
Fomu za kujirudia lazima zieleze muda wa awali, au maneno, ya mlolongo.
Seti ya maneno yanaweza kuandikwa kwa kutumia formula ya kujirudia. Angalia Mfano$\PageIndex{5}$ na Mfano$\PageIndex{6}$.
factorial ni operesheni ya hisabati ambayo inaweza kuelezwa recursively.
factorial ya$n$ ni bidhaa ya integers wote kutoka$1$ kwa$n$. Angalia Mfano$\PageIndex{7}$.

Contributors and Attributions

Template:ContribOpenStaxPreCalc

\(n\)	1	2	3	4	5	\(n\)
\(n^{th}\)muda wa mlolongo,\(a_n\)	2	4	8	16	32	\(2^n\)

MLOLONGO

Q & A: Je, mlolongo daima unapaswa kuanza na\(a_1\)?

Jinsi ya: Kutokana na formula wazi, kuandika kwanza\(n\) terms of a sequence

Mfano\(\PageIndex{1}\): Writing the Terms of a Sequence Defined by an Explicit Formula

Zoezi\(\PageIndex{1}\)

Jinsi ya: Kutokana na formula wazi na maneno mbadala, kuandika masharti ya kwanza ya nn ya mlolongo

Mfano\(\PageIndex{2}\): Writing the Terms of an Alternating Sequence Defined by an Explicit Formula

Zoezi\(\PageIndex{2}\)

Jinsi ya: Kutokana na formula wazi kwa ajili ya kazi piecewise, kuandika kwanza\(n\) terms of a sequence

Mfano\(\PageIndex{3}\): Writing the Terms of a Sequence Defined by a Piecewise Explicit Formula

Zoezi\(\PageIndex{3}\)

Jinsi ya: Kutokana na masharti machache ya mlolongo, pata formula wazi kwa mlolongo

Mfano\(\PageIndex{4}\): Writing an Explicit Formula for the nth Term of a Sequence

Zoezi\(\PageIndex{4A}\)

Zoezi\(\PageIndex{4B}\)

Zoezi\(\PageIndex{4C}\)

FORMULA YA KURUDIA

Q & A: Lazima maneno mawili ya kwanza yatolewe kwa formula ya kujirudia?

Mfano\(\PageIndex{5}\): Writing the Terms of a Sequence Defined by a Recursive Formula

Zoezi\(\PageIndex{5}\)

Mfano\(\PageIndex{6}\): Writing the Terms of a Sequence Defined by a Recursive Formula

Zoezi\(\PageIndex{6}\)

FACTORIAL

Q & A: Je, factorials daima kupatikana kwa kutumia calculator?

Mfano\(\PageIndex{7}\): Writing the Terms of a Sequence Using Factorials

Zoezi\(\PageIndex{7}\)

Jedwali\(\PageIndex{3}\)
\(n\)	1	2	3	4	5
\(a_n\)	5	2	-1	—4	—7

Malengo ya kujifunza

Kuandika Masharti ya Mlolongo Imeelezwa na Mfumo wa wazi

MLOLONGO

Jinsi ya: Kutokana na formula wazi, kuandika kwanza\(n\) terms of a sequence

Mfano\(\PageIndex{1}\): Writing the Terms of a Sequence Defined by an Explicit Formula

Zoezi\(\PageIndex{1}\)

Kuchunguza Utaratibu mbadala

Jinsi ya: Kutokana na formula wazi na maneno mbadala, kuandika masharti ya kwanza ya nn ya mlolongo

Mfano\(\PageIndex{2}\): Writing the Terms of an Alternating Sequence Defined by an Explicit Formula

Q & A: Katika mfano hapo juu, je\((–1)\) to the power of \(n\) account for the oscillations of signs?

Zoezi\(\PageIndex{2}\)

Kuchunguza Piecewise wazi formula

Jinsi ya: Kutokana na formula wazi kwa ajili ya kazi piecewise, kuandika kwanza\(n\) terms of a sequence

Mfano\(\PageIndex{3}\): Writing the Terms of a Sequence Defined by a Piecewise Explicit Formula

Zoezi\(\PageIndex{3}\)

Kutafuta Mfumo wa wazi

Jinsi ya: Kutokana na masharti machache ya mlolongo, pata formula wazi kwa mlolongo

Mfano\(\PageIndex{4}\): Writing an Explicit Formula for the nth Term of a Sequence

Zoezi\(\PageIndex{4A}\)

Zoezi\(\PageIndex{4B}\)

Zoezi\(\PageIndex{4C}\)

Kuandika Masharti ya Mlolongo Inafafanuliwa na Mfumo wa Kurudia

Jinsi ya: Kutokana na formula kujirudia na tu muda wa kwanza zinazotolewa, kuandika kwanza n suala la mlolongo

Mfano\(\PageIndex{5}\): Writing the Terms of a Sequence Defined by a Recursive Formula

Zoezi\(\PageIndex{5}\)

Jinsi ya: Kutokana na formula ya kujirudia na maneno mawili ya awali, andika kwanza\(n\) terms of a sequence

Mfano\(\PageIndex{6}\): Writing the Terms of a Sequence Defined by a Recursive Formula

Zoezi\(\PageIndex{6}\)

Kutumia Nukuu ya Kielelezo

FACTORIAL

Mfano\(\PageIndex{7}\): Writing the Terms of a Sequence Using Factorials

Zoezi\(\PageIndex{7}\)

Media

Mlinganyo muhimu

Dhana muhimu

Contributors and Attributions