10.8E: Vectors (Mazoezi)

Last updated
Save as PDF

Page ID: 178529

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Kwa mazoezi yafuatayo, onyesha kama vectors mbili,$\mathbf{u}$ na$\mathbf{v},$ ni sawa, ambapo$\mathbf{u}$ ina hatua ya awali$P_{1}$ na hatua ya mwisho$P_{2},$ na$\mathbf{v}$ ina hatua ya awali$P_{3}$ na hatua ya mwisho$P_{4}$.

52. $P_{1}=(-1,4), P_{2}=(3,1), P_{3}=(5,5)$na$P_{4}=(9,2)$

53. $P_{1}=(6,11), P_{2}=(-2,8), P_{3}=(0,-1)$na$P_{4}=(-8,2)$

Kwa mazoezi yafuatayo, tumia vectors$\mathbf{u}=2 \mathbf{i}-\mathbf{j}, \mathbf{v}=4 \mathbf{i}-3 \mathbf{j},$ na$w=-2 \mathbf{i}+5 \mathbf{j}$ kutathmini maneno.

54. $u-v$

55. $2 v-u+w$

Kwa mazoezi yafuatayo, pata vector kitengo katika mwelekeo sawa na vector iliyotolewa.

56. $a=8 i-6 j$

57. $b=-3 i-j$

Kwa mazoezi yafuatayo, pata ukubwa na mwelekeo wa vector.

58. $\langle 6,-2\rangle$

59. $\langle-3,-3\rangle$

Kwa mazoezi yafuatayo, hesabu$\mathbf{u} \cdot \mathbf{v}$.

60. $u=-2 i+j$na$v=3 i+7 j$

61. $u=i+4 j$na$v=4 i+3 j$

62. Kutokana na$\boldsymbol{v}=\langle-3,4\rangle$ kuteka$\boldsymbol{v}, 2 \boldsymbol{v},$ na$\frac{1}{2} \boldsymbol{v}$

63. Kutokana na wadudu inavyoonekana katika Kielelezo 4, mchoro$\boldsymbol{u}+\boldsymbol{v}, \boldsymbol{u}-\boldsymbol{v}$ na$3 \boldsymbol{v}$.

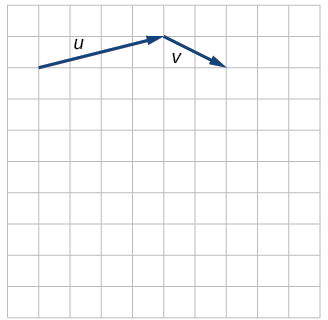
$Mchoro wa vectors v, 2v, na 1/2 v. vector 2v iko katika mwelekeo sawa na v lakini ina ukubwa mara mbili. the 1/2 v vector ni katika mwelekeo sawa na v lakini ina nusu ukubwa.$

Kielelezo 4

64. Kutokana$P_{1}=(3,2)$ na hatua ya awali na hatua ya mwisho$P_{2}=(-5,-1),$ kuandika vector$\mathbf{v}$ katika suala la$\mathbf{i}$ na$\mathbf{j}$. Chora pointi na vector kwenye grafu.