10.8: Vectors
- Page ID
- 178508
- Tazama wadudu kijiometri.
- Pata ukubwa na mwelekeo.
- Kufanya kuongeza vector na kuzidisha scalar.
- Pata fomu ya sehemu ya vector.
- Kupata kitengo vector katika mwelekeo wa\(v\).
- Kufanya shughuli na wadudu katika suala la\(i\) na\(j\).
- Pata bidhaa ya dot ya vectors mbili.
ndege ni flying katika airspeed ya\(200\) maili kwa saa inaongozwa juu ya kuzaa SE ya\(140°\). Upepo wa kaskazini (kutoka kaskazini hadi kusini) unapiga\(16.2\) maili kwa saa, kama inavyoonekana kwenye Kielelezo\(\PageIndex{1}\). Je! Kasi ya ardhi na kuzaa halisi ya ndege ni nini?
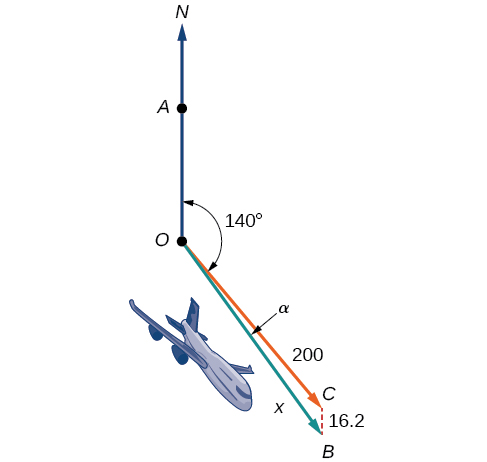
Kielelezo\(\PageIndex{1}\)
Kasi ya chini inahusu kasi ya ndege ikilinganishwa na ardhi. Airspeed inahusu kasi ndege inayoweza kusafiri ikilinganishwa na molekuli yake ya hewa inayozunguka. Kiasi hiki mbili si sawa kwa sababu ya athari za upepo. Katika sehemu ya awali, tulitumia pembetatu kutatua tatizo sawa linalohusisha harakati za boti. Baadaye katika sehemu hii, tutapata kasi ya ardhi ya ndege na kuzaa, wakati wa kuchunguza njia nyingine ya matatizo ya aina hii. Kwanza, hata hivyo, hebu tuchunguze misingi ya vectors.
Mtazamo wa Kijiometri wa Vectors
Vector ni kiasi maalum inayotolewa kama sehemu ya mstari na mshale kwenye mwisho mmoja. Ina hatua ya awali, ambapo huanza, na hatua ya mwisho, ambapo inaisha. Vector inaelezwa na ukubwa wake, au urefu wa mstari, na mwelekeo wake, unaonyeshwa na kichwa cha mshale kwenye hatua ya mwisho. Hivyo, vector ni sehemu iliyoelekezwa ya mstari. Kuna alama mbalimbali zinazotofautisha wadudu kutoka kwa kiasi kingine:
- Kesi ya chini, aina ya ujasiri, na au bila mshale juu kama vile \(u\)\(w\),\(\overrightarrow{v}\),\(\overrightarrow{u}\),\(\overrightarrow{w}\).
- Kutokana hatua ya awali\(P\) na uhakika terminal\(Q\), vector inaweza kuwakilishwa kama\(\overrightarrow{PQ}\). Mshale juu ni nini kinaonyesha kwamba si tu mstari, lakini sehemu ya mstari iliyoongozwa.
- Kutokana hatua ya awali ya\((0,0)\) na terminal uhakika\((a,b)\), vector inaweza kuwakilishwa kama\(⟨a,b⟩\).
Ishara hii ya mwisho\(⟨a,b⟩\) ina umuhimu maalum. Inaitwa nafasi ya kawaida. Vector ya msimamo ina hatua ya awali\((0,0)\) na hatua ya mwisho\(⟨a,b⟩\). Ili kubadilisha vector yoyote katika vector nafasi, tunafikiri juu ya mabadiliko katika x -kuratibu na mabadiliko katika y -kuratibu. Hivyo, kama hatua ya awali ya vector\(\overrightarrow{CD}\) ni\(C(x_1,y_1)\) na hatua ya mwisho ni\(D(x_2,y_2)\), basi vector nafasi inapatikana kwa kuhesabu
\[\begin{align*} \overrightarrow{AB} &= ⟨x_2−x_1,y_2−y_1⟩ \\[4pt] &= ⟨a,b⟩ \end{align*}\]
Katika Kielelezo\(\PageIndex{2}\), tunaona vector ya awali\(\overrightarrow{CD}\) na vector nafasi\(\overrightarrow{AB}\).
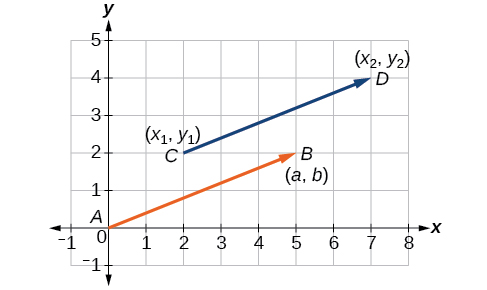
Kielelezo\(\PageIndex{2}\)
Vector ni sehemu iliyoelekezwa ya mstari na hatua ya awali na hatua ya mwisho. Vectors hutambuliwa kwa ukubwa, au urefu wa mstari, na mwelekeo, unaowakilishwa na kichwa cha mshale kinachoelekea kuelekea hatua ya mwisho. Vector ya msimamo ina hatua ya awali\((0,0)\) na inatambuliwa na hatua yake ya mwisho\(⟨a,b⟩\).
Fikiria vector ambao hatua ya awali ni\(P(2,3)\) na uhakika wa mwisho ni\(Q(6,4)\). Kupata msimamo vector.
Suluhisho
Vector msimamo hupatikana kwa kuondoa moja\(x\) -kuratibu kutoka nyingine\(x\) -kuratibu, na moja\(y\) -kuratibu kutoka nyingine\(y\) -kuratibu. Hivyo
\[\begin{align*} v &= ⟨6−2,4−3⟩ \\[4pt] &=⟨4,1⟩ \end{align*}\]
vector msimamo huanza saa\((0,0)\) na kumalizika saa\((4,1)\). Grafu ya vectors zote mbili zinaonyeshwa kwenye Kielelezo\(\PageIndex{3}\).
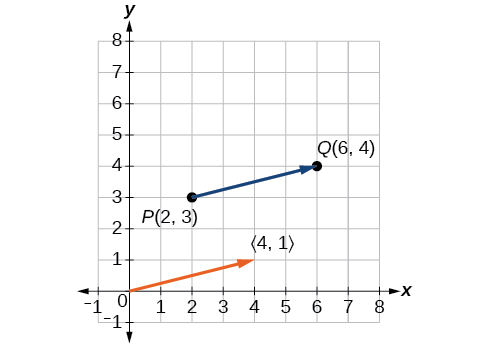
Kielelezo\(\PageIndex{3}\)
Tunaona kwamba vector msimamo ni\(⟨4,1⟩\).
Kupata msimamo vector kutokana na kwamba vector\(v\) ina hatua ya awali katika\((−3,2)\) na uhakika terminal katika\((4,5)\), kisha grafu wadudu wote katika ndege moja.
Suluhisho
Vector msimamo hupatikana kwa kutumia hesabu zifuatazo:
\[\begin{align*} v &= ⟨4−(−3),5−2⟩ \\[4pt] &= ⟨7,3⟩ \end{align*}\]
Hivyo, vector nafasi huanza saa\((0,0)\) na kumalizika saa\((7,3)\). Angalia Kielelezo\(\PageIndex{4}\).
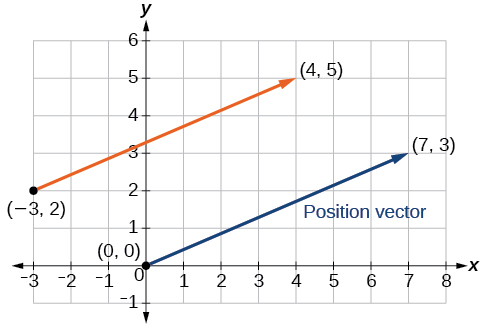
Kielelezo\(\PageIndex{4}\)
Chora vector\(\vec{v}\) inayounganisha kutoka asili hadi hatua\((3,5)\).
- Jibu
-
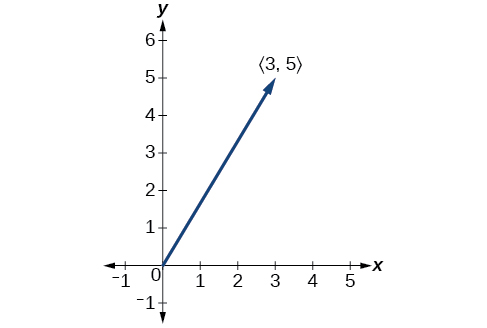
Kielelezo\(\PageIndex{5}\)
Kupata Ukubwa na Mwelekeo
Kufanya kazi na vector, tunahitaji kuwa na uwezo wa kupata ukubwa wake na mwelekeo wake. Tunapata ukubwa wake kwa kutumia Theorem ya Pythagorean au formula ya umbali, na tunapata mwelekeo wake kwa kutumia kazi ya tangent inverse.
Kutokana na vector nafasi\(\vec{v}=⟨a,b⟩\), ukubwa hupatikana\(| v |=\sqrt{a^2+b^2}\) na.Mwelekeo ni sawa na angle iliyoundwa na\(x\) -axis, au kwa\(y\) -axis, kulingana na programu. Kwa vector msimamo, mwelekeo hupatikana na\(\tan \theta=\left(\dfrac{b}{a}\right)⇒\theta={\tan}^{−1}\left(\dfrac{b}{a}\right)\), kama inavyoonekana katika Kielelezo\(\PageIndex{6}\).
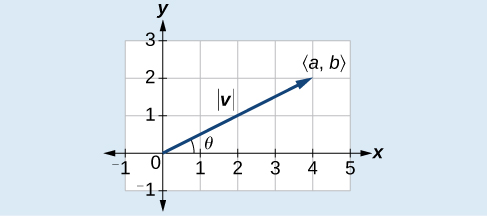
Kielelezo\(\PageIndex{6}\)
Vectors mbili\(\vec{v}\) na\(\vec{u}\) huchukuliwa kuwa sawa ikiwa wana ukubwa sawa na mwelekeo huo. Zaidi ya hayo, ikiwa wadudu wote wana vector sawa msimamo, wao ni sawa.
Pata ukubwa na mwelekeo wa vector na hatua ya awali\(P(−8,1)\) na hatua ya terminal\(Q(−2,−5)\) .Chora vector.
Suluhisho
Kwanza, pata vector ya msimamo.
\[\begin{align*} u &= ⟨−2,−(−8),−5−1⟩ \\[4pt] &= ⟨6,−6⟩ \end{align*}\]
Tunatumia Theorem ya Pythagorean kupata ukubwa.
\[\begin{align*} |u| &= \sqrt{{(6)}^2+{(−6)}^2} \\[4pt] &= \sqrt{72} \\[4pt] &=\sqrt{62} \end{align*}\]
Mwelekeo hutolewa kama
\[\begin{align*} \tan \theta & =\dfrac{−6}{6}=−1\rightarrow \theta={\tan}^{−1}(−1) \\[4pt] &= −45° \end{align*}\]
Hata hivyo, angle imekoma katika quadrant ya nne, kwa hiyo tunaongeza\(360°\) kupata angle nzuri. Hivyo,\(−45°+360°=315°\). Angalia Kielelezo\(\PageIndex{7}\).
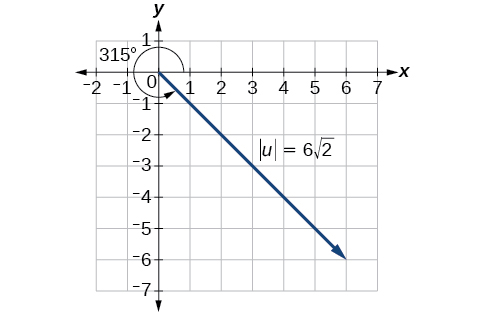
Kielelezo\(\PageIndex{7}\)
Onyesha kwamba vector\(\vec{v}\) na hatua ya awali katika\((5,−3)\) na terminal uhakika katika\((−1,2)\) ni sawa\(\vec{u}\) na vector na hatua ya awali katika\((−1,−3)\) na terminal uhakika katika\((−7,2)\). Chora vector msimamo kwenye gridi sawa\(\vec{v}\) na\(\vec{u}\). Kisha, pata ukubwa na mwelekeo wa kila vector.
Suluhisho
Kama inavyoonekana katika Kielelezo\(\PageIndex{8}\), kuteka vector\(\vec{v}\) kuanzia katika hatua ya awali\((5,−3)\) na terminal\((−1,2)\). Chora vector\(\vec{u}\) na hatua ya awali\((−1,−3)\) na hatua ya mwisho\((−7,2)\). Kupata nafasi ya kiwango kwa kila.
Next, kupata na mchoro nafasi vector kwa\(\vec{v}\) na\(\vec{u}\). Tuna
\[\begin{align*} v &= ⟨−1−5,2−(−3)⟩ \\[4pt] &= ⟨−6,5⟩u \\[4pt] &= ⟨−7−(−1),2−(−3)⟩ \\[4pt] & =⟨−6,5⟩ \end{align*}\]
Kwa kuwa vectors nafasi ni sawa,\(\vec{v}\) na\(\vec{u}\) ni sawa.
Njia mbadala ya kuangalia usawa wa vector ni kuonyesha kwamba ukubwa na mwelekeo ni sawa kwa wadudu wote. Ili kuonyesha kwamba ukubwa ni sawa, tumia Theorem ya Pythagorean.
\[\begin{align*} |v| &= \sqrt{{(−1−5)}^2+{(2−(−3))}^2} \\[4pt] &= \sqrt{{(−6)}^2+{(5)}^2} \\[4pt] &= \sqrt{36+25} \\[4pt] &= \sqrt{61} \\[4pt] |u| &= \sqrt{{(−7−(−1))}^2+{(2−(−3))}^2} \\[4pt] &=\sqrt{{(−6)}^2+{(5)}^2} \\[4pt] &= \sqrt{36+25} \\[4pt] &= \sqrt{61} \end{align*}\]
Kama ukubwa ni sawa, sasa tunahitaji kuthibitisha mwelekeo. Kutumia kazi ya tangent na vector nafasi inatoa
\[\begin{align*} \tan \theta &= −\dfrac{5}{6}⇒\theta={\tan}^{−1}\left(−\dfrac{5}{6}\right) \\[4pt] & = −39.8° \end{align*}\]
Hata hivyo, tunaweza kuona kwamba vector msimamo huisha katika roboduara ya pili, hivyo tunaongeza\(180°\). Hivyo, mwelekeo ni\(−39.8°+180°=140.2°\).
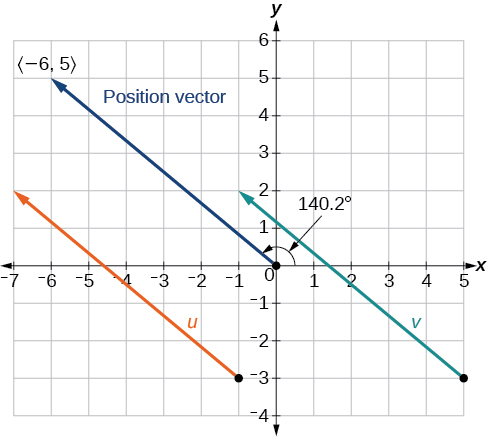
Kielelezo\(\PageIndex{8}\)
Kufanya Vector Aidha na Scalar Kuzidisha
Sasa kwa kuwa tunaelewa mali ya vectors, tunaweza kufanya shughuli zinazowashirikisha. Wakati ni rahisi kufikiria vector\(u=⟨x,y⟩\) kama mshale au sehemu iliyoongozwa mstari kutoka asili hadi hatua\((x,y)\), wadudu wanaweza kuwa iko mahali popote katika ndege. Jumla ya vectors mbili\(\vec{u}\) na\(\vec{v}\), au kuongeza vector, hutoa vector ya tatu\(\overrightarrow{u+ v}\), vector matokeo.
Ili kupata\(\overrightarrow{u + v}\), sisi kwanza kuteka vector\(\vec{u}\), na kutoka mwisho terminal ya\(\vec{u}\), sisi inayotolewa vector\(\vec{v}\). Kwa maneno mengine, tuna hatua ya awali ya\(\vec{v}\) kukutana mwisho terminal ya\(\vec{u}\). Msimamo huu unafanana na dhana kwamba tunahamia pamoja na vector ya kwanza na kisha, kutoka kwa hatua yake ya mwisho, tunahamia pamoja na vector ya pili. Jumla\(\overrightarrow{u + v}\) ni vector matokeo kwa sababu matokeo kutokana na kuongeza au kuondoa ya wadudu wawili. vector matokeo husafiri moja kwa moja kutoka mwanzo wa\(\vec{u}\) hadi mwisho wa\(\vec{v}\) katika njia moja kwa moja, kama inavyoonekana katika Kielelezo\(\PageIndex{9}\).
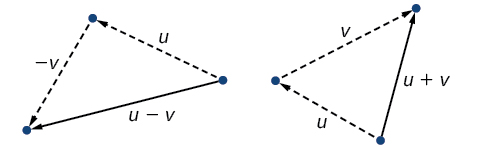
Kielelezo\(\PageIndex{9}\)
Kuondoa vector ni sawa na kuongeza vector. Ili kupata\(\overrightarrow{u − v}\), angalia kama\(\overrightarrow{u + (−v)}\). Kuongeza\(\overrightarrow{−v}\) ni kugeuza mwelekeo wa\(\vec{v}\) na kuongeza hadi mwisho wa\(\vec{u}\). vector mpya huanza mwanzoni mwa\(\vec{u}\) na ataacha katika hatua ya mwisho ya\(\overrightarrow{−v}\). Angalia Kielelezo\(\PageIndex{10}\) kwa Visual kwamba kulinganisha vector kuongeza na vector kutoa kutumia parallelograms.
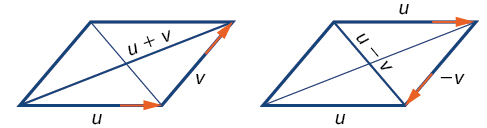
Kielelezo\(\PageIndex{10}\)
kutokana\(u=⟨3,−2⟩\) na\(v=⟨−1,4⟩\), kupata wadudu wawili mpya\(\overrightarrow{u + v}\), na\(\overrightarrow{u − v}\).
Suluhisho
Ili kupata jumla ya vectors mbili, tunaongeza vipengele. Hivyo,
\[ \begin{align*} u+v &= ⟨3,−2⟩+⟨−1,4⟩ \\[4pt] &= ⟨3+(−1),−2+4⟩ \\[4pt] &=⟨2,2⟩ \end{align*}\]
Angalia Kielelezo\(\PageIndex{11a}\).
Ili kupata tofauti ya vectors mbili, ongeza vipengele vibaya\(\vec{v}\) vya\(\vec{u}\). Hivyo,
\[\begin{align*}u+(−v) &=⟨3,−2⟩+⟨1,−4⟩ \\[4pt] &= ⟨3+1,−2+(−4)⟩ \\[4pt] &= ⟨4,−6⟩ \end{align*}\]
Angalia Kielelezo\(\PageIndex{11b}\).
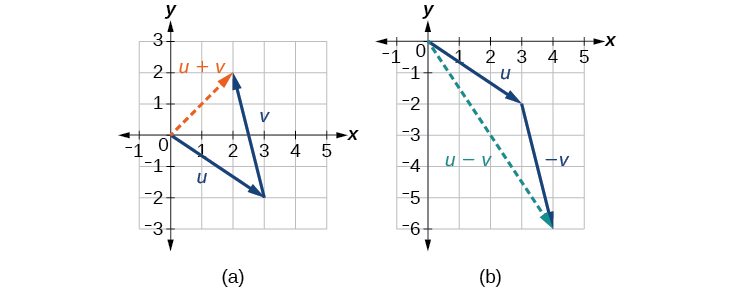
Kielelezo\(\PageIndex{11}\): (a) Jumla ya wadudu wawili (b) Tofauti ya wadudu wawili
Kuzidisha Kwa Scalar
Wakati kuongeza na kuondoa vectors inatupa vector mpya na ukubwa tofauti na mwelekeo, mchakato wa kuzidisha vector kwa scalar, mara kwa mara, mabadiliko tu ukubwa wa vector au urefu wa mstari. Uzidishaji wa Scalar hauna athari juu ya mwelekeo isipokuwa scalar ni hasi, katika hali hiyo mwelekeo wa vector kusababisha ni kinyume na mwelekeo wa vector ya awali.
Kuzidisha kwa scalar kunahusisha bidhaa ya vector na scalar. Kila sehemu ya vector huongezeka kwa scalar. Hivyo, kuzidisha\(v=⟨a,b⟩\) na\(k\), tuna
\(kv=⟨ka,kb⟩\)
Ukubwa tu hubadilika, isipokuwa\(k\) ni hasi, na kisha vector inarudia mwelekeo.
Kutokana vector \(\vec{v}=⟨3,1⟩\), kupata\(3\vec{v}\)\(\dfrac{1}{2}\),, na\(\vec{−v}\).
Suluhisho
Angalia Kielelezo\(\PageIndex{12}\) kwa tafsiri ya kijiometri. Ikiwa\(\vec{v}=⟨3,1⟩\), basi
\[\begin{align*} 3v &= ⟨3⋅3,3⋅1⟩ \\[4pt] &= ⟨9,3⟩ \\[4pt] \dfrac{1}{2}v &= ⟨\dfrac{1}{2}⋅3,\dfrac{1}{2}⋅1⟩ \\[4pt] &=⟨\dfrac{3}{2},\dfrac{1}{2}⟩ \\[4pt] −v &=⟨−3,−1⟩ \end{align*}\]
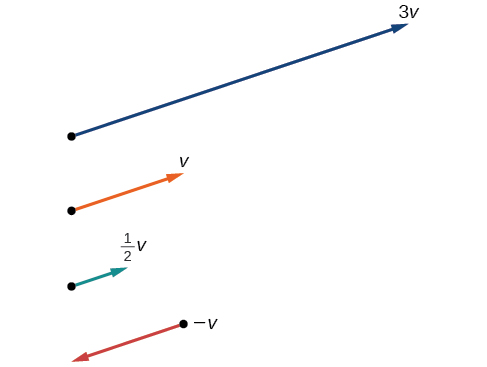
Kielelezo\(\PageIndex{12}\)
Uchambuzi
Kumbuka kwamba vector\(3\vec{v}\) ni mara tatu urefu wa\(\vec{v}\),\(\dfrac{1}{2}\vec{v}\) ni nusu urefu wa\(\vec{v}\), na\(\overrightarrow{–v}\) ni urefu sawa wa\(\vec{v}\), lakini katika mwelekeo kinyume.
Kupata scalar nyingi\(3u\) kupewa\(\vec{u}=⟨5,4⟩\).
- Jibu
-
\(3u=⟨15,12⟩\)
Kupata equation linear kutatua kwa yafuatayo kiasi haijulikani: Nambari moja unazidi idadi nyingine\(17\) na na jumla yao ni\(31\). Kupata namba mbili.
Suluhisho
Kwanza, tunapaswa kuzidisha kila vector kwa scalar.
\[\begin{align*} 3u &= 3⟨3,−2⟩ \\[4pt] &= ⟨9,−6⟩ \\[4pt] 2v &= 2⟨−1,4⟩ \\[4pt] &= ⟨−2,8⟩ \end{align*}\]
Kisha, ongeza mbili pamoja.
\[\begin{align*} w &= 3u+2v \\[4pt] &=⟨9,−6⟩+⟨−2,8⟩ \\[4pt] &= ⟨9−2,−6+8⟩ \\[4pt] &= ⟨7,2⟩ \end{align*}\]
Kwa hiyo,\(w=⟨7,2⟩\).
Kutafuta Fomu ya Kipengele
Katika baadhi ya maombi kuwashirikisha wadudu, ni muhimu kwa sisi kuwa na uwezo wa kuvunja vector chini katika sehemu yake. Vectors zinajumuisha vipengele viwili: sehemu ya usawa ni\(x\) mwelekeo, na sehemu ya wima ni\(y\) mwelekeo. Kwa mfano, tunaweza kuona katika grafu katika Kielelezo\(\PageIndex{13}\) kwamba vector nafasi\(⟨2,3⟩\) linatokana na kuongeza wadudu\(v_1\) na\(v_2\). Tuna\(v_2\) na hatua ya awali\((0,0)\) na uhakika terminal\((2,0)\).
\[\begin{align*} v_1 &= ⟨2−0,0−0⟩ \\[4pt] &= ⟨2,0⟩ \end{align*}\]
Pia tuna\(v_2\) na hatua ya awali\((0,0)\) na hatua ya mwisho\((0, 3)\).
\[\begin{align*} v_2 &= ⟨0−0,3−0⟩ \\[4pt] &= ⟨0,3⟩ \end{align*}\]
Kwa hiyo, vector nafasi ni
\[\begin{align*} v &= ⟨2+0,3+0⟩ \\[4pt] &= ⟨2,3⟩ \end{align*}\]
Kutumia Theorem ya Pythagorean, ukubwa wa\(v_1\) ni\(2\), na ukubwa wa\(v_2\) ni\(3\). Ili kupata ukubwa wa\(v\), tumia formula na vector nafasi.
\[\begin{align*} |v| &= \sqrt{{|v_1|}^2+{|v_2|}^2} \\[4pt] &= \sqrt{2^2+3^2} \\[4pt] &= \sqrt{13} \end{align*}\]
Ukubwa wa\(v\) ni\(\sqrt{13}\). Ili kupata mwelekeo, tunatumia kazi ya tangent\(\tan \theta=\dfrac{y}{x}\).
\[\begin{align*} \tan \theta &= \dfrac{v_2}{v_1} \\[4pt] \tan \theta &= \dfrac{3}{2} \\[4pt] \theta &={\tan}^{−1}\left(\dfrac{3}{2}\right)=56.3° \end{align*}\]
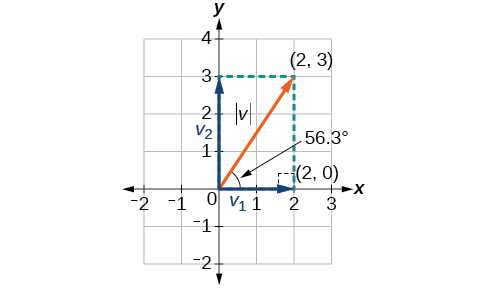
Kielelezo\(\PageIndex{13}\)
Hivyo, ukubwa wa\(\vec{v}\) ni\(\sqrt{13}\) na mwelekeo ni\(56.3^{\circ}\) mbali usawa.
Pata vipengele vya vector \(\vec{v}\)na hatua ya awali\((3,2)\) na hatua ya mwisho\((7,4)\).
Suluhisho
Kwanza kupata nafasi ya kawaida.
\[\begin{align*} v &= ⟨7−3,4−2⟩ \\[4pt] &= ⟨4,2⟩ \end{align*}\]
Angalia mfano katika Kielelezo\(\PageIndex{14}\).
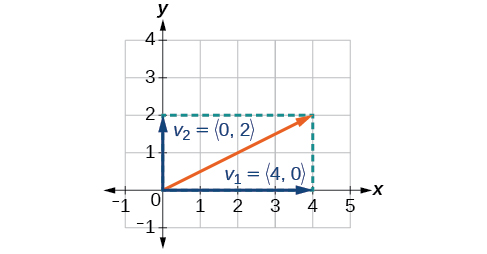
Kielelezo\(\PageIndex{14}\)
Sehemu ya usawa ni\(\vec{v_1}=⟨4,0⟩\) na sehemu ya wima ni\(\vec{v_2}=⟨0,2⟩\).
Kupata Vector Unit katika Mwelekeo wa\(v\)
Mbali na kutafuta vipengele vya vector, ni muhimu pia katika kutatua matatizo ya kupata vector katika mwelekeo sawa na vector iliyotolewa, lakini ya ukubwa\(1\). Tunaita vector na ukubwa wa vector\(1\) kitengo. Tunaweza kisha kuhifadhi mwelekeo wa vector awali wakati kurahisisha mahesabu.
Vectors kitengo hufafanuliwa katika suala la vipengele. Vector ya kitengo cha usawa imeandikwa kama\(\vec{i}=⟨1,0⟩\) na inaelekezwa kwenye mhimili mzuri wa usawa. Vector kitengo cha wima imeandikwa kama\(\vec{j}=⟨0,1⟩\) na inaelekezwa kwenye mhimili mzuri wa wima. Angalia Kielelezo\(\PageIndex{15}\).
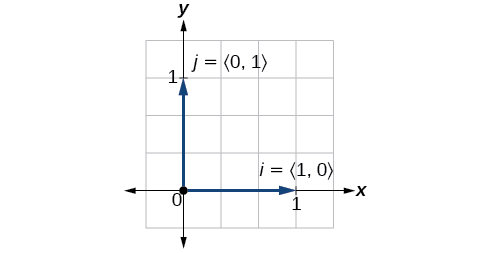
Kielelezo\(\PageIndex{15}\)
Kama \(\vec{v}\)ni nonzero vector, basi\(\dfrac{v}{| v |}\) ni kitengo vector katika mwelekeo wa \(v\). Vector yoyote iliyogawanywa na ukubwa wake ni vector kitengo. Angalia kwamba ukubwa daima ni scalar, na kugawa kwa scalar ni sawa na kuzidisha kwa usawa wa scalar.
Kupata kitengo vector katika mwelekeo sawa na\(v=⟨−5,12⟩\).
Suluhisho
Kwanza, tutapata ukubwa.
\[\begin{align*} |v| &= \sqrt{{(−5)}^2+{(12)}^2} \\[4pt] &= \sqrt{25+144} \\[4pt] &=\sqrt{169} \\[4pt] &= 13 \end{align*}\]
Kisha tunagawanya kila sehemu na\(| v |\), ambayo inatoa vector kitengo katika mwelekeo sawa na\(\vec{v}\):
\(\dfrac{v}{| v |} = −\dfrac{5}{13}i+\dfrac{12}{13}j \)
au, katika fomu ya sehemu
\(\dfrac{v}{| v |}= \left \langle -\dfrac{5}{13},\dfrac{12}{13} \right \rangle\)
Angalia Kielelezo\(\PageIndex{16}\).
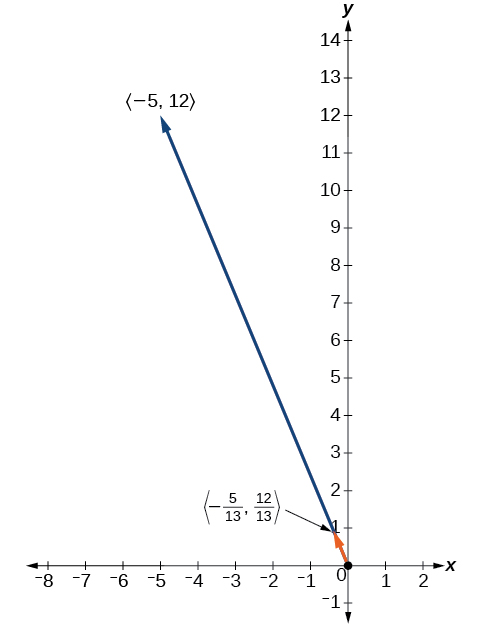
Kielelezo\(\PageIndex{16}\)
Thibitisha kwamba ukubwa wa vector kitengo ni sawa\(1\). Ukubwa wa\(−\dfrac{5}{13}i+\dfrac{12}{13}j\) hutolewa kama
\[\begin{align*} \sqrt{ {\left(−\dfrac{5}{13}\right)}^2+{ \left(\dfrac{12}{13}\right) }^2 } &= \sqrt{\dfrac{25}{169}+\dfrac{144}{169}} \\[4pt] &= \sqrt{\dfrac{169}{169}}\\ &=1 \end{align*}\]
Vector\(u=\dfrac{5}{13}i+\dfrac{12}{13}j\) ni vector kitengo katika mwelekeo sawa na\(v=⟨−5,12⟩\).
Kufanya Operesheni na Vectors katika Masharti\(i\) na\(j\)
Hadi sasa, tumechunguza misingi ya wadudu: ukubwa na mwelekeo, kuongeza vector na kuondoa, kuzidisha scalar, vipengele vya wadudu, na uwakilishi wa wadudu kijiometri. Sasa kwa kuwa tunajua na mikakati ya jumla inayotumiwa katika kufanya kazi na wadudu, tutawakilisha vectors katika kuratibu mstatili kulingana\(i\) na na\(j\).
Kutokana vector\(\vec{v}\) na hatua ya awali\(P=(x_1,y_1)\) na hatua terminal\(Q=(x_2,y_2)\),\(\vec{v}\) imeandikwa kama
\[v=(x_2−x_1)i+(y_1−y_2)j\]
msimamo vector kutoka\((0,0)\) kwa\((a,b)\), wapi\((x_2−x_1)=a\) na\((y_2−y_1)=b\), imeandikwa kama\(\vec{v} = \vec{ai}+ \vec{bj}\). Jumla hii ya vector inaitwa mchanganyiko wa mstari wa vectors\(\vec{i}\) na\(\vec{j}\).
Ukubwa wa\(\vec{v} = \overrightarrow{ai} + \overrightarrow{bj}\) hutolewa kama\(| v |=\sqrt{a^2+b^2}\). Angalia Kielelezo\(\PageIndex{17}\).
.jpg)
Kielelezo\(\PageIndex{17}\)
Kutokana na vector\(\vec{v}\) na hatua ya awali\(P=(2,−6)\) na hatua ya mwisho\(Q=(−6,6)\), andika vector kwa suala la\(\vec{i}\) na\(\vec{j}\).
Suluhisho
Anza kwa kuandika fomu ya jumla ya vector. Kisha kuchukua nafasi ya kuratibu na maadili yaliyotolewa.
\[\begin{align*} v &= (x_2−x_1)i+(y_2−y_1)j \\[4pt] &=(−6−2)i+(6−(−6))j \\[4pt] &= −8i+12j \end{align*}\]
Kutokana\(P_1=(−1,3)\) na hatua ya awali na hatua ya mwisho\(P_2=(2,7)\), andika vector\(\vec{v}\) kwa suala la\(\vec{i}\) na\(\vec{j}\).
Suluhisho
Anza kwa kuandika fomu ya jumla ya vector. Kisha kuchukua nafasi ya kuratibu na maadili yaliyotolewa.
\[\begin{align*} v &= (x_2−x_1)i+(y_2−y_1)j \\[4pt] v &= (2−(−1))i+(7−3)j \\[4pt] &= 3i+4j \end{align*}\]
Andika vector\(\vec{u}\) na hatua ya awali\(P=(−1,6)\) na hatua ya mwisho\(Q=(7,−5)\) kwa mujibu wa\(\vec{i}\) na\(\vec{j}\).
- Jibu
-
\(u=8i−11j\)
Kufanya Operesheni ya Vectors katika Masharti\(i\) na\(j\)
Wakati vectors imeandikwa kwa suala la\(i\) na\(j\), tunaweza kufanya kuongeza, kuondoa, na kuzidisha scalar kwa kufanya shughuli kwenye vipengele vinavyolingana.
Kutokana\(v = ai + bj\) na\(u = ci + dj\), basi
\[\begin{align*} v+u &= (a+c)i+(b+d)j \\[4pt] v−u &= (a−c)i+(b−d)j \end{align*}\]
Kupata jumla ya\(v_1=2i−3j\) na\(v_2=4i+5j\).
Suluhisho
\[\begin{align*} v_1+v_2 &= (2+4)i+(−3+5)j \\[4pt] &= 6i+2j \end{align*}\]
Kuhesabu Fomu ya Kipengele cha Vector: Mwelekeo
Tumeona jinsi ya kuteka wadudu kulingana na pointi zao za awali na za mwisho na jinsi ya kupata vector nafasi. Sisi pia kuchunguza nukuu kwa wadudu inayotolewa hasa katika Cartesian kuratibu ndege kwa kutumia\(i\) na\(j\). Kwa yoyote ya wadudu hawa, tunaweza kuhesabu ukubwa. Sasa, tunataka kuchanganya pointi muhimu, na kuangalia zaidi katika mawazo ya ukubwa na mwelekeo.
Kuhesabu mwelekeo ifuatavyo mchakato huo wa moja kwa moja tulitumia kwa kuratibu polar. Tunapata mwelekeo wa vector kwa kutafuta angle kwa usawa. Tunafanya hivyo kwa kutumia utambulisho wa msingi wa trigonometric, lakini kwa\(| v |\) kuchukua nafasi\(r\).
Kutokana na vector nafasi\(v=⟨x,y⟩\) na angle mwelekeo\(\theta\),
\[ \begin{align*} \cos \theta &= \dfrac{x}{|v|} \text{ and } \sin \theta=y|v| \\[4pt] x &= |v| \cos \theta \\[4pt] y &= |v| \sin \theta \end{align*}\]
Hivyo,\(v=xi+yj=| v | \cos \theta i+| v | \sin \theta j\), na ukubwa unaonyeshwa kama\(| v |=\sqrt{x^2+y^2}\).
Andika vector kwa urefu kwa\(7\) pembe ya\(135°\) chanya x -axis kwa suala la ukubwa na mwelekeo.
Suluhisho
Kutumia formula uongofu\(x=| v | \cos \theta i\) na\(y=| v | \sin \theta j\), tunaona kwamba
\[ \begin{align*} x &= 7\cos(135°)i \\[4pt] &= −\dfrac{7\sqrt{2}}{2} \\[4pt] y &=7 \sin(135°)j \\[4pt] &= \dfrac{7\sqrt{2}}{2} \end{align*}\]
Vector hii inaweza kuandikwa kama\(v=7\cos(135°)i+7\sin(135°)j\) au kilichorahisishwa kama
\(v=−\dfrac{7\sqrt{2}}{2}i+\dfrac{7\sqrt{2}}{2}j\)
Vector husafiri kutoka asili hadi hatua\((3,5)\). Andika vector kwa suala la ukubwa na mwelekeo.
- Jibu
-
\(v=\sqrt{34}\cos(59°)i+\sqrt{34}\sin(59°)j\)
Ukubwa =\(34\)
\(\theta={\tan}^{−1}\left(\dfrac{5}{3}\right)=59.04°\)
Kutafuta Bidhaa ya Dot ya Vectors Mbili
Kama tulivyojadiliwa mapema katika sehemu hiyo, kuzidisha kwa scalar kunahusisha kuzidisha vector kwa scalar, na matokeo ni vector. Kama tulivyoona, kuzidisha vector kwa idadi inaitwa kuzidisha scalar. Ikiwa tunazidisha vector kwa vector, kuna uwezekano mawili: bidhaa ya dot na bidhaa ya msalaba. Sisi tu kuchunguza dot bidhaa hapa; unaweza kukutana bidhaa msalaba katika kozi ya juu zaidi hisabati.
Bidhaa ya dot ya vectors mbili inahusisha kuzidisha vectors mbili pamoja, na matokeo ni scalar.
Bidhaa ya dot ya vectors mbili\(v=⟨a,b⟩\) na\(u=⟨c,d⟩\) ni jumla ya bidhaa ya vipengele vya usawa na bidhaa ya vipengele vya wima.
\[v⋅u=ac+bd\]
Ili kupata angle kati ya vectors mbili, tumia formula hapa chini.
\[\cos \theta=\dfrac{v}{| v |}⋅\dfrac{u}{| u |}\]
Kupata dot bidhaa ya\(v=⟨5,12⟩\) na\(u=⟨−3,4⟩\).
Suluhisho
Kutumia formula, tuna
\[\begin{align*} v⋅u &= ⟨5,12⟩⋅⟨−3,4⟩ \\[4pt] &= 5⋅(−3)+12⋅4 \\[4pt] &= −15+48 \\[4pt] &= 33 \end{align*}\]
Kupata dot bidhaa ya\(v_1 = 5i + 2j\) na\(v_2 = 3i + 7j\). Kisha, tafuta angle kati ya vectors mbili.
Suluhisho
Kutafuta bidhaa ya dot, tunazidisha vipengele vinavyolingana.
\[ \begin{align*} v_1⋅v_2 &= ⟨5,2⟩⋅⟨3,7⟩ \\[4pt] &= 5⋅3+2⋅7 \\[4pt] &= 15+14 \\[4pt] &= 29 \end{align*}\]
Ili kupata angle kati yao, tunatumia formula\(\cos \theta=\dfrac{v}{|v|}⋅\dfrac{u}{|u|}\).
\[\begin{align*} \dfrac{v}{|v|}\cdot \dfrac{u}{|u|} &= \left \langle \dfrac{5}{\sqrt{29}}+\dfrac{2}{\sqrt{29}} \right \rangle \cdot \left \langle \dfrac{3}{\sqrt{58}}+\dfrac{7}{\sqrt{58}} \right \rangle \\[4pt] &=\dfrac{5}{\sqrt{29}}\cdot \dfrac{3}{\sqrt{58}}+\dfrac{2}{\sqrt{29}}\cdot \dfrac{7}{\sqrt{58}} \\[4pt] &= \dfrac{15}{\sqrt{1682}}+\dfrac{14}{\sqrt{1682}}\\ &=\dfrac{29}{\sqrt{1682}} \\[4pt] &= 0.707107 \\[4pt] {\cos}^{-1}(0.707107) &= 45° \end{align*}\]
Angalia Kielelezo\(\PageIndex{18}\).
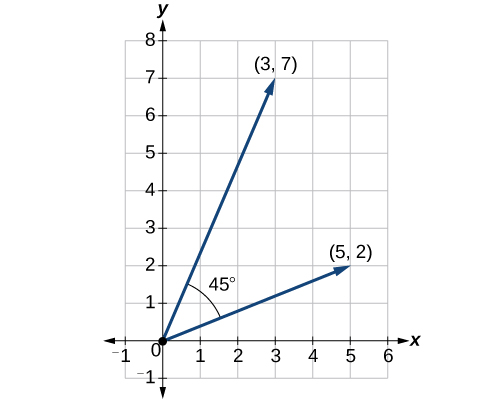
Kielelezo\(\PageIndex{18}\)
Pata angle kati\(u=⟨−3,4⟩\) na\(v=⟨5,12⟩\).
Suluhisho
Kutumia formula, tuna
\[\begin{align*} \theta &= {\cos}^{−1}\left(\dfrac{u}{|u|}⋅\dfrac{v}{|v|}\right) \\[4pt] \left(\dfrac{u}{|u|}⋅\dfrac{v}{|v|}\right) &= \dfrac{−3i+4j}{5}⋅\dfrac{5i+12j}{13} \\[4pt] &= \left(− \dfrac{3}{5}⋅ \dfrac{5}{13}\right)+\left(\dfrac{4}{5}⋅ \dfrac{12}{13}\right) \\[4pt] &= −\dfrac{15}{65}+\dfrac{48}{65} \\[4pt] &= \dfrac{33}{65} \\[4pt] \theta &= {\cos}^{−1}\left(\dfrac{33}{65}\right) \\[4pt] &= 59.5^{\circ} \end{align*}\]
Angalia Kielelezo\(\PageIndex{19}\).
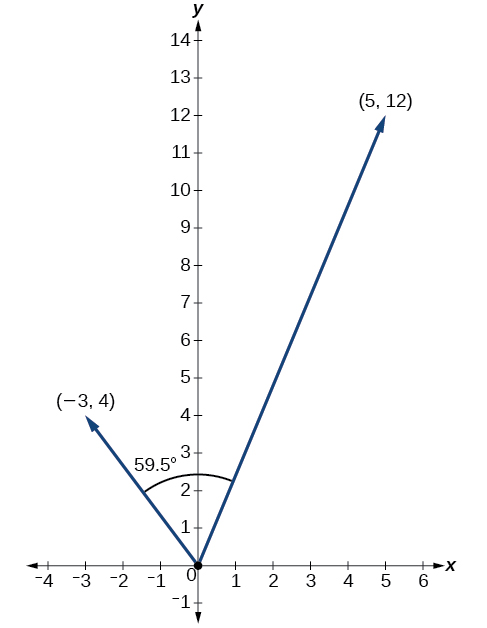
Kielelezo\(\PageIndex{19}\)
Sasa tuna zana za kutatua tatizo tuliloletwa katika ufunguzi wa sehemu hiyo.
ndege ni flying katika airspeed ya\(200\) maili kwa saa inaongozwa juu ya kuzaa SE ya\(140°\). Upepo wa kaskazini (kutoka kaskazini hadi kusini) unapiga\(16.2\) maili kwa saa. Je! Kasi ya ardhi na kuzaa halisi ya ndege ni nini? Angalia Kielelezo\(\PageIndex{20}\).
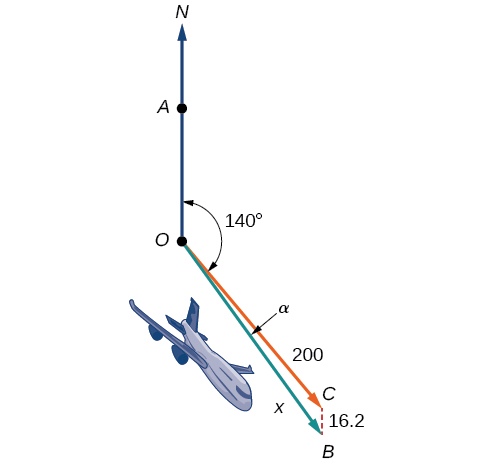
Kielelezo\(\PageIndex{20}\)
Suluhisho
Kasi ya ardhi\(x\) inawakilishwa na mchoro, na tunahitaji kupata angle\(\alpha\) ili kuhesabu kuzaa kubadilishwa, ambayo itakuwa\(140°+\alpha\).
Taarifa katika Kielelezo\(\PageIndex{20}\), kwamba angle\(\angle BCO\) lazima kuwa sawa na angle\(\angle AOC\) na utawala wa pembe alternating mambo ya ndani, hivyo angle\(\angle BCO\) ni 140°. Tunaweza kupata\(x\) kwa Sheria ya Cosines:
\[\begin{align*} x^2 &= {(16.2)}^2+{(200)}^2−2(16.2)(200) \cos(140°) \\[4pt] x^2 &= 45,226.41 \\[4pt] x &= \sqrt{45,226.41} \\[4pt] x &= 212.7 \end{align*}\]
Kasi ya ardhi ni takriban\(213\) maili kwa saa. Sasa tunaweza kuhesabu kuzaa kwa kutumia Sheria ya Sines.
\[\begin{align*} \dfrac{\sin \alpha}{16.2} &= \dfrac{\sin(140°)}{212.7} \\[4pt] \sin \alpha &= \dfrac{16.2 \sin(140°)}{212.7} \\[4pt] &=0.04896 \\[4pt] {\sin}^{−1}(0.04896) &= 2.8° \end{align*}\]
Kwa hiyo, ndege ina SE kuzaa ya\(140°+2.8°=142.8°\). Kasi ya ardhi ni\(212.7\) maili kwa saa.
Key Concepts
- The position vector has its initial point at the origin. See Example \(\PageIndex{1}\).
- If the position vector is the same for two vectors, they are equal. See Example \(\PageIndex{2}\).
- Vectors are defined by their magnitude and direction. See Example \(\PageIndex{3}\).
- If two vectors have the same magnitude and direction, they are equal. See Example \(\PageIndex{4}\).
- Vector addition and subtraction result in a new vector found by adding or subtracting corresponding elements. See Example \(\PageIndex{5}\).
- Scalar multiplication is multiplying a vector by a constant. Only the magnitude changes; the direction stays the same. See Example \(\PageIndex{6}\) and Example \(\PageIndex{7}\).
- Vectors are comprised of two components: the horizontal component along the positive \(x\)-axis, and the vertical component along the positive \(y\)-axis. See Example \(\PageIndex{8}\).
- The unit vector in the same direction of any nonzero vector is found by dividing the vector by its magnitude.
- The magnitude of a vector in the rectangular coordinate system is \(| v |=\sqrt{a^2+b^2}\). See Example \(\PageIndex{9}\).
- In the rectangular coordinate system, unit vectors may be represented in terms of \(ii\) and \(jj\) where \(i\) represents the horizontal component and \(j\) represents the vertical component. Then, \(v = ai + bj\) is a scalar multiple of \(v\) by real numbers \(a\) and \(b\). See Example \(\PageIndex{10}\) and Example \(\PageIndex{11}\).
- Adding and subtracting vectors in terms of \(i\) and \(j\) consists of adding or subtracting corresponding coefficients of \(i\) and corresponding coefficients of \(j\). See Example \(\PageIndex{12}\).
- A vector \(v = ai + bj\) is written in terms of magnitude and direction as \(v=| v |\cos \theta i+| v |\sin \theta j\). See Example \(\PageIndex{13}\).
- The dot product of two vectors is the product of the \(i\) terms plus the product of the \(j\) terms. See Example \(\PageIndex{14}\).
- We can use the dot product to find the angle between two vectors. Example \(\PageIndex{15}\) and Example \(\PageIndex{16}\).
- Dot products are useful for many types of physics applications. See Example \(\PageIndex{17}\).


