12.4: Sheria za Kiwango cha Jumuishi

Malengo ya kujifunza

• Eleza fomu na kazi ya sheria jumuishi kiwango
• Kufanya mahesabu ya sheria ya kiwango cha jumuishi kwa athari za sifuri, za kwanza, na za pili
• Eleza nusu ya maisha na kufanya mahesabu yanayohusiana
• Tambua utaratibu wa mmenyuko kutoka kwa mkusanyiko wa data/wakati

Sheria za kiwango ambacho tumeona hadi sasa zinahusiana na kiwango na viwango vya reactants. Tunaweza pia kuamua aina ya pili ya kila sheria kiwango kwamba inahusiana viwango vya reactants na wakati. Hizi huitwa sheria jumuishi kiwango. Tunaweza kutumia sheria ya kiwango cha jumuishi ili kuamua kiasi cha reactant au bidhaa zilizopo baada ya kipindi cha muda au kukadiria muda unaohitajika kwa mmenyuko kuendelea kwa kiwango fulani. Kwa mfano, sheria ya kiwango cha jumuishi hutumiwa kuamua urefu wa muda nyenzo za mionzi lazima zihifadhiwe kwa radioactivity yake kuoza kwa kiwango salama.

Kutumia calculus, sheria ya kiwango cha tofauti kwa mmenyuko wa kemikali inaweza kuunganishwa kwa heshima na wakati wa kutoa equation inayohusiana na kiasi cha reactant au bidhaa zilizopo katika mchanganyiko wa majibu kwa muda uliopita wa mmenyuko. Utaratibu huu unaweza kuwa moja kwa moja au ngumu sana, kulingana na utata wa sheria ya kiwango cha tofauti. Kwa madhumuni ya majadiliano, tutazingatia sheria zinazosababisha kiwango cha jumuishi kwa athari za kwanza, za pili, na zero.

Athari ya Kwanza

Equation inayohusiana na kiwango cha mara$k$ kwa mara$[A]_0$ na mkusanyiko wa awali na mkusanyiko wa$[A]_t$ sasa baada ya muda wowote$t$ unaweza kupatikana kwa mmenyuko wa kwanza na umeonyeshwa kuwa:

$$\ln\left(\dfrac{[A]_t}{[A]_0}\right)=−kt \nonumber$$

au kwa njia nyingine

$$\ln\left(\dfrac{[A]_0}{[A]_t}\right)=kt \nonumber$$

au

$$[A]=[A]_0e^{−kt} \nonumber$$

Mfano$\PageIndex{1}$: The Integrated Rate Law for a First-Order Reaction

Kiwango cha mara kwa mara kwa utengano wa kwanza wa cyclobutane,$\ce{C4H8}$ saa 500 °C ni 9.2 × 10 ^{˚ -3} s ^-1:

$$\ce{C4H8⟶2C2H4} \nonumber$$

Itachukua muda gani kwa 80.0% ya sampuli ya C ₄ H ₈ ili kuharibika?

Suluhisho

Tunatumia fomu jumuishi ya sheria ya kiwango kujibu maswali kuhusu muda:

$$\ln\left(\dfrac{[A]_0}{[A]}\right)=kt \nonumber$$

Kuna vigezo vinne katika sheria ya kiwango, hivyo kama tunajua tatu kati yao, tunaweza kuamua nne. Katika kesi hii tunajua [A] ₀, [A], na k, na haja ya kupata t.

Mkusanyiko wa awali wa C ₄ H ₈, [A] ₀, hautolewa, lakini utoaji ambao 80.0% ya sampuli imeharibika ni habari za kutosha kutatua tatizo hili. Hebu x kuwa mkusanyiko wa awali, katika kesi hiyo ukolezi baada ya kuharibika kwa 80.0% ni 20.0% ya x au 0.200 x Kurekebisha sheria ya kiwango ili kutenganisha t na kubadilisha kiasi kilichotolewa mavuno:

\ [kuanza {align*}
t&=\ ln\ dfrac {[x]} {[0.200x]} ×\ drac {1} {k}\\ [4pt]
&=\ mathrm {\ ln\ drac {0.100\ :mol\: L^ {0.100\: mol\: L^ {-1}} frac {1} {9.2×10^ {˚ 3}\: s^ {-1}}}\\ [4pt]
&=\ hesabu {1.609×\ drac {1} {9.2×10^ {˚ 3}\ :s^ {-1}}}\\ [4pt]
&=\ hesabu {1.7×10^ 2\: s}
\ mwisho {align*}\ nonumber\]

Zoezi$\PageIndex{1}$

Iodini-131 ni isotopu ya mionzi ambayo hutumiwa kutambua na kutibu aina fulani za saratani ya tezi. Iodini-131 huharibika kwa xenon-131 kulingana na equation:

$$\textrm{I-131 ⟶ Xe-131 + electron} \nonumber$$

Kuoza ni utaratibu wa kwanza na kiwango cha mara kwa mara cha 0.138 ^{d -1}. Uozo wote wa mionzi ni utaratibu wa kwanza. Ni siku ngapi itachukua 90% ya iodini-131 katika ufumbuzi wa 0.500 M wa dutu hii kuoza kwa Xe-131?

Jibu

siku 16.7

Tunaweza kutumia sheria jumuishi kiwango na data ya majaribio kwamba wajumbe wa muda na mkusanyiko habari kuamua utaratibu na kiwango mara kwa mara ya majibu. Sheria ya kiwango cha jumuishi inaweza kupangwa upya kwa muundo wa kawaida wa usawa wa mstari:

\ [kuanza {align}
\ ln [A] & =( -k) (t) +\ ln [A] _0\ studio {in1st}\\ [4pt]
y&=mx+b
\ mwisho {align}\ nonumber\]

Mpango wa$\ln[A]$ dhidi$t$ ya mmenyuko wa kwanza ni mstari wa moja kwa moja na mteremko wa$−k$ na kupinga$\ln[A]_0$. Ikiwa seti ya data ya kiwango imepangwa kwa mtindo huu lakini haitoi mstari wa moja kwa moja, majibu hayatoi utaratibu wa kwanza$A$.

Mfano$\PageIndex{2}$: Determination of Reaction Order by Graphing

Onyesha kwamba data katika Kielelezo hii inaweza kuwakilishwa na sheria ya kwanza ili kiwango kwa graphing ln [H ₂ O ₂] dhidi ya muda. Kuamua kiwango cha mara kwa mara kwa kiwango cha kuharibika kwa H ₂ O ₂ kutoka data hii.

Suluhisho

Takwimu kutoka kwa Kielelezo hiki na kuongeza maadili ya ln [H ₂ O ₂] hutolewa katika Kielelezo$\PageIndex{1}$.

Kielelezo$\PageIndex{1}$: Uhusiano wa mstari kati ya ln [H _{2 O 2}] na wakati unaonyesha kwamba kuharibika kwa peroxide ya hidrojeni ni mmenyuko wa kwanza.

Ufumbuzi wa Mfano 12.4.2

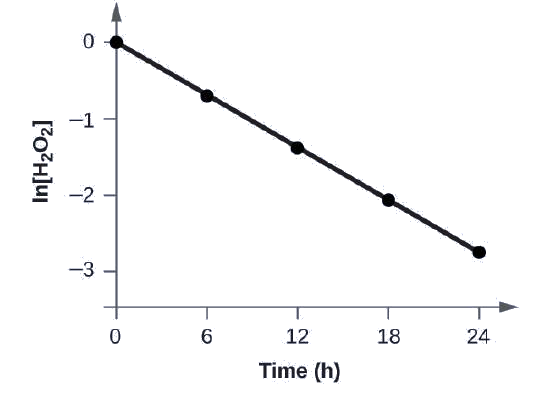
Jaribio	Muda (h)	[H 2 O 2] (M)	ln [H 2 L 2]
1	0	1.000	0.0
2	6.00	0.500	-0.693
3	12.00	0.250	-1.386
4	18.00	0.125	-2.079
5	24.00	0.0625	-2.772

Mpango wa ln [H ₂ O ₂] dhidi ya muda ni mstari, kwa hiyo tumehakikishia kuwa majibu yanaweza kuelezewa na sheria ya kiwango cha kwanza.

Kiwango cha mara kwa mara kwa mmenyuko wa kwanza ni sawa na hasi ya mteremko wa njama ya ln [H ₂ O ₂] dhidi ya wakati ambapo:

$$\ce{slope}=\dfrac{\textrm{change in }y}{\textrm{change in }x}=\dfrac{Δy}{Δx}=\dfrac{Δ\ln[\ce{H2O2}]}{Δt} \nonumber$$

Ili kuamua mteremko wa mstari, tunahitaji maadili mawili ya ln [H ₂ O ₂] kwa maadili tofauti ya t (moja karibu na kila mwisho wa mstari ni bora). Kwa mfano, thamani ya ln [H ₂ O ₂] wakati t ni 6.00 h ni -0.693; thamani wakati t = 12.00 h ni -1.386:

\ [kuanza {align*}
\ ce {mteremko} &=\ hesabu {\ dfrac {-1.386—( -0.693)} {12.00\: h-6.00\: h}\\ [4pt]
&=\ hesabu {\ dfrac {-0.693} {6.00\: h}}\\ [4pt]
&=\ mathrm {-1.155×10^ {ї 2}\ :h^ {,11}}\\ [4pt]
k&=\ mathrm {-mteremko =⸺- (-1.155×10^ {—1}\ h^ {,11}) =1.155×10^ {˚ 1}\ h^ {˚ 1} }
\ mwisho {align*}\ nonumber\]

Zoezi$\PageIndex{2}$

Grafu data zifuatazo ili uone kama mmenyuko$A⟶B+C$ ni utaratibu wa kwanza.

Takwimu kwa majibu$A⟶B+C$

Jaribio	Muda (s)	[A]
1	4.0	0.220
2	8.0	0.144
3	12.0	0.110
4	16.0	0.088
5	20.0	0.074

Jibu

Mpango wa ln [A] vs. t si mstari wa moja kwa moja. equation si amri ya kwanza:

 

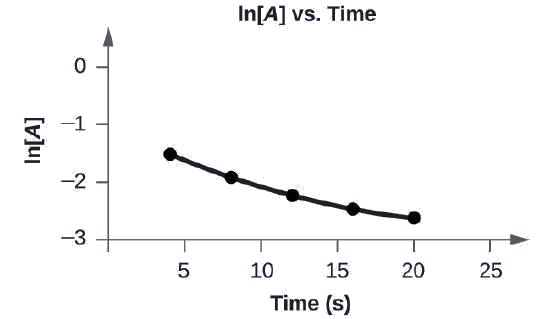
Grafu, iliyoandikwa hapo juu kama “l n [A] vs Muda” inavyoonyeshwa. Mhimili wa x umeandikwa, “Muda (s)” na mhimili wa y umeandikwa, “l n [A].” Mhimili wa x unaonyesha alama saa 5, 10, 15, 20, na masaa 25. Mhimili wa y unaonyesha alama katika hasi 3, hasi 2, hasi 1, na 0. Curve kidogo hutolewa kuunganisha pointi tano kwenye kuratibu za takriban (4, hasi 1.5), (8, hasi 2), (12, hasi 2.2), (16, hasi 2.4), na (20, hasi 2.6).

 

Pili ili Athari

Ulinganisho unaohusiana na viwango vya reactants na kiwango cha mara kwa mara cha athari za pili ni ngumu sana. Tutajizuia kwa athari rahisi ya pili, yaani, wale walio na viwango ambavyo vinategemea mkusanyiko mmoja tu wa reactant na ilivyoelezwa na sheria ya kiwango cha tofauti:

$$\ce{Rate}=k[A]^2 \nonumber$$

Kwa athari hizi za pili, sheria ya kiwango cha jumuishi ni:

$$\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \label{int2nd}$$

ambapo maneno katika equation yana maana yake ya kawaida kama ilivyoelezwa mapema.

Mfano$\PageIndex{3}$: The Integrated Rate Law for a Second-Order Reaction

Majibu ya gesi ya butadiene (C ₄ H ₆) yenyewe hutoa gesi C ₈ H ₁₂ kama ifuatavyo:

$$\ce{2C4H6}(g)⟶\ce{C8H12(g)} \nonumber$$

Mmenyuko ni utaratibu wa pili na kiwango cha mara kwa mara sawa na 5.76 × 10 ^{÷ 2} L/mol/min chini ya hali fulani. Ikiwa mkusanyiko wa awali wa butadiene ni 0.200 M, ni mkusanyiko gani uliobaki baada ya dakika 10.0?

Suluhisho

Tunatumia fomu jumuishi ya sheria ya kiwango kujibu maswali kuhusu wakati. Kwa mmenyuko wa pili, tuna:

$$\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \nonumber$$

Tunajua vigezo vitatu katika equation hii: [A] ₀ = 0.200 Mol/L, k = 5.76 × 10 ^{-1 -2} L/mol/min, na t = 10.0 min. Kwa hiyo, tunaweza kutatua kwa [A], variable ya nne:

\ [kuanza {align*}
\ dfrac {1} {[A]} &=\ hesabu {(5.76×10^ {¯ 2}\: L\: mol^ {-1}\ :min^ {-1}) (10\ :min) +\ dfrac {1} {0.200\ :mol^ {-1}}}\\ [4pt]
\ dfrac {1} {[A]} &=\ hesabu {(5.76×10^ {-1}\: L\: Mol^ {˚ 1}) +5.00\: L\: Mol^ {-1}}\ [4pt]
\\ drac {1} {[A]} &=\ hesabu {5.58\ L\: Mol^ {-1}}\\ 4pt]
[A] &=\ hisabati {1.79×10^ {-1}\ :mol\: L ^ {˚ 1}}
\ mwisho {align*}\ hakuna nambari\]

Kwa hiyo 0.179 mol/L ya butadiene kubaki mwishoni mwa 10.0 min, ikilinganishwa na 0.200 mol/L ambayo awali ilikuwa sasa.

Zoezi$\PageIndex{3}$

Ikiwa mkusanyiko wa awali wa butadiene ni 0.0200 M, ni mkusanyiko gani uliobaki baada ya 20.0 min?

Jibu

0.0196 mol/L

Sheria ya kiwango cha jumuishi kwa athari zetu za pili zina aina ya usawa wa mstari wa moja kwa moja:

\ [kuanza {align*}
\ dfrac {1} {[A]} &=kt+\ dfrac {1} {[A] _0}\ [4pt]
y&=mx+b
\ mwisho {align*}\ nonumber\]

Mpango wa$\dfrac{1}{[A]}$ dhidi ya t kwa mmenyuko wa pili ni mstari wa moja kwa moja na mteremko wa k na kupinga$\dfrac{1}{[A]_0}$. Ikiwa njama sio mstari wa moja kwa moja, basi majibu sio utaratibu wa pili.

Mfano$\PageIndex{4}$: Determination of Reaction Order by Graphing

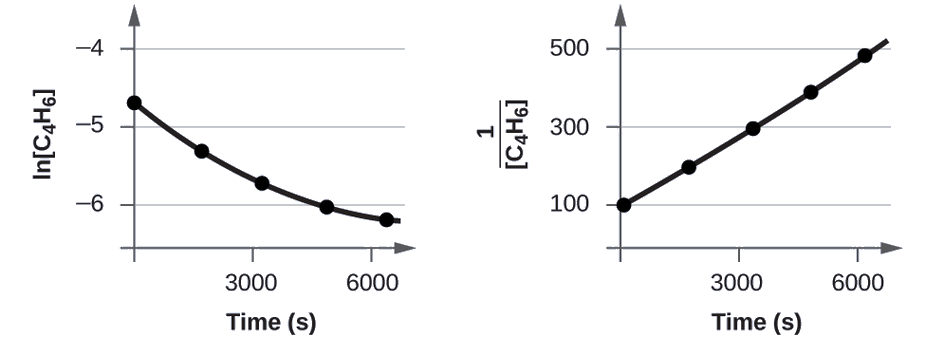
Jaribu data iliyotolewa ili kuonyesha kama dimerization ya C ₄ H ₆ ni majibu ya kwanza au ya pili.

Suluhisho

Ufumbuzi wa Mfano 12.4.4

Jaribio	Muda (s)	[C 4 H 6] (M)
1	0	1.00 × 10 ^-1 -2
2	1600	5.04 × ^10 -3
3	3200	3.37 × ^10 -3
4	4800	2.53 × ^10 -3
5	6200	2.08 × ^10 -3

Ili kutofautisha majibu ya kwanza kutoka kwa mmenyuko wa pili, tunapanga njama ln [C ₄ H ₆] dhidi ya t na kulinganisha na njama$\mathrm{\dfrac{1}{[C_4H_6]}}$ dhidi ya t. Maadili yanahitajika kwa viwanja hivi yanafuata.

Ufumbuzi wa Mfano 12.4.4

Muda (s)	$\dfrac{1}{[\ce{C4H6}]}\:(M^{−1})$	ln [C 4 H 6]
0	\ (\ dfrac {1} {\ ce {C4H6}]]}\: (M^ {˚ 1})\)” style="text-align:katikati; "> 100	-4.605
1600	\ (\ dfrac {1} {\ ce {C4H6}]]}\: (M^ {˚ 1})\)” style="text-align:katikati; "> 198	-5.289
3200	\ (\ dfrac {1} {\ ce {C4H6}]]}\: (M^ {˚ 1})\)” style="text-align:katikati; "> 296	-5.692
4800	\ (\ dfrac {1} {\ ce {C4H6}]]}\: (M^ {˚ 1})\)” style="Nakala-align:katikati; "> 395	-5.978
6200	\ (\ dfrac {1} {\ ce {C4H6}]]}\: (M^ {˚ 1})\)” style="Nakala-align:katikati; "> 481	-6.175

Viwanja vinaonyeshwa kwenye Kielelezo$\PageIndex{2}$. Kama unaweza kuona, njama ya ln [C ₄ H ₆] dhidi ya t sio mstari, kwa hiyo majibu sio utaratibu wa kwanza. Mpango wa$\dfrac{1}{[\ce{C4H6}]}$ dhidi ya t ni mstari, unaonyesha kwamba mmenyuko ni utaratibu wa pili.

Kielelezo$\PageIndex{2}$: Grafu hizi mbili zinaonyesha viwanja vya kwanza na vya pili vya dimerization ya C ₄ H ₆. Kwa kuwa njama ya kwanza (kushoto) sio mstari, tunajua kwamba majibu sio utaratibu wa kwanza. Mwelekeo wa mstari katika njama ya pili (kulia) inaonyesha kwamba mmenyuko hufuata kinetics ya pili.

Grafu mbili zinaonyeshwa, kila mmoja ana lebo “Muda (s)” kwenye mhimili wa x. Grafu upande wa kushoto imeandikwa, “l n [C subscript 4 H subscript 6],” kwenye mhimili wa y. Grafu upande wa kulia imeandikwa “1 imegawanywa na [C subscript 4 H subscript 6],” kwenye mhimili wa y. X-axes kwa grafu zote mbili zinaonyesha alama saa 3000 na 6000. Mhimili wa y kwa grafu upande wa kushoto unaonyesha alama kwenye hasi 6, hasi 5, na hasi 4. Kupungua kidogo concave up Curve ni inayotolewa kwa njia ya pointi tano katika kuratibu yaani (0, hasi 4.605), (1600, hasi 5.289), (3200, hasi 5.692), (4800, hasi 5.978), na (6200, hasi 6.175). Mhimili wa y kwa grafu upande wa kulia unaonyesha alama kwenye 100, 300, na 500. Curve takriban linear kuongeza ni inayotolewa kupitia pointi tano katika kuratibu yaani (0, 100), (1600, 198), (3200, 296), na (4800, 395), na (6200, 481).

Zoezi$\PageIndex{4}$

Je, data zifuatazo zinafaa sheria ya kiwango cha pili?

Takwimu kwa sheria ya kiwango cha pili

Jaribio	Muda (s)	[A] (M)
1	5	0.952
2	10	0.625
3	15	0.465
4	20	0.370
5	25	0.308
6	35	0.230

 

Jibu

Ndiyo. Mpango wa$\dfrac{1}{[A]}$ vs. t ni mstari:

 

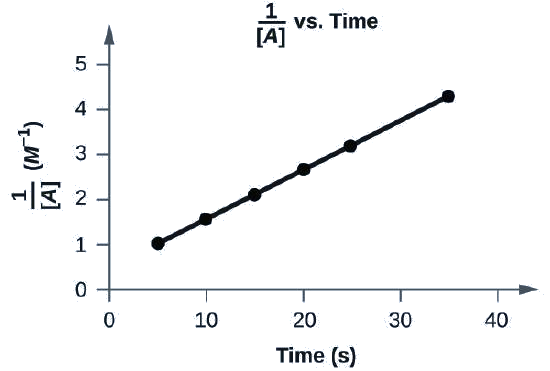
Grafu, yenye kichwa “1 imegawanywa na [A] dhidi ya Muda” inavyoonyeshwa, na lebo, “Muda (s),” kwenye x-axis. Lebo “1 iliyogawanywa na [A]” inaonekana kushoto ya mhimili wa y. Mhimili wa x unaonyesha alama zinazoanza sifuri na kuendelea kwa vipindi vya 10 hadi na ikiwa ni pamoja na 40. Mhimili wa y upande wa kushoto unaonyesha alama zinazoanza saa 0 na kuongezeka kwa vipindi vya 1 hadi na ikiwa ni pamoja na 5. Mstari na mwenendo unaoongezeka hutolewa kupitia pointi sita kwa takriban (4, 1), (10, 1.5), (15, 2.2), (20, 2.8), (26, 3.4), na (36, 4.4).

 

Zero Order Athari

Kwa athari za utaratibu wa sifuri, sheria ya kiwango cha tofauti ni:

$$\ce{Rate}=k[A]^0=k \nonumber$$

Kwa hiyo mmenyuko wa sifuri huonyesha kiwango cha majibu ya mara kwa mara, bila kujali mkusanyiko wa majibu yake.

Sheria ya kiwango cha jumuishi kwa mmenyuko wa sifuri pia ina fomu ya usawa wa mstari wa moja kwa moja:

\ [\ kuanza {align*}
[A] &=18-kt+ [A] _0\ studio {intzero}\\ [4pt]
y&=mx+b
\ mwisho {align*}\ nonumber\]

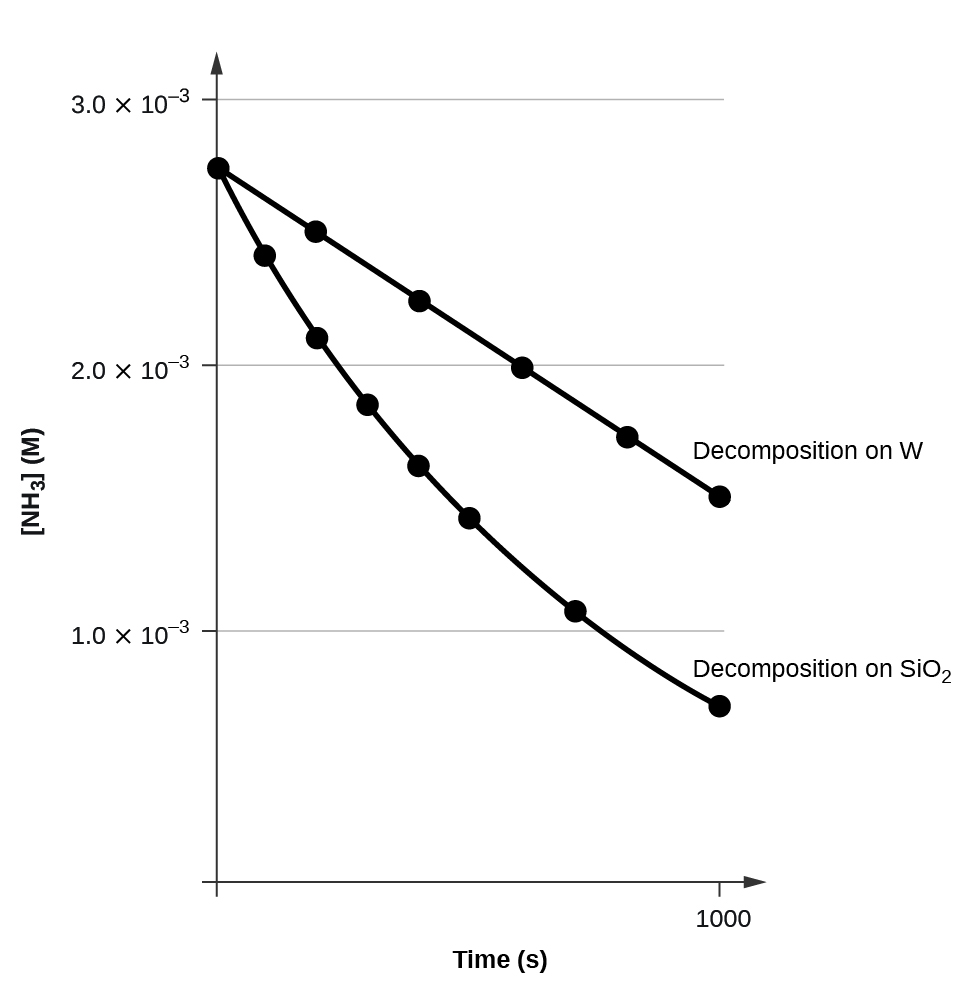
Mpango wa$[A]$ dhidi$t$ ya mmenyuko wa mpangilio wa sifuri ni mstari wa moja kwa moja na mteremko wa -k na kizuizi cha [A] ₀. Kielelezo$\PageIndex{3}$ kinaonyesha njama ya [NH ₃] dhidi ya t kwa kuharibika kwa amonia kwenye waya wa moto wa tungsten na kwa kuharibika kwa amonia kwenye quartz ya moto (_{SiO 2}). Uharibifu wa NH ₃ kwenye tungsten ya moto ni utaratibu wa sifuri; njama ni mstari wa moja kwa moja. Uharibifu wa NH ₃ kwenye quartz ya moto sio utaratibu wa sifuri (ni amri ya kwanza). Kutoka kwenye mteremko wa mstari kwa uharibifu wa utaratibu wa sifuri, tunaweza kuamua kiwango cha mara kwa mara:

$$\ce{slope}=−k=\mathrm{1.3110^{−6}\:mol/L/s} \nonumber$$

Kielelezo$\PageIndex{3}$: Uharibifu wa NH ₃ kwenye uso wa tungsten (W) ni mmenyuko wa sifuri, wakati kwenye uso wa quartz (SiO ₂), majibu ni ya kwanza.

 

Nusu ya maisha ya mmenyuko

Maisha ya nusu ya mmenyuko (t _1/2) ni wakati unaotakiwa kwa nusu moja ya kiasi kilichopewa cha reactant kutumiwa. Katika kila nusu ya maisha ya mafanikio, nusu ya mkusanyiko uliobaki wa reactant hutumiwa. Kutumia kuharibika kwa peroxide ya hidrojeni kama mfano, tunaona kwamba wakati wa nusu ya maisha ya kwanza (kutoka saa 0.00 hadi saa 6.00), mkusanyiko wa H _{2 O 2} hupungua kutoka 1.000 M hadi 0.500 M. Wakati wa nusu ya pili (kutoka saa 6.00 hadi saa 12.00), inapungua kutoka 0.500 M hadi 0.250 M; wakati wa nusu ya maisha ya tatu, inapungua kutoka 0.250 M hadi 0.125 M. Mkusanyiko wa H ₂ O ₂ hupungua kwa nusu wakati wa kila kipindi cha mfululizo wa masaa 6.00. Uharibifu wa peroxide ya hidrojeni ni mmenyuko wa kwanza, na, kama inavyoonekana, nusu ya maisha ya mmenyuko wa kwanza ni huru na mkusanyiko wa mmenyuko. Hata hivyo, nusu ya maisha ya athari na amri nyingine hutegemea viwango vya reactants.

Athari ya Kwanza

Tunaweza kupata equation kwa kuamua nusu ya maisha ya mmenyuko wa kwanza kutoka kwa fomu mbadala ya sheria ya kiwango cha jumuishi kama ifuatavyo:

\ [kuanza {align*}
\ ln\ dfrac {[A] _0} {[A]} &=kt\\ [4pt]
t&=\ ln\ dfrac {[A] _0} {[A]} ×\ dfrac {1} {k}
\ mwisho {align*}\ nonumber\]

Kama sisi kuweka muda t sawa na nusu ya maisha$t_{1/2}$, mkusanyiko sambamba ya A kwa wakati huu ni sawa na nusu ya mkusanyiko wake wa awali. Hivyo, wakati$t=t_{1/2}$,$[A]=\dfrac{1}{2}[A]_0$.

Kwa hiyo:

\ [kuanza {align*}
t_ {1/2} &=\ ln\ dfrac {[A] _0} {\ dfrac {1} {2} [A] _0} ×\ dfrac {1} {k}\\ [4pt]
&=\ ln 2×\ dfrac {1} {k} {1} {k}
mwisho {align*}\ nonumber\]

Hivyo:

$$t_{1/2}=\dfrac{0.693}{k} \nonumber$$

Tunaweza kuona kwamba nusu ya maisha ya mmenyuko wa kwanza ni inversely sawia na kiwango cha mara kwa mara k. Tabia ya haraka (nusu ya maisha mafupi) yatakuwa na k kubwa; mmenyuko wa polepole (muda mrefu wa nusu ya maisha) utakuwa na k ndogo.

Mfano$\PageIndex{5}$: Calculation of a First-order Rate Constant using Half-Life

Tumia kiwango cha mara kwa mara kwa utengano wa kwanza wa peroxide ya hidrojeni katika maji saa 40° C, kwa kutumia data iliyotolewa katika Kielelezo$\PageIndex{4}$.

Kielelezo$\PageIndex{4}$: Uharibifu wa H ₂ O _{2$\ce{(2H2O2⟶2H2O + O2)}$} saa 40 °C unaonyeshwa. Upeo wa rangi unaashiria mkusanyiko wa H ₂ O ₂ katika nyakati zilizoonyeshwa; H ₂ O ₂ ni kweli isiyo rangi.

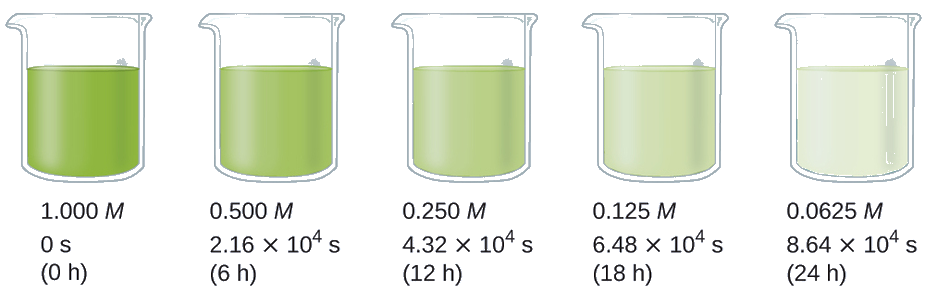
Suluhisho Nusu ya maisha ya kuharibika kwa H _{2 O 2} ni 2.16 × 10 ⁴ s:

\ [kuanza {align*}
t_ {1/2} &=\ dfrac {0.693} {k}\\ [4pt]
k&=\ dfrac {0.693} {t_ {1/2}} =\ dfrac {0.693} {2.16×10^4\:\ ce s} =3.21×10^ {˚ 5}\:\ ce s^ {-1}
\ mwisho {align*}\ nonumber\]

Zoezi$\PageIndex{1}$

Kuoza kwa mionzi ya kwanza ya iodini-131 inaonyesha kiwango cha mara kwa mara cha ^{0.138 d -1}. Nusu ya maisha ya kuoza hii ni nini?

Jibu

5.02 d.

 

Pili ili Athari

Tunaweza kupata equation kwa kuhesabu nusu ya maisha ya utaratibu wa pili kama ifuatavyo:

$$\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \nonumber$$

au

$$\dfrac{1}{[A]}−\dfrac{1}{[A]_0}=kt \nonumber$$

Kama

$$t=t_{1/2} \nonumber$$

basi

$$[A]=\dfrac{1}{2}[A]_0 \nonumber$$

na tunaweza kuandika:

\ (kuanza {align*}
\ dfrac {1} {\ dfrac {1} {2} [A] _0}}}\ dfrac {1} {[A] _0} &=kt_ {1/2}\ [4pt]
2 [A] _0\\ [4pt] 2 [A] _0} {[A] _0} &=kt_ {1/2}\\ [4pt] pt]
\ dfrac {1} {[A] _0} &=kt_ {1/2}
\ mwisho {align*}\)

Hivyo:

$$t_{1/2}=\dfrac{1}{k[A]_0} \nonumber$$

Kwa majibu ya pili ili,$t_{1/2}$ ni inversely sawia na mkusanyiko wa reactant, na nusu ya maisha kuongezeka kama majibu yanaendelea kwa sababu mkusanyiko wa reactant itapungua. Kwa hiyo, tunaona matumizi ya dhana ya nusu ya maisha kuwa ngumu zaidi kwa athari za pili kuliko kwa athari za kwanza. Tofauti na athari za utaratibu wa kwanza, mara kwa mara ya kiwango cha mmenyuko wa pili hawezi kuhesabiwa moja kwa moja kutoka nusu ya maisha isipokuwa ukolezi wa awali unajulikana.

 

Zero Order Athari

Tunaweza kupata equation kwa kuhesabu nusu ya maisha ya mmenyuko wa utaratibu wa sifuri kama ifuatavyo:

$$[A]=−kt+[A]_0 \nonumber$$

Wakati nusu ya kiasi ya awali ya reactant imekuwa zinazotumiwa$t=t_{1/2}$ na$[A]=\dfrac{[A]_0}{2}$. Hivyo:

\ [kuanza {align*}
\ dfrac {[A] _0} {2} &=-kt_ {1/2} + [A] _0\ [4pt]
kt_ {1/2} &=\ dfrac {[A] _0} {2}
\ mwisho {align*}\ nonumber\]

na

$$t_{1/2}=\dfrac{[A]_0}{2k} \nonumber$$

Maisha ya nusu ya mmenyuko wa sifuri huongezeka kama ukolezi wa awali unavyoongezeka. Ulinganisho wa sheria za kiwango cha tofauti na jumuishi na nusu ya maisha ya sambamba kwa athari za sifuri, za kwanza, na za pili zinafupishwa katika Jedwali$\PageIndex{1}$.

Jedwali$\PageIndex{1}$: Muhtasari wa Sheria za Kiwango cha Zero-, Kwanza, na Pili-Order Reactions

	Zero-Order	Amri ya Kwanza	Pili-Order
kiwango cha sheria	kiwango = k	kiwango = k [A]	kiwango = k [A] ^2
vitengo vya kiwango cha mara kwa mara	M ^s -1	^s -1	M ^-1 ^s -1
jumuishi kiwango cha sheria	[A] = - kt + [A] 0	ln [A] = - kt + ln [A] 0	$\dfrac{1}{[A]}=kt+\left(\dfrac{1}{[A]_0}\right)$
njama zinahitajika kwa ajili ya fit linear ya kiwango cha data	[A] vs t	ln [A] vs t	$\dfrac{1}{[A]}$dhidi ya t
uhusiano kati ya mteremko wa njama linear na kiwango cha mara kwa mara	k = -mteremko	k = -mteremko	k = +mteremko
nusu ya maisha	$t_{1/2}=\dfrac{[A]_0}{2k}$	$t_{1/2}=\dfrac{0.693}{k}$	$t_{1/2}=\dfrac{1}{[A]_0k}$

 

Muhtasari

Sheria za kiwango cha tofauti zinaweza kuamua kwa njia ya viwango vya awali au njia nyingine. Tunapima maadili kwa viwango vya awali vya mmenyuko katika viwango tofauti vya reactants. Kutoka kwa vipimo hivi, tunaamua utaratibu wa mmenyuko katika kila reactant. Sheria za kiwango cha jumuishi zinatambuliwa na ushirikiano wa sheria za kiwango cha tofauti. Kiwango cha mara kwa mara kwa sheria hizo za kiwango kinatambuliwa kutoka kwa vipimo vya ukolezi kwa nyakati mbalimbali wakati wa majibu.

Nusumaisha ya mmenyuko ni wakati unaotakiwa kupunguza kiasi cha reactant iliyotolewa kwa nusu moja. Maisha ya nusu ya mmenyuko wa sifuri hupungua kama ukolezi wa awali wa mmenyuko katika mmenyuko unapungua. Maisha ya nusu ya mmenyuko wa kwanza ni huru ya ukolezi, na nusu ya maisha ya mmenyuko wa pili hupungua kadiri ukolezi unavyoongezeka.

Mlinganyo muhimu

• sheria ya kiwango cha jumuishi kwa athari za utaratibu wa sifuri (Equation\ ref {intzero}):

$[A]=−kt+[A]_0$na$t_{1/2}=\dfrac{[A]_0}{2k}$

• jumuishi kiwango cha sheria kwa ajili ya athari ya kwanza ili (Equation\ ref {in1st}):

$\ln[A]=−kt+ \ln[A]_0$na$t_{1/2}=\dfrac{0.693}{k}$

• jumuishi kiwango cha sheria kwa ajili ya athari ya pili ili (Equation\ ref {int2nd}):

$\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0}$na$t_{1/2}=\dfrac{1}{[A]_0k}$

faharasa

nusu ya maisha ya mmenyuko (t _l/2)

muda required kwa ajili ya nusu ya kiasi fulani ya reactant kuwa zinazotumiwa

jumuishi kiwango cha sheria

equation kwamba inahusiana mkusanyiko wa reactant kwa muda ilipita ya mmenyuko