16.3: Hisabati ya Mawimbi

Malengo ya kujifunza

• Mfano wimbi, kusonga kwa kasi ya wimbi la mara kwa mara, na kujieleza hisabati
• Tumia kasi na kasi ya kati
• Onyesha jinsi kasi ya kati inatofautiana na kasi ya wimbi (kasi ya uenezi)

Katika sehemu iliyopita, tulielezea mawimbi ya mara kwa mara kwa sifa zao za wavelength, kipindi, amplitude, na kasi ya wimbi la wimbi. Mawimbi yanaweza pia kuelezewa na mwendo wa chembe za kati ambayo mawimbi huhamia. Msimamo wa chembe za kati zinaweza kuhesabiwa hesabu kama kazi ya wimbi s, ambayo inaweza kutumika kupata nafasi, kasi, na kuongeza kasi ya chembe za kati ya wimbi wakati wowote.

Pulses

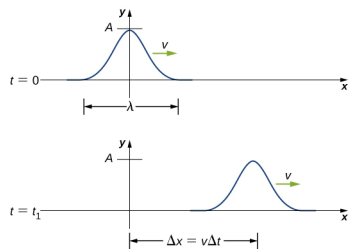
Pigo inaweza kuelezewa kama wimbi linalojumuisha usumbufu mmoja unaoendelea kupitia kati na amplitude ya mara kwa mara. Pigo huenda kama mfano unaoendelea sura yake kama inavyoeneza kwa kasi ya wimbi la mara kwa mara. Kwa sababu kasi ya wimbi ni mara kwa mara, umbali wa pigo huenda kwa wakati Δt ni sawa na Δx = vΔt (Kielelezo\(\PageIndex{1}\)).

Kielelezo\(\PageIndex{1}\): Pigo wakati t = 0 inazingatia x = 0 na amplitude A. Pigo huenda kama mfano na sura ya mara kwa mara, na thamani ya juu ya mara kwa mara A. Kasi ni mara kwa mara na pigo huenda umbali Δx = vΔt kwa wakati Δt. Umbali uliosafiri unapimwa kwa hatua yoyote rahisi juu ya pigo. Katika takwimu hii, kiumbe kinatumiwa.

Mfano wa Wimbi la Sinusoidal Moja kwa moja Kutumia Kazi ya Wave

Fikiria kamba iliyohifadhiwa kwa mvutano wa mara kwa mara\(F_T\) ambapo mwisho mmoja umewekwa na mwisho wa bure unafungwa kati\(y = +A\) na\(y = −A\) kwa kifaa cha mitambo kwa mzunguko wa mara kwa mara. Kielelezo\(\PageIndex{2}\) kinaonyesha picha za wimbi wakati wa kipindi cha nane ya kipindi, kuanzia baada ya kipindi kimoja (\(t = T\)).

Kielelezo\(\PageIndex{2}\): Snapshots ya wimbi transverse kusonga kupitia kamba chini ya mvutano, kuanzia wakati\(t = T\) na kuchukuliwa kwa vipindi vya\(\frac{1}{8}T\). Dots za rangi hutumiwa kuonyesha pointi kwenye kamba. Pointi ambazo ni wavelength mbali katika x -mwelekeo ni yalionyesha na dots sawa rangi.

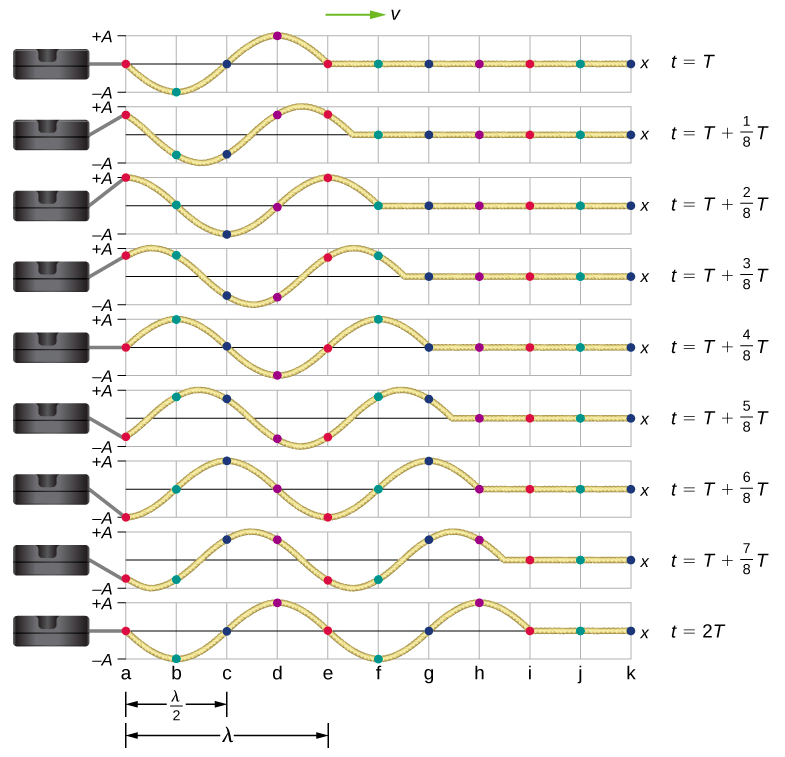
Kumbuka kwamba kila hatua ya kuchagua juu ya kamba (alama na dots rangi) oscillates juu na chini katika rahisi harmonic mwendo\(y = −A\), kati\(y = +A\) na, kwa kipindi\(T\). Wimbi kwenye kamba ni sinusoidal na linatafsiri katika mwelekeo mzuri wa x-kama wakati unavyoendelea.

Kwa hatua hii, ni muhimu kukumbuka kutokana na utafiti wako wa algebra kwamba ikiwa\(f(x)\) ni kazi fulani, basi\(f(x−d)\) ni kazi sawa iliyotafsiriwa katika mwelekeo mzuri wa x-kwa umbali\(d\). Kazi\(f(x+d)\) ni kazi sawa iliyotafsiriwa katika mwelekeo mbaya wa x-kwa umbali\(d\). Tunataka kufafanua kazi wimbi kwamba nitakupa\(y\) -nafasi ya kila sehemu ya kamba kwa kila x msimamo pamoja kamba kwa kila wakati\(t\).

Kuangalia snapshot ya kwanza kwenye Kielelezo\(\PageIndex{2}\), msimamo wa y wa kamba kati\(x = 0\) na\(x = λ\) unaweza kuonyeshwa kama kazi ya sine. Wimbi hili hueneza chini ya kamba moja wavelength katika kipindi kimoja, kama inavyoonekana katika snapshot ya mwisho. wimbi kwa hiyo hatua na kasi ya mara kwa mara wimbi la\(v = λ/T\).

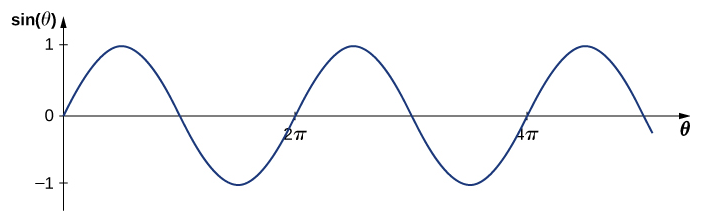
Kumbuka kwamba kazi ya sine ni kazi ya angle\(θ\), ikisonga kati ya +1 na -1, na kurudia kila\(2π\) radians (Kielelezo\(\PageIndex{3}\)). Hata hivyo, y -nafasi ya kati, au kazi ya wimbi, oscillates kati\(+A\) na\(−A\), na kurudia kila wavelength\(λ\).

Kielelezo\(\PageIndex{3}\): kazi sine oscillates kati +1 na -1 kila 2π radians.

Ili kujenga mfano wetu wa wimbi kwa kutumia kazi ya mara kwa mara, fikiria uwiano wa angle na nafasi,

\[\begin{align*} \dfrac{\theta}{x} &=\frac{2 \pi}{\lambda}, \\[4pt] \theta &=\frac{2 \pi}{\lambda} x. \end{align*}\]

Kutumia\(\theta = \frac{2\pi}{\lambda}x\) na kuzidisha kazi ya sine kwa amplitude A, sasa tunaweza kuiga y -nafasi ya kamba kama kazi ya msimamo x:

\[ y(x)=A \sin \left(\frac{2 \pi}{\lambda} x\right). \nonumber \]

wimbi kwenye kamba husafiri katika chanya x -mwelekeo na kasi ya mara kwa mara v, na hatua umbali vt katika wakati t. Kazi ya wimbi sasa inaweza kuelezwa na

\[ y(x, t)=A \sin \left(\frac{2 \pi}{\lambda}(x-v t)\right). \nonumber \]

Mara nyingi ni rahisi kuandika upya kazi hii ya wimbi kwa fomu zaidi. Kuongezeka kwa njia ya uwiano\(\frac{2\pi}{\lambda}\) husababisha equation

\[ y(x, t)=A \sin \left(\frac{2 \pi}{\lambda} x-\frac{2 \pi}{\lambda} v t\right). \nonumber \]

Thamani\(\frac{2\pi}{\lambda}\) hufafanuliwa kama nambari ya wimbi. Ishara ya nambari ya wimbi ni k na ina vitengo vya mita za inverse^{, m -1}:

\[ k \equiv \frac{2 \pi}{\lambda} \label{16.2} \]

Kumbuka kutoka kwa Oscillations kwamba mzunguko wa angular hufafanuliwa kama\(\omega \equiv \frac{2\pi}{T}\). Muda wa pili wa kazi ya wimbi inakuwa

\[\frac{2 \pi}{\lambda} v t=\frac{2 \pi}{\lambda}\left(\frac{\lambda}{T}\right) t=\frac{2 \pi}{T} t=\omega t. \nonumber \]

Kazi ya wimbi kwa wimbi rahisi la harmonic kwenye kamba hupunguza

\[ y(x, t)=A \sin (k x \mp \omega t) \nonumber \]

ambapo A ni amplitude,\(k = \frac{2\pi}{\lambda}\) ni namba ya wimbi,\(\omega = \frac{2\pi}{T}\) ni mzunguko wa angular, ishara ndogo ni kwa mawimbi yanayohamia katika mwelekeo mzuri wa x, na ishara ya pamoja ni kwa mawimbi yanayohamia kwenye mwelekeo mbaya wa x. Kasi ya wimbi ni sawa na

\[ v=\frac{\lambda}{T}=\frac{\lambda}{T}\left(\frac{2 \pi}{2 \pi}\right)=\frac{\omega}{k} \label{16.3} .\]

Fikiria nyuma kwenye majadiliano yetu ya wingi juu ya chemchemi, wakati nafasi ya molekuli ilikuwa inatokana kama

\[x(t) = A \cos(ωt+ϕ). \nonumber\]

Pembe\(ϕ\) ni mabadiliko ya awamu, imeongezwa ili kuruhusu ukweli kwamba wingi unaweza kuwa na hali ya awali isipokuwa\(x = +A\) na\(v = 0\). Kwa sababu sawa, awamu ya awali imeongezwa kwenye kazi ya wimbi. Kazi ya wimbi mfano wa wimbi la sinusoidal, kuruhusu mabadiliko ya awamu ya awali\(ϕ\), ni

\[ y(x, t)=A \sin (k x \mp \omega t+\phi) \label{16.4} \]

Thamani

\[ (k x \mp \omega t+\phi) \label{16.5} \]

inajulikana kama awamu ya wimbi, ambapo\(\phi\) ni awamu ya awali ya kazi ya wimbi. Ikiwa neno la muda\(\omega t\) ni hasi au chanya linategemea mwelekeo wa wimbi. Kwanza fikiria ishara ndogo kwa wimbi na awamu ya awali sawa na sifuri (\(\phi\)= 0). Awamu ya wimbi itakuwa (\(kx = \omega t\)). Fikiria kufuata hatua juu ya wimbi, kama vile crest. Muungano utatokea wakati\(\sin(kx - \omega t = 1.00\), yaani, wakati\(k x-\omega t=n \pi+\frac{\pi}{2}\), kwa thamani yoyote muhimu ya n. Kwa mfano, kiumbe kimoja kinachotokea\(k x-\omega t=\frac{\pi}{2}\). Kama wimbi linakwenda, wakati unaongezeka na x lazima pia iongeze ili kuweka awamu sawa na\(\frac{\pi}{2}\). Kwa hiyo, ishara ndogo ni kwa wimbi linalohamia katika mwelekeo mzuri wa x. Kutumia ishara ya pamoja,\(k x+\omega t=\frac{\pi}{2}\). Wakati unapoongezeka, x lazima ipunguze ili kuweka awamu sawa na\(\frac{\pi}{2}\). Ishara ya pamoja hutumiwa kwa mawimbi yanayohamia kwenye mwelekeo mbaya wa x. Kwa muhtasari,\(y(x, t)=A \sin (k x-\omega t+\phi)\) mifano wimbi kusonga katika chanya x -mwelekeo na\(y(x, t)=A \sin (k x+\omega t+\phi)\) mifano wimbi kusonga katika hasi x -direction.

Equation\ ref {16.4} inajulikana kama kazi rahisi ya wimbi la harmonic. Kazi ya wimbi ni kazi yoyote kama hiyo\(f(x, t)=f(x-v t)\). Baadaye katika sura hii, tutaona kwamba ni suluhisho la equation linear wimbi. Kumbuka kwamba\(y(x, t)=A \cos \left(k x+\omega t+\phi^{\prime}\right)\) kazi sawa vizuri kwa sababu inafanana na mabadiliko tofauti ya awamu\(\phi^{\prime}=\phi-\frac{\pi}{2}\).

Kupata sifa za wimbi la sinusoidal

1. Ili kupata amplitude, wavelength, kipindi, na mzunguko wa wimbi la sinusoidal, weka kazi ya wimbi kwa fomu\(y(x, t)=A \sin (k x-\omega t+\phi)\).
2. Amplitude inaweza kusoma moja kwa moja kutoka equation na ni sawa na\(A\).
3. Kipindi cha wimbi kinaweza kupatikana kutoka kwa mzunguko wa angular\( \left(T=\frac{2 \pi}{\omega}\right)\).
4. Mzunguko unaweza kupatikana kwa kutumia\(f = \frac{1}{T}\)
5. Urefu wa wavelength unaweza kupatikana kwa kutumia nambari ya wimbi\(\left(\lambda=\frac{2 \pi}{k}\right)\).

Mfano\(\PageIndex{1}\): Characteristics of a traveling wave on a string

Wimbi la transverse kwenye kamba ya taut linatokana na kazi ya wimbi

\[ \begin{align*} y(x, t) &=A \sin (k x-w t) \\[4pt] &= (0.2 \: \mathrm{m}) \sin \left(6.28 \: \mathrm{m}^{-1} x-1.57 \: \mathrm{s}^{-1} t\right) \end{align*} \]

Pata amplitude, wavelength, kipindi, na kasi ya wimbi.

Mkakati

Tabia hizi zote za wimbi zinaweza kupatikana kutoka kwa vipindi vilivyojumuishwa katika equation au kutoka kwa mchanganyiko rahisi wa vipindi hivi.

Suluhisho

1. Amplitude, nambari ya wimbi, na mzunguko wa angular inaweza kusoma moja kwa moja kutoka kwa usawa wa wimbi:

\ kuanza {align*}
y (x, t) =& A\ kuzama (k x-w t) =0.2\:\ hesabu {m}\ dhambi\ kushoto (6.28\:\ hesabu {m} ^ {-1} x-1.57\:\ hesabu {s} ^ {-1} t\ haki)\ nonumber\\
& kushoto (A=0.2\:\ m {m}; k=6.28\:\ mathrm {m} ^ {-1};\ omega = 1.57\:\ hesabu {s} ^ {-1}\ haki)\ nonnumber
\ mwisho {align*}

2. Nambari ya wimbi inaweza kutumika kupata wavelength:

\ kuanza {safu} {l}
k=\ frac {2\ pi} {\ lambda}\\ lambda}
\\ lambda =\ frac {2\ pi} {k} =\ frac {2\ pi} {6.28\:\ mathrm {m} ^ {-1}} =1.0\:\ mathrm {m}
\ mwisho {safu}

3. Kipindi cha wimbi kinaweza kupatikana kwa kutumia mzunguko wa angular:

\ kuanza {safu} {l}
\ omega =\ frac {2\ pi} {T}\\
T=\ Frac {2\ pi} {\ omega} =\ frac {2\ pi} {1.57\:\ mathrm {s} ^ {-1}} =4\:\ mathrm {s}
\ mwisho {safu}

4. Kasi ya wimbi inaweza kupatikana kwa kutumia nambari ya wimbi na mzunguko wa angular. Mwelekeo wa wimbi unaweza kuamua kwa kuzingatia ishara ya\(k x \mp \omega t\): Ishara hasi inaonyesha kwamba wimbi linasonga katika mwelekeo mzuri wa x:

\[ |v|=\frac{\omega}{k}=\frac{1.57 \: \mathrm{s}^{-1}}{6.28 \: \mathrm{m}^{-1}}=0.25 \: \mathrm{m} / \mathrm{s} \nonumber\]

Umuhimu

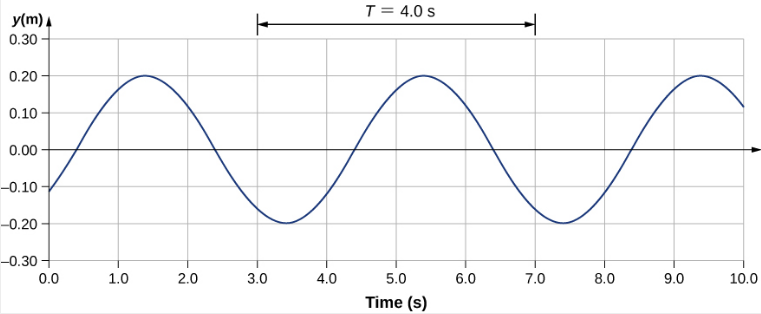
Tabia zote za wimbi zinazomo katika kazi ya wimbi. Kumbuka kuwa kasi ya wimbi ni kasi ya wimbi katika mwelekeo sambamba na mwendo wa wimbi. Kupanga urefu wa y kati dhidi ya msimamo x kwa mara mbili t = 0.00 s na t = 0.80 s inaweza kutoa taswira ya graphical ya wimbi (Kielelezo\(\PageIndex{4}\)).

Kielelezo\(\PageIndex{4}\): Grafu ya urefu wa wimbi y kama kazi ya msimamo x kwa picha za wimbi mara mbili. Mstari wa dotted unawakilisha wimbi kwa wakati t = 0.00 s na mstari imara inawakilisha wimbi saa t = 0.80 s.Kwa kuwa kasi ya wimbi ni mara kwa mara, umbali wa wimbi husafiri ni kasi ya wimbi mara wakati. Dots nyeusi zinaonyesha pointi zilizotumiwa kupima uhamisho wa wimbi. Ya kati huenda juu na chini, wakati wimbi linakwenda kulia.

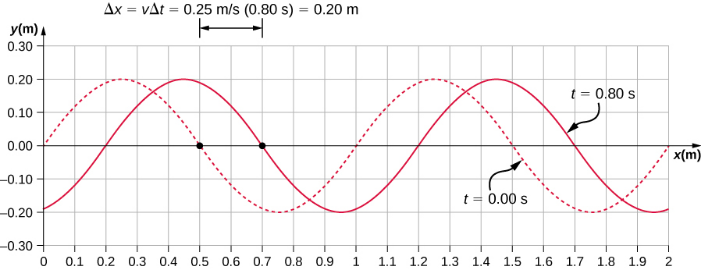
Kuna kasi ya pili kwa mwendo. Katika mfano huu, wimbi ni transverse, kusonga kwa usawa kama kati oscillates juu na chini perpendicular kwa mwelekeo wa mwendo. Grafu katika Kielelezo\(\PageIndex{5}\) inaonyesha mwendo wa kati katika hatua x = 0.60 m kama kazi ya wakati. Ona kwamba kati ya wimbi oscillates juu na chini kati ya y = +0.20 m na y = -0.20 m kila kipindi cha sekunde 4.0.

Kielelezo\(\PageIndex{5}\): Grafu ya urefu wa wimbi y kama kazi ya muda t kwa nafasi x = 0.6 m. kati oscillates kati ya y = +0.20 m na y = -0.20 m kila kipindi. Kipindi kilichowakilishwa tar pointi mbili rahisi katika oscillations kupima kipindi. Kipindi kinaweza kupimwa kati ya pointi mbili zilizo karibu na amplitude sawa na kasi sawa,\((\partial y / \partial t)\). Kasi inaweza kupatikana kwa kuangalia tangent ya mteremko hadi hatua kwenye njama ya y -versus- t. Kumbuka kwamba wakati mwingine t = 3.00 s na t = 7.00 s, urefu na kasi ni sawa na kipindi cha oscillation ni 4.00 s.

Zoezi\(\PageIndex{1}\)

Kazi ya wimbi hapo juu inatokana na kazi ya sine. Je, kazi ya cosine inaweza kutumika badala yake?

Velocity na kuongeza kasi ya Kati

Kama inavyoonekana katika Mfano\(\PageIndex{2}\), kasi ya wimbi ni mara kwa mara na inawakilisha kasi ya wimbi jinsi inavyoenea kwa njia ya kati, si kasi ya chembe zinazounda kati. Vipande vya kati huzunguka karibu na msimamo wa usawa kama wimbi linaenea kwa njia ya kati. Katika kesi ya wimbi la transverse linaloenea katika mwelekeo wa x, chembe hupanda juu na chini katika mwelekeo wa y, perpendicular kwa mwendo wa wimbi. Kasi ya chembe za kati sio mara kwa mara, ambayo inamaanisha kuna kasi. Kasi ya kati, ambayo ni perpendicular kwa kasi ya wimbi katika wimbi transverse, inaweza kupatikana kwa kuchukua derivative sehemu ya msimamo equation kwa heshima na wakati. Derivative ya sehemu inapatikana kwa kuchukua derivative ya kazi, kutibu vigezo vyote kama mara kwa mara, ila kwa kutofautiana katika swali. Katika kesi ya derivative sehemu kwa heshima na muda\(t\), nafasi\(x\) ni kutibiwa kama mara kwa mara. Ingawa hii inaweza sauti ya ajabu kama hujaona kabla, kitu cha zoezi hili ni kupata kasi transverse katika hatua, hivyo kwa maana hii,\(x\) msimamo - si kubadilisha. Tuna

\[\begin{split} y(x,t) & = A \sin (kx - \omega t + \phi) \\ v_{y} (x,t) & = \frac{\partial y(x,t)}{\partial t} = \frac{\partial}{\partial t} [A \sin (kx - \omega t + \phi)] \\ & = -A \omega \cos (kx - \omega t + \phi) \\ & = -v_{y\; max} \cos (kx - \omega t + \phi) \ldotp \end{split}\]

Ukubwa wa kasi ya juu ya kati ni\(|v_{y\, max}| = A \omega\). Hii inaweza kuangalia ukoo kutoka Oscillations na wingi juu ya spring.

Tunaweza kupata kasi ya kati kwa kuchukua derivative sehemu ya equation kasi kwa heshima na wakati,

\[\begin{split} a_{y} (x,t) & = \frac{\partial v_{y}(x,t)}{\partial t} = \frac{\partial}{\partial t} [-A \omega \cos (kx - \omega t + \phi)] \\ & = -A \omega^{2} \sin (kx - \omega t + \phi) \\ & = -a_{y\; max} \sin (kx - \omega t + \phi) \ldotp \end{split}\]

Ukubwa wa kasi ya kiwango cha juu ni |a _{y max} | = A\(\omega^{2}\). Vipande vya kati, au vipengele vya wingi, hutembea kwa mwendo rahisi wa harmonic kwa wimbi la mitambo.

Ulinganisho wa Wimbi la mstari

Tumeamua tu kasi ya kati katika msimamo x kwa kuchukua sehemu ya derivative, kwa heshima ya wakati, ya nafasi y Kwa wimbi la mzunguko, kasi hii ni perpendicular kwa mwelekeo wa uenezi wa wimbi. Tulipata kuongeza kasi kwa kuchukua derivative sehemu, kwa heshima na wakati, ya kasi, ambayo ni mara ya pili derivative ya nafasi:

\[a_{y} (x,t) = \frac{\partial^{2} y(x,t)}{\partial t^{2}} = \frac{\partial^{2}}{\partial t^{2}} [A \sin(kx - \omega t + \phi)] = -A \omega^{2} \sin (kx - \omega t + \phi) \ldotp\]

Sasa fikiria derivatives ya sehemu kwa heshima na variable nyingine, nafasi x, kufanya mara kwa mara wakati. Derivative ya kwanza ni mteremko wa wimbi kwa uhakika x wakati t,

\[slope = \frac{\partial y(x,t)}{\partial x} = \frac{\partial}{\partial x} [A \sin (kx - \omega t + \phi)] = Ak \cos (kx - \omega t + \phi) \ldotp\]

Derivative ya pili ya sehemu inaonyesha jinsi mteremko wa wimbi hubadilika kwa heshima na msimamo-kwa maneno mengine, ukingo wa wimbi, wapi

\[curvature = \frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{\partial^{2}}{\partial x^{2}} [A \sin (kx - \omega t + \phi)] = -Ak^{2} \sin (kx - \omega t + \phi) \ldotp\]

Uwiano wa kuongeza kasi na ukingo unasababisha uhusiano muhimu sana katika fizikia unaojulikana kama equation ya wimbi linear. Kuchukua uwiano na kutumia equation v =\(\frac{\omega}{k}\) hutoa equation ya wimbi la mstari (pia inajulikana tu kama equation ya wimbi au equation ya kamba ya vibrating),

\[\begin{split} \frac{\frac{\partial^{2} y(x,t)}{\partial t^{2}}}{\frac{\partial^{2} y(x,t)}{\partial x^{2}}} & = \frac{-A \omega^{2} \sin (kx - \omega t + \phi)}{-Ak^{2} \sin (kx - \omega t + \phi)} \\ & = \frac{\omega^{2}}{k^{2}} = v^{2}, \end{split}\]

\[\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}} \ldotp \label{16.6}\]

Equation\ ref {16.6} ni equation linear wimbi, ambayo ni moja ya milinganyo muhimu katika fizikia na uhandisi. Tuliipata hapa kwa wimbi la mzunguko, lakini ni muhimu pia wakati wa kuchunguza mawimbi ya longitudinal. Uhusiano huu ulitokana pia kwa kutumia wimbi la sinusoidal, lakini linaelezea kwa ufanisi wimbi lolote au pigo lolote ambalo lina fomu y (x, t) = f (x vt). Mawimbi haya matokeo kutokana na linear kurejesha nguvu ya kati-hivyo, jina linear wimbi equation. Kazi yoyote ya wimbi ambayo inatimiza equation hii ni kazi ya wimbi la mstari.

Kipengele cha kuvutia cha equation ya wimbi linear ni kwamba ikiwa kazi mbili za wimbi ni ufumbuzi mmoja mmoja kwa equation ya wimbi la mstari, basi jumla ya kazi mbili za wimbi linear pia ni suluhisho la equation ya wimbi. Fikiria mawimbi mawili yanayozunguka ambayo hueneza kando ya x-axis, ikichukua katikati sawa. Fikiria kwamba mawimbi ya mtu binafsi yanaweza kuonyeshwa na kazi za wimbi y ₁ (x, t) = f (x vt) na y ₂ (x, t) = g (x vt), ambayo ni ufumbuzi wa equations ya wimbi linear na kwa hiyo ni kazi ya wimbi linear. Jumla ya kazi za wimbi ni kazi ya wimbi

\[y_{1} (x,t) + y_{2} (x,t) = f(x \mp vt) + g(x \mp vt) \ldotp\]

Fikiria usawa wa wimbi la mstari:

\[\begin{split} \frac{\partial^{2} (f + g)}{\partial x^{2}} & = \frac{1}{v^{2}} \frac{\partial^{2} (f + g)}{\partial t^{2}} \\ \frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial^{2} g}{\partial x^{2}} & = \frac{1}{v^{2}} \left(\dfrac{\partial^{2} f}{\partial t^{2}} + \frac{\partial^{2} g}{\partial t^{2}}\right) \ldotp \end{split}\]

Hii imeonyesha kwamba ikiwa kazi mbili za wimbi linear zinaongezwa algebraically, kazi ya wimbi inayosababisha pia ni ya mstari. Kazi hii ya wimbi inafanana na uhamisho wa kati ya wimbi linalosababisha kila nafasi pamoja na x-axis. Ikiwa mawimbi mawili ya mstari huchukua katikati sawa, wanasemekana kuingilia kati. Ikiwa mawimbi haya yanaweza kuonyeshwa na kazi ya wimbi linear, kazi hizi za wimbi huongeza kuunda equation ya wimbi la wimbi kutokana na kuingiliwa kwa mawimbi ya mtu binafsi. Uhamisho wa kati katika kila hatua ya wimbi linalosababisha ni jumla ya algebraic ya uhamisho kutokana na mawimbi ya mtu binafsi.

Kuchukua uchambuzi huu hatua zaidi, ikiwa kazi ya wimbi y1 (x, t) = f (x vt) na y2 (x, t) = g (x vt) ni ufumbuzi wa equation ya wimbi la mstari, basi Ay ₁ (x, t) + By ₂ (x, y), ambapo A na B ni mara kwa mara, pia ni suluhisho la equation ya wimbi la mstari. Mali hii inajulikana kama kanuni ya superposition. Kuingilia kati na superposition ni kufunikwa kwa undani zaidi katika Kuingiliwa kwa Waves

Mfano\(\PageIndex{2}\): Interference of Waves on a String

Fikiria kamba ndefu sana uliofanyika taut na wanafunzi wawili, moja juu ya kila mwisho. Mwanafunzi A oscillates mwisho wa kamba kuzalisha wimbi inatokana na wimbi kazi y ₁ (x, t) = dhambi (kx -\(\omega\) t) na mwanafunzi B oscillates kamba kuzalisha mara mbili frequency, kusonga katika mwelekeo kinyume. Wote mawimbi hoja kwa kasi sawa v =\(\frac{\omega}{k}\). Mawimbi mawili yanaingilia kati ili kuunda wimbi linalosababisha ambalo kazi ya wimbi ni y _R (x, t) = y ₁ (x, t) + y ₂ (x, t). Kupata kasi ya wimbi kusababisha kutumia linear wimbi equation\(\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}}\).

Mkakati

Kwanza, weka kazi ya wimbi kwa wimbi lililoundwa na mwanafunzi wa pili. Kumbuka kuwa mzunguko wa angular wa wimbi la pili ni mara mbili mzunguko wa wimbi la kwanza (2\(\omega\)), na kwa kuwa kasi ya mawimbi mawili ni sawa, idadi ya wimbi la pili ni mara mbili ya wimbi la kwanza (2k). Kisha, weka equation ya wimbi kwa kazi ya wimbi inayosababisha, ambayo ni jumla ya kazi mbili za wimbi la mtu binafsi. Kisha kupata derivative ya pili ya sehemu kwa heshima na msimamo na derivative ya pili ya sehemu kwa heshima na wakati. Tumia equation ya wimbi la mstari ili kupata kasi ya wimbi linalosababisha.

Suluhisho

1. Andika kazi ya wimbi la wimbi la pili: y ₂ (x, t) = dhambi (2kx + 2\(\omega\) t).
2. Andika kazi ya wimbi inayosababisha: $$y_ {R} (x, t) = y_ {1} (x, t) + y (x, t) = A\ dhambi (kx -\ omega t) + A\ dhambi (2kx + 2\ omega t)\ ldotp$$
3. Kupata derivatives sehemu: $$\ kuanza {mgawanyiko}\ Frac {\ sehemu y_ {R} (x, t)} {\ sehemu x} & = -Ak\ cos (kx -\ omega t) + 2Ak\ cos (2kx + 2\ omega t),\\\ frac {\ sehemu ^ {2} y_ {R} (x, t)} {\ sehemu x ^ {2}} & = -Ak^ {2}\ dhambi (kx -\ omega t) - 4Ak ^ {2}\ dhambi (2kx + 2\ omega t),\\\ frac {\ sehemu y_ {R} (x, t)} {\ sehemu t} & = -A\ omega\ cos (kx -\ omega t) + 2A\ omega\ cos (2kx + 2\ omega t),\\ FRAC {\ sehemu ^ {2} y_ {R} (x, t)} {\ sehemu t^ {2}} & = -A\ omega^ {2}\ dhambi (KX -\ omega t) - 4A\ omega ^ {2}\ dhambi (2kx + 2\ omega t)\ ldotp\ mwisho {mgawanyiko} $$
4. Tumia equation ya wimbi ili kupata kasi ya wimbi linalosababisha: $$\ kuanza {split}\ frac {\ partial^ {2} y (x, t)} {\ sehemu x ^ {2}} & =\ frac {1} {v^ {2}}\ frac {\ partial^ {2}}\ -ak^ {2}\ dhambi (kx -\ omega t) + 4Ak^ {2}\ dhambi (2kx + 2\ omega t) & =\ frac {1} {v^ {2}}\ kushoto (-A\ omega ^ {2}\ dhambi (kx -\ omega t) - 4A\ omega ^ {2}\ dhambi (2kx + 2\ omega t)\ haki),\\ k^ {2}\ kushoto (-A\ dhambi (KX -\ omega t) + 4A\ dhambi (2kx + 2\ omega t)\ haki) & =\ frac {\ omega ^ {2}} {v^ {2}}\ kushoto (-A\ dhambi (KX -\ omega t) - 4A\ dhambi (2kx + 2\ omega t)\ haki),\\ k^ {2} & =\ frac {\ omega ^ {2}} {v^ {2}},\\ |v| & =\ frac {\ omega} {k}\ ldotp\ mwisho {split} $$

Umuhimu

Kasi ya wimbi linalosababisha ni sawa na kasi ya mawimbi ya awali\(\left(v = \frac{\omega}{k}\right)\). Tutaonyesha katika sehemu inayofuata kwamba kasi ya wimbi rahisi la harmonic kwenye kamba inategemea mvutano katika kamba na wingi kwa urefu wa kamba. Kwa sababu hii, haishangazi kwamba mawimbi ya sehemu pamoja na wimbi la matokeo yote husafiri kwa kasi sawa.

Zoezi 16.4

Equation ya wimbi\(\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}}\) inafanya kazi kwa wimbi lolote la fomu y (x, t) = f (x vt). Katika sehemu iliyopita, tulisema kuwa kazi ya cosine inaweza pia kutumika kutengeneza wimbi rahisi la mitambo ya harmonic. Angalia kama wimbi

\[y(x,t) = (0.50\; m) \cos (0.20 \pi\; m^{-1} x - 4.00 \pi s^{-1} t + \frac{\pi}{10})\]

ni suluhisho la equation ya wimbi.

Usumbufu wowote unaokubaliana na equation ya wimbi unaweza kueneza kama wimbi linalohamia kando ya mhimili wa x na kasi ya wimbi v. Inafanya kazi sawa kwa mawimbi kwenye kamba, mawimbi ya sauti, na mawimbi ya umeme. Equation hii ni muhimu sana. Kwa mfano, inaweza kutumika kuonyesha kwamba mawimbi ya sumakuumeme huhamia kwa kasi ya nuru.