Skip to main content
Global

15.5: Pendulums

  1. Last updated
  2. Save as PDF
  • Page ID
    177007

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Hali majeshi ambayo hufanya juu ya pendulum rahisi
    • Kuamua mzunguko wa angular, mzunguko, na kipindi cha pendulum rahisi kulingana na urefu wa pendulum na kuongeza kasi kutokana na mvuto
    • Eleza kipindi cha pendulum ya kimwili
    • Eleza kipindi cha pendulum ya torsional

    Pendulums ni katika matumizi ya kawaida. Saa za babu hutumia pendulum kushika muda na pendulum inaweza kutumika kupima kasi kutokana na mvuto. Kwa uhamisho mdogo, pendulum ni oscillator rahisi ya harmonic.

    Pendulum rahisi

    Pendulum rahisi hufafanuliwa kuwa na molekuli ya uhakika, pia inajulikana kama bob ya pendulum, ambayo imesimamishwa kutoka kamba ya urefu L na molekuli kidogo (Kielelezo\(\PageIndex{1}\)). Hapa, nguvu pekee zinazofanya bob ni nguvu ya mvuto (yaani, uzito wa bob) na mvutano kutoka kwenye kamba. Masi ya kamba inadhaniwa kuwa duni ikilinganishwa na wingi wa bob.

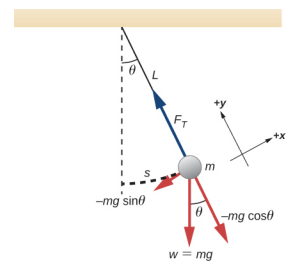
    Katika takwimu, bar ya usawa inavyoonyeshwa. Kamba ya urefu L inatoka kwenye bar kwa pembe theta kinyume chake kutoka wima. Mwelekeo wa wima unaonyeshwa na mstari uliopigwa unaotembea chini kutoka ambapo kamba imefungwa kwenye bar. Bob ya mviringo ya molekuli m inaunganishwa na mwisho wa kamba. Arc kutoka wingi kwa wima unahitajika kwa mstari mwingine dashed na ni urefu s. mshale nyekundu kuonyesha wakati T ya oscillation ya kundi inavyoonekana kwenye mstari kamba kuelekea bar. Mfumo wa kuratibu unaonyeshwa karibu na bob na mwelekeo mzuri wa y iliyokaa na kamba na kuelekeza kuelekea hatua ya egemeo na mwelekeo mzuri wa x unaoelezea tangent kwa arc na mbali na nafasi ya usawa. mshale bluu kutoka bob kuelekea egemeo, pamoja kamba, ni kinachoitwa F ndogo T. mshale nyekundu kutoka bob akizungumzia chini ni kinachoitwa w = m g. mshale nyekundu akizungumzia tangent kwa safu na kuelekea usawa, katika bala x mwelekeo, ni kinachoitwa bala m g sine theta. Mshale mweusi kwenye theta ya angle kinyume cha saa kutoka w ni kinachoitwa minus m g cosine theta.
    Kielelezo\(\PageIndex{1}\): Pendulum rahisi ina bob ndogo ya kipenyo na kamba ambayo ina molekuli ndogo sana lakini ina nguvu ya kutosha kunyoosha appreciably. Uhamisho wa mstari kutoka kwa usawa ni s, urefu wa arc. Pia inavyoonekana ni nguvu juu ya bob, ambayo husababisha nguvu wavu ya -mgsin\(\theta\) kuelekea nafasi ya usawa-yaani, nguvu ya kurejesha.

    Fikiria wakati juu ya pendulum. Nguvu ya kutoa wakati wa kurejesha ni sehemu ya uzito wa bob ya pendulum ambayo hufanya urefu wa arc. Wakati huo ni urefu wa kamba L mara sehemu ya nguvu ya wavu ambayo ni perpendicular kwa radius ya arc. Ishara ndogo inaonyesha vitendo vya wakati katika mwelekeo kinyume cha uhamisho wa angular:

    \[\begin{split} \tau & = -L (mg \sin \theta); \\ I \alpha & = -L (mg \sin \theta); \\ I \frac{d^{2} \theta}{dt^{2}} & = -L (mg \sin \theta); \\ mL^{2} \frac{d^{2} \theta}{dt^{2}} & = -L (mg \sin \theta); \\ \frac{d^{2} \theta}{dt^{2}} & = - \frac{g}{L} \sin \theta \ldotp \end{split}\]

    Suluhisho la equation hii tofauti inahusisha calculus ya juu, na ni zaidi ya upeo wa maandishi haya. Lakini kumbuka kuwa kwa pembe ndogo (chini ya 15°), dhambi\(\theta\) na\(\theta\) kutofautiana kwa chini ya 1%, hivyo tunaweza kutumia dhambi ndogo ya makadirio ya angle\(\theta\) ≈\(\theta\). Pembe\(\theta\) inaelezea nafasi ya pendulum. Kwa kutumia ndogo angle makadirio anatoa ufumbuzi takriban kwa pembe ndogo,

    \[\frac{d^{2} \theta}{dt^{2}} = - \frac{g}{L} \theta \ldotp \label{15.17}\]

    Kwa sababu equation hii ina fomu sawa na equation kwa SHM, ufumbuzi ni rahisi kupata. Mzunguko wa angular ni

    \[\omega = \sqrt{\frac{g}{L}} \label{15.18}\]

    na kipindi ni

    \[T = 2 \pi \sqrt{\frac{L}{g}} \ldotp \label{15.19}\]

    Kipindi cha pendulum rahisi hutegemea urefu wake na kuongeza kasi kutokana na mvuto. Kipindi hicho ni huru kabisa na mambo mengine, kama vile wingi na uhamisho wa juu. Kama ilivyo kwa oscillators rahisi ya harmonic, kipindi cha T kwa pendulum ni karibu huru ya amplitude, hasa ikiwa\(\theta\) ni chini ya 15°. Hata saa rahisi za pendulum zinaweza kubadilishwa vizuri na kubaki sahihi.

    Kumbuka utegemezi wa T juu ya g.Kama urefu wa pendulum unajulikana, inaweza kweli kutumika kupima kasi kutokana na mvuto, kama ilivyo katika mfano wafuatayo.

    Mfano\(\PageIndex{1}\): Measuring Acceleration due to Gravity by the Period of a Pendulum

    Je! Ni kasi gani kutokana na mvuto katika eneo ambako pendulum rahisi yenye urefu wa cm 75.000 ina kipindi cha 1.7357 s?

    Mkakati

    Tunaulizwa kupata g kutokana na kipindi cha T na urefu L wa pendulum. Tunaweza kutatua T = 2\(\pi\) L g kwa g, kuchukua tu kwamba angle ya kufuta ni chini ya 15°.

    Suluhisho
    1. Mraba T = 2\(\pi \sqrt{\frac{L}{g}}\) na kutatua kwa g: $$g = 4\ pi^ {2}\ frac {L} {T ^ {2}} ldotp$$
    2. Mbadala inayojulikana maadili katika equation mpya: $$g = 4\ pi^ {2}\ frac {0.75000\; m} {(1.7357\; s) ^ {2}}\ ldotp $$
    3. Tumia ili kupata g: $$g = 9.8281\; m/s^ {2}\ ldotp $$

    Umuhimu

    Njia hii ya kuamua g inaweza kuwa sahihi sana, ndiyo sababu urefu na kipindi hutolewa kwa tarakimu tano katika mfano huu. Kwa usahihi wa dhambi ya makadirio\(\theta\) ≈\(\theta\) kuwa bora kuliko usahihi wa urefu na kipindi cha pendulum, angle ya juu ya uhamisho inapaswa kuwekwa chini ya 0.5°.

    Zoezi\(\PageIndex{1}\)

    Mhandisi hujenga pendulums mbili rahisi. Wote wawili wamesimamishwa kutoka kwa waya ndogo zilizopatikana kwenye dari ya chumba. Kila pendulum hupanda 2 cm juu ya sakafu. Pendulum 1 ina bob yenye uzito wa kilo 10. Pendulum 2 ina bob yenye uzito wa kilo 100. Eleza jinsi mwendo wa pendulums utatofautiana ikiwa bobs zote mbili zimehamishwa kwa 12°.

    Pendulum ya kimwili

    Kitu chochote kinaweza kusonga kama pendulum. Fikiria mug ya kahawa kunyongwa kwenye ndoano katika pantry. Kama mug anapata knocked, oscillates nyuma na nje kama pendulum mpaka oscillations kufa nje. Tumeelezea pendulum rahisi kama molekuli ya uhakika na kamba. Pendulum ya kimwili ni kitu chochote ambacho oscillations yake ni sawa na yale ya pendulum rahisi, lakini haiwezi kuonyeshwa kama molekuli ya uhakika kwenye kamba, na usambazaji wa wingi lazima uingizwe katika usawa wa mwendo.

    Kwa ajili ya pendulum rahisi, nguvu ya kurejesha ya pendulum ya kimwili ni nguvu ya mvuto. Kwa pendulum rahisi, nguvu ya mvuto hufanya katikati ya bob ya pendulum. Katika kesi ya pendulum ya kimwili, nguvu ya mvuto hufanya katikati ya wingi (CM) ya kitu. kitu oscillates kuhusu uhakika O. Fikiria kitu cha sura generic kama inavyoonekana katika Kielelezo\(\PageIndex{2}\).

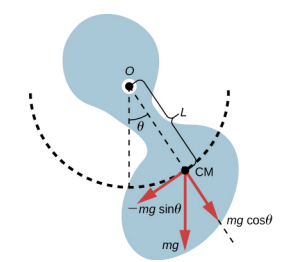
    Mchoro wa pendulum ya kimwili. Katika takwimu, pendulum ni kitu kisichokuwa na umbo. Katikati ya wingi, C M, ni umbali L kutoka hatua ya egemeo, O. katikati ya wingi huonyesha safu ya mviringo, unaozingatia O. mstari kutoka O hadi L hufanya angle theta kinyume cha wima. Majeshi matatu yanaonyeshwa na mishale nyekundu katikati ya wingi. Nguvu m g inaashiria chini. Vipengele vyake ni minus m g sine theta ambayo inaonyesha tangent kwa arc kufuatiliwa na katikati ya wingi, na m g cosine theta ambayo inaonyesha radially nje.
    Kielelezo\(\PageIndex{2}\): pendulum kimwili ni kitu chochote kwamba oscillates kama pendulum, lakini haiwezi inatokana kama molekuli uhakika juu ya kamba. Nguvu ya mvuto hufanya katikati ya wingi (CM) na hutoa nguvu ya kurejesha ambayo inasababisha kitu kufuta. Ishara ndogo juu ya sehemu ya uzito ambayo hutoa nguvu ya kurejesha iko kwa sababu nguvu hufanya kinyume cha angle inayoongezeka\(\theta\).

    Wakati pendulum ya kimwili iko kunyongwa kutoka hatua lakini ni huru kugeuka, inazunguka kwa sababu ya moment kutumika katika CM, zinazozalishwa na sehemu ya uzito wa kitu ambayo hufanya tangent kwa mwendo wa CM. Kuchukua mwelekeo kinyume na mwelekeo kuwa chanya, sehemu ya nguvu ya mvuto ambayo hufanya tangent kwa mwendo ni dhambi -mg\(\theta\). Ishara ndogo ni matokeo ya nguvu ya kurejesha kutenda kinyume cha angle inayoongezeka. Kumbuka kwamba wakati huo ni sawa na\(\vec{\tau} = \vec{r} \times \vec{F}\). Ukubwa wa wakati huo ni sawa na urefu wa mkono wa radius mara sehemu ya tangential ya nguvu inayotumiwa, |\(\tau\) | = RFSin\(\theta\). Hapa, urefu L wa mkono wa radius ni umbali kati ya hatua ya mzunguko na CM. Ili kuchambua mwendo, kuanza na wakati wa wavu. Kama pendulum rahisi, fikiria pembe ndogo tu ili dhambi\(\theta\) ≈\(\theta\). Kumbuka kutoka Fast-Axis mzunguko juu ya mzunguko kwamba moment wavu ni sawa na wakati wa hali I =\(\int\) r 2 dm mara kasi angular\(\alpha\), ambapo\ (\ alpha =\ frac {d ^ {2}\ theta} {dt^ {2}} {dt^ {2}}:

    \[I \alpha = \tau_{net} = L (-mg) \sin \theta \ldotp\]

    Kwa kutumia ndogo angle makadirio na upya upya:

    \[\begin{split} I \alpha & = -L (mg) \theta; \\ I \frac{d^{2} \theta}{dt^{2}} & = -L (mg) \theta; \\ \frac{d^{2} \theta}{dt^{2}} & = - \left(\dfrac{mgL}{I}\right) \theta \ldotp \end{split}\]

    Mara nyingine tena, equation inasema kuwa mara ya pili derivative ya nafasi (katika kesi hii, angle) ni sawa na minus\(\left(− \dfrac{mgL}{I}\right)\) mara kwa mara nafasi. Suluhisho ni

    \[\theta (t) = \Theta \cos (\omega t + \phi),\]

    \(\Theta\)wapi makazi ya angular ya juu. Mzunguko wa angular ni

    \[\omega = \sqrt{\frac{mgL}{I}} \ldotp \label{15.20}\]

    Kwa hiyo ni kipindi

    \[T = 2 \pi \sqrt{\frac{I}{mgL}} \ldotp \label{15.21}\]

    Kumbuka kuwa kwa pendulum rahisi, wakati wa inertia ni I =\(\int\) r 2 dm = mL 2 na kipindi kinapungua kwa T = 2\(\pi \sqrt{\frac{L}{g}}\).

    Mfano\(\PageIndex{2}\): Reducing the Swaying of a Skyscraper

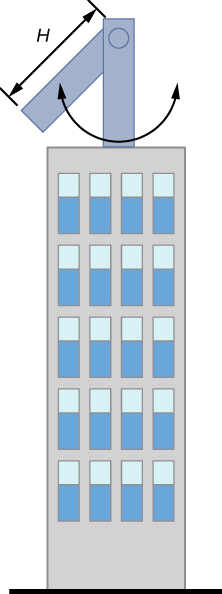
    Katika hali mbaya, skyscrapers wanaweza kutembea hadi mita mbili na mzunguko wa hadi 20.00 Hz kutokana na upepo mkali au shughuli za seismic. Makampuni kadhaa yameanzisha pendulums ya kimwili ambayo imewekwa juu ya skyscrapers. Kama skyscraper inakwenda kulia, pendulum inakuja upande wa kushoto, kupunguza njia. Kwa kuzingatia oscillations na mzunguko wa 0.50 Hz, kubuni pendulum ambayo ina boriti ndefu, wiani mara kwa mara, na wingi wa tani 100 za metri na pivot uhakika katika mwisho mmoja wa boriti. Je, urefu wa boriti unapaswa kuwa nini?

    Takwimu inaonyesha jengo refu na safu juu ya paa lake na fimbo ndefu ya urefu H ambayo inakuja kwenye hatua ya pivot karibu na juu ya safu.

    Mkakati

    Tunaulizwa kupata urefu wa pendulum ya kimwili na molekuli inayojulikana. Sisi kwanza tunahitaji kupata wakati wa inertia ya boriti. Tunaweza kisha kutumia equation kwa kipindi cha pendulum kimwili kupata urefu.

    Suluhisho
    1. Pata wakati wa inertia kwa CM.
    2. Tumia theorem ya mhimili sambamba ili kupata wakati wa hali kuhusu hatua ya mzunguko: $$I = I_ {CM} +\ Frac {L^ {2}} {4} M =\ frac {1} {12} ML^ {2} +\ frac {1} {4} ML^ {2} ML^ {2}\ ldotp$
    3. Kipindi cha pendulum ya kimwili kina kipindi cha T = 2\(\pi \sqrt{\frac{I}{mgL}}\). Tumia wakati wa hali ya kutatua kwa urefu L: $$\ kuanza {mgawanyiko} T & = 2\ pi\ sqrt {\ frac {I} {MgL}} = 2\ pi\ sqrt {\ frac {\ frac {1} {3} ML^ {2}} {MgL}} = 2\ pi\ sqrt {\ Frac {L} {3g}};\\ L & = 3g\ kushoto (\ dfrac {T} {2\ pi}\ haki) ^ {2} = 3 (9.8\; m/s^ {2})\ kushoto (\ dfrac {2\; s} {2\ pi}\ haki) ^ {2} = 2.98\; m\ ldotp\ mwisho { mgawanyiko} $$
    4. Urefu huu L unatoka katikati ya wingi hadi mhimili wa mzunguko, ambayo ni nusu ya urefu wa pendulum. Kwa hiyo urefu H wa pendulum ni: $$ H = 2L = 5.96\: m $$

    Umuhimu

    Kuna njia nyingi za kupunguza oscillations, ikiwa ni pamoja na kurekebisha sura ya skyscrapers, kwa kutumia pendulums nyingi za kimwili, na kutumia dampers zilizopangwa.

    Pendulum ya Torsional

    Pendulum ya torsional ina mwili mgumu uliosimamishwa na waya wa mwanga au spring (Kielelezo\(\PageIndex{3}\)). Wakati mwili unapotoshwa angle ndogo ya kiwango cha juu (\(\Theta\)) na kutolewa kutoka kwa kupumzika, mwili hutembea kati ya (\(\theta\)= +\(\Theta\)) na (\(\theta\)= ∙\(\Theta\)). Wakati wa kurejesha hutolewa na ufugaji wa kamba au waya.

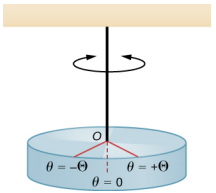
    Pendulum ya torsional inaonyeshwa katika takwimu hii. Pendulum ina disk ya usawa ambayo hutegemea kamba kutoka dari. Kamba inaunganisha disk katika kituo chake, katika hatua O. disk na kamba inaweza oscillate katika ndege usawa kati ya pembe pamoja Theta na minus Theta. Msimamo wa usawa ni kati ya hizi, saa theta = 0.
    Kielelezo\(\PageIndex{3}\): Pendulum ya torsional ina mwili mgumu uliosimamishwa na kamba au waya. Mwili mgumu hutenganisha kati ya (\(\theta\)= +\(\Theta\)) na (\(\theta\)= -\(\Theta\)).

    Wakati wa kurejesha unaweza kuonyeshwa kama kuwa sawa na angle:

    \[\tau = - \kappa \theta \ldotp\]

    Kappa ya kutofautiana (\(\kappa\)) inajulikana kama mara kwa mara ya msokoto wa waya au kamba. Ishara ndogo inaonyesha kwamba wakati wa kurejesha hufanya kinyume chake na kuongeza uhamisho wa angular. Wakati wa wavu ni sawa na wakati wa inertia mara kasi ya angular:

    \[\begin{split} I \frac{d^{2} \theta}{dt^{2}} & = - \kappa \theta; \\ \frac{d^{2} \theta}{dt^{2}} & = - \frac{\kappa}{I} \theta \ldotp \end{split}\]

    Equation hii inasema kuwa mara ya pili derivative ya nafasi (katika kesi hii, angle) sawa mara hasi mara kwa mara nafasi. Hii inaonekana sawa na equation ya mwendo kwa SHM\(\frac{d^{2} x}{dt^{2}}\) =\(\frac{k}{m}\) ∙ x, ambapo kipindi kilipatikana kuwa T = 2\(\pi \sqrt{\frac{m}{k}}\). Kwa hiyo, kipindi cha pendulum ya torsional kinaweza kupatikana kwa kutumia

    \[T = 2 \pi \sqrt{\frac{I}{\kappa}} \ldotp \label{15.22}\]

    Vitengo vya mara kwa mara ya torsion ni [\(\kappa\)] = N • m = (kg • m/s 2) m = kg • m 2 /s 2 na vitengo kwa wakati wa inertial ni [I] = kg • m 2, ambayo inaonyesha kuwa kitengo cha kipindi ni cha pili.

    Mfano\(\PageIndex{3}\): Measuring the Torsion Constant of a String

    Fimbo ina urefu wa l = 0.30 m na uzito wa kilo 4.00. Kamba inaunganishwa na CM ya fimbo na mfumo umefungwa kutoka dari (Kielelezo\(\PageIndex{4}\)). Fimbo imehamishwa 10° kutoka msimamo wa usawa na kutolewa kutoka kupumzika. Fimbo oscillates na kipindi cha 0.5 s. torsion mara kwa mara ni nini\(\kappa\)?

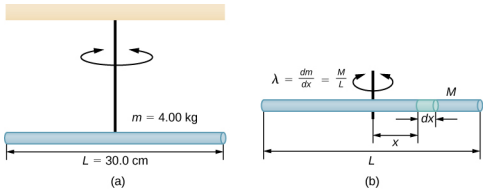
    Kielelezo a inaonyesha fimbo ya usawa, urefu wa sentimita 30.0 na uzito wa kilo 4.00, kunyongwa na kamba kutoka dari. Kamba inaunganisha katikati ya fimbo. Fimbo inazunguka na kamba katika ndege isiyo na usawa. Kielelezo b kinaonyesha fimbo na maelezo yanayohitajika ili kupata wakati wake wa inertia. Urefu wa fimbo, mwisho hadi mwisho, ni L na molekuli yake ya jumla ni M. ina linear wingi wiani lambda sawa d m d x ambayo pia sawa M juu L. sehemu ndogo ya fimbo ambayo ina urefu d x katika umbali x kutoka katikati ya fimbo ni yalionyesha. Kamba inaunganishwa na fimbo katikati ya fimbo.
    Kielelezo\(\PageIndex{4}\) - (a) Fimbo imesimamishwa na kamba kutoka dari. (b) Kupata wakati wa fimbo ya inertia.

    Mkakati

    Tunaulizwa kupata mara kwa mara ya torsion ya kamba. Sisi kwanza tunahitaji kupata wakati wa inertia.

    Suluhisho
    1. Pata muda wa inertia kwa CM: $$I_ {CM} =\ int x^ {2} dm =\ int_ {-\ frac {L} {2}} ^ {+\ frac {L} {2}} x ^ {2}\ lambda dx =\ lambda\ Bigg [\ frac {x^ {3}\ Bigg] _ {3}\ Bigg] _ {-\ frac {L} {2}} ^ {+\ FRAC {L} {2}} =\ lambda\ Frac {2L^ {3}} {24} =\ kushoto (\ dfrac {M} {L}\ haki)\ frac {2L^ {3}} {24} =\ frac {1} {12} ML^ {2}\ ldotp$$
    2. Tumia mara kwa mara ya msokoto kwa kutumia equation kwa kipindi: $$\ kuanza {split} T & = 2\ pi\ sqrt {\ Frac {I} {\ kappa}};\\ Kappa & = I\ kushoto (\ dfrac {2\ pi} {T}\ haki) ^ {2} =\ kushoto (\ dfrac {1} {12} ML^ {2} haki)\ kushoto (\ dfrac {2\ pi} {T}\ haki) ^ {2};\\ & =\ Big [\ frac {1} {12} (4.00\; kilo) (0.30\; m) ^ {2}\ Big]\ kushoto (\ dfrac {2\ pi} {0.50\; s}\ haki) ^ {2} = 4.73\; N\;\ cdotp m\ ldotp\ mwisho {mgawanyiko} $$

    Umuhimu

    Kama nguvu ya mara kwa mara ya mfumo wa kuzuia na spring, kubwa ya mara kwa mara ya torsion, mfupi kipindi.