14.8: Ulinganisho wa Bernoulli

Malengo ya kujifunza

• Eleza maneno katika equation ya Bernoulli
• Eleza jinsi equation ya Bernoulli inahusiana na uhifadhi wa nishati
• Eleza jinsi ya kupata kanuni ya Bernoulli kutoka kwa usawa wa Bernoulli
• Fanya mahesabu kwa kutumia kanuni ya Bernoulli
• Eleza baadhi ya matumizi ya kanuni ya Bernoulli

Kama tulivyoonyesha kwenye Mchoro 14.7.4, wakati maji yanaingia kwenye kituo kidogo, kasi yake huongezeka. Hiyo ina maana nishati yake ya kinetic pia huongezeka. Nishati ya kinetic iliyoongezeka inatokana na kazi ya wavu iliyofanywa kwenye maji ili kuiingiza kwenye kituo. Pia, ikiwa maji yanabadilika msimamo wa wima, kazi imefanywa kwenye maji kwa nguvu ya mvuto.

Tofauti ya shinikizo hutokea wakati kituo kinapungua. Tofauti hii shinikizo husababisha nguvu wavu juu ya maji kwa sababu shinikizo mara eneo sawa na nguvu, na nguvu hii wavu haina kazi. Kumbuka theorem ya kazi ya nishati,

\[W_{net} = \frac{1}{2} mv^{2} - \frac{1}{2} mv_{0}^{2} \ldotp\]

Kazi ya wavu imefanywa huongeza nishati ya kinetic ya maji. Matokeo yake, shinikizo hupungua kwa maji ya kusonga kwa haraka ikiwa maji yanafungwa kwenye tube.

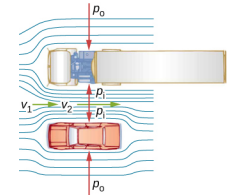
Kuna mifano mingi ya kawaida ya kushuka kwa shinikizo katika maji ya kusonga kwa kasi. Kwa mfano, mapazia ya kuogelea yana tabia isiyokubalika ya kuingia ndani ya duka la kuoga wakati oga iko. Sababu ni kwamba mkondo wa kasi wa maji na hewa hujenga eneo la shinikizo la chini ndani ya kuoga, wakati shinikizo upande mwingine unabaki katika shinikizo la kawaida la anga. Tofauti hii ya shinikizo husababisha nguvu ya wavu, kusuiza pazia ndani. Vile vile, wakati gari linapopita lori kwenye barabara kuu, magari hayo mawili yanaonekana kuelekea kila mmoja. Sababu ni sawa: Kasi ya hewa kati ya gari na lori inajenga eneo la shinikizo la chini kati ya magari, na huingizwa pamoja na shinikizo kubwa nje (Kielelezo\(\PageIndex{1}\)). Athari hii ilikuwa aliona mbali nyuma kama katikati ya miaka ya 1800, wakati ilibainika kuwa treni kupita katika pande kinyume tipped precariously kuelekea mtu mwingine.

Kielelezo\(\PageIndex{1}\): Mtazamo wa juu wa gari linalopita lori kwenye barabara kuu. Air kupita kati ya magari inapita katika kituo nyembamba na lazima kuongeza kasi yake (v2 ni kubwa kuliko v1), na kusababisha shinikizo kati yao kushuka (pi ni chini ya po). Shinikizo kubwa kwa nje linasubu gari na lori pamoja.

Hifadhi ya Nishati na Equation ya Bernoulli

Matumizi ya kanuni ya uhifadhi wa nishati kwa mtiririko wa laminar usio na msuguano husababisha uhusiano muhimu sana kati ya shinikizo na kasi ya mtiririko katika maji. Uhusiano huu unaitwa equation ya Bernoulli, iliyoitwa baada ya Daniel Bernoulli (1700—1782), aliyechapisha masomo yake juu ya mwendo wa maji katika kitabu chake Hydrodynamica (1738).

Fikiria maji yasiyotumiwa yanayotembea kupitia bomba ambayo ina kipenyo na urefu tofauti, kama inavyoonekana kwenye Mchoro\(\PageIndex{2}\). Subscripts 1 na 2 katika takwimu zinaashiria maeneo mawili kando ya bomba na kuonyesha uhusiano kati ya maeneo ya sehemu za msalaba A, kasi ya mtiririko v, urefu kutoka chini y, na shinikizo p kila hatua. Tunadhani hapa kwamba wiani katika pointi mbili ni sawa-kwa hiyo, wiani ni ulionyehsa na\(\rho\) bila michango yoyote-na tangu maji katika incompressible, kiasi kivuli lazima kuwa sawa.

Kielelezo\(\PageIndex{2}\): jiometri kutumika kwa ajili ya derivation ya equation Bernoulli ya.

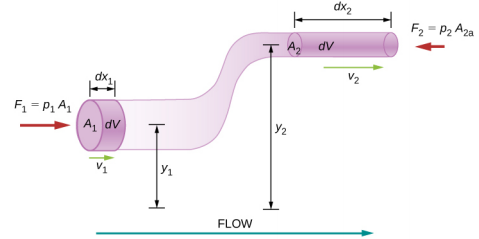
Tunadhani pia kuwa hakuna nguvu za viscous katika maji, hivyo nishati ya sehemu yoyote ya maji itahifadhiwa. Ili kupata equation ya Bernoulli, sisi kwanza tunahesabu kazi iliyofanyika kwenye maji:

\[\begin{split} dW & = F_{1} dx_{1} - F_{2} dx_{2} \\ & = p_{1} A_{1} dx_{1} - p_{2} A_{2} dx_{2} \\ & = p_{1} dV - p_{2} dV = (p_{1} - p_{2}) dV \ldotp \end{split}\]

Kazi iliyofanywa ilikuwa kutokana na nguvu ya kihafidhina ya mvuto na mabadiliko katika nishati ya kinetic ya maji. Mabadiliko katika nishati ya kinetic ya maji ni sawa na

\[dK = \frac{1}{2} m_{2} v_{2}^{2} - \frac{1}{2} m_{1} v_{1}^{2} = \frac{1}{2} \rho dV (v_{2}^{2} - v_{1}^{2}) \ldotp\]

Mabadiliko katika nishati ya uwezo ni

\[dU = mgy_{2} - mgy_{1} = \rho dV g(y_{2} - y_{1}) \ldotp\]

Equation nishati kisha inakuwa

\[\begin{split} dW & = dK + dU \\ (p_{1} - p_{2}) dV & = \frac{1}{2} \rho dV (v_{2}^{2} - v_{1}^{2}) + \rho dV g(y_{2} - y_{1}) \\ (p_{1} - p_{2}) & = \frac{1}{2} \rho (v_{2}^{2} - v_{1}^{2}) + \rho g(y_{2} - y_{1}) \ldotp \end{split}\]

Kupanga upya equation inatoa equation Bernoulli ya:

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho gy_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} + \rho gy_{2} \ldotp\]

Uhusiano huu unasema kwamba nishati ya mitambo ya sehemu yoyote ya mabadiliko ya maji kama matokeo ya kazi iliyofanywa na maji ya nje kwa sehemu hiyo, kutokana na shinikizo tofauti njiani. Kwa kuwa pointi hizo mbili zilichaguliwa kiholela, tunaweza kuandika equation ya Bernoulli kwa ujumla kama kanuni ya uhifadhi kando ya mtiririko.

Mlinganyo wa Bernoulli

Kwa maji yasiyo na msuguano, mchanganyiko wa shinikizo na jumla ya densities ya kinetic na uwezo wa nishati ni mara kwa mara si tu kwa muda, lakini pia pamoja na kuboresha:

\[p + \frac{1}{2} \rho v^{2} + \rho gy = constant \label{14.16}\]

Maelezo maalum yanapaswa kufanywa hapa ya ukweli kwamba katika hali ya nguvu, shinikizo la urefu sawa katika sehemu tofauti za maji inaweza kuwa tofauti ikiwa zina kasi tofauti za mtiririko.

Kuchambua Equation ya Bernoulli

Kulingana na equation ya Bernoulli, ikiwa tunafuata kiasi kidogo cha maji kando ya njia yake, kiasi mbalimbali kwa jumla kinaweza kubadilika, lakini jumla inabaki mara kwa mara. Equation ya Bernoulli ni, kwa kweli, taarifa rahisi ya uhifadhi wa nishati kwa maji yasiyoweza kuingizwa kwa kutokuwepo kwa msuguano.

Aina ya jumla ya equation ya Bernoulli ina maneno matatu ndani yake, na inatumika kwa upana. Ili kuelewa vizuri, hebu tuchunguze hali fulani ambazo zinawezesha na kuonyesha matumizi yake na maana yake.

Equation ya Bernoulli kwa maji ya tuli

Kwanza fikiria hali rahisi sana ambapo maji ni tuli-yaani,\(v_1 = v_2 = 0\). Equation Bernoulli katika kesi hiyo ni

\[p_{1} + \rho gh_{1} = p_{2} + \rho gh_{2} \ldotp\]

Tunaweza zaidi kurahisisha equation kwa kuweka h ₂ = 0. (Urefu wowote unaweza kuchaguliwa kwa urefu wa kumbukumbu ya sifuri, kama mara nyingi hufanyika kwa hali nyingine zinazohusisha nguvu ya mvuto, na kufanya urefu mwingine wote jamaa.) Katika kesi hii, tunapata

\[p_{2} = p_{1} + \rho gh_{1} \ldotp\]

Equation hii inatuambia kwamba, katika maji ya tuli, shinikizo huongezeka kwa kina. Tunapoenda kutoka hatua ya 1 hadi kumweka 2 katika maji, kina kinaongezeka kwa h ₁, na kwa hiyo, p ₂ ni kubwa kuliko p ₁ kwa kiasi\(\rho gh_1\). Katika kesi rahisi sana, p ₁ ni sifuri juu ya maji, na tunapata uhusiano wa kawaida\(p = \rho gh\). (Kumbuka kwamba p =\(\rho gh\) na\(\Delta Ug = −mgh\).) Hivyo, equation ya Bernoulli inathibitisha ukweli kwamba mabadiliko ya shinikizo kutokana na uzito wa maji ni\(\rho gh\). Ingawa tunaanzisha equation ya Bernoulli kwa mwendo wa maji, inajumuisha mengi ya yale tuliyojifunza kwa maji ya tuli mapema.

Kanuni ya Bernoulli

Tuseme maji yanasogea lakini kina chake ni mara kwa mara—yaani\(h_1 = h_2\). Chini ya hali hii, equation ya Bernoulli inakuwa

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} = p_{2} + \frac{1}{2} \rho v_{2}^{2} \ldotp \label{Bernoulli}\]

Hali ambazo maji hutiririka kwa kina cha mara kwa mara ni ya kawaida sana kwamba equation hii mara nyingi huitwa pia kanuni ya Bernoulli, ambayo ni equation tu ya Bernoulli kwa maji kwa kina cha mara kwa mara. (Kumbuka tena kwamba hii inatumika kwa kiasi kidogo cha maji tunapofuata kwenye njia yake.) Kanuni ya Bernoulli inaimarisha ukweli kwamba shinikizo hupungua kama kasi inavyoongezeka katika maji ya kusonga: Ikiwa v ₂ ni kubwa kuliko v ₁ katika equation, basi p ₂ lazima iwe chini ya p ₁ kwa usawa wa kushikilia.

Mfano 14.6: Kuhesabu Shinikizo

Katika Mfano 14.5, tumegundua kwamba kasi ya maji katika hose iliongezeka kutoka 1.96 m/s hadi 25.5 m/s kutoka hose hadi bomba. Tumia shinikizo katika hose, kutokana na kwamba shinikizo kamili katika bomba ni 1.01 x 10 ⁵ N/m ² (anga, kama ni lazima) na kuchukua kiwango, mtiririko usio na msuguano.

Mkakati

Mtiririko wa kiwango unamaanisha kina kirefu, hivyo kanuni ya Bernoulli inatumika. Tunatumia usajili 1 kwa maadili katika hose na 2 kwa wale walio katika bomba. Sisi ni hivyo aliuliza kupata p ₁.

Suluhisho

Kutatua kanuni ya Bernoulli (Equation Bernoulli) kwa ajili ya\(p_1\) mavuno

\[ \begin{align*} p_{1} &= p_{2} \frac{1}{2} \rho v_{2}^{2} - \frac{1}{2} \rho v_{1}^{2} \\[4pt] &= p_{2} + \frac{1}{2} \rho (v_{2}^{2} - v_{1}^{2}) \ldotp \end{align*}\]

Kubadilisha maadili inayojulikana,

\[\begin{align*} p_{1} & = (1.01 \times 10^{5}\; N/m^{2}) + \frac{1}{2} (10^{3}\; kg/m^{3})[(25.5\; m/s)^{2} - (1.96\; m/s)^{2}] \\[4pt] & = 4.24 \times 10^{5}\; N/m^{2} \ldotp \end{align*}\]

Umuhimu

Shinikizo hili kabisa katika hose ni kubwa zaidi kuliko pua, kama inavyotarajiwa, tangu v ni kubwa zaidi katika bomba. Shinikizo p ₂ katika bomba lazima iwe anga, kwa sababu maji hujitokeza ndani ya anga bila mabadiliko mengine katika hali.

Matumizi ya Kanuni ya Bernoulli

Vifaa na hali nyingi hutokea ambapo maji hutembea kwa urefu wa mara kwa mara na hivyo inaweza kuchambuliwa na kanuni ya Bernoulli.

Kuingilia

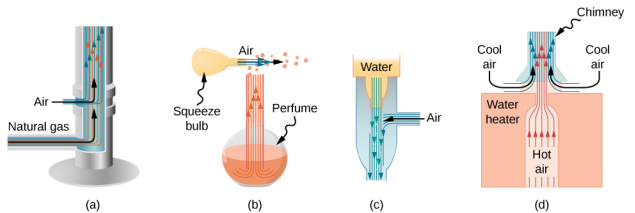
Kwa muda mrefu watu wameweka kanuni ya Bernoulli kufanya kazi kwa kutumia shinikizo lililopunguzwa katika maji ya juu ya kasi ili kusonga mambo. Kwa shinikizo la juu kwa nje, maji ya juu-kasi husababisha maji mengine ndani ya mkondo. Utaratibu huu unaitwa entrainment. Vifaa vya kuingizwa vimekuwa vinatumika tangu nyakati za kale kama pampu za kuongeza maji kwa urefu mdogo, kama ni muhimu kwa kukimbia mabwawa, mashamba, au maeneo mengine ya chini. Vifaa vingine vinavyotumia dhana ya kuingizwa vinaonyeshwa kwenye Kielelezo\(\PageIndex{3}\).

Kielelezo\(\PageIndex{3}\): Vifaa vya kuingizwa hutumia kasi ya maji ili kuunda shinikizo la chini, ambalo linaingiza maji moja hadi nyingine. (a) Burner ya Bunsen hutumia pua ya gesi inayoweza kubadilishwa, kuingiza hewa kwa mwako sahihi. (b) Atomizer hutumia bulb itapunguza kuunda ndege ya hewa inayoingiza matone ya manukato. Sprayers ya rangi na carburetors hutumia mbinu zinazofanana sana ili kusonga maji yao. (c) Aspirator ya kawaida hutumia mkondo wa maji yenye kasi ili kujenga eneo la shinikizo la chini. Aspirators inaweza kutumika kama pampu suction katika hali ya meno na upasuaji au kwa ajili ya kukimbia basement mafuriko au kuzalisha shinikizo kupunguzwa katika chombo. (d) Chimney cha joto la maji kimeundwa kuingiza hewa ndani ya bomba inayoongoza kupitia dari.

Upimaji wa kasi

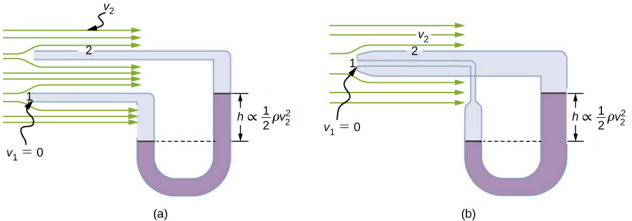
Kielelezo\(\PageIndex{4}\) kinaonyesha vifaa viwili vinavyotumia kanuni ya Bernoulli kupima kasi ya maji. Manometer katika sehemu (a) imeshikamana na zilizopo mbili ambazo ni ndogo kutosha kusisumbua mtiririko. Bomba linalokabiliwa na maji linalojitokeza linajenga doa lililokufa likiwa na kasi ya sifuri (v ₁ = 0) mbele yake, wakati maji ya kupita tube nyingine ina kasi v ₂. Hii ina maana kwamba kanuni Bernoulli kama ilivyoelezwa katika

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} = p_{2} + \frac{1}{2} \rho v_{2}^{2}\]

inakuwa

\[p_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} \ldotp\]

Hivyo shinikizo p ₂ juu ya ufunguzi wa pili ni kupunguzwa na\(\frac{1}{2} \rho v_{2}^{2}\), hivyo maji katika manometer kuongezeka kwa h upande kushikamana na ufunguzi wa pili, ambapo

\[h \propto \frac{1}{2} \rho v_{2}^{2} \ldotp\]

(Kumbuka kwamba ishara\(\propto\) ina maana “sawia na.”) Kutatua kwa v ₂, tunaona kwamba

\[v_{2} \propto \sqrt{h} \ldotp\]

Sehemu (b) inaonyesha toleo la kifaa hiki ambacho ni katika matumizi ya kawaida kwa kupima kasi mbalimbali za maji; vifaa vile hutumika mara nyingi kama viashiria vya kasi ya hewa katika ndege.

Kielelezo\(\PageIndex{4}\): Upimaji wa kasi ya maji kulingana na kanuni ya Bernoulli. (a) Manometer imeshikamana na zilizopo mbili zilizo karibu na ndogo za kutosha kuvuruga mtiririko. Tube 1 inafunguliwa mwishoni inakabiliwa na mtiririko. Doa iliyokufa yenye kasi ya sifuri imeundwa huko. Tube 2 ina ufunguzi upande, hivyo maji ina kasi v katika ufunguzi; hivyo, shinikizo kuna matone. Tofauti katika shinikizo kwenye manometer ni\(\frac{1}{2} \rho v_{2}^{2}\), hivyo h ni sawa na\(\frac{1}{2} \rho v_{2}^{2}\). (b) Aina hii ya kifaa cha kupima kasi ni tube ya Prandtl, pia inajulikana kama tube ya pitot.

Hose ya moto

Matumizi yote yaliyotangulia ya equation ya Bernoulli yalihusisha hali ya kurahisisha, kama vile urefu wa mara kwa mara au shinikizo la mara kwa mara. Mfano unaofuata ni matumizi ya jumla zaidi ya equation ya Bernoulli ambayo shinikizo, kasi, na urefu wote hubadilika.

Mfano 14.7: Kuhesabu Shinikizo - Bomba la Moto la Moto

Hoses za moto zinazotumiwa katika moto mkubwa wa miundo zina kipenyo cha ndani cha cm 6.40 (Kielelezo\(\PageIndex{5}\)). Tuseme hose hiyo hubeba mtiririko wa 40.0 L/s, kuanzia shinikizo la kupima la 1.62 x 10 ⁶ N/m ². Ya hose huongezeka hadi 10.0 m kando ya ngazi hadi bomba iliyo na kipenyo cha ndani cha cm 3.00. Je! Shinikizo ni nini katika bomba?

Kielelezo\(\PageIndex{5}\): Shinikizo katika bomba la hose hii ya moto ni chini ya kiwango cha chini kwa sababu mbili: Maji yanapaswa kwenda kupanda ili kufikia bomba, na kasi huongezeka kwa bubu. Licha ya shinikizo lake la kupungua, maji yanaweza kutumia nguvu kubwa juu ya chochote kinachopiga kwa sababu ya nishati yake ya kinetic. Shinikizo katika mkondo wa maji huwa sawa na shinikizo la angahewa mara inapojitokeza hewani.

Mkakati

Tunapaswa kutumia equation ya Bernoulli kutatua kwa shinikizo, kwani kina si mara kwa mara.

Suluhisho

Equation ya Bernoulli ni

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho gh_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} + \rho gh_{2} \nonumber \]

ambapo usajili 1 na 2 hutaja hali ya awali kwenye ngazi ya chini na hali ya mwisho ndani ya bomba, kwa mtiririko huo. Ni lazima kwanza kupata kasi v ₁ na v ₂. Tangu Q = A ₁ v ₁, tunapata

\[v_{1} = \frac{Q}{A_{1}} = \frac{40.0 \times 10^{-3}\; m^{3}/s}{\pi (3.20 \times 10^{-2}\; m)^{2}} = 12.4\; m/s \ldotp \nonumber\]

Vile vile, tunaona

\[v_{2} = 56.6\; m/s \ldotp \nonumber\]

Hii kasi kubwa ni muhimu katika kufikia moto. Sasa, kuchukua h ₁ kuwa sifuri, sisi kutatua equation Bernoulli kwa p ₂:

\[p_{2} = p_{1} + \frac{1}{2} \rho (v_{1}^{2} - v_{2}^{2}) - \rho gh_{2} \ldotp \nonumber\]

Kubadilisha maadili inayojulikana mavuno

\[\begin{align*} p_{2} & = (1.62 \times 10^{6}\; N/m^{2}) + \frac{1}{2} (1000\; kg/m^{3}) [(12.4\; m/s)^{2} - (56.6\; m/s)^{2}] - (1000\; kg/m^{3})(9.80\; m/s^{2})(10.0\; m) \\ & = 0 \ldotp \end{align*}\]

Umuhimu

Thamani hii ni shinikizo la kupima, kwani shinikizo la awali lilipewa kama shinikizo la kupima. Hivyo, shinikizo la bomba linalingana na shinikizo la anga kama ni lazima, kwa sababu maji hutoka angahewa bila mabadiliko katika hali yake.