14.7: Dynamics ya maji

Last updated
Save as PDF

Page ID: 177034

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Eleza sifa za mtiririko
Tumia kiwango cha mtiririko
Eleza uhusiano kati ya kiwango cha mtiririko na kasi
Eleza matokeo ya equation ya mwendelezo wa uhifadhi wa molekuli

Sehemu ya kwanza ya sura hii ilihusika na statics ya maji, utafiti wa maji wakati wa kupumzika. Wengine wa sura hii inahusika na mienendo ya maji, utafiti wa maji katika mwendo. Hata aina ya msingi ya mwendo wa maji inaweza kuwa ngumu sana. Kwa sababu hii, tunapunguza uchunguzi wetu kwa maji bora katika mifano mingi. Maji bora ni maji yenye viscosity duni. Viscosity ni kipimo cha msuguano wa ndani katika maji; tunaiangalia kwa undani zaidi katika Viscosity na Turbulence. Katika mifano michache, sisi kuchunguza maji incompressible - moja ambayo nguvu kubwa sana inahitajika kubadili kiasi-tangu wiani katika maji incompressible ni mara kwa mara katika.

Tabia ya Flow

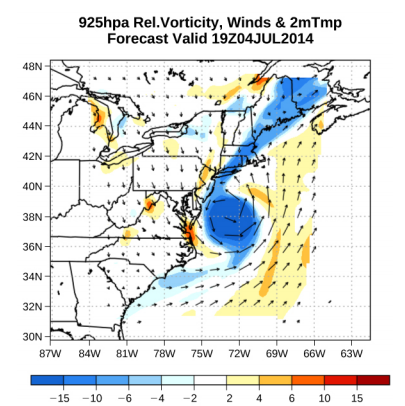
Vectors ya kasi mara nyingi hutumiwa kuonyesha mwendo wa maji katika programu kama hali ya hewa. Kwa mfano, upepo mwendo wa maji ya hewa katika angahira-unaweza kuwakilishwa na vectors kuonyesha kasi na mwelekeo wa upepo katika hatua yoyote fulani kwenye ramani. Kielelezo$\PageIndex{1}$ inaonyesha kasi wadudu kuelezea upepo wakati wa Hurricane Arthur katika 2014.

Kielelezo ni shinikizo ramani ya Hurricane Arthur kusafiri hadi Pwani ya Mashariki. Kituo cha shinikizo cha chini kinaonyeshwa kama dot ya bluu. Kasi ya upepo ni ya juu karibu na kituo cha shinikizo la chini na upepo unahamia mwelekeo wa kinyume chake. — Kielelezo$\PageIndex{1}$: Vectors kasi kuonyesha mtiririko wa upepo katika Hurricane Arthur. Angalia mzunguko wa upepo karibu na jicho la kimbunga. Kasi ya upepo ni ya juu karibu na jicho. Rangi huwakilisha vorticity ya jamaa, kipimo cha kugeuka au kugeuka kwa hewa.

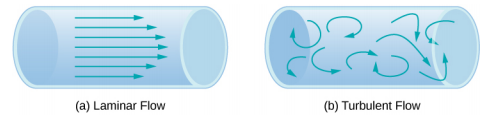
Njia nyingine ya kuwakilisha mwendo wa maji ni kuboresha. Kuboresha inawakilisha njia ya kiasi kidogo cha maji kama inapita. Kasi daima ni tangential kwa kuboresha. michoro katika Kielelezo$\PageIndex{2}$ kutumia streamlines kuonyesha mifano miwili ya maji ya kusonga kwa njia ya bomba. Maji ya kwanza yanaonyesha mtiririko wa laminar (wakati mwingine huelezewa kama mtiririko wa kutosha), unaowakilishwa na streamlines laini, sambamba. Kumbuka kuwa katika mfano umeonyeshwa katika sehemu (a), kasi ya maji ni kubwa zaidi katikati na hupungua karibu na kuta za bomba kutokana na mnato wa maji na msuguano kati ya kuta za bomba na maji. Hii ni kesi maalum ya mtiririko wa laminar, ambapo msuguano kati ya bomba na maji ni ya juu, inayojulikana kama hakuna hali ya mipaka ya kuingizwa. Mchoro wa pili unawakilisha mtiririko mkali, ambapo streamlines ni kawaida na hubadilika kwa muda. Katika mtiririko mkali, njia za mtiririko wa maji ni kawaida kama sehemu tofauti za maji huchanganya pamoja au huunda mikoa midogo ya mviringo inayofanana na whirlpools. Hii inaweza kutokea wakati kasi ya maji hufikia kasi fulani muhimu.

Kielelezo A ni schematic ya mtiririko laminar inavyoonekana kama tabaka ya maji kusonga katika mistari sambamba. Kielelezo B ni schematics ya mtiririko turbulent inavyoonekana kama tabaka ya maji kusonga katika njia isiyo ya kawaida, colliding. — Kielelezo$\PageIndex{2}$: (a) Mzunguko wa Laminar unaweza kufikiriwa kama tabaka za maji zinazohamia katika njia sawa, za kawaida. (b) Katika mtiririko mkali, mikoa ya maji huhamia katika njia isiyo ya kawaida, ya kupigana, na kusababisha kuchanganya na kugeuka.

Kiwango cha Mtiririko na Uhusiano wake na Velocity

Kiasi cha maji kinachopita kwa eneo lililopewa kupitia eneo wakati wa kipindi kinachoitwa kiwango cha mtiririko$Q$, au zaidi, kiwango cha mtiririko wa kiasi. Katika alama, hii imeandikwa kama

\[Q = \frac{dV}{dt} \label{14.13}\]

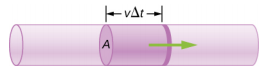
wapi$V$ kiasi na$t$ ni wakati uliopita. Katika Kielelezo$\PageIndex{3}$, kiasi cha silinda ni$Ax$, hivyo kiwango cha mtiririko ni

\[Q = \frac{dV}{dt} = \frac{d}{dt} (Ax) = A \frac{dx}{dt} = Av \ldotp\]

Kitengo cha SI cha kiwango cha mtiririko ni m ³ /s, lakini vitengo vingine kadhaa$Q$ vinatumiwa kwa kawaida, kama lita kwa dakika (L/min). Kumbuka kwamba lita (L) ni 1/1000 ya mita za ujazo au sentimita za ujazo 1000 (^{10 -3} m ³ au 10 ³ cm ³).

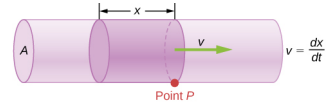
Kielelezo ni schematic ya bomba sare na sehemu ya msalaba A. fluid inapita kupitia bomba. Kiasi cha maji V hupita hatua P kwa wakati t. — Kielelezo$\PageIndex{3}$: Kiwango cha mtiririko ni kiasi cha maji yanayotembea nyuma ya hatua kupitia eneo$A$ kwa wakati wa kitengo. Hapa, silinda kivuli cha maji inapita hatua ya zamani$P$ katika bomba sare kwa wakati$t$.

Kiwango cha mtiririko na kasi ni kuhusiana, lakini tofauti kabisa, kiasi cha kimwili. Ili kufanya tofauti wazi, fikiria kiwango cha mtiririko wa mto. Kasi kubwa ya maji, kiwango kikubwa cha mtiririko wa mto. Lakini kiwango cha mtiririko pia hutegemea ukubwa na sura ya mto. Mkondo wa mlima wa haraka hubeba maji kidogo sana kuliko mto Amazon nchini Brazil, kwa mfano. Kielelezo$\PageIndex{3}$ unaeleza kiwango cha mtiririko wa kiasi. Kiwango cha mtiririko wa kiasi ni$Q = \frac{dV}{dt} = Av$, ambapo A ni sehemu ya msalaba wa bomba na v ni ukubwa wa kasi.

Uhusiano sahihi kati ya kiwango cha mtiririko$Q$ na kasi$v$ ya wastani ni

\[Q = Av,\]

$A$wapi eneo la msalaba na$v$ ni kasi ya wastani. Uhusiano inatuambia kwamba kiwango cha mtiririko ni sawia moja kwa moja na kasi ya wastani ya maji na eneo la msalaba wa mto, bomba, au mfereji mwingine. Kubwa cha mfereji, eneo kubwa zaidi la msalaba. Kielelezo$\PageIndex{3}$ unaeleza jinsi uhusiano huu ni kupatikana. Silinda ya kivuli ina kiasi$V = Ad$, ambacho kinapita nyuma ya hatua$P$ kwa wakati$t$. Kugawanya pande zote mbili za uhusiano huu kwa$t$ anatoa

\[\frac{V}{t} = \frac{Ad}{t} \ldotp \label{eq14.14A} \]

Tunaona kwamba$Q = \frac{V}{t}$ na kasi ya wastani ni$v = \frac{d}{t}$. Hivyo Equation\ ref {eq14.14a} inakuwa

\[Q = Av.\]

Kielelezo$\PageIndex{4}$ kinaonyesha maji yasiyotumiwa yanayotembea kwenye bomba la radius iliyopungua. Kwa sababu maji ni incompressible, kiasi hicho cha maji lazima kati yake kupita hatua yoyote katika tube katika muda fulani ili kuhakikisha mwendelezo wa mtiririko. Mtiririko unaendelea kwa sababu hawana vyanzo au kuzama vinavyoongeza au kuondoa wingi, hivyo umati unaoingia ndani ya bomba lazima uwe sawa na wingi unaotoka nje ya bomba. Katika kesi hiyo, kwa sababu eneo la msalaba wa bomba hupungua, kasi lazima iongeze. Mantiki hii inaweza kupanuliwa ili kusema kwamba kiwango cha mtiririko lazima iwe sawa katika pointi zote kwenye bomba. Hasa, kwa pointi holela 1 na 2,

\[\begin{split} Q_{1} & = Q_{2}, \\ A_{1} v_{1} & = A_{2} v_{2} \ldotp \end{split} \label{14.14}\]

Hii inaitwa equation ya kuendelea na halali kwa maji yoyote incompressible (na wiani mara kwa mara). Matokeo ya equation ya mwendelezo yanaweza kuzingatiwa wakati maji inapita kutoka hose ndani ya bomba nyembamba ya dawa: Inaibuka kwa kasi kubwa-hiyo ndiyo madhumuni ya bomba. Kinyume chake, wakati mto unapoingia kwenye mwisho mmoja wa hifadhi, maji hupungua kwa kiasi kikubwa, labda kuokota kasi tena inapoacha mwisho mwingine wa hifadhi. Kwa maneno mengine, kasi huongezeka wakati eneo la msalaba hupungua, na kasi hupungua wakati eneo la msalaba linaongezeka.

Kielelezo ni schematic ya bomba ambayo imepungua kutoka eneo la msalaba A1 hadi eneo la msalaba A2. Fluid inapita kupitia bomba. Kiasi cha maji V1 hupita hatua ya 1, iko kwenye sehemu kubwa ya msalaba, kwa wakati t Kiasi cha maji V2 hupita hatua ya 2, iko katika sehemu nyembamba ya msalaba, kwa wakati t. — Kielelezo$\PageIndex{4}$: Wakati tube inapungua, kiasi sawa kinachukua urefu mkubwa. Kwa kiasi sawa cha kupitisha pointi 1 na 2 kwa wakati fulani, kasi lazima iwe kubwa zaidi katika hatua ya 2. Mchakato huo unarekebishwa kabisa. Ikiwa maji yanapita katika mwelekeo kinyume, kasi yake inapungua wakati tube inapanuka. (Kumbuka kuwa kiasi cha jamaa cha mitungi miwili na mishale ya vector ya kasi ya sambamba haipatikani kwa kiwango.)

Kwa kuwa vinywaji ni kimsingi incompressible, equation ya kuendelea ni halali kwa vinywaji vyote. Hata hivyo, gesi ni compressible, hivyo equation lazima kutumika kwa tahadhari kwa gesi kama wao ni chini ya compression au upanuzi.

Mfano 14.5: Kuhesabu kasi ya maji kwa njia ya bomba

Bomba yenye kipenyo cha cm 0.500 inaunganishwa na hose ya bustani yenye radius ya cm 0.900. Kiwango cha mtiririko kupitia hose na bomba ni 0.500 L/s.

katika hose na
katika bomba.

Mkakati

Tunaweza kutumia uhusiano kati ya kiwango cha mtiririko na kasi ili kupata kasi zote mbili. Tunatumia usajili 1 kwa hose na 2 kwa bomba.

Suluhisho

Tunatatua usawa wa kiwango cha mtiririko kwa kasi na matumizi$\pi r_{1}^{2}$ kwa eneo la msalaba wa hose, kupata $$v =\ frac {Q} {A} =\ frac {Q} {\ pi r_ {1} ^ {2}}\ ldotp $$ Kubadilisha maadili na kutumia mabadiliko ya kitengo sahihi huzalisha $$v =\ frac {(0.500\; L/s) (10^ {-3}\ m; ^ {3} /L)} {(3.14) (9.00\ mara 10^ {-3}\; m) ^ {2} } = 1.96\; m/s\ ldotp $$
Tunaweza kurudia hesabu hii ili kupata kasi katika nozzle v ₂, lakini tunatumia equation ya mwendelezo kutoa ufahamu tofauti. Equation inasema $$A_ {1} v_ {1} = A_ {2} v_ {2}\ lDOTP$$Kutatua kwa v ₂ na kubadilisha$\pi r^{2}$ eneo la msalaba huzaa $$v_ {2} =\ frac {A_ {1}} {A_ {2}} v_ {1} =\ frac {\ pi r_ {1} ^ {2}} {2}} {pi r_ {2} ^ {2}} v_ {1} =\ frac {r_ {1} ^ {2}} {r_ {2} ^ {2}} v_ {1}\ ldotp $$ Kubadilisha maadili inayojulikana, $$v_ {2} =\ frac {(0.900\; cm) ^ {2}} {(0.250\; cm) ^ {2}} (1.96\; m/s) = 25.5\; m/s\ ldotp$$

Umuhimu

Kasi ya 1.96 m/s ni juu ya haki kwa maji yanayotokana na hose bila bomba. Bomba hutoa mkondo wa kasi sana tu kwa kuzuia mtiririko kwenye tube nyembamba.

Suluhisho la sehemu ya mwisho ya mfano inaonyesha kwamba kasi ni inversely sawia na mraba wa radius ya tube, na kufanya athari kubwa wakati radius inatofautiana. Tunaweza kupiga mshumaa kwa mbali kabisa, kwa mfano, kwa kunyoosha midomo yetu, wakati kupiga mshumaa kwa kinywa chetu wazi ni ufanisi kabisa.

Misa Hifadhi

Kiwango cha mtiririko wa maji pia kinaweza kuelezewa na kiwango cha mtiririko wa wingi au kiwango cha mtiririko wa mtiririko. Hii ni kiwango ambacho wingi wa maji hupita hatua. Rejea tena kwenye Kielelezo$\PageIndex{3}$, lakini wakati huu fikiria wingi katika kiasi kilichovuliwa. Uzito unaweza kuamua kutoka kwa wiani na kiasi:

\[m = \rho V = \rho Ax \ldotp\]

Kiwango cha mtiririko wa molekuli ni basi

\[\frac{dm}{dt} = \frac{d}{dt} (\rho Ax) = \rho A \frac{dx}{dt} = \rho Av,\]

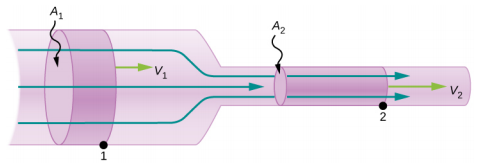
ambapo$\rho$ ni wiani, A ni eneo msalaba-Sectional, na v ni ukubwa wa kasi. Kiwango cha mtiririko wa wingi ni kiasi muhimu katika mienendo ya maji na inaweza kutumika kutatua matatizo mengi. Fikiria Kielelezo$\PageIndex{5}$. Bomba katika takwimu huanza kwenye pembe na sehemu ya msalaba wa A _{1 na inakabiliana} na bandari yenye sehemu ndogo ya msalaba wa A ₂. Masi ya maji ya kuingia kwenye bomba inapaswa kuwa sawa na wingi wa maji ya kuacha bomba. Kwa sababu hii kasi katika bandari (v ₂) ni kubwa kuliko kasi ya pembe (v ₁). Kwa kutumia ukweli kwamba wingi wa maji kuingia kwenye bomba lazima iwe sawa na wingi wa maji kutoka bomba, tunaweza kupata uhusiano kati ya kasi na eneo la msalaba kwa kuchukua kiwango cha mabadiliko ya wingi ndani na nje ya wingi:

\[\begin{split} \left(\dfrac{dm}{dt}\right)_{1} & = \left(\dfrac{dm}{dt}\right)_{2} \\ \rho_{1} A_{1} v_{1} & = \rho_{2} A_{2} v_{2} \ldotp \end{split} \label{14.15}\]

Equation\ ref {14.15} pia inajulikana kama equation mwendelezo kwa namna ya jumla. Ikiwa wiani wa maji hubakia mara kwa mara kwa njia ya kikwazo - yaani, maji hayajaingizwa-basi wiani hufuta kutoka kwa usawa wa kuendelea,

\[A_{1} v_{1} = A_{2} v_{2} \ldotp\]

Equation inapunguza kuonyesha kwamba kiwango cha mtiririko wa kiasi ndani ya bomba ni sawa na kiwango cha mtiririko wa kiasi nje ya bomba.

Kielelezo ni schematic ya maji yanayotembea katika bomba sare na sehemu ya msalaba eneo A. kiasi cha maji V delta t hupita bomba wakati delta t. — Kielelezo$\PageIndex{5}$: Jiometri kwa deriving equation ya mwendelezo. Kiasi cha kioevu kinachoingia katika eneo la msalaba (kivuli) lazima iwe sawa na kiasi cha kioevu kinachoacha eneo la msalaba ikiwa kioevu hakiwezi kupunguzwa.